Перевод Кантора И.А.
Подход 1


Будем рассматривать нашу задачу из системы координат с началом в центре первой окружности.
Определить центр окружности по каноническому уравнению вида Ax 2 + Ay 2 + a1x + a2y + a0 = 0, где A =/= 0, довольно просто — это (-a1/2A, -a2/2A);
перенести систему координат можно простым преобразованием
— подставить вместо старых переменных их новые значения в уравнения.
В такой системе координат уравнения окружностей можно записать как
(1) x 2 + y 2 = R 2 (2)(x-a) 2 + (y-b) 2 = r 2
Раскрывая скобки, вычитая (1) из (2) и приводя подобные, получаем другой вид (2):
-2ax-2by = R 2 — r 2 — a 2 — b 2 .
Если еще упростить и немного поменять обозначения, то (2) приведется к виду
ax+by=C, где С — новое обозначение выражения справа.
Таким образом, имеем систему:
(1) x 2 + y 2 = R 2 (2) ax + by = C,
решение которой, надеюсь, не составит проблем (например, подойдет подстановка — естественно с учетом случаев a=0, b=0 и т.п.) (2) в (1) и имеем простое квадратное уравнение на одну из переменных.
Решив его и получив из (2) значение оставшейся переменной, имеем(если и только если она есть) точку пересечения.
Подход 2


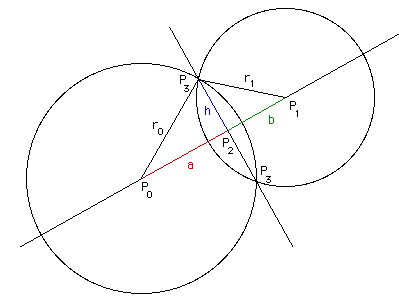
Пусть нужно найти пару точек P3 пересечения, если они существуют.
Для начала найдем расстояние между центрами окружностей. d = || P1 — P0 ||. Если d > r0 + r1, тогда решений нет: круги лежат отдельно. Аналогично в случае d a 2 + h 2 = r0 2 and b 2 + h 2 = r1 2
Используя равенство d = a + b, мы можем разрешить относительно a:
a = (r0 2 — r1 2 + d 2 ) / (2 d)
В случае соприкосновения окружностей, это, очевидно, превратится в r0, так как: d = r0 + r1
Решим относительно h, подставив в первое уравнение h 2 = r0 2 — a 2
Таким образом, получаем координаты точек P3 = (x3,y3):
Видео:Взаимное расположение окружностей. Точки пересечения окружностейСкачать

Пересечение двух окружностей
Этот онлайн калькулятор находит точки пересечения двух окружностей, если они существуют
Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.
Формулы для расчета приведены под калькулятором.
Точки пересечения двух окружностей
Первая окружность
Вторая окружность
Видео:Алгоритмы. Пересечение окружностейСкачать

Пересечение окружностей
Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.
При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):
| Случай | Описание | Условие |
|---|---|---|
| Тривиальный случай — окружности совпадают (это одна и та же окружность) | ||
| Окружности не касаются друг друга | r1 + r2″ /> | |
| Одна окружность содержится внутри другой и не касается ее | ||
| Окружности пересекаются в двух точках | Не выполнено ни одно из условий выше | |
| Окружности соприкасаются в одной точке | Частный случай предыдущего |
Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:
Сначала калькулятор находит отрезок a
Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):
И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:
Обратите внимание на разные знаки перед вторым слагаемым
По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres
Видео:Пересечение двух окружностейСкачать

Пересечение двух окружностей
Даны две окружности, каждая определена координатами своего центра и радиусом. Требуется найти все их точки пересечения (либо одна, либо две, либо ни одной точки, либо окружности совпадают).
Видео:9 класс, 8 урок, Взаимное расположение двух окружностейСкачать

Решение
Предположим, не теряя общности, что центр первой окружности — в начале координат (если это не так, то перенесём центр в начало координат, а при выводе ответа будем обратно прибавлять координаты центра). Тогда мы имеем систему двух уравнений:
Вычтем из второго уравнения первое, чтобы избавиться от квадратов переменных:
Таким образом, мы свели задачу о пересечении двух окружностей к задаче о пересечении первой окружности и следующей прямой:
А решение последней задачи описано в соответствующей статье.
Единственный вырожденный случай, который надо рассмотреть отдельно — когда центры окружностей совпадают. Действительно, в этом случае вместо уравнения прямой мы получим уравнение вида 0 = С, где C — некоторое число, и этот случай будет обрабатываться некорректно. Поэтому этот случай нужно рассмотреть отдельно: если радиусы окружностей совпадают, то ответ — бесконечность, иначе — точек пересечения нет.
💥 Видео
Геометрия 9 класс (Урок№10 - Взаимное расположение двух окружностей.)Скачать

1 2 4 сопряжение окружностейСкачать

Точки пересечения графиков линейных функций. 7 класс.ОбразовательныйСкачать

Геометрия В точках пересечения двух окружностей с радиусами 4 и 8 см касательные к ним взаимноСкачать

Черчение. Внутреннее, внешнее и смешенное сопряжение двух окружностей.Скачать

Взаимное расположение окружностей. 7 класс.Скачать

Параметр. Серия 13. Решение задач с окружностями. Касание двух окружностейСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Метод эксцентрических сферСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Алгоритмы. Пересечение отрезков.Скачать

Определение точки пересечения окружности с прямойСкачать