Пусть a( ax, ay) и b( bx, by) – два входных вектора. Вычислим модули этих векторов:
ma = | a| = 
Скалярное произведение векторов также равно произведению их модулей на косинус угла между ними: ( a, b) = | a| * | b| * cos φ. Следовательно
cos φ = 

откуда находится и сам угол. Арккосинус угла лежит в интервале [0; π], поэтому никаких дополнительных вычислений производить не требуется.
Видео:Как находить угол между векторамиСкачать

Реализация алгоритма
Вычисляем угол между двумя векторами по выше приведенной формуле.
ma = sqrt(ax*ax + ay*ay); mb = sqrt(bx*bx + by*by);
Видео:Угол между векторами. 9 класс.Скачать

Практические задачи по Java — для курсов и прочих занятий
Видео:Угол между векторами | МатематикаСкачать

Практические задачи по Java — для курсов и прочих занятий
Несколько вводных слов
Последние несколько лет я читаю курс по программированию на Java. Со временем он менялся — то добавлялись, то выкидывались разные части, менялась последовательность тем, менялся подход к построению плана самих занятий, и так далее. То есть, курс совершенствовался. Одной из основных проблем, возникших при подготовке курса — это задачи. О них и пойдёт речь.
Дело в том, что каждое моё занятие состоит из двух частей. На первой я выступаю в роли лектора — рассказываю с примерами кода о какой-то новой теме (классы, наследование, дженерики и так далее). Вторая часть — практическая. Очевидно, что нет смысла просто рассуждать о программировании, надо программировать. Приоритет на занятиях — решение задач, то есть программирование чего-то как-то. Программирование на занятиях отличается от программирования дома, так как на занятиях можно задать вопрос, показать код, получить быструю оценку кода, комментарии по улучшению, исправлению написанного. Очень легко было найти задачи для самых первых занятий. Задачи на циклы, условные операторы, и ООП (к примеру, написать класс «Собака» или класс «Вектор»). Сервисы вроде leetcode позволяют даже проверить правильность решения таких задач сразу, онлайн. Но какие задачи дать студентам на занятии, которое было посвящено коллекциям? Потокам? А аннотациям? За несколько лет я придумал, или переработал несколько таких задач, и эта статья, по сути, является сборником этих задач (к некоторым задачам прилагается решение).
Конечно, все задачи уже где-то появлялись. Однако, эта статья ориентирована на преподавателей курсов по программированию (для языков, похожих на Java, большинство задач подойдёт), или тех, кто преподаёт программирование частным образом. Эти задачи можно использовать «из коробки» на своих занятиях. Изучающие Java тоже могут попробовать решать их. Но такие решения требуют сторонней проверки и оценки.
Некоторые самые простые задачи, которые уже десятилетия все используют, я тоже включил в эту статью. Пожалуй, для того, чтобы не начинать сразу с абстрактных классов.
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Вычислить угол между двумя линиями без необходимости вычислять наклон? (Джава)
У меня есть две линии: L1 и L2. Я хочу рассчитать угол между двумя линиями. У L1 есть очки: , а у L2 есть очки: .
Как я могу рассчитать угол, образованный между этими двумя линиями, без необходимости вычислять наклоны? Проблема, с которой я сталкиваюсь в настоящее время, заключается в том, что иногда у меня есть горизонтальные линии (линии вдоль оси x), и следующая формула не выполняется (деление на ноль исключения):
где m1 и m2 — наклоны линии 1 и 2 соответственно. Существует ли формула/алгоритм, который может вычислять углы между двумя линиями, не получая исключения деления на ноль? Любая помощь будет высоко оценен.
Это мой фрагмент кода:
Функция atan2 облегчает работу с atan .
Он объявляется как double atan2(double y, double x) и преобразует прямоугольные координаты (x,y) в угол theta из полярных координат (r,theta)
Так что я бы переписал ваш код как
Точечный продукт, вероятно, более полезен в этом случае. Здесь вы можете найти геометрический пакет для Java, который предоставляет несколько полезных помощников. Ниже приведен их расчет для определения угла между двумя трехмерными точками. Надеюсь, это поможет вам начать:
Точечное произведение двух векторов равно косинусу угла времени на длину обоих векторов. Это вычисляет скалярное произведение, делит на длину векторов и использует функцию обратного косинуса для восстановления угла.
Может быть, мой подход к системе координат Android будет кому-то полезен (для хранения точек использовался класс Android PointF)
Возвращает положительное значение в градусах для любого квадранта: 0
Формула для получения угла tan a = (slope1-slope2)/(1+slope1*slope2)
🎬 Видео
9 класс, 17 урок, Угол между векторамиСкачать

11 класс, 5 урок, Угол между векторамиСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Нахождение угла между векторами через координаты. 9 класс.Скачать

Угол между векторамиСкачать

100 тренировочных задач #135 Угол между векторамиСкачать

105. Угол между векторамиСкачать

Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

Угол между векторами | Геометрия 7-9 класс #100 | ИнфоурокСкачать

найти угол между единичными векторамиСкачать

Угол между векторамиСкачать

Математика это не ИсламСкачать

№1039. Диагонали квадрата ABCD пересекаются в точке О. Найдите угол между векторами: а) АВ и АССкачать

#3 Как найти угол между векторами?Скачать
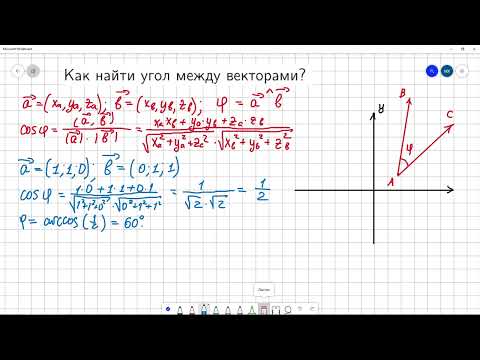
Угол между векторами.Скачать

Геометрия 9 класс (Урок№18 - Угол между векторами. Скалярное произведение векторов.)Скачать

