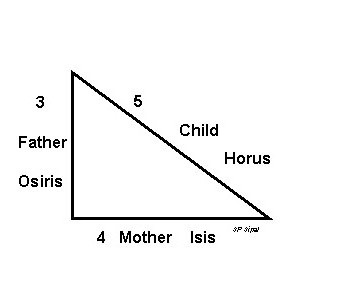
Прямоугольный треугольник с соотношением сторон три на четыре на пять и суммой чисел двенадцать — принято называть Египетским треугольником. Данный треугольник использовался архитекторами древности для достижения пропорции строения.
Уникальностью данного треугольника является то, что произведение квадратов сторон, согласно теореме Пифагора, дают целые числа, то есть: девять, шестнадцать и двадцать пять. Сумма катетов и гипотенузы равняется двенадцати и является единицей кратности, применяемой для выведения прямых углов посредством веревки. Для этого веревку разделяют узлами на три двенадцатых и семь двенадцатых ее длины.
Египетский треугольник является ярким примером семейства «Героновых треугольников». Геронов треугольник — это такой треугольник, площадь которого и длина каждой из сторон выражаются рациональным числом. Рациональное число (лат. rationalis numerus) это такое число, которое можно представить в виде обыкновенной дроби с целым числом в числителе и натуральным числом в знаменателе.
Считается, что название Египетскому треугольнику придумали древние греки. Еще в седьмом – пятом веках да новой эры, греческие философы и ученые бывали в Египте, а многие там обучались. Ярким примером такого обучения можно считать Пифагора Самосского. Который в молодом возрасте, имея рекомендацию правителя Поликрата, отправился в Египет что бы познать тайны египетских жрецов. Благодаря рекомендации, после проведенных испытаний, фараоном Амасисом он был допущен к обучению наукам, которые постигал двадцать два года. Считается, что именно в этот период пытаясь обобщить отношения квадратов, типичных именно египетскому треугольнику, на все прямоугольные треугольники вообще, Пифагор вывел свою знаменитую теорему.
Ярким примером использования египетского треугольника в архитектуре можно считать пирамиду Хефрена. Пирамида Хефрена представляет собой строение имеющее в основе прямоугольный треугольник с соотношением сторон три на четыре на пять и углом наклона баковых граней 53 градуса 12 минут. В древности такое соотношение называлось «Золотым треугольником». Это яркий пример использование теоремы Пифагора. При её использовании квадрат гипотенузы равен двадцати пяти, а катетов соответственно шестнадцать и девять, которые в сумме двадцать пять. Применение данного свойства в строительстве происходит следующим образом. Проводится линия кратная пяти. Затем от одного её края проводится линия кратная четырем, а второго края провести линию кратную трем. Пересекаясь линии образуют углы в девяносто, пятьдесят три градуса тринадцать минут и тридцать шесть градусов восемьдесят шесть минут. Что практически полностью соответствует параметрам пирамиды Хефрена.
Видео:Египетский треугольник. Пифагоровы тройки.Скачать

Египетский треугольник
Видео:Египетский треугольникСкачать

Популярные темы сообщений
Река, которая протекает в городе Воронеже – одна из самых больших и известных рек в Российской Федерации, она кстати еще и является одним из многочисленных притоков Дона и делит Воронеж на две равные части,
День народного единства России является государственным праздником. Он отмечается обычно 4 ноября. В этот день никто не работает. Впервые о нем стало известно в 2004 году. Именно данный праздник помогает всем народам объединиться в одну
Герань – неприхотливое растение рода семейства Гераниевые. Геранью также могут называть похожее растение из рода Пеларгония, но того же семейства. Название происходит от греческого слова «журавль» — geranion,
Видео:Что такое египетский треугольник?Скачать

Египетский треугольник — доклад сообщение
Со времен античности до настоящего времени в разных сферах жизнедеятельности человека существует огромное количество бесценных открытий.
Среди них почетное место занимает всемирно известный «Египетский» треугольник. вавилонская геометрия славилась тем, что в ее пределах велась работам прямоугольным треугольником с сочетанием 3:4:5.
История его появления связана с наблюдениями эллинов за основой пирамиды Хеопса в Египетском государстве еще в v веке до г. э. По одной из версий название этому треугольнику было дано древними греками. Второе ее название — «Золотой треугольник».
Среди этих людей был ученый Пифагор Саросский, который особое внимание обратил на формы этой великой постройки. Так повелось, что с древних пор именно этот треугольник архитекторы применяли для достижения определенных пропорций строения. Теорема Пифагора, которая стала открытием, используется в настоящее время. Ученый изначально делал попытку обобщения отношения квадратов, характерных для египетского треугольника.
В строительстве правило его использования незаменимо. Это связано с тем, что при определенном произведении линий образуется угол в 90, 53 градусов 13 минут и 36 градусов 86 минут. Именно такие параметры имеет всемирно известная пирамида Хефена.
Особенностями египетского треугольника является его площадь и стороны — целые числа, также при использовании обычной веревки можно изобразить этот треугольник без труда. К этому способу обращались зачастую землемеры, которые с ее помощью выводили прямой угол.
В настоящее время также рабочие, связанные со стройкой, нередко обращаются к этой методике, чтобы при необходимости получить ровные прямые углы. Это было связано с тем, что в далеком прошлом было недостаточно инструментов для качественного процесса строительства зданий.
Таким образом, «Египетский треугольник» — это уникальная геометрическая конструкция, известная с давних пор. Прообразом этой фигуры является одна из египетских пирамид, на которую обратил внимание во время своего путешествия математик древности — Пифагор.
Ее особенность состоит в том, что, например, обычная идея построить дом возможна без обращения к угольнику или транспортиру. Грамотный подход и знания строителя, правильное соотношение всех углов возможно при грамотном подходе с построением этого треугольника.
Видео:Египетский треугольникСкачать

Картинка к сообщению Египетский треугольник
Видео:Делаем Египетский треугольник из верёвочки с узелками. Геометрия для детей. Математика - это красивоСкачать

Популярные сегодня темы
«Деревянным золотом» называют народное прикладное искусство – хохломскую роспись. Она появилась в 17 веке в селе Хохлома Нижегородской области. Ученые предполагают, что первых мастеров вдохно
Спорт является не только приятным времяприпровождением, но и очень полезным занятием для нашего здоровья. Люди, которые занимаются спортом, реже болеют и обладают прекрасными внешними данными
Государство Османская Империя было образовано в 1299 году на северо-западе Малой Азии. Сейчас это государство находится на турецких территориях и называется Турцией.
Кем быть – этот вопрос занимает практически каждого человека, ведь человек определяется через собственные дела. Фактически мы можем определить человека через плоды его деятельности
Джеймс Кук (1728-1779 гг.) относится к известным английским мореплавателям, совершившим в своей биографии большое количество морских экспедиций.
Мир растений каждого материка нашей планеты уникален по-своему. Необычный растительный мир Австралии имеет свои особенности, где таится немало прекрасных моментов и опасностей. Представители
Видео:Египетский треугольникСкачать

Египетский треугольник — загадка древности
Известный математик Пифагор совершил множество различных открытий, но большинству людей, которым не приходится регулярно сталкиваться с алгеброй и геометрией, он известен благодаря своей теореме. Ученый открыл ее, пребывая в Египте, где его очаровала красота и изящность пирамид, а это, в свою очередь, натолкнуло его на мысль о том, что в их формах прослеживается определенная закономерность.
Видео:Египетский треугольникСкачать

История открытия
Своим названием египетский треугольник обязан эллинам, которые часто посещали Египет в VII-V веках до н. э., среди них был и Пифагор. Основой пирамиды Хеопса является прямоугольный многоугольник, а
Видео:Пифагоровы тройки 1. Египетский треугольникСкачать

Применение
Египетский треугольник с древности пользовался популярностью в архитектуре и строительстве.
Соотношение сторон этого треугольника 3:4:5 приводит к тому, что он является прямоугольным, т. е. один угол равен 90 градусам, а два других – 53,13 и 36,87 градусам. Прямым является угол между сторонами, соотношение которых равно 3:4.
Видео:НИКОЛА ТЕСЛА Раскрывает Жуткую Тайну Египетских Пирамид / Ученые Не Могут Это ОбъяснитьСкачать

Доказательство
При помощи некоторых простых вычислений можно доказать, что треугольник является прямоугольным. Если следовать теореме обратной той, которую создал Пифагор, т. е. в случае, если сумма квадратов двух сторон будет равняться квадрату третьей, то он прямоугольный, а поскольку его стороны приводят к равенству 3 2 х 4 2 = 5 2 , следовательно, он является прямоугольным.
Подводя итог, надо отметить, что египетский треугольник, свойства которого уже в течение многих столетий известны человечеству, на сегодняшний день продолжает использоваться в архитектуре. Это вовсе неудивительно, ведь такой способ гарантирует точность, которая очень важна при строительстве. Кроме этого, он очень прост в использовании, что тоже значительно облегчает процесс. Все преимущества использования этого метода прошли проверку веками и остаются популярными до сих пор.
📽️ Видео
9 класс, 12 урок, Теорема о площади треугольникаСкачать

Полуокружность в египетском треугольнике.Скачать
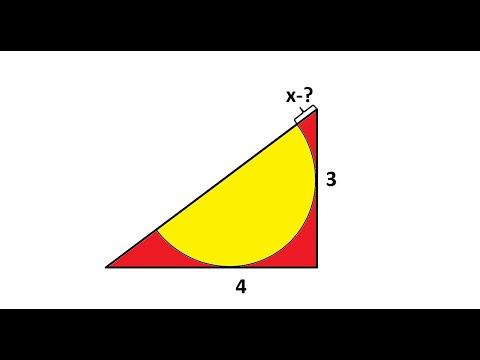
Египетский треугольник, свойстваСкачать

Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Теорема ПифагораСкачать
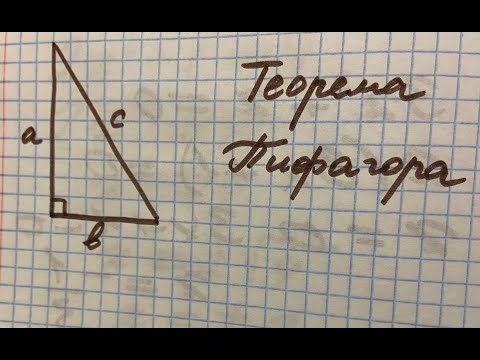
Новая конструкция египетского треугольникаСкачать

8 класс, 16 урок, Теорема ПифагораСкачать

Как ЭТО Возможно? Топ 10 Фактов о Египетском Сфинксе, Которые Вы Не ЗналиСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Интересная задача по планиметрии про египетский треугольникСкачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать