В выпуклом четырехугольнике длины диагоналей равны 1 и 2 найдите площадь четырехугольника

Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

В выпуклом четырехугольнике длины диагоналей равны 1 и 2 найдите площадь четырехугольника

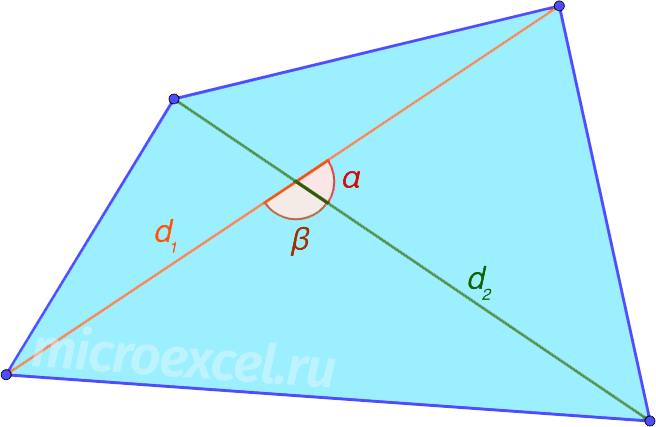
Найдите площадь выпуклого четырёхугольника с диагоналями 3 и 4, если отрезки, соединяющие середины его противоположных сторон, равны.

Пусть ABCD — данный четырёхугольник, O — середина стороны AB, K — середина стороны BC, P — середина стороны CD, H — середина стороны DA. Проведём диагонали AC и BD и отрезки OK, KP, PH и HO, последовательно соединяющие середины сторон четырёхугольника. Тогда, по свойству средней линии треугольника, отрезки OK и PH параллельны диагонали AC и равны её половине, а отрезки KP и HO параллельны диагонали BD и равны её половине. Поэтому OKPH — параллелограмм. А так как, по условию задачи, его диагонали KH и OP равны, то OKPH — прямоугольник, и угол OKP — прямой. Отсюда следует, что и угол между диагоналями AC и BD тоже прямой, и, следовательно, площадь четырёхугольника ABCD будет равна половине произведения его диагоналей, то есть

.

Видео:№529. Диагонали четырехугольника равны 16 см и 20 см и пересекаются под углом в 30°. Найдите площадьСкачать

Г. И. Ковалева Итоговое повторение курса планиметрии с привлечением метода ключевой задачи

Главная > Документ

Треугольник, образованный основаниями высот

данного остроугольного треугольника

Ключевая задача. АА 1 , ВВ 1 , СС 1 – высоты остроугольного треугольника АВС . Докажите, что а) треугольники АА 1 С и ВВ 1 С подобны; б) треугольники АВС и А 1 В 1 С подобны и .

Д о к а з а т е л ь с т в о. Треугольники АА 1 С и ВВ 1 С подобны по двум углам.

Из этого следует, что или . Треугольники АВС и А 1 В 1 С подобны, так как и – общий и .

Задача 1. АА 1 , ВВ 1 , СС 1 – высоты остроугольного треугольника АВС . Докажите, что АА 1 , ВВ 1 , СС 1 – биссектрисы углов треугольника А 1 В 1 С 1 .

Д о к а з а т е л ь с т в о. Треугольники АВС и А 1 В 1 С подобны, следовательно, .

Треугольники АВС и А 1 ВС 1 подобны, следовательно, .

. Следовательно, АА 1 – биссектриса .

Задача 2. АА 1 , ВВ 1 , СС 1 – высоты остроугольного треугольника АВС . Докажите, что .

Д о к а з а т е л ь с т в о. .

, , .

Имеем или . . Откуда .

Задача 3. АА 1 , ВВ 1 , СС 1 – высоты остроугольного треугольника АВС . Докажите, что отношение периметров треугольников А 1 В 1 С 1 и АВС равно , где r и R – радиусы соответственно вписанной и описанной окружностей около треугольника АВС .

Р е ш е н и е. Так как , и , то .

. С другой стороны

, где О – центр описанной около треугольника АВС окружности.

Найдем площади треугольников АОВ , ВОС и АОС .

.

Анологично, , .

.

Приравнивая площади, получим .

Задача 4. Отрезки, соединяющие основания высот остроугольного треугольника, равны 8, 15 и 17. Найдите стороны треугольника.

Р е ш е н и е. Так как , то треугольник А 1 В 1 С 1 – прямоугольный. Следовательно, , .

, .

, .

Используя формулу понижения степени , найдем . , .

Рассуждая аналогично, можно найти сторону ВС . , , .

О т в е т: ; ; .

Задачи для самостоятельного решения

1. Высота АН и СК остроугольного треугольника АВС пересекаются в точке D , причем , , . Найдите сторону ВС .

2. В остроугольном треугольнике АВС проведены высоты АА 1 , ВВ 1 , и СС 1 . Докажите, что .

3. Длина основания равнобедренного треугольника равна 12, а боковой стороны – 18. К боковым сторонам треугольника проведены высоты. Найдите длину отрезка с концами в основаниях высот.

О т в е т: .

4. В остроугольном треугольнике АВС проведены высоты СС 1 и АА 1 . Известно, что и . Найдите радиус окружности, описанной около треугольника С 1 ВА 1 .

О т в е т: .

5. В остроугольном треугольнике АВС . На стороне ВС как на диаметре построена окружность, пересекающая стороны АВ и ВС соответственно в точках P и Q . Найдите отношение площадей треугольников ABC и APQ .

О т в е т: .

Четырехугольник, вершины которого

являются серединами сторон данного четырехугольника

Ключевая задача. Середины сторон произвольного четырехугольника являются вершинами параллелограмма.

Д о к а з а т е л ь с т в о. Пусть ABCD – выпуклый четырехугольник.

M , N , P , K – середины сторон АВ, ВС, CD и А D соответственно.

Отрезок MN параллелен диагонали АС и равен ее половине по свойству средней линии.

Аналогично, отрезок PK параллелен АС и равен ее половине. Следовательно, отрезки MN и PK равны и параллельны. По признаку MNPK – параллелограмм.

Для невыпуклого и пространственного четырехугольников доказательство аналогичное.

1. Если ABCD – выпуклый четырехугольник и M , N , P , K – середины его сторон АВ, ВС, CD и AD соответственно, то .

Д о к а з а т е л ь с т в о. Треугольники MBN и АВС подобны, следовательно, . Аналогично, . .

Аналогично, , , .

Имеем, .

2. Середины сторон прямоугольника являются вершинами ромба.

3. Середины сторон равнобедренной трапеции являются вершинами ромба.

4. Середины сторон ромба являются вершинами прямоугольника.

Осмыслению ключевой задачи будут способствовать вопросы: Каким условиям должны удовлетворять диагонали данного четырехугольника, чтобы середины его сторон были вершинами прямоугольника, ромба, квадрата? Докажите, что середины сторон трапеции со взаимно перпендикулярными диагоналями являются вершинами прямоугольника.

Составьте обратную задачу. Верна ли она?

Задача 1. Докажите, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

Д о к а з а т е л ь с т в о. Пусть медианы АА 1 и СС 1 пересекаются в точке О . Отметим точки К и Р – середины отрезков АО и СО . Тогда точки К, Р, С 1 и А 1 середины сторон невыпуклого четырехугольника

АВСО . Следовательно, по ключевой задаче КРС 1 А 1 – параллелограмм. Его диагонали точкой пересечения делятся пополам. Тогда .

Рассуждая аналогично, докажем, что медианы АА 1 и ВВ 1 пересекаются в точке Q и . Так как отрезок АА 1 делится в отношении 2:1, считая от точки А, однозначно, то точки О и Q совпадают. Следовательно, медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

Задача 2. Докажите, что отрезки, соединяющие середины сторон скрещивающихся ребер тетраэдра пересекаются в одной точке.

Д о к а з а т е л ь с т в о. По ключевой задаче MKPN и MLPR – параллелограммы. Их диагонали пересекаются в одной точке и делятся ею пополам.

Задача 3. Диагонали трапеции взаимно перпендикулярны, длина одной из них равна 6. Длина отрезка, соединяющего середины оснований, равна 5. Найдите площадь трапеции.

Р е ш е н и е. Пусть M и P – середины боковых сторон трапеции. Тогда по ключевой задаче MNPK – прямоугольник. Так как , то . По теореме Пифагора из прямоугольного треугольника MNK . Тогда , а .

Задача 4. В выпуклом четырехугольнике длины диагоналей 2 и 4. Найдите площадь четырехугольника, зная, что длины отрезков, соединяющих середины противоположных сторон равны.

Р е ш е н и е. По ключевой задаче MNPK – параллелограмм. Так как его диагонали равны, то MNPK – прямоугольник. Диагонали данного выпуклого четырехугольника параллельны сторонам прямоугольника и, следовательно, перпендикулярны. Найдем площадь выпуклого четырехугольника как половину произведения диагоналей на синус угла между ними. .

Задача 5. В выпуклом четырехугольнике ABCD длина отрезка, соединяющего середины сторон AB и CD , равна одному метру. Прямые BC и А D перпендикулярны. Найдите длину отрезка, соединяющего середины диагоналей AC и В D .

Р е ш е н и е. Обозначим через M , N , P , K – середины сторон АВ, В D , CD и АС соответственно. Тогда MK ║ NP ║ BC как средние линии треугольников BAC и BDC . Аналогично, MN ║ KP ║ AD . Так как прямые BC и А D перпендикулярны, то параллельные им прямые МК и MN также перпендикулярны. Следовательно, параллелограмм MNPK является прямоугольником и .

Задачи для самостоятельного решения

1. Найдите площадь четырехугольника, если известно, что отрезки, соединяющие середины его смежных сторон, равны 2 и 3, а угол между ними 30 0 .

2. Найдите площадь четырехугольника, если известно, что отрезки, соединяющие середины его противоположных сторон, равны 3 и 4, а длина одной из диагоналей четырехугольника равна 5.

3. Найдите площадь четырехугольника, если известно, что отрезки, соединяющие середины его смежных сторон, равны 3 и 4, а длина одного из отрезков, соединяющих середины противоположных сторон, равна 5.

4. В равнобедренной трапеции длина средней линии равна 5см, а диагонали взаимно перпендикулярны. Найдите площадь трапеции.

5. В выпуклом пятиугольнике ABCDE с единичными сторонами середины P , Q сторон AB , CD и S , T сторон BC , DE соединены отрезками PQ и ST . Пусть M и N – середины отрезков PQ и ST . Найдите длину MN .

Видео:Задание 26 Площадь четырехугольникаСкачать

Нахождение площади выпуклого четырехугольника: формула и пример

Выпуклый четырехугольник – это геометрическая фигура, полученная путем соединения на плоскости четырех точек, которые не должны лежать на одной прямой. При этом образованные таким образом стороны не должны пересекаться.

Видео:Найдите длины диагоналей параллелограмма, построенного на векторах a=(1;-1;-4) и b=(-5;3;8)Скачать

Формула вычисления площади

По диагоналям и углу между ними

Площадь (S) выпуклого четырехугольника равняется одной второй (половине) произведения его диагоналей и синуса угла между ними.

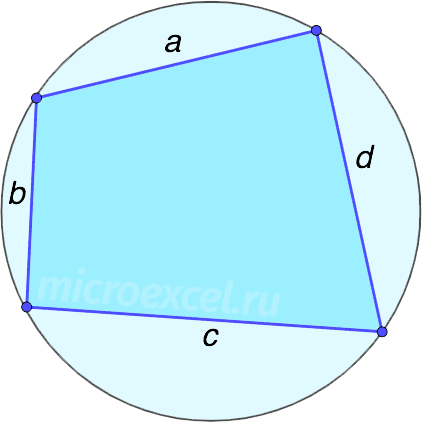
По четырем сторонам (формула Брахмагупты)

Чтобы воспользоваться формулой, необходимо знать длины всех сторон фигуры. Также вокруг четырехугольника должна быть возможность описать окружность.

p – полупериметр, вычисляется следующим образом:

По радиусу вписанной окружности и сторонам

Если в четырехугольник можно вписать окружность, вычислить его площадь можно, воспользовавшись формулой:

S = p ⋅ r

r – радиус окружности.

Видео:ОГЭ Задание 24 Площадь выпуклого четырехугольника с перпендикулярными диагоналямиСкачать

Пример задачи

Найдите площадь выпуклого четырехугольника, если его диагонали равны 5 и 9 см, а угол между ними составляет 30°.

Решение:
Подставляем в формулу известные нам значения и получаем: S = 1/2 * 5 см * 9 см * sin 30° = 11,25 см 2 .

🎬 Видео

Площадь ромба. Легче понять...Скачать

ОГЭ по математике. Площадь четырехугольника можно вычислить по формуле (вар. 5)Скачать

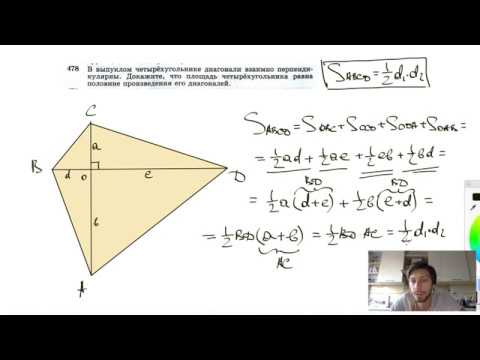
№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать

ОГЭ без рекламы математика 11 и 12 вариант задача 25Скачать

Площадь четырёхугольника через диагоналиСкачать

Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Геометрия Найдите площадь выпуклого четырехугольника диагонали которого равны 3√3 см и 4 см а уголСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Геометрия: считаем ПЛОЩАДЬ ЧЕТЫРЕХУГОЛЬНИКА | Математика 8-11 классСкачать

Площади фигур. Сохраняй и запоминай!#shortsСкачать

Диагонали четырехугольника равны 4 и 5.Скачать

Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

Площадь ромба 📐 А бесплатный файлик в комментарияхСкачать

Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Площадь квадрата через диагональ 📐 Полезный файлик в комментариях)Скачать