В каком отношении находятся множества а и в а множество четырехугольников

Видео:Множества и операции над нимиСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Лекция 2. Отношения между множествами.

Между двумя множествами существует пять видов отношений.

Если множества А и В не имеют общих элементов, то говорят, что эти множества не пересекаются и записывают этот факт в виде А∩В = ∅ . Например, А = < a , c , k >, В = < d , e , m , n >, общих элементов у этих множеств нет, поэтому множества не пересекаются.

Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются и записывают А∩В≠ ∅ . Например, множества А = < a , c , k > и В = < c , k , m , n > пересекаются, т. к. у них есть общие элементы c , k .

Множество В является подмножеством множества А, если каждый элемент множества В является также элементом множества А. Пустое множество является подмножеством любого множества. Само множество является подмножеством самого себя. (пишут В ⊂ А)

Пустое множество и само множество называют несобственными подмножествами . Остальные подмножества множества А называются собственными. Для каждого множества, состоящего из n элементов можно образовать 2 n подмножеств. Если рассматривают лишь подмножества некоторого множества U, то U называют универсальным множеством.

Если множества А и В состоят из одних и тех же элементов, то они называются равными.

Например, А = < a , c , k , m , n > и В = < m , n , a , c , k >, А = В.

Существует пять случаев отношений между двумя множествами. Их можно наглядно представить при помощи особых чертежей, которые называются кругами или диаграммами Эйлера-Венна.

Разбиение множества на классы называют классификацией.

Классификацию можно выполнять при помощи свойств элементов множества. Если выбирается только одно свойство, то такую классификацию называют дихотомической . Например, натуральные числа можно разбить на четные и нечетные. Буквы русского языка можно разбить на гласные и не гласные. Вообще, если на множестве Х задано одно свойство А, то это множество разбивается на два класса: первый класс – объекты, обладающие свойством А, второй класс – объекты, не обладающие свойством А.

Если элементы множества обладают двумя независимыми свойствами, то все множество разбивается на 4 класса. Например, на множестве натуральных чисел заданы два свойства: «быть кратным 2» и «быть кратным 3». При помощи этих свойств в множестве N можно выделить два подмножества А и В. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 6). Тогда в первый класс войдут числа, кратные 2 и 3, во второй – кратные 2, но не кратные 3, в третий – кратные 3, но не кратные 2, в четвертый – не кратные 2 и не кратные 3.

П р и м е р 1. Пусть Х – множество четырехугольников, А, В и С – его подмножества. Можно ли говорить о разбиении множества Х на классы А, В и С, если:

а) А – множество параллелограммов, В – множество трапеций, С – множество четырехугольников, противоположные стороны которых не параллельны;

б) А – множество параллелограммов, В – множество трапеций, С – множество четырехугольников, имеющих прямой угол?

Р е ш е н и е. а) Множества А, В и С попарно не пересекаются. Действительно, если у четырехугольника, противоположные стороны не параллельны, то он не может быть параллелограммом или трапецией. В параллелограмме противоположные стороны попарно параллельны, поэтому он не может принадлежать ни множеству В, ни множеству С. Наконец, в трапеции две противоположные стороны параллельны, а две другие не параллельны, поэтому трапеция не может принадлежать ни множеству А, ни множеству С. Объединение множеств А, В и С даст все множество четырехугольников. Условия классификации выполнены, множество всех четырехугольников можно разбить на параллелограммы, трапеции и четырехугольники, противоположные стороны которых не параллельны.

б) Множества А и В не пересекаются, но множества А и С имеют общие элементы, примером может служить прямоугольник, множества В и С тоже пересекаются: общим элементом является прямоугольная трапеция. Следовательно, нарушено первое условие классификации. Не выполняется и второе условие, так как некоторые четырехугольники не попадают ни в одно из подмножеств А, В или С, таким является четырехугольник с непараллельными сторонами и непрямыми углами. В этом случае множество Х на классы А, В и С не разбивается.

Задания для самостоятельной работы по теме:

Приведите примеры множеств А, В, С, если отношения между ними таковы:

2. Образуйте все подмножества множества букв в слове «крот». Сколько подмножеств получилось?

3 . Из множества N выделили два подмножества: А – подмножество натуральных чисел, кратных 3, и В – подмножество натуральных чисел, кратных 5. Постройте круги Эйлера для множеств N , A , B ; установите, на сколько попарно непересекающихся множеств произошло разбиение множества N ; укажите характеристические свойства этих множеств.

5. Имеется множество блоков, различающихся по цвету (красные, желтые, зеленые), форме (круглые, треугольные, прямоугольные), размеру (большие, маленькие). На сколько классов разбивается множество, если в нем выделены подмножества: А – круглые блоки, В – зеленые блоки, С – маленькие блоки? Сделайте диаграмму Эйлера и охарактеризуйте каждый класс.

6. Известно, что А – множество спортсменов класса, В – множество отличников класса. Сформулируйте условия, при которых: а) А ∩В=Ø

7. Пусть Х= < x N/ 1 x 15>. Задайте с помощью перечисления следующие его подмножества:

А – подмножество всех четных чисел;

В – подмножество всех нечетных чисел;

С – подмножество всех чисел, кратных 3;

D – подмножество всех чисел, являющихся квадратами;

Видео:Множество. Элементы множества. 5 класс.Скачать

(Задание 5) Отношения между множествами всех выпуклых четырехугольников (А), параллелограммов (В), прямоугольников (С), ромбов (Д) и квадратов (Е) изображены на рисунке 6?

Математика | 10 — 11 классы

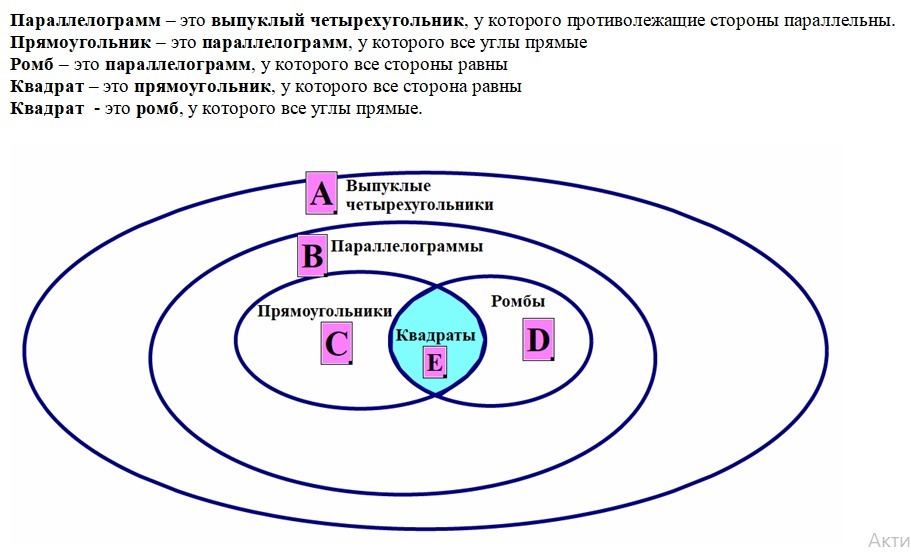
(Задание 5) Отношения между множествами всех выпуклых четырехугольников (А), параллелограммов (В), прямоугольников (С), ромбов (Д) и квадратов (Е) изображены на рисунке 6.

Покажите каждое из множеств.

Параллелограмм – это выпуклый четырехугольник, у которого противолежащие стороны параллельны.

Прямоугольник – это параллелограмм, у которого все углы прямые

Ромб – это параллелограмм, у которого все стороны равны

Квадрат – это прямоугольник, у которого все сторона равны

Квадрат — это ромб, у которого все углы прямые.

Видео:Подмножество. Операции над множествами (пересечение, объединение множеств) – 8 класс алгебраСкачать

В — МНОЖЕСТВО ТРЕУГОЛЬНИКОВ С — МНОЖЕСТВО ЧЕТЫРЕХУГОЛЬНИКОВ Д — МНОЖЕСТВО ПРЯМОУГОЛЬНИКОВ Е — МНОЖЕСТВО КВАДРАТОВ А — МНОЖЕСТВО МНОГОУГОЛЬНИКОВ?

В — МНОЖЕСТВО ТРЕУГОЛЬНИКОВ С — МНОЖЕСТВО ЧЕТЫРЕХУГОЛЬНИКОВ Д — МНОЖЕСТВО ПРЯМОУГОЛЬНИКОВ Е — МНОЖЕСТВО КВАДРАТОВ А — МНОЖЕСТВО МНОГОУГОЛЬНИКОВ.

Какие из этих множеств являются подмножествами других множеств?

Видео:9 класс, 2 урок, Множества и операции над нимиСкачать

ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА ЗАВТРА СДАВАТЬ?

ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА ЗАВТРА СДАВАТЬ!

Даны множества А, В, С.

Изобразите отношения между ними.

Укажите характеристическое свойство множеств АUВ, А∩С, А В, А ∩ (В С) : № 11.

А – множество учащихся в школе ;

В – множество девочек в школе ;

С – множество учащихся третьих классов в этой школе.

А – множество натуральных чисел ;

В – множество натуральных чисел, кратных 5 ;

С – множество натуральных чисел, кратных 4.

А – множество параллелограммов ;

В – множество четырехугольников ;

С – множество прямоугольников.

А – множество прямоугольников ;

В – множество четырехугольников ;

С – множество квадратов.

А – множество треугольников ;

В – множество прямоугольных треугольников ;

С – множество равнобедренных треугольников.

А – множество трапеций ;

В – множество параллелограммов ;

С – множество четырехугольников, имеющих прямой угол.

А – множество прямоугольных треугольников ;

В – множество равносторонних треугольников ;

С – множество равнобедренных треугольников.

А – множество натуральных чисел, кратных 5 ;

В – множество натуральных чисел, кратных 3 ;

С – множество натуральных чисел, кратных 4.

А – множество натуральных чисел, кратных 2 ;

В – множество натуральных чисел, кратных 3 ;

С – множество натуральных чисел, кратных 5.

А – множество параллелограммов ;

В – множество квадратов ;

С – множество ромбов.

Видео:Множества. Операции над множествами. 10 класс алгебраСкачать

Как может называться множество квадрат ромб круг?

Как может называться множество квадрат ромб круг?

Видео:Пересечение множеств. Объединение множеств. 5 класс.Скачать

Найдите на рисунке все параллелограммы, ромбы, прямоугольники, квадраты?

Найдите на рисунке все параллелограммы, ромбы, прямоугольники, квадраты!

Видео:Отображения множествСкачать

Решите систему неравенств?

Решите систему неравенств.

На каком из рисунков изображено множество ее решений?

Видео:Числовые множества, 6 классСкачать

Какой четырехугольник не имеет оси симметрии?

Какой четырехугольник не имеет оси симметрии?

A) ромб б) прямоугольник в) параллелограмм г) квадрат.

Видео:Математика. 2 класс. Множество и его элементы /14.12.2020/Скачать

Какие из данных четырехугольников не являются параллелограммами 1 квадрат 2 прямоугольник 3 ромб 4 трапеция?

Какие из данных четырехугольников не являются параллелограммами 1 квадрат 2 прямоугольник 3 ромб 4 трапеция.

Видео:Теория множеств. Что такое множествоСкачать

Построй диаграмму Венна для множества А, В, С, Д, где А — множество всех четырехугольников, В — множество ромбов, С — множество квадратов, д — множество прямоугольников?

Построй диаграмму Венна для множества А, В, С, Д, где А — множество всех четырехугольников, В — множество ромбов, С — множество квадратов, д — множество прямоугольников.

Видео:Как изображать множества на диаграммахСкачать

Запиши множество острых , множество прямых и множество тупых углов на рисунке ?

Запиши множество острых , множество прямых и множество тупых углов на рисунке .

Есть ли среди данных фигур прямоугольники .

Из букв входящих в каждой множество составь слова.

Видео:Алгебра 8 класс (Урок№38 - Множества чисел.)Скачать

Запиши множества острых, множество прямых и множество тупых углов на рисунке?

Запиши множества острых, множество прямых и множество тупых углов на рисунке.

Есть ли среди данных фигур прямоугольники?

На этой странице находится ответ на вопрос (Задание 5) Отношения между множествами всех выпуклых четырехугольников (А), параллелограммов (В), прямоугольников (С), ромбов (Д) и квадратов (Е) изображены на рисунке 6?, из категории Математика, соответствующий программе для 10 — 11 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Математика. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

Петя прочитал в 1 день 80страниц, во 2 день 25 страниц и в 3 день 60 страниц. Сколько страниц прочитал Петя за 3 дня? У Кати Было 140 рублей. На 50 рублей она купила бананов . Сколько денег осталось у Кати? К автопарке было 90 автобусов. 20 авт..

Видео:Простейшие операции над множествамиСкачать

Упражнения к главе 2

D= <* | х — квадрат целого числа>.

Запишите множества Си/), используя только математические символы.

• 90. «Прочитайте» множества А = <л| .v:4> и В = <xeZ х 2:4>. Равны ли эти множества? Является ли одно из них подмножеством другого? Обоснуйте. Отметим, что выражение л::4 означает, что число х целое и имеет вид Ап для некоторого целого числа п.
• 91. Докажите, что множество В = <xeZ х 2:4> не равно множеству С=<лгеК | х 2: Л].
• 92. «Прочитайте» следующие подмножества множества всех точек на плоскости:

S= <ХAY=3>, О — фиксированная точка;

Р= <X| расстояние от Xдо прямой / равно 5>, / — фиксированная прямая;

Т = , АВ — данный отрезок;

L= <ХХ —внутренняя точка угла АВС, равноудаленная от его сторон>, /.АВС — данный угол.

Что представляют собой на плоскости множества S, Р, Т и /,?

• 93. Запишите символически множества, заданные характеристическим свойством Р(х), где х — переменная по множеству натуральных чисел.
• 1) Р(х) = «х — четное число».
• 2) Р(х) = «х — нечетное число».
• 3) P(x) = «х при делении на 4 даст остаток 2».
• 94. Запишите символически множества, заданные характеристическим свойством Р(х), где х — переменная по множеству действительных чисел. Изобразите эти множества на числовой прямой.
• 1) Р(х) = «Числа х и 5 находятся на числовой прямой на расстоянии, равном 7».
• 2) Р(х) = «Числа х и 5 находятся на числовой прямой на расстоянии не более 7».
• 3) Р(х) = «Число х удалено от числа а на расстояние менее г, но более d», здесь a,r,d- фиксированные числа.
• 95. Запишите символически множества, заданные указанными характеристическими свойствами:

Р(х) = «Целое число л: представимо в виде произведения двух натуральных чисел, больших 1».

Q(x) = «Действительное число х представимо в виде частного двух целых чисел».

Что это за множества?

• 96. Какой из знаков е, с, = можно поставить между множествами 0 и ?
• 97. Какие из знаков е, с можно поставить между следующими выражениями:
• 1) 2 N 2) N 3)0 N 4) N ?
• 98. Соедините множества А и В знаком включения:

• 2) А =0>, В = <xeZ| х 2 H-2 | AreZ>;
• 4) и .
• 102. В каком отношении находятся следующие пары множеств А и В (пересекаются или нет, связаны ли отношением включения, равны или нет)? Поясните почему.
• 1) А — множество всех натуральных чисел, каждое из которых представимо в виде суммы двух натуральных чисел,

В — множество всех натуральных чисел, больших 1.

2) А — множество всех натуральных чисел,

В — множество всех квадратов натуральных чисел.

3) А — множество всех простых чисел,

В — множество всех квадратов простых чисел.

4) А — множество всех ромбов,

В множество четырехугольников с пересекающимися диагоналями.

5) А — множество всех прямоугольников,

В — множество всех квадратов.

6) А — множество всех равносторонних треугольников,

В — множество всех равнобедренных треугольников.

7) А — множество прямоугольных треугольников,

В — множество всех остроугольных треугольников.

103. Методом двойного включения докажите равенство следующих пар множеств:

• 2) Пусть х, у — целые числа и х +у = z. А — множество общих делителей чисел .V и у₉ В — множество общих делителей чисел у и z.
• 104. Равны ли множества А =<3//+2 | neN] и В =?
• 105. Даны три множества: А — множество разносторонних треугольников, Л₂ — множество равнобедренных треугольников, Л₃ — множество равносторонних треугольников. Образуют ли множества Аь Л₂, Аз разбиение множества всех треугольников на классы?
• 106. Разбейте множество всех рациональных чисел на 3 класса.
• 107. Разбейте множество всех целых чисел на 5 классов.
• 108. Рассмотрите всевозможные разбиения трехэлементного множества S= <a_yb,c> на 2 класса; на 3 класса.
• 109. Разбейте множество А =на классы так, чтобы выполнялось требование: числа л: и у лежат в одном классе тогда и только тогда, когда они имеют одно и то же количество натуральных делителей.
• 110. Образует ли система множеств Z (целых чисел), Q (рациональных чисел), I (иррациональных чисел) разбиение множества R действительных чисел?
• 111. Разбейте множество R на 2 класса; на 4 класса.
• 112. Перечислите элементы множеств:

• 113. На множестве всех цифр от 0 до 9 определены множества А = , В =, С= . Найдите множества А(ВС) и (АВ)С. Какой отсюда можно сделать вывод?
• 114. На множестве всех цифр от 0 до 9 определены множества А = <хх — четная цифра>, В = J2″ 10 AjB, АглВ, АВ, ВА_Ч А , В , А®В.
• 115. Даны числовые множества А =и С = <xeR | 0 A(BkjC) = (АВ)п(АС) двумя способами (поэлементно и используя законы алгебры множеств). Сделайте иллюстрации на диаграммах Эйлера.
• 127. Ассоциативна ли операция симметрической разности множеств?
• 128. Проверьте справедливость следующих равенств множеств:

129. Докажите следующие равенства множеств методом двойного включения:

• 130. Проверьте, является ли операция объединения множеств дистрибутивной относительно разности.
• 131. Известно, что множества А и В не пересекаются. Чему равны множества АВ, АсВ’? Докажите.
• 132. Известно, что А включено в В. Найдите множества АВ, АпВ, А’иВ. Обоснуйте ответ, опираясь на соответствующие определения.
• 133. По условию предыдущей задачи можно сформулировать три утверждения, начинающихся словами «Если А включено в /?, то. ». Для каждого из них сформулируйте обратное утверждение и докажите его истинность.
• 134. Приведите пример множеств А, В и С, опровергающий утверждение: «Если AkjC — BjC, то А = В».
• 135. Известно, что множества А, В и С удовлетворяют равенству
• ( AkjB)C = (АС)иВ. Найдите необходимое условие, которому

удовлетворяют множества А, В и С. Является ли это условие достаточным?

• 136. Известно, что С = AkjB. Чему равно множество (АС)и(ВС) ?
• 137. Докажите следующие утверждения:
• 1) если А включено в С, то Аи(ВпС) = (АиВ)пС;
• 2) если множества А и С не пересекаются, то (АиВ)С = Аи(ВС).
• 138. Докажите утверждения:

• 139. С помощью диаграмм Эйлера изобразите отношения между следующими множествами: А — множество всех прямоугольников, В — множество всех ромбов, С — множество всех параллелограммов, D — множество всех трапеций, Е — множество всех четырехугольников. Найдите множество АпВ.
• 140. Проанализируйте отношения между множествами А, В, С. Изобразите их на кругах Эйлера. Перечислите все элементы множества X в каждом из случаев:
• 1) А — множество всех натуральных чисел, В — множество всех составных чисел, С= 20>. Множество Х= A(B^jC).
• 2) А =-1>, В = N, С = Z. Множество Х= (AnQB.
• 3) А = <xeZ| х -10>, С = . Множество X = (АпВ)пС.
• 4) А = <xeZ| *:4>, В = <xeZ .*:6>, С= <xeZ 0 |х-у|>3. Укажите свойства этою отношения. Задайте отношение р на множестве// = перечислением пар.
• 142. Задайте отношение р на множестве А графически на диаграмме Эйлера, обозначая связь хру стрелкой, ведущей от х к у. Такой схематичный рисунок называется графом отношения. Определите свойства р:

• б) А =, хру (х + у) — четное число.
• 143. Отношение р на множестве А задано правилом: хру ||х| — у| = 1.

Определите свойства этого отношения на каждом из множеств:

р = . Изобразите граф отношения р и определите свойства. Будет ли отношение обладать каким-то дополнительным свойством, если в него добавить пару (5,8)?

• 145. Существует ли отношение, которое одновременно симметрично и антисимметрично?
• 146. Изобразите графы следующих отношений и определите их свойства:

• 147. Постройте пример бинарного отношения на множестве М=<а,Ь,с, которое симметрично, рефлексивно, но не транзитивно.
• 148. Если отношение р на множестве А симметрично, транзитивно и 0(р)=Л, то р рефлексивно. Докажите.
• 149. Приведите пример бинарного отношения на множестве М=<а_у 6, с>, которое транзитивно, но не симметрично и не антисимметрично.
• 150. Проанализируйте свойства приведенных отношений, заданных на множестве А:
  • а) А = N, отношение: 1) «х — делитель у»,
• 2) «х в два раза больше .у»,
• 3) «Числа л- и у взаимно простые».
• б) А = R + , отношение: 1) а=Ь 2 ,
• 2) a=kb для некоторого кеN.
• в) А — любое множество, отношение: 1) |х| = [у|. Докажите, что р отношение эквивалентности. Какое разбиение на классы

  эквивалентности порождает данное отношение?

  Рассмотрим отношение р на произвольном числовом множестве А: хру «х+у — целое четное число». Докажите, что р есть отношение эквивалентности. Постройте разбиение на классы, если

  • а) А =, б) А — множество всех целых чисел.
  • 11а множестве R задано отношение: хру«(х-у) — целое число». Докажите, что р есть отношение эквивалентности. Запишите классы эквивалентности, порожденные числами 5; 0,2; (-1,5). Что

  представляет собой геометрически класс эквивалентности,

  порожденный числом л?

  На множестве А = <xeZ 0 «Числа х и у имеют в десятичной записи одно и то же число цифр». Докажите, что р — отношение эквивалентности. Что представляют собой классы эквивалентности р? Сколько их?

  • 156. На множестве Z определены два отношения р и ст: хру«д: иу дают одинаковые остатки при делении на 4»;хсуу «Разность х-у делится на 4». Докажите, ч то отношения р и а совпадают, то есть числа д- и у находятся в отношении р тогда и только тогда, когда х и у находятся в отношении а. Докажите, что ото отношение есть отношение эквивалентности. На какие классы разбивается множество Z?
  • 157. Какое возможно обобщение предыдущей задачи?
  • 158. На множестве Z определено отношение: хру «Сумма х+у делится на 3». Является ли р отношением эквивалентности?
  • 159. Пусть/- функция из А в В. Определим на множестве А отношение: хру /(д) =/(v). Докажите, что р есть отношение эквивалентности. Что представляю! собой классы эквивалентности, если А

  

  • 160. Пусть на множестве А задано отношение эквивалентности р. Докажите критерий равенства классов эквивалентности: классы, порожденные элементами а и /?, равны тогда и только тогда, когда а находится в отношении р с /?.
  • 161. Используя результат предыдущей задачи, докажите, что никакие два различных класса эквивалентности не пересекаются. Рассуждения можно провести методом от противного.
  • 162. На множестве А =[3] задано отношение включения с. Постройте граф отношения. Найдите все пары несравнимых элементов.
  • 163. Пусть дано упорядоченное множество 1 функцией? Рассмотрите случаи:

  • 165. Пусть А = 4>. Укажите множество В, такое, чтобы отношение р, заданное правилом из предыдущей задачи, являлось взаимно однозначным соответствием между Л и В.
  • 166. Пусть А — множество окружностей на плоскости, В — множество точек этой плоскости. Между множествами А и В задано отношение/

  

  Является ли /функцией с областью определения А? Является ли это соответствие взаимно однозначным?

  167. Является ли отношение, заданное формулой^ = (-1) г • , .veN, >’gZ,

  взаимно однозначным соответствием между множествами N и Z? Через [я] обозначается целая часть числа а, то есть наибольшее целое число, не превосходящее а.

  🎥 Видео

  Математика 2 класс. «Множества и операции над ними»Скачать

  

  Выписать подмножества множестваСкачать

  

  Математика 2 класс. «Множества. Знаки ∈ и ∉ Объединение множеств и разделение на части»Скачать

  

  Множества ( 6 класс )Скачать

  

  Пересечение множеств Объединение множествСкачать

  

  Урок 48. Множество Элементы множества Пустое множество (6 класс)Скачать

  

  Дискретная математика. Лекция 1: Множества и отношенияСкачать