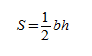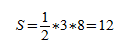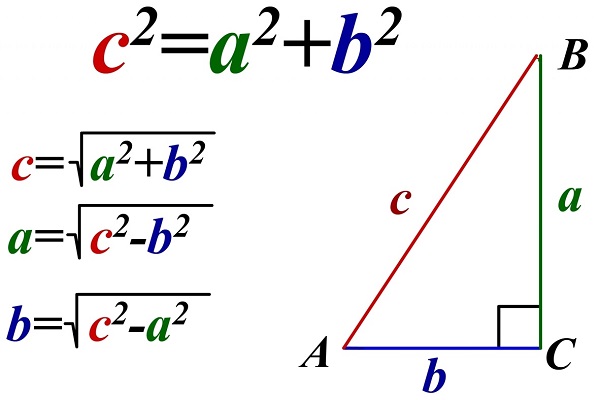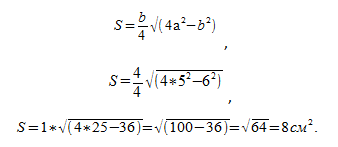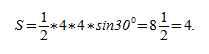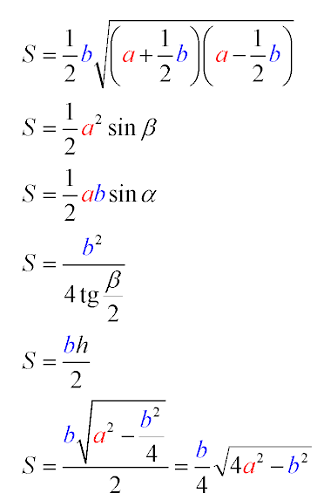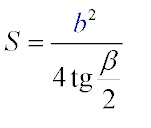S равнобедренного треугольника через синус

Площадь равнобедренного треугольника важна для вычисления многих геометрических и математических задач. Например, определение площади любого многоугольника связано с его разделением на ряд треугольников и расчетом площади каждого из них.

Геометрическое тело, обладающее двумя равными сторонами и углами – есть частный случай простого разностороннего многоугольника.

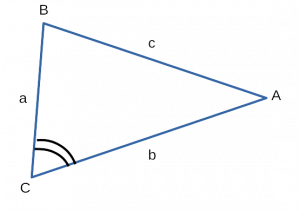
Каждая из идентичных линий называется боковой, а третья – основанием.

Если в таком треугольнике опустить среднюю линию из его вершины на 3-ю сторону, то образовавшиеся два плоских тела будут идентичны (так как имеют все признаки подобия).

Площадь (S) фигуры с тремя углами возможно установить:

по двум сторонам и высоте;

через угол между двумя сторонами и величину одной из них;

по двум сторонам;

через синус противолежащего основанию угла;

зная синус прилежащего угла и др.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

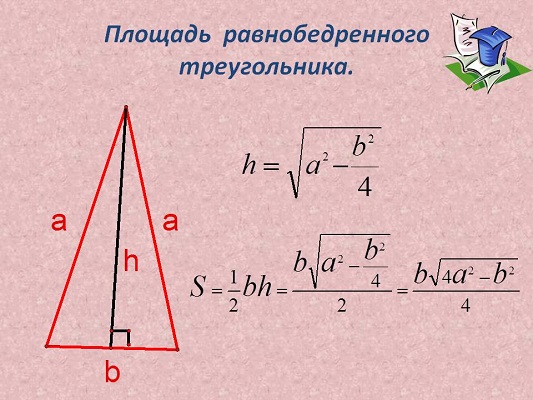
Площадь равнобедренного треугольника через высоту

Вычисление площади треугольника с использованием его высоты и параметров основания – самый актуальный вариант, на базе которого строятся многие другие методы решения.

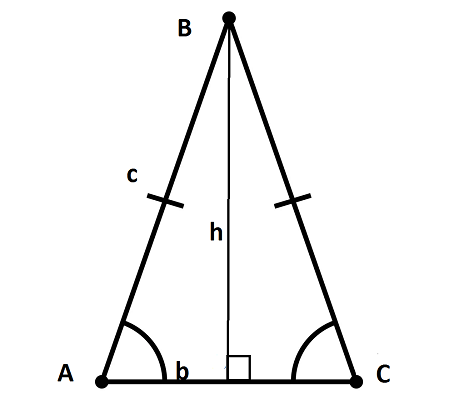
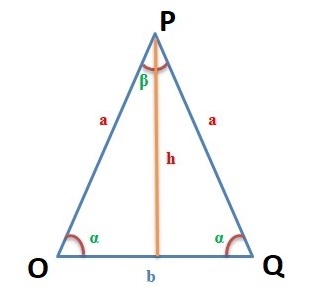
У планиметрической фигуры с двумя тождественными углами и боковыми отрезками высота может рассматриваться, как медиана и биссектриса. То есть линия, проведенная из вершины, делит планиметрический объект на два эквивалентных прямоугольных треугольника.

И общая их площадь сводится к:

b — размер основания;

Требуется рассчитать S тупоугольного равнобедренного многоугольника. Его h=3 см, а длина b = 8 см.

Вычисления выглядят следующим образом:

Видео:Вывод синуса двойного угла через площадь равнобедренного треугольника #егэ2024Скачать

Площадь равнобедренного треугольника через стороны

Найти S планиметрического тела с двумя одинаковыми чертами, зная их параметры, возможно.

Для этого необходима теорема Пифагора, формулы которой видны на картинке,

и формула для отыскания S через биссектрису S = ½ * b * h.

После проведения медианы к середине 3-его отрезка, в равнобедренном треугольнике образуются 2 единообразных плоских тела с h между 2-мя катетами.

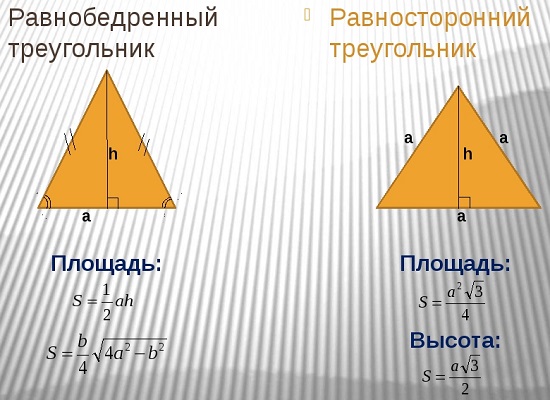
Таким образом, используя свойство сторон прямоугольного треугольника, выводим формулу, которая показана на картинке:

При высчитывание S равностороннего треугольника это выражение примет другой вид. Сравнить формулы нахождения площади равностороннего и равнобедренного треугольников можно, взглянув на картинку:

У остроугольного равнобедренного треугольника даны габариты боковины b = 3 см и базиса a = 2 см. Надлежит найти его S:

Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Площадь равнобедренного треугольника через синус угла

В геометрии встречаются задания по отысканию площади многоугольника с тремя схожими краями через данный угол и длину прилегающей стороны.

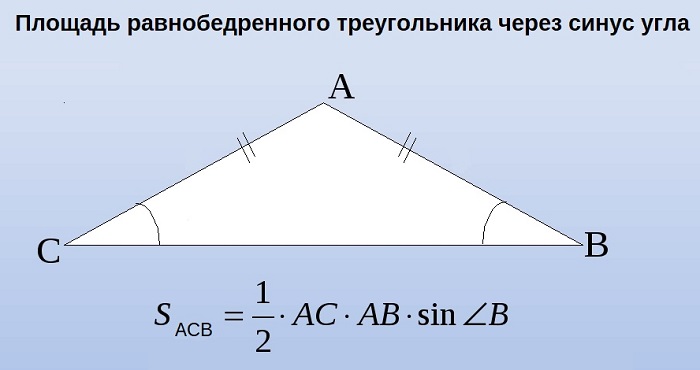
В этой ситуации определение размера h будет осуществляться с использованием угла, прилегающего к измеренной грани. Таким образом выводится выражение, которое хорошо иллюстрирует следующая картинка:

Посмотрим на рисунок, приведенный выше. Известно, что ∠ACB фигуры 30 градусов, а величина его боковой стороны AC = AB равняется 4 см. Требуется вычислить её S.

Видео:Площадь равнобедренного треугольникаСкачать

Формула площади равнобедренного треугольника через тангенс угла

Как правило, в планиметрии нередко встречаются задания по нахождению S треугольника, в котором определено значение стороны и угол.

Разнообразные равенства для решения задач, в том числе и нахождения S через тангенс угла, можно увидеть ниже:

Дан равнобедренный треугольник OPQ (см. рис. 1). Известны величины: основание OQ = 5 см и угол QOP = 45 0 . Требуется найти площадь треугольника OPQ.

Прежде всего посмотрим, как найти нам требуемую величину и какую применить формулу. Остановим свой выбор на формуле нахождения площади S по тангенсу угла.

Зная, что у нас равнобедренный треугольник, у которого углы у основания равны, найдем третий угол:

180 — 45 — 45 = 90 0 — угол OPQ.

S_OPQ = 5 2 /4 * tg 45° = 25/4 * 1 = 6, 25 см 2

Вот так, используя прежде всего знания о свойствах фигур, можно получать самые разнообразные способы вычисления той величины, какая требуется в задаче.

Видео:ВЫСОТА через СИНУС / равнобедренный треугольник / #планиметрия #27327Скачать

Как найти площадь треугольника

На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.

Треугольник – это многоугольник с тремя сторонами.

По формуле Герона

Формула Герона для нахождения площади треугольника:

Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:

Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:

Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

Площадь прямоугольного треугольника

Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.

Формула нахождения площади прямоугольного треугольника через катеты:

Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.

Формула нахождения площади равнобедренного треугольника через две стороны:

Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:

Площадь равностороннего треугольника через стороны

Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.

Формула нахождения площади равностороннего треугольника через сторону:

Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:

Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Площадь треугольника через синус

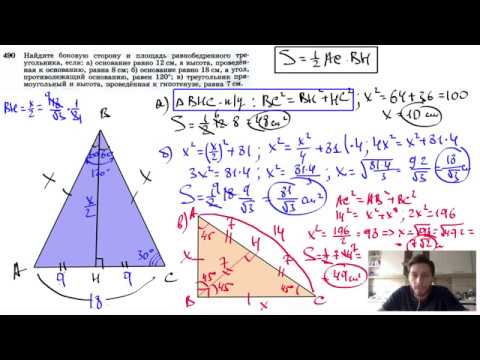
Видео:№490. Найдите боковую сторону и площадь равнобедренного треугольника, если: а) основание равноСкачать

Определение

Площадь треугольника через синус — это площадь треугольника,
выраженная через две любые стороны треугольника и синус угла между ними.

Синус угла — это число, которое используется для нахождения
разных величин в треугольниках, его можно найти в специальных таблицах.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Введение

Площадь треугольника кроме половины произведения высоты
на основания, можно также найти и другим способом.
Мало кто знает, но через синусы углов можно найти обычно
не только стороны, но и площадь любого треугольника!

Площадь треугольника выраженная без синуса численно равна
половине произведения двух сторон друг на друга
на синус угла между ними.

Площадь треугольника через синус ищется только в том случае,
если по другой формуле площадь треугольника найти нельзя.

Теорема

( S = frac2 * BC * AC * sin angle BCA ) ​

Площадь произвольного треугольника равна полусумме
произведения двух любых сторон треугольника друг на друга,
и на синус угла между этими сторонами.

Формула

[ S = frac2 * a * b * sin α ]

Где a, b — две стороны треугольника, синус α — синус угла α.

Пример

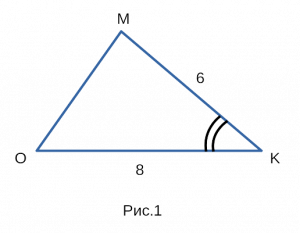
Для примера, возьмем треугольник omk, изображенный на рисунке 1, со сторонами om, mk, ok.
Известно, что mk равен 6, ok равен 8, синус угла okm равен 1/4.

Нужно найти площадь треугольника omk.

Дано: △omk, mk = 6, ok = 8, sin okm = 1/4.

Найти: S △omk — ?

Решение:

1) ​ ( S = frac2*a*b*sin α ) ​​ ( implies ) ​ ( S = frac2*mk*ok*sin okm ) ​

2) S = 1/2 * 6 * 8 * 1/4 = 1/2 * 6 * 8 * 0.25 = 1/2 * 48 * 0.25 = 1/2 * 12 = 6

Ответ: Площадь треугольника omk равна 6.

Доказательство

Докажем, что площадь произвольного треугольника
равна полусумме произведения двух любых сторон
друг на друга, и на синус угла между этими сторонами.

Чтобы вам наглядно было видно, как мы доказываем,
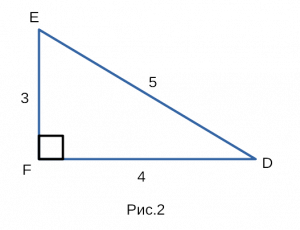
используем один из известнейших треугольников — египетский треугольник.
Высота в египетском треугольнике равна длине одного из катетов.
Построим прямоугольный треугольник, изображенный на рисунке 2,
со сторонами 3,4,5 с одним из углов 90 градусов.

Первым делом найдем площадь обычной формулой,
затем с помощью синуса. Площадь равна половине
основания на высоту — ½3*4 = 6. Теперь найдем с
помощью синуса: ½3*4*sin90 = 6 * 1 = 6. Как видим,
полученные значения площадей сходятся, соответственно
через синус можно найти площадь треугольника ч.т.д.

Теперь, чтобы найти площадь треугольника нам не нужно
знать основание и высоту, можно знать только
две стороны и синус угла между ними.

Видео:№598. Найдите площадь равнобедренного треугольника с углом а при основании, еслиСкачать

Заключение

В заключение, можно сказать, что площадь
треугольника можно найти разными способами.
Например, в прямоугольном треугольнике площадь
рассчитать легче чем в любом другом треугольнике,
так как высота уже известна. Именно поэтому,
в школьном курсе, отчасти так подробно изучаются
прямоугольные треугольники. В Древнем Египте были
распространены прямоугольные треугольники со
сторонами 3,4,5; 6,8,10; 5,12,13. Длины этих прямоугольных
треугольников треугольников целые, что значительно,
упрощало разного рода вычисления.

Формулу площади треугольника делает универсальной то,
что она может применена к абсолютно любым треугольникам.
Главное, чтобы были известные две стороны,
и угол или синус угла между ними.

Формула площади треугольника через синус — универсальна,
поэтому может быть применена к любым видам треугольников.

📺 Видео

Площадь равнобедренного треугольника для фанатов Dark Souls и для всех остальных #огэ2023 #егэ2023Скачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Площадь равнобедренного треугольника равна √3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Площадь равнобедренного треугольникаСкачать

Найдите площадь равнобедренного треугольника, основание которого равно 12 см, а боковая сторона 10.Скачать

ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Площадь треугольника по полупроизведению сторон на синус угла между нимиСкачать

Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора | Геометрия | АлгебраСкачать

16 заание ОГЭ . 16.3.4. Равнобедренные треугольникиСкачать

✓ Новая формула площади треугольника | Ботай со мной #108 | Борис ТрушинСкачать

8 класс, 14 урок, Площадь треугольникаСкачать