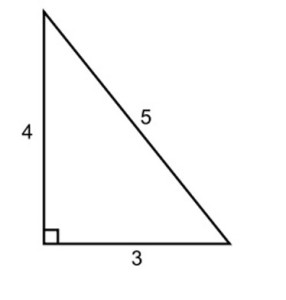
Египетский треугольник – прямоугольный треугольник с отношением сторон 3:4:5. Это наиболее простой из треугольников, стороны и площади которых выражаются целыми числами. Он представляет собой прекрасную иллюстрацию теоремы Пифагора – действительно, квадрат его гипотенузы (25) очевидно равен сумме квадратов его катетов (9 и 16). Предполагается даже, что именно знакомство с египетским треугольником сподвигло Пифагора на формулировку его теоремы. Впрочем, как всегда в подобных случаях, историки древности, которые не являются специалистами ни в одной другой области знания, кроме истории (и уж точно плохо смыслят в математике), могут ошибаться.
Так или иначе, имеются многочисленные указания на то, что теорема Пифагора вообще и египетский треугольник в частности были известны и широко использовались за много веков до Пифагора и далеко за пределами Египта – в Месопотамии, в долине Инда, в древнем Китае. И вправду, корень многих знаний следует искать, наверное, в практической деятельности человека. Как только возникла необходимость возводить здания и сооружения, человек эмпирическим путём пришёл к пониманию важности прямых углов. А как отмерить прямой угол, не имея геодезических приборов?
Оказывается, очень просто. Берём верёвку и делим её на 12 равных частей – например, при помощи складывания. Выбираем отрезок верёвки, равный 5, так, чтобы он находился межды двумя другими, равными 3 и 4. Выпрямляем его и фиксируем на ровном участке земли при помощи двух колышков. А затем натягиваем концы верёвки и сводим их в одну точку, чтобы получился треугольник. Прямоугольный, египетский.
«Делай, как делается». Знаменитая древнеегипетская пословица, дошедшая до наших дней. У нас её обычно понимают, как мудрое наблюдение: если так получается, значит, так правильно. Но при этом часто забывают культурно-исторический контекст Древнего Египта. Всеми работами руководили жрецы – члены замкнутой касты харнителей священного, древнего знания. Поэтому «делай, как делается» в древнеегипетском контексте наверняка значило «делай как говорят и не задавай лишних вопросов». То есть жрецы знали не только, «как» делать, чтобы «делалось», но и «почему», и это зание было скрыто от непосвящённых.
Мы тоже хотим знать, «почему». Нам недостаточно «как». Человеческий ум будоражат разнообразные загадки, и так, наверное, будет всегда. Египетский треугольник, хоть и известен с незапамятных времён – одна из таких загадок.
Начнём с того, что он красив. Его форма проста и гармонична, на него приятно смотреть. И с ним легко работать, используя самые простые инструменты – линейку и циркуль. Он, казалось бы, даже приглашает поработать с ним. Что ж, примем приглашение и посмотрим, что у нас получится.
Несколько простых построений, в числе которых – квадраты гипотенузы и катетов, а также симметричные отображения, сразу дают нам красивые, грмоничные фигуры. Здесь мы видим и мальтийский крест, и серединное сечение пирамиды Хефрена, и фрактальный ряд убывающих (возрастающих) по размерам египетских треугольников в соответствии с правилом золотого сечения. Удивительное богатство гармоничных пропорций. И кажется, что ещё немного, и неразрешимая задача о квадратуре круга будет решена.
Впрочем, не станем уподобляться безумцам, которые изобретают вечный двигатель, ищут квадратуру круга, философский камень и книгу мёртвых. Ограничимся констатацией бесконечных возможностей создания красоты и гармонии при помощи простой верёвки, разделённой на 12 равных частей. В том числе и картины в стиле арифмизма. Картины, которая, в соответствии с определением, изображает законченное арифметическое выражение: 9 + 16 = 25. Математический и геометрический смысл очевиден. Тайное значение – наверное, на то оно и тайное, чтобы таковым оставаться. А многозначительная и почти мистическая эстетика данных форм пусть радует глаз и будоражит воображение.
Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Интегрированный урок по теме: «Египетские треугольник». 8-й класс
Класс: 8
Цели:
Оборудование урока: портрет Пифагора, проектор с экраном, веревка с 12 узлами, компьютеры.
I. Организационный момент, где учитель сообщает тему урока и его цели.
II. Проверка домашнего задания
А) Один ученик доказывает теорему Пифагора у доски.
Б) Ответы на вопросы:
1. Сформулируйте теорему Пифагора.
2. Какой треугольник называется прямоугольным?
3. Как называются стороны прямоугольного треугольника?
4. Заслушивание доклада учащегося “Теорема Пифагора”
5. Заслушивание доказательства теоремы Пифагора.
В) Решение задач по готовым чертежам.
Г) Составление алгоритма решения задачи.
1. Нахождение прямоугольного треугольника.
2. Запись теоремы Пифагора к конкретной задаче.
3. Составление и решение уравнения.
Д) Вывешивается таблица алгоритма.
1. Найти с.
2. с 2 = а 2 + в 2
3. с 2 = 8 2 + 6 2
III. Изучение нового материала.
А) Историческая справка.
Землемеры Древнего Египта для построения прямого угла использовали бечевку, разделенную узлами на 12 равных частей, покажите, как они это делали. (К доске вызываются 3 желающих продемонстрировать построение прямоугольного треугольника). Напоминаю, что в углах должны быть узлы. Ребята, выполнив с помощью веревки построение, очень довольны, что побывали в роли древних египтян. Рассказывают, что и сейчас при закладывании фундаментов новых домов очень часто строители используют именно этот способ построения прямых углов будущих домов.
Б) Постройте на компьютере треугольник АВС
Дано: а=4 см; в=3 см;
С=90 °
Решение: с 2 =а 2 +в 2
с1=5; с2=-5 постороннее решение, длина гипотенузы – положительное число.
В) Ответ проверьте измерениями.
Г) Как вы думаете, какое название носит этот прямоугольный треугольник?
Правильно, Египетский треугольник, так и тема нашего урока. Ребята, запишите в тетрадях тему урока «Египетский треугольник».
IV. Развитие умений и навыков.
А) Найдите сторону ромба, если его диагонали 8 см и 6см.
На экране с помощью проектора дается чертеж.
Дано: АВСД – ромб
Решение: устно составим алгоритм решения задачи.
1. 
2. АВ 2 =АО 2 +ВО 2 (АО = 
А как было проще решить, не выполняя вычислений, кто догадается?
Ответ: я вижу, что в прямоугольном треугольнике катеты равны 3 и 4, значит он Египетский, а поэтому гипотенуза равна 5, т.е. АВ=5.
Учитель: Вот ребята, оказывается не всегда нужно выполнять вычисления, а можно, зная определение Египетского треугольника, сразу дать ответ.
V. Работа в группах на 5–6 минут (класс разбит на несколько групп по 4 человека) каждая группа получает задание – карточку.
Стороны ромба равны по 13 см, а большая диагональ его равна 24 см. Вычислите другую диагональ.
В равнобокой трапеции основания равны 10 см и 40 см. Боковая сторона равна 25 см. Вычислите высоту трапеции.
В равнобедренной трапеции основания равны 7 см и 25 см, высота равна 12 см. Вычислите диагональ АС и периметр трапеции.
В прямоугольной трапеции основания равны 11 см и 20 см. Большая боковая сторона ее равна 41 см. Найдите периметр трапеции.
В прямоугольной трапеции АВ 

Быстрая проверка: на экране через проектор проецируется чертеж к 1 карточке и ребята рассказывают свое решение.
АО=
25 АЕ=FД=
ВЕ=

Ответ: 62.

Из 

Ответ: 112.
АВС, LВ=
, АВ=ВС=5



Ответ: 10.
VI. Задание на дом п.64, №17,18.
VII. Подведение итога урока, выставление оценок.
А) Возможно ли было решить задачи данного типа без знания теоремы Пифагора?
Б) О чем надо помнить, применяя теорему Пифагора?
В) Вспомните алгоритм решения задач данного типа.
Г) Достигли ли мы цели урока?
Д) Что вам понравилось на этом уроке?
Учитель благодарит всех за работу на уроке.
Литература:
- А.В. Погорелов. Учебник. Геометрия 7-11.
- Г.И. Глейзер, История математики в школе.
- В.К. Смышляев, О математике и математиках.
Видео:Египетский треугольникСкачать

Египетский треугольник
Автор: admin · 8 апреля, 2014
Видео:Египетский треугольник. Пифагоровы тройки.Скачать

Египетский треугольник.
Название «египетский треугольник» появилось уже в 5 веке до н.э. Принадлежит оно прямоугольному треугольнику, стороны которого равны соответственно 3, 4 и 5.
Назван он был так потому, что очень широко применялся еще в Древнем Египте в различных сферах жизнедеятельности.
Хотя уже тогда он был знаком людям далеко за пределами Древнего Египта, но, видимо, его уникальные свойства заметили и начали использовать впервые именно там.
В чем же состоит его отличительная особенность?
Во-первых, все его стороны и площадь — это целые числа;
во-вторых, сумма квадратов катетов равна квадрату гипотенузе ( а это ведь теорема Пифагора, которую все знают со школы! Но о Пифагоре чуть позже);
в-третьих, это то, что с его помощью можно отмерять прямые углы в пространстве (треугольник-то прямоугольный!), а это просто необходимо, например, в строительстве;
и, в-четвертых, этот треугольник можно запросто построить с помощью простой веревки.

А теперь про Пифагора. Египетский треугольник тесно связан с его именем.
Возможно, изучение интересных особенностей египетского треугольника и подтолкнуло Пифагора на попытку обобщения зависимостей во всех других прямоугольных треугольниках. Что ему, как известно, удалось!
Кстати, оказывается, теорема Пифагора попала в Книгу Рекордов Гиннеса как теорема с самым большим количеством доказательств (их насчитывается около 500).
📺 Видео
Что такое периметр. Как найти периметр многоугольника?Скачать

КАК НАЙТИ ПЕРИМЕТР ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать

Пифагоровы тройки 1. Египетский треугольникСкачать

Египетский треугольник #огэ #математика #shortsСкачать

Египетский треугольникСкачать

Как найти периметр?Скачать

Урок. Как найти периметр треугольника. Математика 2 класс. #учусьсамСкачать

Как найти периметр данной фигуры? Решение за одну минуту!Скачать

Что такое египетский треугольник?Скачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Математика 2 класс. «Периметр треугольника, прямоугольника и квадрата»Скачать

Египетский треугольникСкачать

Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

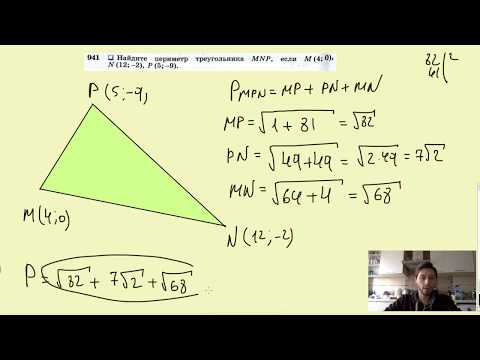
№941. Найдите периметр треугольника MNP, если М (4; 0), N(12; -2), В (5; -9).Скачать
Задача, которую исключили из экзамена в АмерикеСкачать

Построение египетского треугольника.Скачать

Задачи на периметр труегольника. Геометрия 7 класс. Две задачи.Скачать


 С=90 °
С=90 °