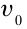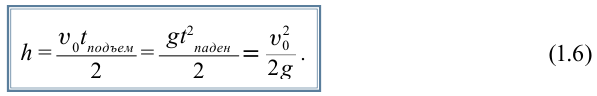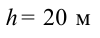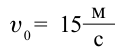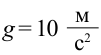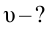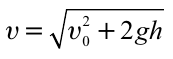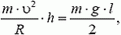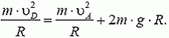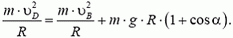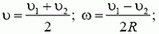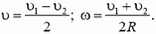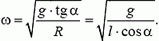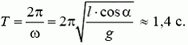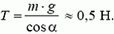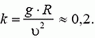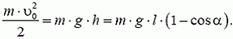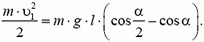Вертикальное движение тел:
Если держать в руках какой-либо предмет, а затем отпустить его, то предмет из-за притяжения Земли начнет двигаться прямо к ее поверхности. Такое движение тел называется вертикальное движение вниз. С этим движением вы ознакомились на уроках физики в 7 классе. В этой теме мы рассмотрим вертикальное движение вниз с точки зрения принципа независимости движений.
Когда тело двигается вертикально, на него действует одна или несколько сил (сила тяжести, сила сопротивления воздуха, сила Архимеда). В случае движения тел вверх (вертикально) в целях упрощения задачи мы не учитываем силу сопротивления воздуха и силу Архимеда.
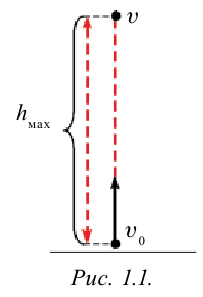
Понаблюдаем за движением какого-либо предмета, подбросив его вверх в вертикальном направлении (рис. 1.1.). Если бы тело двигалось вверх только со скоростью
Движение тела, брошенного вертикально вверх, является равнозамедленным движением.
Скорость тела через время 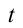
Тело останавливается при достижении самой верхней точки 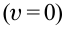
Приравнивая левую сторону выражения (1.4) нулю, находим выражение для определения времени, необходимого для подъема тела:
Максимальная высота подъема тела определяется выражением:
В условиях, когда сопротивление воздуха ничтожно мало и можно его не учитывать, время подъема брошенного вверх тела будет равно времени падения вниз 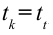
Тело, брошенное вертикально вниз, совершает равномерно ускоренное движение. Здесь скорость тела через время 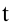
Уравнение движения тела, брошенного вертикально вниз, запишем следующим образом:
Первым закономерности вертикального движения тел экспериментальным способом начал изучать великий итальянский ученый Г. Галилей. На основе проведенных опытов были обнаружены две закономерности вертикального падения тел. Во-первых, вертикальное падение тела является прямолинейным равноускоренным движением, во-вторых, все тела при свободном падении двигаются с постоянным ускорением.
Если учесть, что свободное падение тел является равноускоренным движением, то все уравнения прямолинейного равноускоренного движения в этом случае также действительны, т.е. можно заменить ускорение 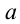
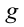
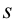
Из-за того, что свободное падение происходит равноускоренно, а движение вертикально вверх – равнозамедленно, среднюю скорость движения тела можно определить из следующего выражения:
Образец решения задачи:
Начальная скорость предмета, падающего с крыши здания высотой
20 м, равна 15 м/сек. Чему равняется его скорость в момент столкновения
с землей?
Решение: 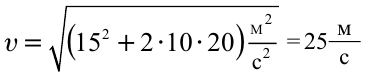
Ответ:
| Уравнения равноускоренного движения | Уравнения движения при свободном падении |
|---|---|
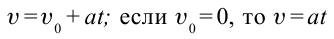 | 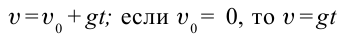 |
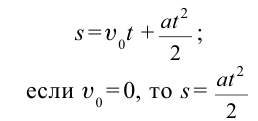 | 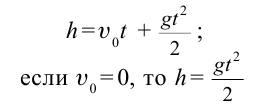 |
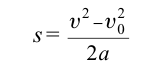 | 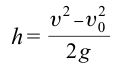 |
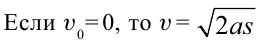 | 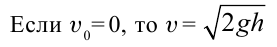 |
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Неравномерное движение по окружности
- Равномерное движение по окружности
- Взаимная передача вращательного и поступательного движения
- Движение горизонтально брошенного тела
- Опыты Фарадея в физике
- Электромагниты и их применение в физике
- Колебательный контур в физике
- Исследовательские методы в физике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Движение тела, брошенного вертикально вверх. Невесомость | Физика 9 класс #14 | ИнфоурокСкачать

Движение по окружности
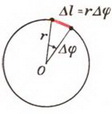
Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .
Видео:Физика - движение по окружностиСкачать

Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости — радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Видео:Теория движение тела брошенного вертикально вверхСкачать

Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → — радиус вектор точки на окружности с началом в ее центре.
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
Видео:Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

Асламазов Л.Г. Движение по окружности // Квант
Асламазов Л.Г. Движение по окружности // Квант. — 1972. — № 9. — С. 51-57.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Для описания движения по окружности наряду с линейной скоростью вводят понятие угловой скорости. Если точка при движении по окружности за время Δt описывает дугу, угловая мера которой Δφ, то угловая скорость 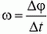
Угловая скорость ω связана с линейной скоростью υ соотношением υ = ω·r, где r — радиус окружности, по которой движется точка (рис. 1). Понятие угловой скорости особенно удобно для описания вращения твердого тела вокруг оси. Хотя линейные скорости у точек, находящихся на разном расстоянии от оси, будут неодинаковыми, их угловые скорости будут равны, и можно говорить об угловой скорости вращения тела в целом.
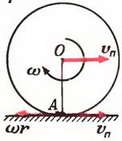
Задача 1. Диск радиуса r катится без проскальзывания по горизонтальной плоскости. Скорость центра диска постоянная и равна υп. С какой угловой скоростью при этом вращается диск?
Каждая точка диска участвует в двух движениях — в поступательном движении со скоростью υп вместе с центром диска и во вращательном движении вокруг центра с некоторой угловой скоростью ω.
Для нахождения ω воспользуемся отсутствием проскальзывания, то есть тем, что в каждый момент времени скорость точки диска, соприкасающейся с плоскостью, равна нулю. Это означает, что для точки А (рис. 2) скорость поступательного движения υп равна по величине и противоположна по направлению линейной скорости вращательного движения υвр = ω·r. Отсюда сразу получаем 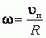
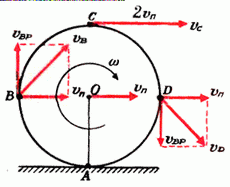
Задача 2. Найти скорости точек В, С и D того же диска (рис. 3).
Рассмотрим вначале точку В. Линейная скорость ее вращательного движения направлена вертикально вверх и равна 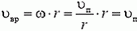
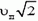
Даже в том случае, когда скорость точки, движущейся по окружности, не меняется по величине, точка имеет некоторое ускорение, так как меняется направление вектора скорости. Это ускорение называется центростремительным. Оно направлено к центру окружности и равно 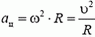
Если же скорость точки, движущейся по окружности, меняется не только по направлению, но и по величине, то наряду с центростремительным ускорением существует и так называемое тангенциальное ускорение. Оно направлено по касательной к окружности и равно отношению 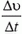
Задача 3. Найти ускорения точек А, В, С и D диска радиуса r, катящегося без проскальзывания по горизонтальной плоскости. Скорость центра диска постоянна и равна υп (рис. 3).
В системе координат, связанной с центром диска, диск вращается с угловой скоростью ω, а плоскость движется поступательно со скоростью υп. Проскальзывание между диском и плоскостью отсутствует, следовательно, 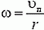
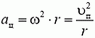
Перейдем теперь к задачам на динамику вращательного движения. Вначале рассмотрим простейший случай, когда движение по окружности происходит с постоянной скоростью. Так как ускорение тела при этом направлено к центру, то и векторная сумма всех сил, приложенных к телу, должна быть тоже направлена к центру, и по II закону Ньютона 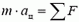
Следует помнить, что в правую часть этого уравнения входят только реальные силы, действующие на данное тело со стороны других тел. Никакой центростремительной силы при движении по окружности не возникает. Этим термином пользуются просто для обозначения равнодействующей сил, приложенных к телу, движущемуся по окружности. Что касается центробежной силы, то она возникает только при описании движения по окружности в неинерциальной (вращающейся) системе координат. Мы пользоваться здесь понятием центростремительной и центробежной силы вообще не будем.
Задача 4. Определить наименьший радиус закругления дороги, которое автомобиль может пройти при скорости υ = 70 км/ч и коэффициенте трения шин о дорогу k =0,3.
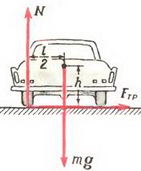
На автомобиль действуют сила тяжести Р = m·g, сила реакции дороги N и сила трения Fтp между шинами автомобиля и дорогой. Силы Р и N направлены вертикально и равны по величине: P = N. Сила трения, препятствующая проскальзыванию («заносу») автомобиля, направлена к центру поворота и сообщает центростремительное ускорение: 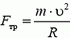
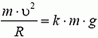
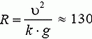
Сила реакции дороги N при движении автомобиля по окружности не проходит через центр тяжести автомобиля. Это связано с тем, что ее момент относительно центра тяжести должен компенсировать момент силы трения, стремящийся опрокинуть автомобиль. Величина силы трения тем больше, чем больше скорость автомобиля 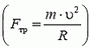
Задача 5. При какой скорости автомобиль, движущийся по дуге окружности радиуса R = 130 м, может опрокинуться? Центр тяжести автомобиля находится на высоте h = 1 м над дорогой, ширина следа автомобиля l = 1,5 м (рис. 4).
В момент опрокидывания автомобиля как сила реакции дороги N, так и сила трения Fтp приложены к «внешнему» колесу. При движении автомобиля по окружности со скоростью υ на него действует сила трения 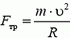
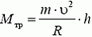
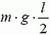
Откуда 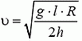
Чтобы автомобиль мог двигаться с такой скоростью, необходим коэффициент трения 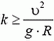
Аналогичная ситуация возникает при повороте мотоцикла или велосипеда. Сила трения, создающая центростремительное ускорение, имеет момент относительно центра тяжести, стремящийся опрокинуть мотоцикл. Поэтому для компенсации этого момента моментом силы реакции дороги мотоциклист наклоняется в сторону поворота (рис. 5).
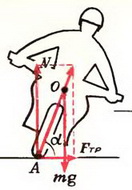
Задача 6. Мотоциклист едет по горизонтальной дороге со скоростью υ = 70 км/ч, делая поворот радиусом R = 100 м. На какой угол α к горизонту он должен при этом наклониться, чтобы не упасть?
Сила трения между мотоциклом и дорогой 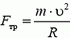
Подставляя сюда значения Fтp и N, находим что 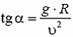
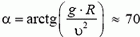
Для того, чтобы увеличить скорость движения по закруглению дороги, участок дороги на повороте делают наклонным. При этом в создании центростремительного ускорения, кроме силы трения, участвует и сила реакции дороги.
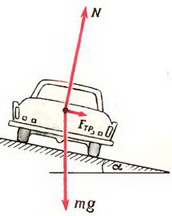
Задача 7. С какой максимальной скоростью υ может двигаться автомобиль по наклонному треку с углом наклона α при радиусе закругления R и коэффициенте трения шин о дорогу k?
На автомобиль действуют сила тяжести m·g, сила реакции N, направленная перпендикулярно плоскости трека, и сила трения Fтp, направленная вдоль трека (рис. 6).
Так как нас не интересуют в данном случае моменты сил, действующих на автомобиль, мы нарисовали все силы приложенными к центру тяжести автомобиля. Векторная сумма всех сил должна быть направлена к центру окружности, по которой движется автомобиль, и сообщать ему центростремительное ускорение. Поэтому сумма проекций сил на направление к центру (горизонтальное направление) равна 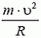
Сумма проекций всех сил на вертикальное направление равна нулю:
Подставляя в эти уравнения максимальное возможное значение силы трения Fтp = k·N и исключая силу N, находим максимальную скорость 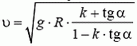
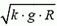
Разобравшись с динамикой поворота, перейдем к задачам на вращательное движение в вертикальной плоскости.
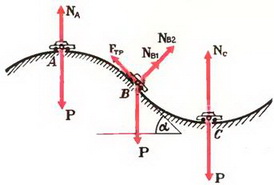
Задача 8. Автомобиль массы m = 1,5 т движется со скоростью υ = 70 км/ч по дороге, показанной на рисунке 7. Участки дороги АВ и ВС можно считать дугами окружностей радиуса R = 200 м, касающимися друг друга в точке В. Определить силу давления автомобиля на дорогу в точках А и С. Как меняется сила давления при прохождении автомобилем точки В?
В точке А на автомобиль действуют сила тяжести Р = m·g и сила реакции дороги NA. Векторная сумма этих сил должна быть направлена к центру окружности, то есть вертикально вниз, и создавать центростремительное ускорение: 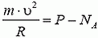
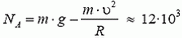
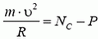
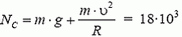
В точке В автомобиль переходит с выпуклого участка дороги на вогнутый (или наоборот). При движении по выпуклому участку проекция силы тяжести на направление к центру должна превышать силу реакции дороги NB1, причем 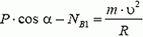

Из этих уравнений получаем, что при прохождении точки В сила давления автомобиля на дорогу меняется скачком на величину 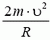
При движении автомобиля по окружности с постоянной скоростью сумма проекций всех сил на направление, касательное к окружности, должна быть равна нулю. В нашем случае касательная составляющая силы тяжести уравновешивается силой трения между колесами автомобиля и дорогой.
Величина силы трения регулируется вращательным моментом, прикладываемым к колесам со стороны мотора. Этот момент стремится вызвать проскальзывание колес относительно дороги. Поэтому возникает сила трения, препятствующая проскальзыванию и пропорциональная приложенному моменту. Максимальное значение силы трения равно k·N, где k — коэффициент трения между шинами автомобиля и дорогой, N — сила давления на дорогу. При движении автомобиля вниз сила трения играет роль тормозящей силы, а при движении вверх, наоборот, роль силы тяги.
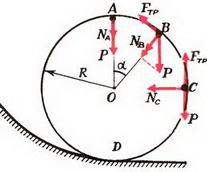
Задача 9. Автомобиль массой m = 0,5 т, движущийся со скоростью υ = 200 км/ч, совершает «мертвую петлю» радиуса R = 100 м (рис. 8). Определить силу давления автомобиля на дорогу в верхней точке петли А; в точке В, радиус-вектор которой составляет угол α = 30º с вертикалью; в точке С, в которой скорость автомобиля направлена вертикально. Возможно ли движение автомобиля по петле с такой постоянной скоростью при коэффициенте трения шин о дорогу k = 0,5?
В верхней точке петли сила тяжести и сила реакции дороги NA направлены вертикально вниз. Сумма этих сил создает центростремительное ускорение: 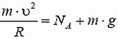
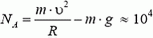
Сила давления автомобиля на дорогу равна по величине и противоположна по направлению силе NА.
В точке В центростремительное ускорение создается суммой силы реакции и проекции силы тяжести на направление к центру: 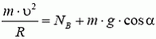
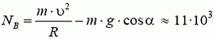
Легко видеть, что NB > NA; с увеличением угла α сила реакции дороги увеличивается.
В точке С сила реакции 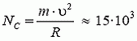
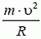
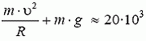
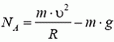
Скорость автомобиля будет постоянной, если касательная составляющая силы тяжести не превышает максимальной силы трения k·N во всех точках петли. Это условие заведомо выполняется, если минимальное значение 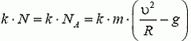
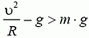
Таким образом, в нашем случае движение автомобиля по «мертвой петле» с постоянной скоростью возможно.
Рассмотрим теперь движение автомобиля по «мертвой петле» с выключенным мотором. Как уже отмечалось, обычно момент силы трения противодействует моменту, приложенному к колесам со стороны мотора. При движении автомобиля с выключенным мотором этого момента нет, и силой трения между колесами автомобиля и дорогой можно пренебречь.
Скорость автомобиля уже не будет постоянной — касательная составляющая силы тяжести замедляет или ускоряет движение автомобиля по «мертвой петле». Центростремительное ускорение тоже будет меняться. Создается оно, как обычно, равнодействующей силы реакции дороги и проекции силы тяжести на направление к центру петли.
Задача 10. Какую наименьшую скорость должен иметь автомобиль в нижней точке петли D (см. рис. 8) для того, чтобы совершить ее с выключенным мотором? Чему будет равна при этом сила давления автомобиля на дорогу в точке В? Радиус петли R = 100 м, масса автомобиля m = 0,5 т.
Посмотрим, какую минимальную скорость может иметь автомобиль в верхней точке петли А, чтобы продолжать двигаться по окружности?
Центростремительное ускорение в этой точке дороги создается суммой силы тяжести и силы реакции дороги 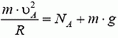



Теперь определим, какую скорость должен иметь автомобиль в нижней точке петли D, чтобы в верхней точке петли А его скорость 
Приравняем значения энергии автомобиля в точках А и D. При этом будем отсчитывать высоту от уровня точки D, то есть потенциальную энергию автомобиля в этой точке будем считать равной нулю. Тогда получаем
Подставляя сюда значение 
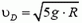
Если автомобиль въедет в петлю с такой скоростью, то он сможет совершить ее с выключенным мотором.
Определим теперь, с какой силой при этом автомобиль будет давить на дорогу в точке В. Скорость автомобиля в точке В опять легко находится из закона сохранения энергии:
Подставляя сюда значение 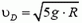

Воспользовавшись решением предыдущей задачи, по заданной скорости находим силу давления в точке B:
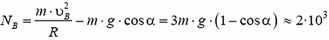
Аналогично можно найти силу давления в любой другой точке «мертвой петли».
1. Найти угловую скорость искусственного спутника Земли, вращающегося по круговой орбите с периодом обращения Т = 88 мин. Найти линейную скорость движения этого спутника, если известно, что его орбита расположена на расстоянии R = 200 км от поверхности Земли.
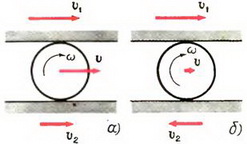
2. Диск радиуса R помещен между двумя параллельными рейками. Рейки движутся со скоростями υ1 и υ2. Определить угловую скорость вращения диска и скорость его центра. Проскальзывание отсутствует.
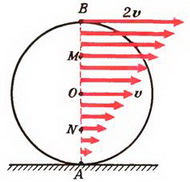
3. Диск катится по горизонтальной поверхности без проскальзывания. Показать, что концы векторов скоростей точек вертикального диаметра находятся на одной прямой.
4. Самолет движется по окружности с постоянной горизонтальной скоростью υ = 700 км/час. Определить радиус R этой окружности, если корпус самолета наклонен на угол α = 5°.
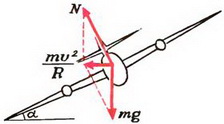
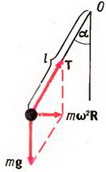
5. Груз массы m = 100 г, подвешенный на нити длины l = 1 м, равномерно вращается по кругу в горизонтальной плоскости. Найти период обращения груза, если при его вращении нить отклонена по вертикали на угол α = 30°. Определить также натяжение нити.
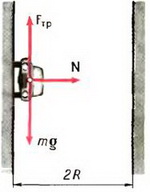
6. Автомобиль движется со скоростью υ = 80 км/ч по внутренней поверхности вертикального цилиндра радиуса R = 10 м по горизонтальному кругу. При каком минимальном коэффициенте трения между шинами автомобиля и поверхностью цилиндра это возможно?
7. Груз массой m подвешен на нерастяжимой нити, максимально возможное натяжение которой равно 1,5m·g. На какой максимальный угол α можно отклонить нить от вертикали, чтобы при дальнейшем движении груза нить не оборвалась? Чему будет равно при этом натяжение нити в тот момент, когда нить составит угол α/2 с вертикалью?
I. Угловая скорость искусственного спутника Земли 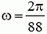
2. Здесь возможны два случая (рис. 1). Если угловая скорость диска ω, а скорость его центра υ, то скорости точек, соприкасающихся с рейками, будут соответственно равны
(Мы приняли для определенности, что υ1 > υ2). Решая эти системы, находим:
а)
б)
3. Скорость любой точки М, лежащей на отрезке ОВ (см. рис. 2), находится по формуле υM = υ + ω·rM, где rM — расстояние от точки М до центра диска О. Для любой точки N, принадлежащей отрезку ОА, имеем: υN = υ – ω·rN, где rN — расстояние от точки N до центра. Обозначим через ρ расстояние от любой точки диаметра ВА до точки А соприкосновения диска с плоскостью. Тогда очевидно, что rM = ρ – R и rN = R – ρ = –(ρ – R). где R — радиус диска. Поэтому скорость любой точки на диаметре ВА находится по формуле: υρ = υ + ω·(ρ – R). Так как диск катится без проскальзывания, то 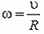
Доказанное утверждение позволяет нам сделать вывод, что сложное движение точек, находящихся на диаметре ВА, можно в каждый данный момент рассматривать как простое вращение вокруг неподвижной точки А с угловой скоростью ω, равной угловой скорости вращения вокруг центра диска. В самом деле, в каждый момент скорости этих точек направлены перпендикулярно диаметру ВА, а по величине равны произведению ω на расстояние до точки А.
Оказывается, что это утверждение справедливо для любой точки диска. Более того, оно является общим правилом. При любом движении твердого тела в каждый момент существует ось, вокруг которой тело просто вращается — мгновенная ось вращения.
4. На самолет действуют (см. рис. 3) сила тяжести Р = m·g и подъемная сила N, направленная перпендикулярно плоскости крыльев (так как самолет движется с постоянной скоростью, то сила тяги и сила лобового сопротивления воздуха уравновешивают друг друга). Равнодействующая сил Р и N должна быть направлена к центру окружности, по которой движется самолет, и создавать центростремительное ускорение 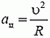
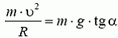
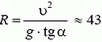
5. Равнодействующая силы тяжести Р = m·g и силы натяжения нити Т должна создавать центростремительное ускорение ац = ω 2 ·R, где R = l·sin α — радиус круга, по которому вращается груз. Из рисунка 4 получаем:
m·ω 2 ·R = m·g·tg α, откуда
Период обращения груза
Натяжение нити
6. На автомобиль действуют (рис. 5) сила тяжести Р = m·g, сила реакции со стороны цилиндра N и сила трения Fтp. Так как автомобиль движется по горизонтальному кругу, то силы Р и Fтp уравновешивают друг друга, а сила N создает центростремительное ускорение 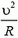
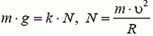
7. Груз будет двигаться по окружности радиуса l (рис. 6). Центростремительное ускорение груза 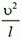
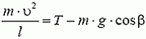
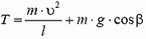
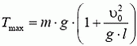
Используя это соотношение, для максимального значения натяжения нити получаем формулу: Tmax = m·g·(3 – 2 cos α). По условию задачи Tmах = 2m·g. Приравнивая эти выражения, находим cos α = 0,5 и, следовательно, α = 60°.
Определим теперь натяжение нити при 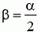
Подставляя значение υ1 в формулу для силы натяжения, находим:
💡 Видео
Движение тел по окружностиСкачать

Физика 9 класс (Урок№4 - Движение тела по окружности. Период и частота)Скачать

Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Физика 9 класс (Урок№1 - Движение тела, брошенного вертикально вверх)Скачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Движение тела, брошенного под углом к горизонтуСкачать

Урок 90. Движение по окружности (ч.2)Скачать

Урок 89. Движение по окружности (ч.1)Скачать

9 класс, 10 урок, Движение тела, брошенного вертикально вверхСкачать

Движение тела, брошенного вертикально вверхСкачать

Урок 34. Свободное падение. Ускорение свободного паденияСкачать

7.3. Движение тела, брошенного вертикально вверх и внизСкачать

Лекция 4.4 | Движение тела, брошенного вертикально вверх | Александр Чирцов | ЛекториумСкачать

Движение тела под действием силы тяжести. 1 часть. 9 класс.Скачать

Физика - движение тела, брошенного под углом к горизонтуСкачать