Материальная точка м движется по окружности в направлении (2 видео)

Кинематика поступательного движения

Автомобиль движется с постоянной по модулю скоростью по траектории, представленной на рисунке. В какой из указанных точек траектории центростремительное ускорение максимально?

Материальная точка м движется по окружности в направлении

#1 #2 #3 #Во всех точках одинаково

Точка М движется по спирали в направлении, указанном стрелкой. Нормальное ускорение по величине не изменяется. При этом величина скорости …

# уменьшается # увеличивается # не изменяется

Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина нормального ускорения …

# уменьшается # увеличивается # не изменяется

# увеличивается # уменьшается # не изменяется

Точка М движется по окружности с постоянным тангенциальным ускорением. Если проекция тангенциального ускорения на направление скорости положительна, то величина нормального ускорения…

# увеличивается # уменьшается # не изменяется

Точка М движется по окружности с постоянным тангенциальным ускорением. Если проекция тангенциального ускорения на направление скорости отрицательна, то величина нормального ускорения…

# уменьшается # увеличивается # не изменяется

Материальная точка M движется по окружности со скоростью . На рис. 1 показан график зависимости V_τ от времени ( – единичный вектор положительного направления, V_τ – проекция на это направление). На рис. 2 укажите направление ускорения т.М в момент времени t₂.

Если a_t и a_n – тангенциальная и нормальная составляющие ускорения, то для равномерного движения по окружности справедливы соотношения:

Если a_t и a_n – тангенциальная и нормальная составляющие ускорения, то соотношения: a_t = a = const, a_n = 0 справедливы для.

#прямолинейного равноускоренного движения #прямолинейного равномерного движения #равномерного криволинейного движения #равномерного движения по окружности

Если a_t и a_n – тангенциальная и нормальная составляющие ускорения, то соотношения: a_t = 0, a_n = const справедливы для.

#равномерного криволинейного движения #прямолинейного равноускоренного движения #прямолинейного равномерного движения #равномерного движения по окружности

Два тела брошены под одним и тем же углом к горизонту с начальными скоростями V₀и 2V₀. Если сопротивлением воздуха пренебречь, то соотношение дальностей полета S₂/S₁ равно .

Материальная точка М движется по окружности со скоростью . На рис. 1 показан график зависимости проекции скорости от времени ( – единичный вектор положительного направления, – проекция на это направление). При этом для нормального a_n и тангенциального a_t ускорения выполняются условия.

# – увеличивается, – постоянно # – постоянно, – увеличивается # – увеличивается, – увеличивается # – постоянно, – постоянно

Камень бросили под углом к горизонту соскоростью V₀. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет.

Модуль тангенциального ускорения a_t на участке А-В-С…

# увеличится # не изменяется # уменьшается

Автомобиль движется с постоянной по величине скоростью по траектории, представленной на рисунке. В какой из указанных точек траектории полное ускорение минимально?

#1 #2 #3 #Во всех точках одинаково

Тело брошено с поверхности Земли со скоростью 20 м/с под углом 45° к горизонту. Определите радиус кривизны его траектории в верхней точке. Сопротивлением воздуха пренебречь. (g = 10 м/с 2 ).

#10 м #20 м #30 м #80 м

Графики зависимости величины тангенциального ускорения от времени для равномерного движения тела по окружности изображен на рисунке.

# # # #

Точка М движется по спирали с постоянным по величине нормальным ускорением в направлении, указанном стрелкой. При этом проекция тангенциального ускорения на направление скорости .

#равна нулю #меньше нуля #больше нуля

# > 0; = 0 # = 0; 0; > 0 # > 0; a_B # a_A = a_B = 0 # a_A = a_B ≠ 0.

Тело брошено с поверхности Земли со скоростью 20 м/с под углом 60° к горизонту. Определите радиус кривизны его траектории в верхней точке. Сопротивлением воздуха пренебречь. (g = 10 м/с 2 ).

#10 м #20 м #30 м #80 м

Материальная точка движется по окружности. На чертеже изображена зависимость ее скорости от времени. Точка имеет наибольшее тангенциальное ускорение в момент времени .

Тело брошено под углом к горизонту и движется в поле силы тяжести Земли. На рисунке изображен восходящий участок траектории данного тела.

Правильно изображает полное ускорение вектор .

Тело брошено с поверхности Земли со скоростью 20 м/с под углом 30° к горизонту. Определите радиус кривизны его траектории в верхней точке. Сопротивлением воздуха пренебречь. (g = 10 м/с 2 ).

#10 м #20 м #30 м #80 м

Тангенциальное ускорение точки меняется согласно графику.

Такому движению соответствует зависимость скорости от времени .

# # # # .

Содержание

Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Период, частота и количество оборотов
Линейная и угловая скорости
Линейная скорость
Угловая скорость
Центростремительное ускорение
Криволинейное движение материальной точки Движение по окружности
📸 Видео

Видео:Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Движение по окружности с постоянной по модулю скоростью

теория по физике 🧲 кинематика

Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:

Траектория движения тела есть окружность.
Вектор скорости всегда направлен по касательной к окружности.
Направление скорости постоянно меняется под действием центростремительного ускорения.
Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Видео:Физика - движение по окружностиСкачать

Линейная и угловая скорости

Линейная скорость

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂.
У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Видео:Материальная точка движется по окружности радиусом R с постоянной по модулю скоростьюСкачать

Центростремительное ускорение

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_ц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Алгоритм решения

Записать исходные данные.
Записать формулу для определения искомой величины.
Подставить известные данные в формулу и произвести вычисления.

Решение

Записываем исходные данные:

Радиус окружности, по которой движется автомобиль: R = 100 м.
Скорость автомобиля во время движения по окружности: v = 20 м/с.

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?

а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза

Алгоритм решения

Записать исходные данные.
Определить, что нужно найти.
Записать формулу зависимости центростремительного ускорения от частоты.
Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
Приравнять правые части формул и найти искомую величину.

Решение

Запишем исходные данные:

Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Видео:Центростремительное ускорение. 9 класс.Скачать

Криволинейное движение материальной точки Движение по окружности

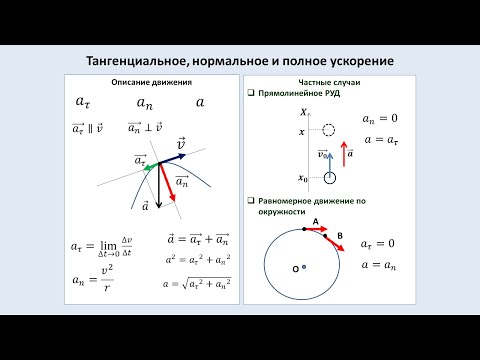
Если траектория — кривая линия, то движение называется криволинейным. В каждой точке траектории скорость v направлена по касательной к ней. Скорость в общем случае — функция времени и изменяется как по величине, так и по направлению (рис. 8).

В общем случае ускорение а направлено под углом к скорости и также изменяется как по величине, так и по направлению. По правилам действия над векторами представим ускорение в виде двух составляющих. Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением а_т. Эта составляющая характеризует изменение скорости dv по величине и определяется отношением малого изменения скорости dv по модулю к малому промежутку времени, за которое произошло это изменение:

Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно скорости, называется нормальным ускорением а_п. Эта составляющая характеризует изменение скорости по направлению

где R — радиус кривизны траектории в данной точке. Модуль полного ускорения определяется по формуле

Пусть материальная точка движется по окружности радиусом R. Одной из характеристик движения является угол поворота точки от некоторого начального положения. Угол поворота Дф = ф — ф₀. Если принять, что в начальный момент времени t₀ материальная точка находилась в точке А, то угол ф₀ можно считать равным нулю (рис. 9). За малый промежуток времени d? точка повернется на малый угол йф. Физическая величина, определяемая отношением малого угла поворота материальной точки к малому промежутку времени, за которое произошло это изменение, называется угловой скоростью со:

Из геометрических соображений длина малого участка дуги

где cb—модуль элементарного перемещения точки.

Используя выражение (3) п. 1.3, получаем связь между линейной и угловой скоростью движения по окружности:

Если угловая скорость со = const (и линейная тоже), то движение называется равномерным движением по окружности. В этом случае в любой момент времени угловая скорость

где At — промежуток времени, Дф — угол поворота материальной точки за этот промежуток времени. Таким образом, угловая скорость определяется углом поворота за единицу времени.

Единица угловой скорости в СИ — радиан в секунду (рад/с). 1 рад/с равен угловой скорости равномерно вращающегося тела, все точки которого за время 1 с поворачиваются относительно оси на угол 1 рад.

Угловой скорости приписывается направление вдоль оси вращения, определяемое правилом буравчика. Если вращать буравчик в сторону линейной скорости, то его поступательное движение задает направление угловой скорости. На рис. 9 вектор угловой скорости направлен на нас, что изображается точкой в центре кружка.

Для нормальной составляющей ускорения при движении по окружности, учитывая выражение (3), получим

Тангенциальная составляющая ускорения при равномерном движении по окружности

Равномерное движение по окружности можно характеризовать периодом вращения Т — временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2к.

Так как промежуток времени At = Т соответствует Дер = 2 к, 2к

то со=—, откуда со

Число полных оборотов, совершаемых телом при равномерном его движении по окружности в единицу времени, называется частотой вращения:

Единица частоты в СИ — секунда в минус первой степени (с -1 ). 1 с -1 равна частоте, при которой тело, равномерно вращаясь, за время 1 с совершает 1 оборот.

Если за промежуток времени At = t-t₀ угловая скорость изменилась на величину Дсо=о)-со₀, то материальная точка будет обладать угловым ускорением

характеризующим быстроту изменения угловой скорости. Таким образом, угловое ускорение определяет изменение угловой скорости за единицу времени. В пособии рассматривается движение с постоянным угловым ускорением, поэтому среднее и мгновенное угловые ускорения совпадают.

Единица углового ускорения в СИ — радиан на секунду в квадрате (1 рад/с 2 ). 1 рад/с 2 равен угловому ускорению равноускоренно вращающегося тела, при котором оно за время 1 с изменяет скорость на 1 рад/с.

Если угловая скорость возрастает — >0 , то вектор уг-

лового ускорения ё сонаправлен вектору & (рис. 10, а). Если , (Дй

угловая скорость убывает — At

рения ё противонаправлен вектору й) (рис. 10, б).

Нормальная составляющая ускорения согласно формуле (4),