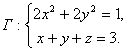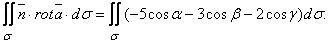Вычислить циркуляцию векторного поля по контуру окружности (7 видео)

Вычислить циркуляцию векторного поля по контуру окружности

&nbsp &nbsp &nbsp &nbsp Вариант 1 &nbsp &nbsp Вариант 2 &nbsp &nbsp Вариант 3 &nbsp &nbsp Вариант 4 &nbsp &nbsp Вариант 5 &nbsp &nbsp Вариант 6

&nbsp &nbsp &nbsp &nbsp Вариант 7 &nbsp &nbsp Вариант 8 &nbsp &nbsp Вариант 9 &nbsp &nbsp Вариант 10 &nbsp &nbsp Вариант 11 &nbsp &nbsp Вариант 12

&nbsp &nbsp Вариант 13 &nbsp &nbsp Вариант 14 &nbsp &nbsp Вариант 15 &nbsp &nbsp Вариант 16 &nbsp &nbsp Вариант 17 &nbsp &nbsp Вариант 18

&nbsp &nbsp Вариант 19 &nbsp &nbsp Вариант 20 &nbsp &nbsp Вариант 21 &nbsp &nbsp Вариант 22 &nbsp &nbsp Вариант 23 &nbsp &nbsp Вариант 24

&nbsp &nbsp Вариант 25 &nbsp &nbsp Вариант 26 &nbsp &nbsp Вариант 27 &nbsp &nbsp Вариант 28 &nbsp &nbsp Вариант 29 &nbsp &nbsp Вариант 30

&nbsp &nbsp &nbsp &nbsp 12.14 Найти модуль циркуляции векторного поля 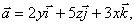&nbsp &nbsp
вдоль контура
&nbsp &nbsp

Содержание

Решение
Циркуляция векторного поля. Ротор вектора. Теорема Стокса
Пример 3:
Правила вычисления ротора
Примеры решений задач по теории поля
Примеры: базовые понятия теории поля
Поток поля через поверхность
Циркуляция векторного поля
Работа векторного поля
Типовой расчет по теории поля
Помощь с решением заданий
💥 Видео

Решение

&nbsp &nbsp &nbsp &nbsp Согласно формуле Стокса:

.
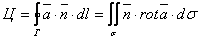
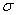
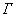
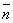
&nbsp &nbsp &nbsp &nbsp Здесь &nbsp &nbsp &nbsp &nbsp — участок поверхности, ограниченный контуром &nbsp &nbsp &nbsp &nbsp , &nbsp &nbsp &nbsp &nbsp — единичный вектор нормали к данной поверхности.

&nbsp &nbsp &nbsp &nbsp Найдём ротор векторного поля

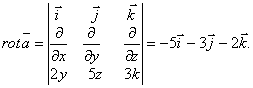
&nbsp &nbsp &nbsp &nbsp Тогда интеграл запишется

&nbsp &nbsp &nbsp &nbsp Здесь &nbsp &nbsp &nbsp &nbsp — направляющие косинусы нормали к поверхности или координаты единичного вектора нормали.
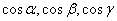
&nbsp &nbsp &nbsp &nbsp Из общего уравнения плоскости запишем координаты нормального вектора 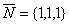&nbsp &nbsp &nbsp .
&nbsp &nbsp &nbsp &nbsp Находим длину нормального вектора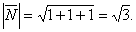
.
&nbsp &nbsp &nbsp &nbsp Тогда направляющие косинусы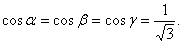
.

&nbsp &nbsp &nbsp &nbsp Элемент поверхности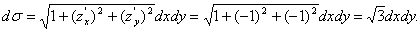
.

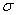
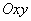
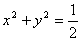
&nbsp &nbsp &nbsp &nbsp Проекцией поверхности &nbsp &nbsp &nbsp &nbsp на плоскость &nbsp &nbsp &nbsp &nbsp является круг

&nbsp &nbsp &nbsp &nbsp Этот круг имеет центр в начале координат и радиус 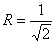&nbsp &nbsp &nbsp &nbsp.

&nbsp &nbsp &nbsp &nbsp Площадь данного круга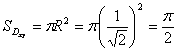
.
&nbsp &nbsp &nbsp &nbsp Переходя от поверхностного интеграла к двойному, получим

&nbsp &nbsp &nbsp &nbsp Тогда модуль циркуляции 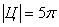&nbsp &nbsp &nbsp .
&nbsp &nbsp &nbsp &nbsp Ответ: Модуль циркуляции равен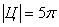&nbsp &nbsp &nbsp .

Видео:Формула Стокса.ЦиркуляцияСкачать

Циркуляция векторного поля. Ротор вектора. Теорема Стокса

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Пусть в некоторой области G задано непрерывное векторное поле а ) к и замкнутый ориентированный контур L. Определение 1. Циркуляцией вектора а по замкнутому контуру L называется криволинейный интеграл 2-го рода от оектора а по контуру L Здесь dr — вектор, длина которого равна дифференциалу дуги L, а направление совпадаете направлением касательной к L, оп- Рис. 31 ределяемымориентацией контура (рис. 31); символ f означает, что интеграл берется по зам1«угому контуру L. ь

Пример 1. вычислить циркуляцию векторного поля вдоль эллипса L: По определению циркуляции имеем Параметрические уравнения данного эллипса имеют вид: , и, значит, . Подставляя эти выражения в формулу (2), найдем Циркуляция векторного поля. Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля Правила вычисления ротора 8.1.

Ротор (вихрь) векторного поля Рассмотрим поле вектора Р, Q, R которого непрерывны и имеют непрерывные частные производные первого порядка по всем своим аргументам. Огределенив 2. Ротором вектора »(М) называется вектор, обозначаемый символом rot а и определяемый равенством или, в символической, удобной для запоминания форме, Этот определитель раскрывают по элементам первой строки, при этом операции умножения элементов второй строки на элементы третьей строки понимаются как операции дифференцирования, например,

Определение 3. Если в некоторой области G имеем rot а = 0, то поле вектора а в области G называете я безвихревым. Пример 2. Найти ротор вектора 4 Согласно формуле (3) имеем Так как rot а — вектор, то мы можем рассматривать векторное поле — поле ротора вектора а. Предполагая, что координаты вектора а имеют непрерывные частные производные второго порядка, вычислим дивергенцию вектора rot а. Получим Таким образом, поле вектора rot а соленоида л ьно.

Теорема 7 (Стокса). Циркуляция вектора а вдоль ориентированного замкнутого контура L равна потоку ротора этого вектора через любую поверхность Е, натянутую на контур L, При этом предполагается, что координаты вектора а имеют непрерывные частные производные в некоторой области G пространства, содержащей поверхность Е, и что ориентация орта нормали п° к поверхности ЕС G согласована с ориентацией контура L так, что из конца нормши обход контура в заданном направлении виден совершающимся против часовой стрелки.

Учитывая, что , и пользуясь определением ротора (3), перепишем формулу (4) в следующем виде: Рассмотрим сначала случай, когда гладкая поверхность Е и ее контур L однозначно проектируются на область D плоскости хОу и ее границу — контур А соответственно (рис. 32). Ориентация контура L порождает определенную ориентацию контура А. Для определенности будем считать, что контур L ориентирован так, что поверхность Е остается слева, так что веетор нормали п к поверхности Е составдя етсосью Oz острый угол 7 (cos 7 >0).

Возможно вам будут полезны данные страницы:

Пусть — уравнение поверхности Е и функция ф(х>у) непрерывна и имеет непрерывные частные производные gf и ^ в замкнутой области D.

Рассмотрим интеграл Линия L лежит на поверхности Е. Поэтому, пользуясь уравнением этой поверхности , мы можем заменить г под знаком интеграла на ^(ж, у). Координаты перемсннойточки кривой А равны координатам соответствующей точки на кривой L, а потому интегрирование по L можно заменить интегрированием по А, Применим к интегралу, стоящему справа, формулу Грина.

Имеем Перейдем теперь от интеграла по области D к интегралу по поверхности Е. Так как dS = cos 7 • da, то из формулы (8) получим, что Вектор нормали п° к поверхности Е определяется выражением к. Отсюда видно, что . Поэтому равенсгво (9) можно переписать так: Считая Е гладкой поверхностью, однозначно проектирующейся на все три координатные плоскости, аналогично убеждаемся в справедливости формул Циркуляция векторного поля.

Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля Правила вычисления ротора Складывая равенства почленно, получим формулу Стокса (5), или, короче, Замечание 1. Мы показали, что поле вектора rote — соленоидальное, и потому поток вектора rota не зависит от вида поверхности Е, натянутой на контур L. Замечание 2. Формула (4) выведена в предположении, что поверхность £ однозначно проектируется на все три координатные плоскости. Бели это условие не выполнено, то разбиваем £ на частя так, чтобы каждая часть указанному условию удовлетворяла, а затем пользуемся аддитивностью интегралов.

Пример 3:

Вычислить циркуляцию вектора по линии 1) пользуясь определением; 2) по теореме Стокса. 4 1) Зададим линию L параметрически: Тогда 2) Найдем rota: Натянем на контур L кусок плосхости Тогда . Инвариантное определение ротора поля Из теоремы Стокса можно получить инвариантное определение ротора поля, не связанное с выбором системы координат. Теорема 8.

Проекция ротора а на любое направление не зависит от выбора системы координат и равна поверхностной плотности циркуляции вектора а по контуру площадки, перпендикулярной этому направлению, Здесь (Е) — плоская площадка, перпендикулярная вектору л; 5 — площадь этой площадки; L — контур площадки, ориентированный так, чтобы обход контура был виден из конца вектора п против хода часовой стрелки; (Е) М означает, что площадка (Е) стягивается к точке М, в которой рассматривается вектор rot а, причем вектор нормали п к этой площадке остается все время одним и тем же (рис. 33). 4

Применим сначала к циркуляции (a,dr) вектора а теорему Стокса, а затем к полученному двойному интегралу — теорему о среднем значении: откуда (скалярное произведение берется в некоторой средней точке Мф площадки (Е)). Пристягивании площадки (Е) кточке М средняяточка Л/ср тоже стремится кточ-ке М и, в силу предполагаемой непрерывности частных производных от координат вектора а (а значит, и непрерывности rot а), мы получаем Поскольку проекция вектора rot а на произвольное направление не зависитотвы-бора системы координат,то и сам вектор rota инвариантен относительно этого выбора.

Отсюда получаем следующее инвариантное определение ротора поля: ротор поля есть вектор, длина которого равна наибольшей поверхностной плотности циркуляции в данной точке, направленный перпендикулярно той площадке, на которой эта наибольшая плотность циркуляции достигается; при этом ориентация вектора rota согласуется с ориентацией контура, при которой циркуляция положительна, по правилу правого винта. 8.3.

Физический смысл ротора поля Пустьтвердое

тело вращается вокруг неподвижной оси I с угловой скоростью и. Не нарушая общности, можно считать, что ось I совпадает с осью Oz (рис. 34). Пусть М(г) — изучаемая точка тела, где Вектор угловой скорости в нашем случае равен из = wk, вычислим вектор v линейной скорости точки М, Отсюда Циркуляция векторного поля. Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля.

Правила вычисления ротора

Итак, вихрь поля скоростей вращающегося твердого тела одинаков во всех точках поля, параллелен оси вращения и равен удвоенной угловой скорости вращения. 8.4. Правила вычисления ротора 1. Ротор постоянного вектора с равен нулевому вектору, 2. Ротор обладает свойством линейности постоянные числа. 3. Ротор произведения скалярной функции и<М) на векторную а(М) вычисляется по формуле

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Непосредственное вычисление циркуляцииСкачать

Примеры решений задач по теории поля

В этом разделе вы найдете готовые задания разного типа по векторному анализу (теории поля):

Видео:Методы вычисления циркуляции векторного поляСкачать

Примеры: базовые понятия теории поля

Задача 1. Проверить, что поле $f=(3x+y^2)i+2xy j$ потенциально и восстановить потенциал.

Задача 2. Найти дивергенцию и ротор векторного поля $overline=(3x-y) overline+(6z+5x) overline$

Задача 4. Вычислить потенциальную функцию векторного поля

Видео:Поток векторного поля через замкнутую поверхностьСкачать

Поток поля через поверхность

Видео:Циркуляция векторного поля №1Скачать

Циркуляция векторного поля

с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).

Задача 12. Найти циркуляцию вектора $F$ вдоль ориентированного контура $L$. $$ overline = (3x-1) overline+ (y-x+z)overline+4z overline, $$ $L$ — контур треугольника $ABCA$, где $A,B,C$ точки пересечения плоскости $2x-y-2z+2=0$ соответственно с осями координат $Ox, Oy, Oz$.

Видео:Циркуляция векторного поля. Вычисление при при помощи криволинейного интеграла.Скачать

Работа векторного поля

Задача 13. Найдите работу векторного поля $A=(2xy-y; x^2+x)$ по перемещению материальной точки вдоль окружности $x^2+y^2=4$ из $M (2; 0)$ в $К(-2; 0)$.

Задача 14. Вычислить работу векторного поля силы $overline = xz overline -overline+y overline$ при движении материальной точки по пути $L: x^2+y^2+z^2=4$, $z=1 (y ge 0)$ от точки $M(sqrt(3);0;1)$ до точки $N(-sqrt(3);0;1)$.

Видео:Формула ГринаСкачать

Типовой расчет по теории поля

Задание 15.
А) Найти поток векторного поля $F$ через внешнюю поверхность пирамиды, отсекаемой плоскостью $(p)$ двумя способами: непосредственно и по формуле Гаусса-Остроградского.
Б) Найти циркуляцию вектора $F$ по контуру треугольника двумя способами: по определению и по формуле Стокса.

$$ overline = z overline+ (x+y)overline+y overline, quad (p): 2x+y+2z=2. $$

Видео:Циркуляция векторного поляСкачать

Помощь с решением заданий

Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей , оформление производится в Word, срок от 1 дня.