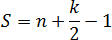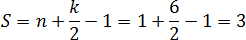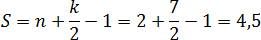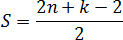Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок. Это даже не формула, а настоящая теорема. На первый взгляд, она может показаться сложной. Но достаточно решить пару задач — и вы поймете, насколько это крутая фишка. Так что вперед!
Для начала введем новое определение:
— это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.
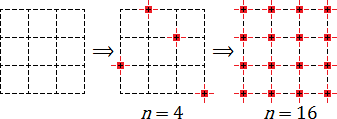
На первой картинке узлы вообще не обозначены. На второй обозначены 4 узла. Наконец, на третьей картинке обозначены все 16 узлов.
Какое отношение это имеет к задаче B5? Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки. Как следствие, для них работает следующая теорема:
Теорема. Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки. Тогда площадь многоугольника равна:
где n — число узлов внутри данного многоугольника, число узлов, которые лежат на его границе (граничных узлов).
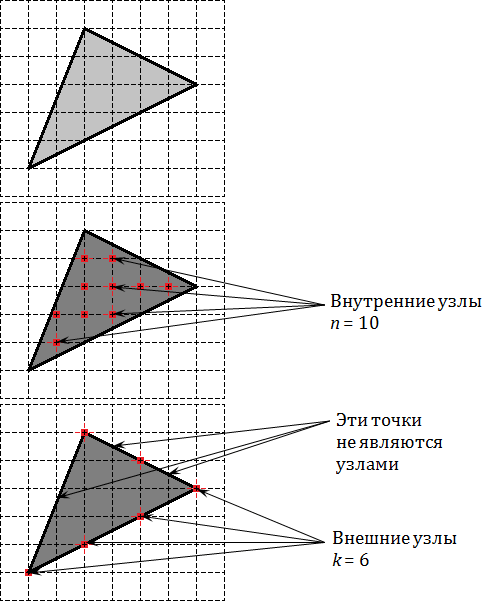
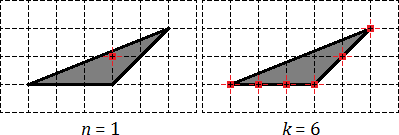
В качестве примера рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные узлы.
На первой картинке дан обычный треугольник. На второй отмечены его внутренние узлы, число которых равно На третей картинке отмечены узлы лежащие на границе, их всего
Возможно, многим читателям непонятно, как считать числа Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску.
С граничными узлами чуть сложнее. Граница многоугольника — замкнутая ломаная, которая пересекает координатную сетку во многих точках. Проще всего отметить какую-нибудь «стартовую» точку, а затем обойти остальные.
Граничными узлами будут только те точки на ломаной, в которых одновременно пересекаются
- Собственно, ломаная;
- Горизонтальная линия координатной сетки;
- Вертикальная линия.
Посмотрим, как все это работает в настоящих задачах.
Задача. Найдите площадь треугольника, если размер клетки равен 1 x 1 см:
Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе:
Получается, что внутренний узел всего один: Граничных узлов — целых шесть: три совпадают с вершинами треугольника, а еще три лежат на сторонах.
Теперь считаем площадь по формуле:
Вот и все! Задача решена.
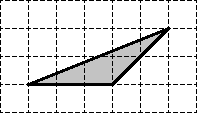
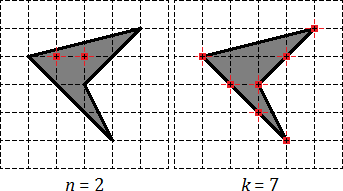
Задача. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см. Ответ дайте в квадратных сантиметрах.
Снова отмечаем внутренние и граничные узлы. Внутренних узлов всего Граничных узлов: из которых 4 являются вершинами четырехугольника, а еще 3 лежат на сторонах.
Остается подставить числа в формулу площади:
Обратите внимание на последний пример. Эту задачу реально предлагали на диагностической работе в 2012 году. Если работать по стандартной схеме, придется делать много дополнительных построений. А методом узлов все решается практически устно.
- Важное замечание по площадям
- Теория графов. Основные понятия и виды графов
- Теория графов
- Основные понятия теории графов
- Путь и цепь в графе
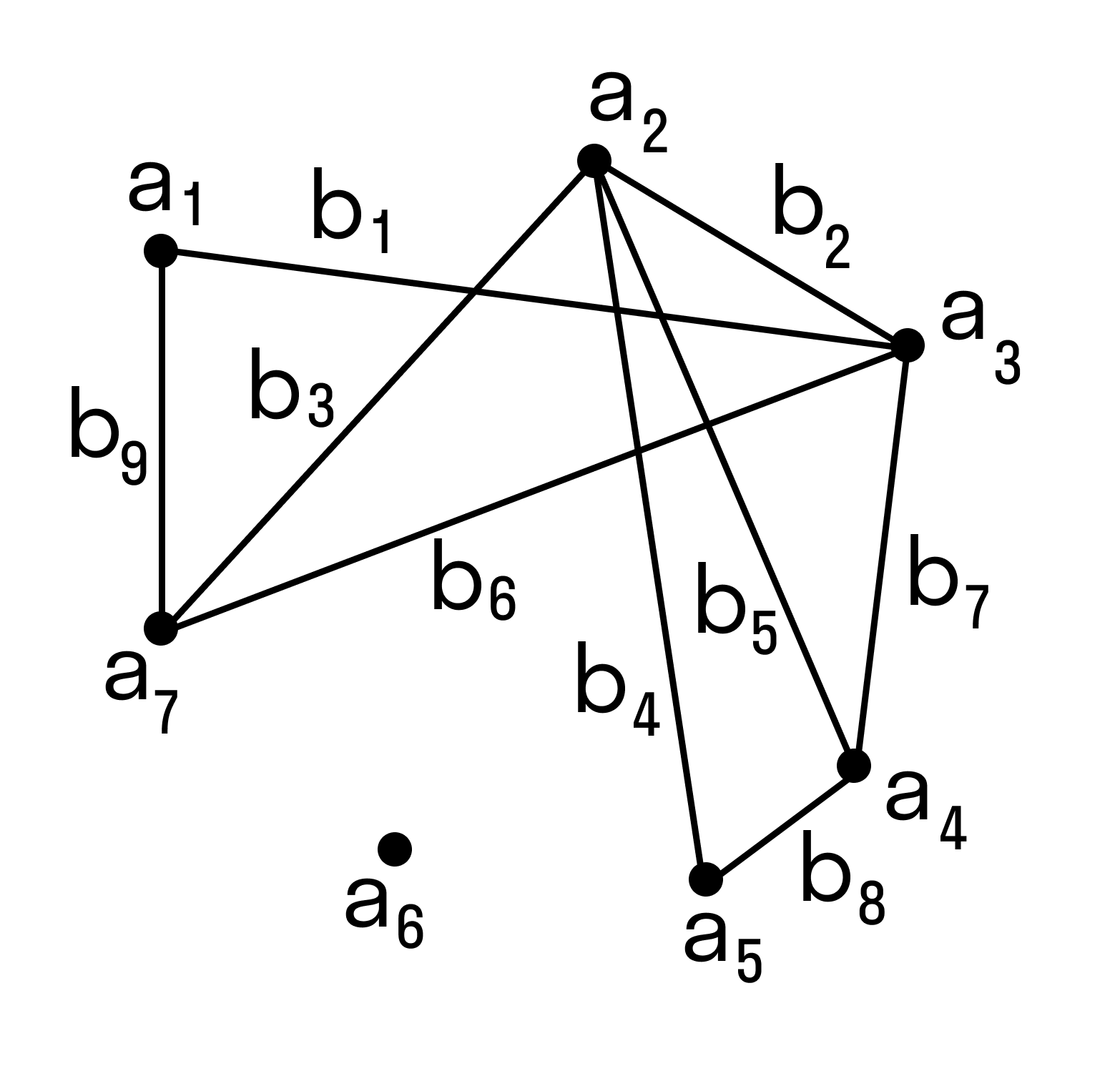
- Визуализация графовых моделей
- Виды графов
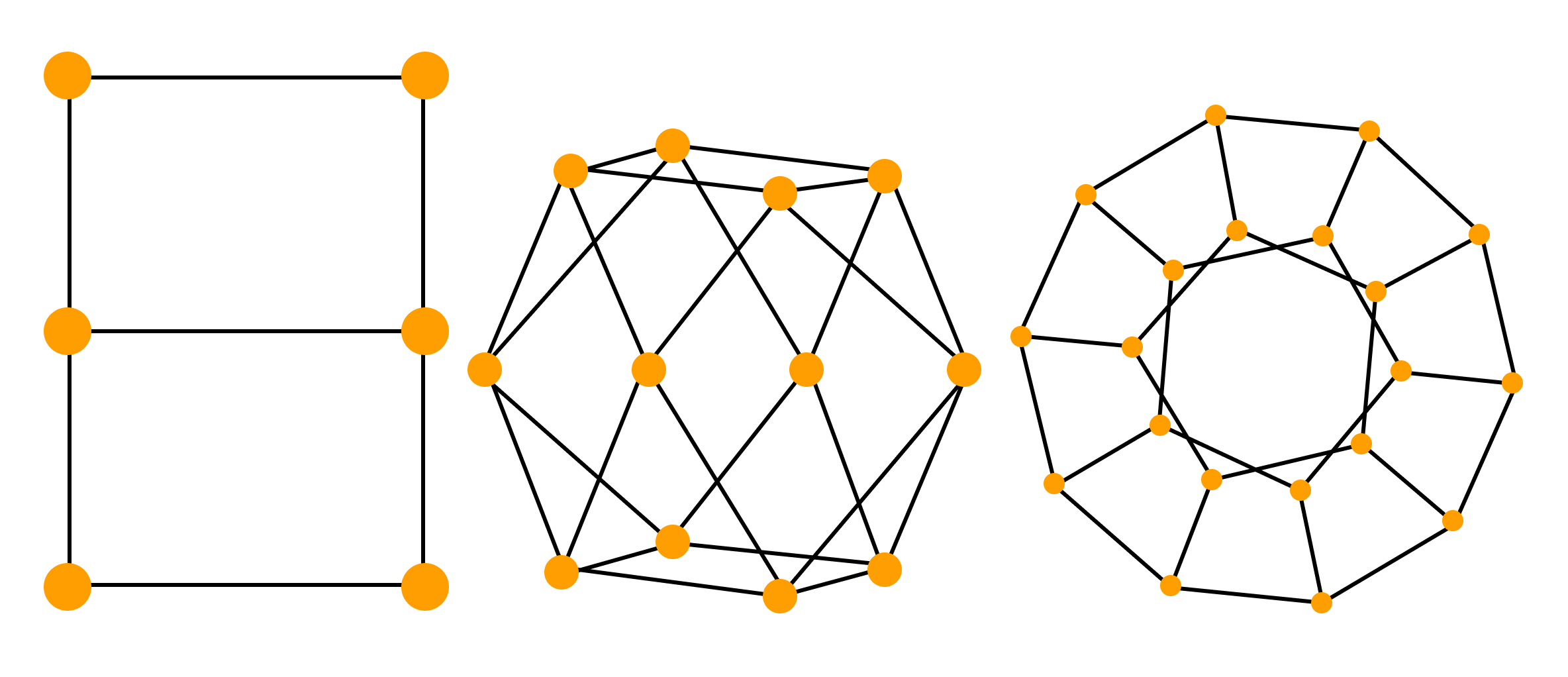
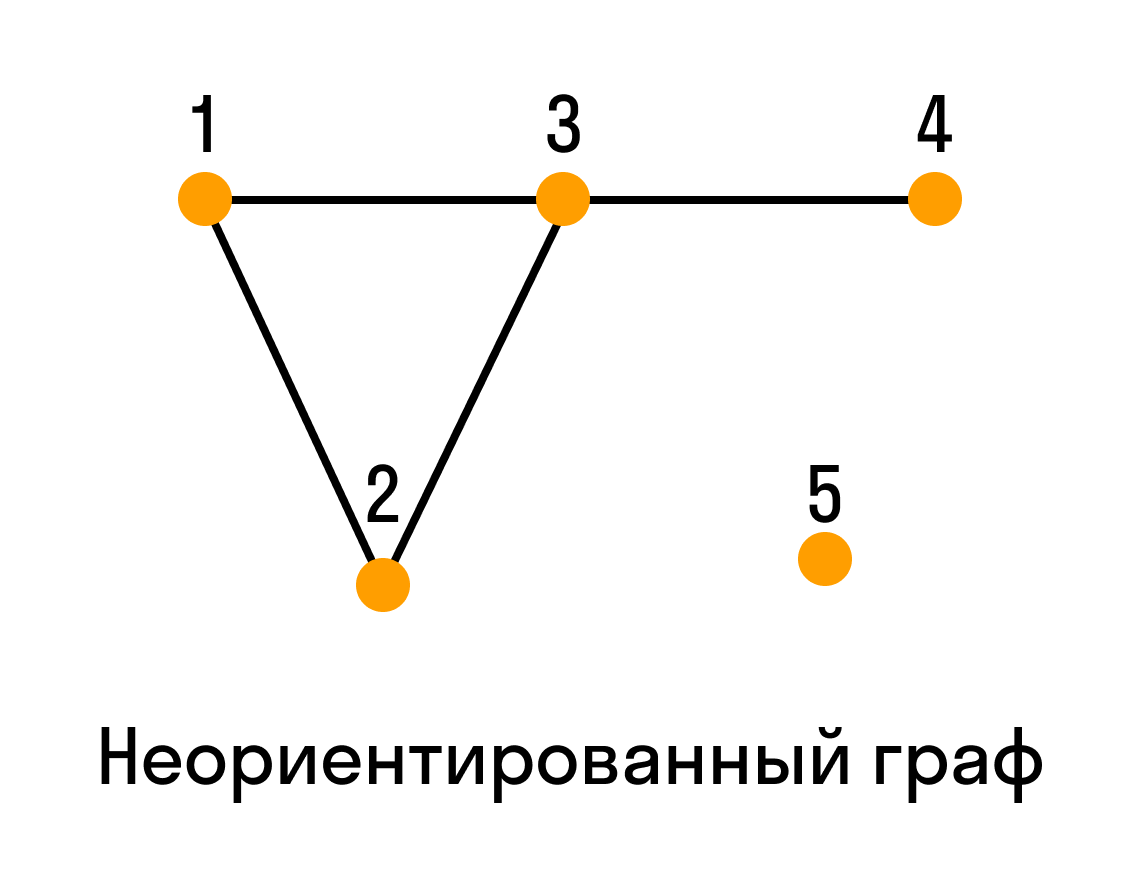
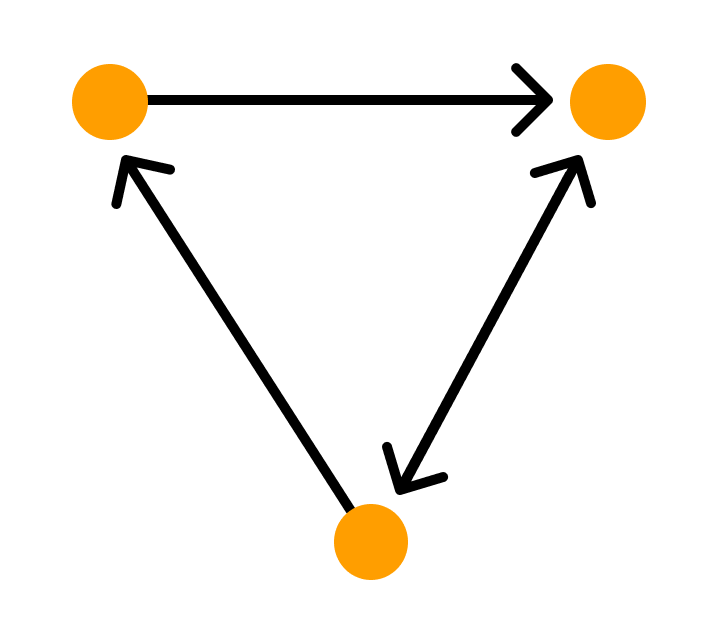
- Ориентированные и неориентированные графы
- Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы
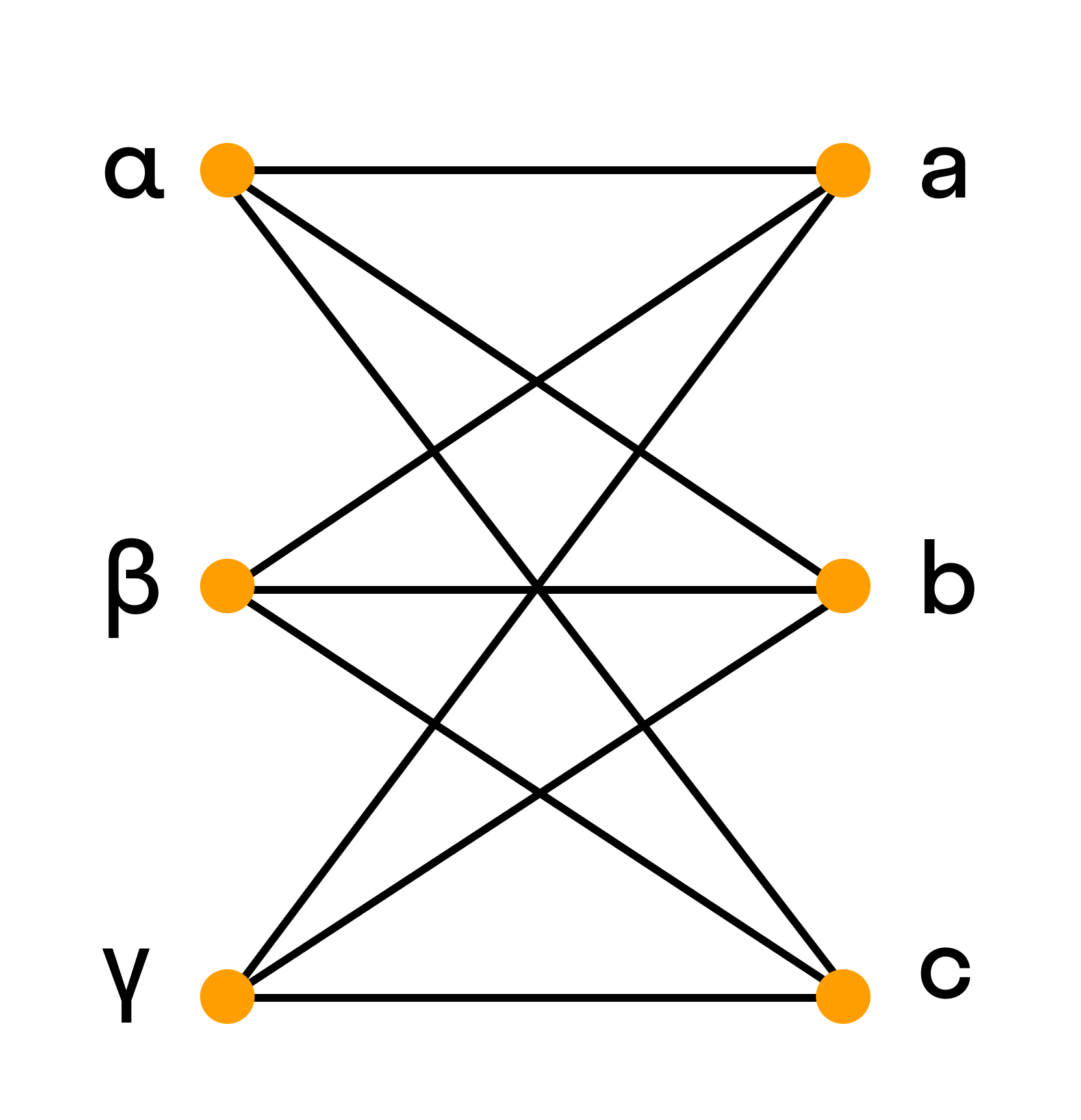
- Двудольный граф
- Эйлеров граф
- Регулярный граф
- Гамильтонов граф
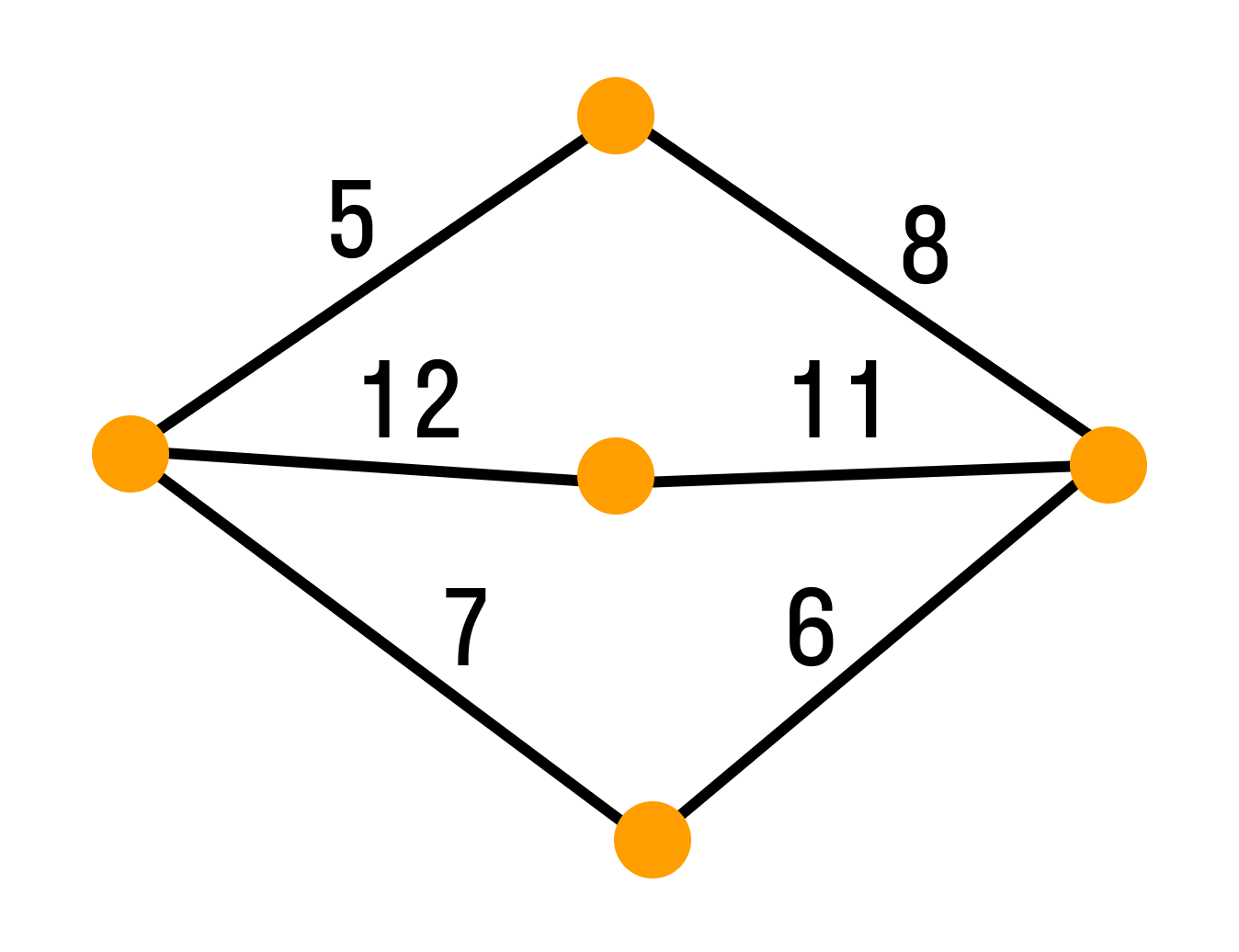
- Взвешенный граф
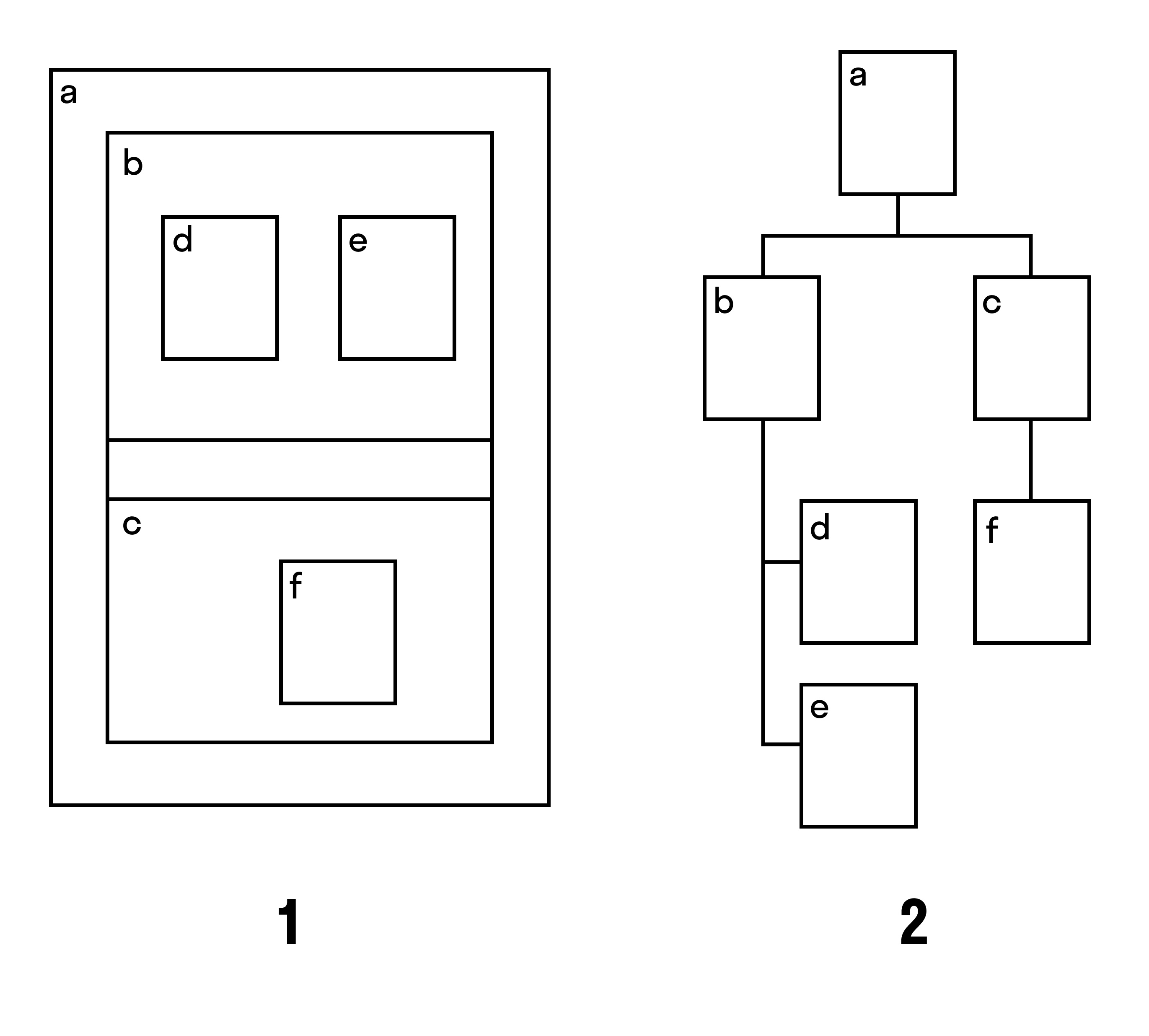
- Графы-деревья
- Определение дерева
- Теоремы дерева и их доказательства
- Теория графов и современные прикладные задачи
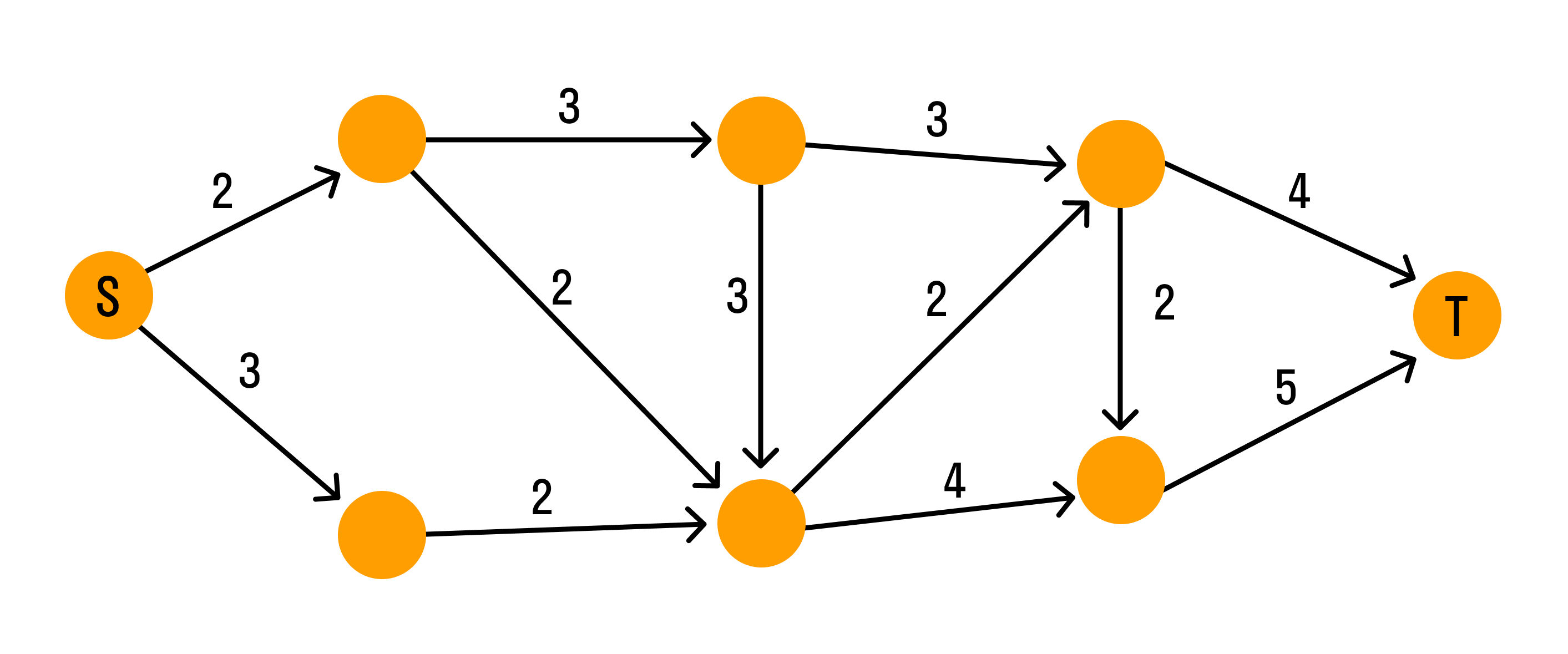
- Графы и задача о потоках
- Графы и сетевое планирование
- «Задачи на клетчатой бумаге»
- Главная > Реферат
- 📹 Видео
Видео:Хитрый и быстрый узел для вязки сети из лески.Скачать
Важное замечание по площадям
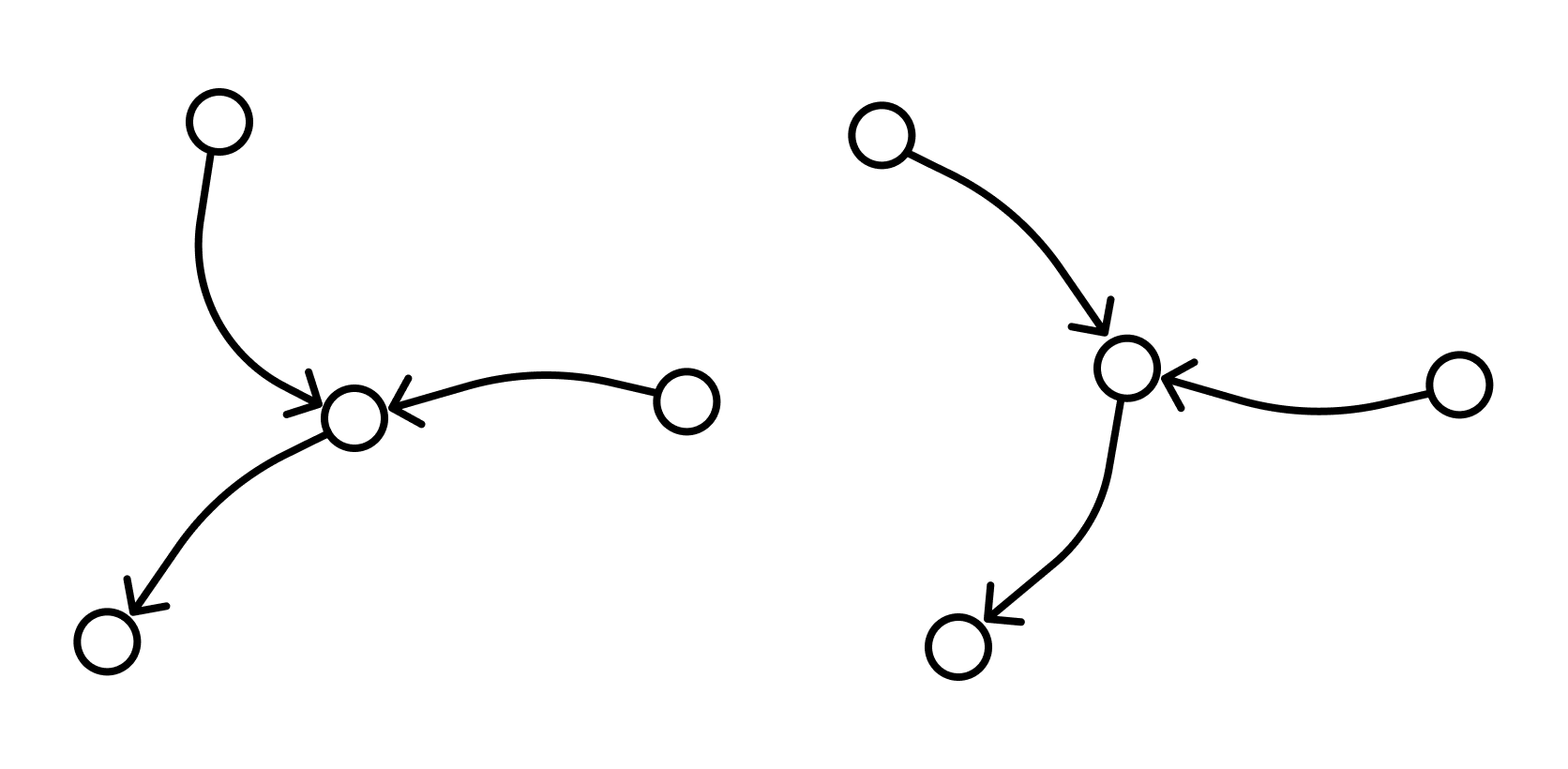
Но формула — это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю. Получим:
Числа n и k — это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:
Площадь всегда выражается целым числом или дробью. Причем в конце дроби всегда стоит «пять десятых»: 10,5; 17,5 и т.д.
Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!
Видео:ТОП 10 УЗЛОВ для ПОВСЕДНЕВНОЙ ЖИЗНИСкачать
Теория графов. Основные понятия и виды графов
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Как вяжется рыболовный узел? Изготовление рыболовной сетиСкачать
Теория графов
В переводе с греческого граф — «пишу», «описываю». В современном мире граф описывает отношения. И наоборот: любое отношение можно описать в виде графа.
Теория графов — обширный раздел дискретной математики, в котором системно изучают свойства графов.
Теория графов широко применяется в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических цепей, коммуникации, психологии, социологии, лингвистике и в других областях.
Для чего строят графы: чтобы отобразить отношения на множествах. По сути, графы помогают визуально представить всяческие сложные взаимодействия: аэропорты и рейсы между ними, разные отделы в компании, молекулы в веществе.
Давайте на примере.
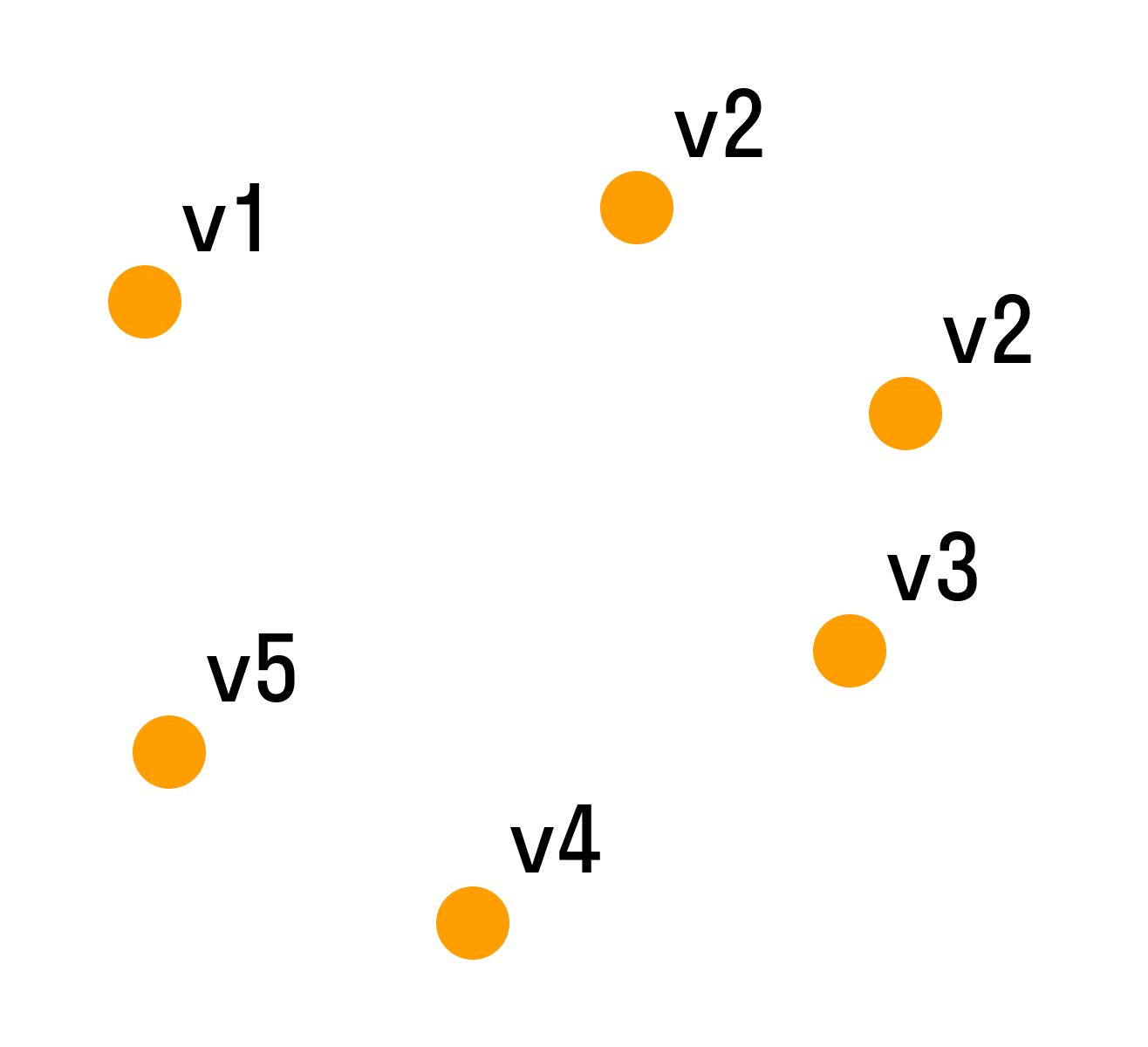
Пусть множество A = — это множество людей, и каждый элемент отображен в виде точки. Множество B = — множество связок (прямых, дуг или отрезков).
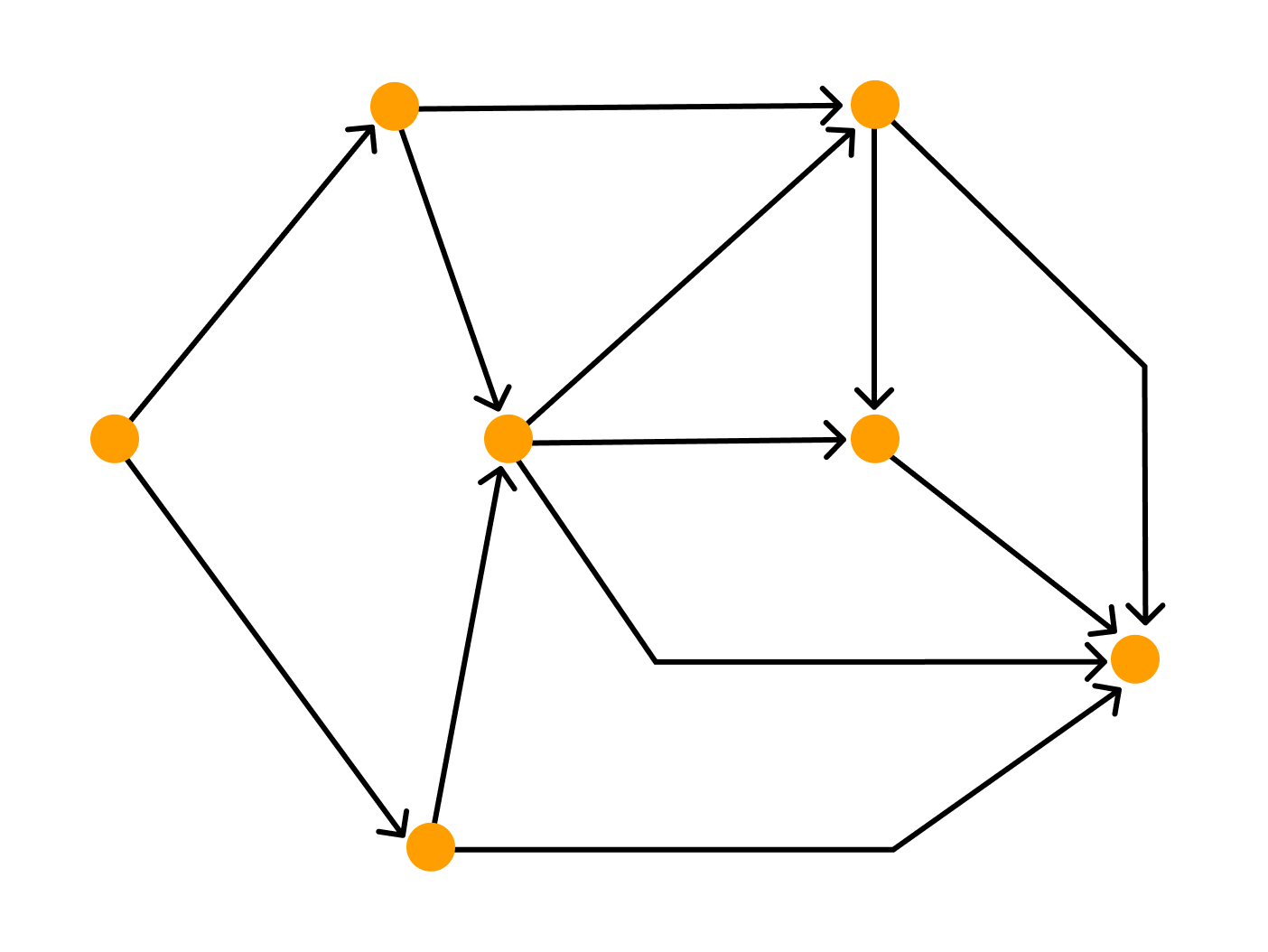
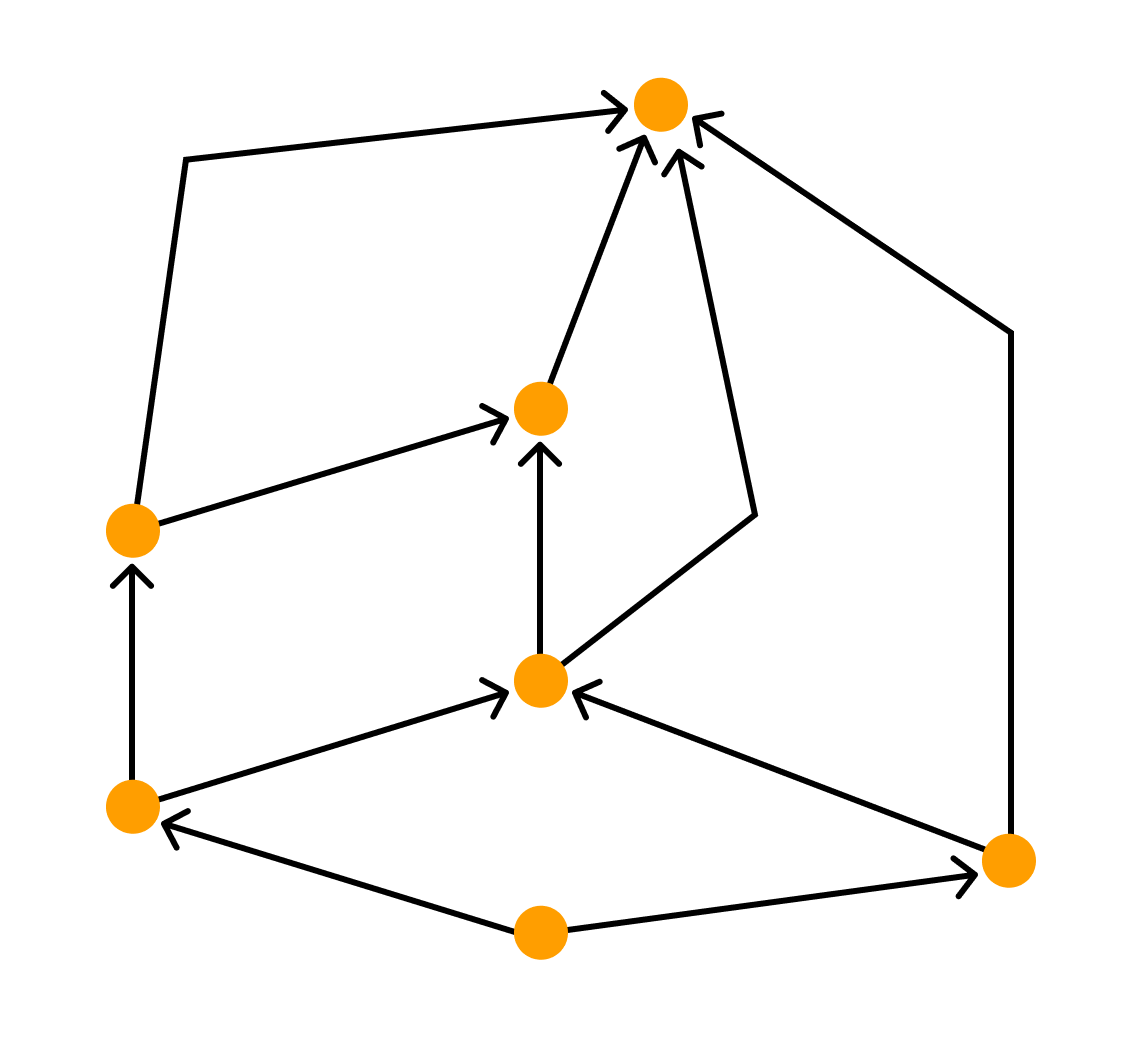
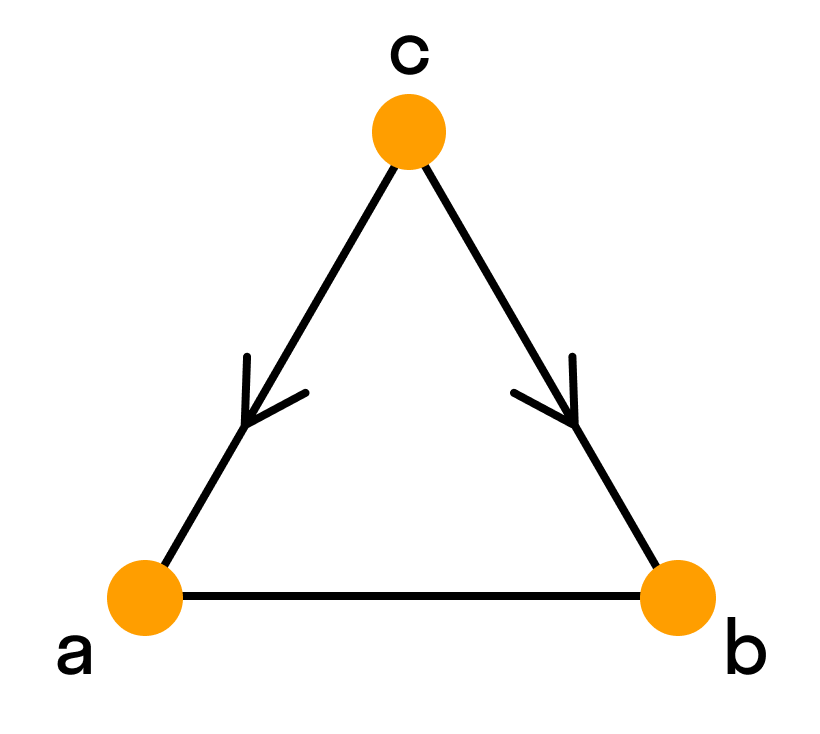
На множестве A зададим отношение знакомства между людьми из этого множества. Строим граф из точек и связок. Связки будут связывать пары людей, знакомых между собой.
Число знакомых у одних людей может отличаться от числа знакомых у других людей, некоторые могут вовсе не быть знакомы (такие элементы будут точками, не соединёнными ни с какой другой). Так получился граф:
В данном случае точки — это вершины графа, а связки — рёбра графа.
Теория графов не учитывает конкретную природу множеств A и B. Существует большое количество разных задач, при решении которых можно временно забыть о содержании множеств и их элементов. Эта специфика не отражается на ходе решения задачи.
Например, вопрос в задаче стоит так: можно ли из точки A добраться до точки E, если двигаться только по соединяющим точки линиям. Когда задача решена, мы получаем решение, верное для любого содержания, которое можно смоделировать в виде графа.
Не удивительно, что теория графов — один из самых востребованных инструментов при создании искусственного интеллекта: ведь искусственный интеллект может обсудить с человеком вопросы отношений, географии или музыки, решения различных задач.
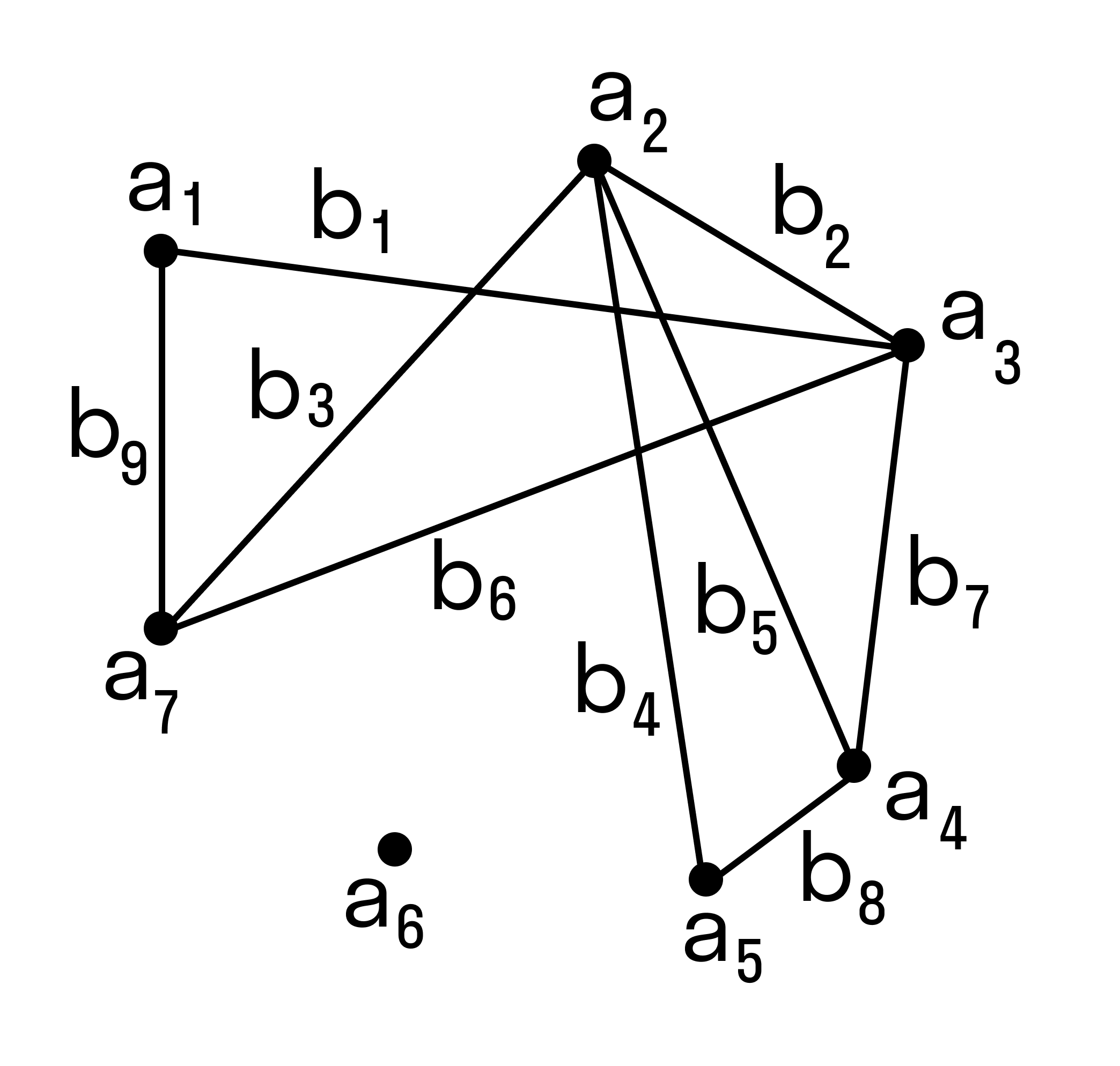
Графом называется система объектов произвольной природы (вершин) и связок (ребер), соединяющих некоторые пары этих объектов.
Пусть V — (непустое) множество вершин, элементы v ∈ V — вершины. Граф G = G(V) с множеством вершин V есть некоторое семейство пар вида: e = (a, b), где a, b ∈ V, указывающих, какие вершины остаются соединёнными. Каждая пара e = (a, b) — ребро графа. Множество U — множество ребер e графа. Вершины a и b — концевые точки ребра e.
Широкое применение теории графов в компьютерных науках и информационных технологиях можно объяснить понятием графа как структуры данных. В компьютерных науках и информационных технологиях граф можно описать, как нелинейную структуру данных.
Линейные структуры данных особенны тем, что связывают элементы отношениями по типу «простого соседства». Линейными структурами данных можно назвать массивы, таблицы, списки, очереди, стеки, строки. В нелинейных структурах данных элементы располагаются на различных уровнях иерархии и подразделяются на три вида: исходные, порожденные и подобные.
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:Как связать угол тента и затеняющей сетки. Навыки вязания узлов.Скачать
Основные понятия теории графов
Граф — это геометрическая фигура, которая состоит из точек и линий, которые их соединяют. Точки называют вершинами графа, а линии — ребрами.
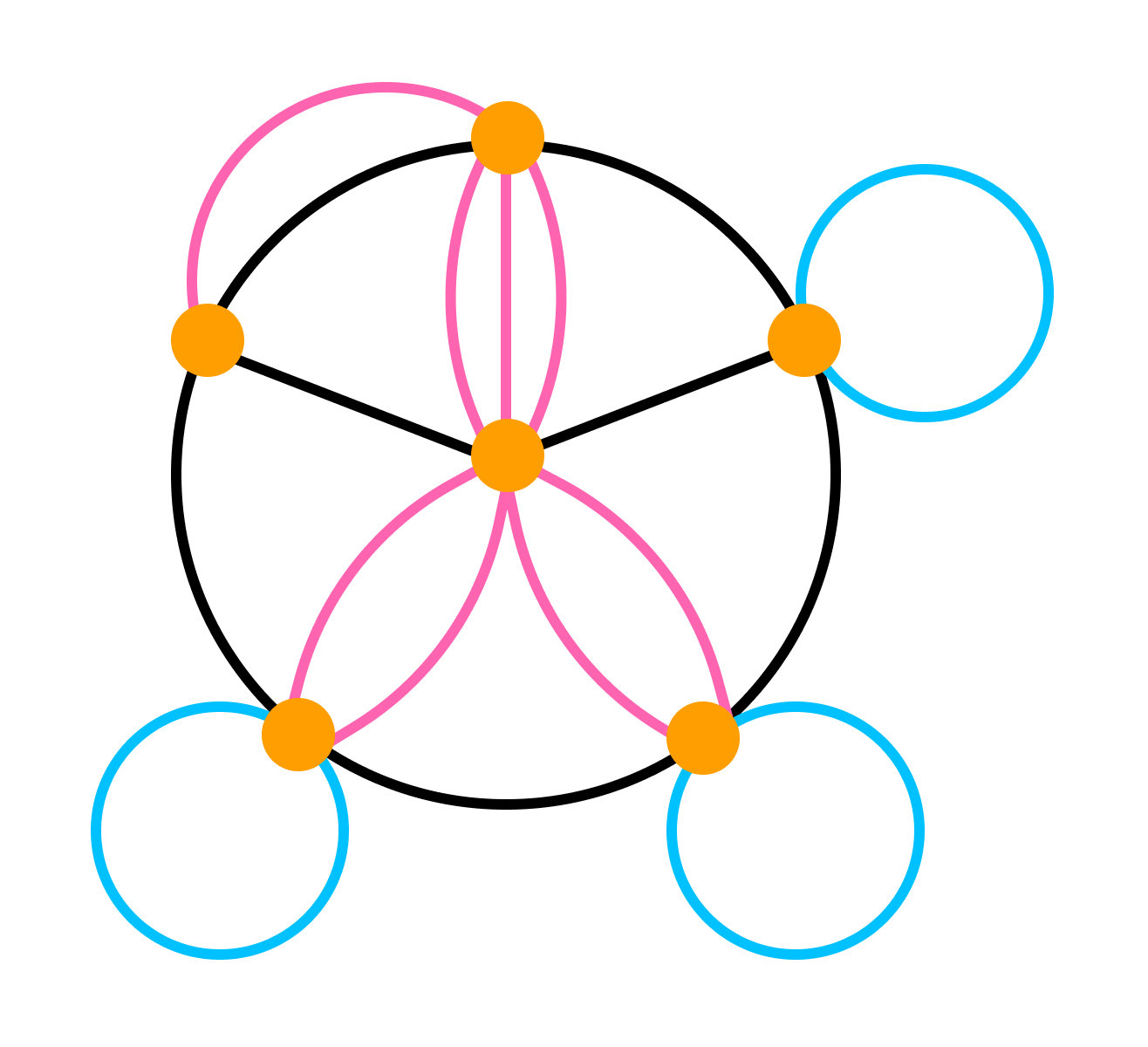
- Два ребра называются смежными, если у них есть общая вершина.
- Два ребра называются кратными, если они соединяют одну и ту же пару вершин.
- Ребро называется петлей, если его концы совпадают.
- Степенью вершины называют количество ребер, для которых она является концевой (при этом петли считают дважды).
- Вершина называется изолированной, если она не является концом ни для одного ребра.
- Вершина называется висячей, если из неё выходит ровно одно ребро.
- Граф без кратных ребер и петель называется обыкновенным.
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Глава 2. Сколько узлов на отрезке?
Применение формулы Пика для вычисления площадей некоторых фигур не совсем удобно. Очень уж чётким должен быть чертёж и очень внимательно нужно его рассматривать, чтобы определить, лежит ли данный узел внутри фигуры или же попал на её границу. Как точно сосчитать число узлов на границе? Поскольку граница состоит из отрезков, то нас интересует количество узлов сетки, лежащих на произвольном отрезке с концами в узлах.
Сделаем сначала небольшое наблюдение. Пусть А и В – узлы сетки. Обозначим через С 
первый узел, встречавшиеся после А на отрезке АВ (значит, между А и С больше нет узлов). Построим прямоугольный треугольник А СD с гипотенузой А С и катетами, лежащими на линиях сетки (рис.1).
Если С ≠ В, то сместим этот треугольник вдоль
отрезка АВ на расстояние А С. Получим равный
ему треугольник СС
D.
Следовательно, С – узел, и между С и Снет узлов. Ясно,
что если эту процедуру продолжить, мы когда-нибудь
получим в качестве очередной точки С 
точку В – узел
сетки. Рассматривая большой прямоугольный треугольник
ARB с гипотенузой АВ, приходим к равенствам: Рис. 1
AR = (k+1) · AD,
BR = (k+1) · СD , (1)
AB = (k+1) · A С
Теперь мы можем выяснить, сколько узлов Рис. 2. лежит между точками А и В(конечно, мы считаем, что А и В не лежат на одной линии сетки). Построим прямоугольный треугольник ARB с вершинами в узлах сетки и с гипотенузой АВ (рис.2).
Пусть AR = р, BR = q. Понятно, что р и q – целые положительные числа.
Теорема. Если р и q взаимно просты, то между А и В на отрезке АВ нет узлов сетки. Если же наибольший общий делитель р и q равен n , где n > 1 (НОД (р, q ) = n > 1), то на отрезке АВ между точками А и В расположены ровно ( n – 1) узлов сетки.
Доказательство. 1) Пусть числа p и q взаимно просты. Если между А и В были k узлов (k ≥ 1), то, взяв ближайший к А узел С, мы получим по формулам (1): p =(k+1) · AD, q = (k +1) · СD, то есть р и q имеют общий делитель k + 1, больший 1. Но ведь они взаимно просты!
2)Пусть НОД (р,q) = n > 1. Поделив отрезки AR и BR на n равных частей, мы опять приходим к рис.1, где С, С, …, С – какие-то узлы сетки и k=n – 1. Таким образом, в этом случае между точками А и В есть хотя бы n – 1 узел. Почему их не может быть больше, чем n – 1? В этом случае между узлами А и С были бы и другие узлы. Пусть С – ближайший к А узел. Тогда АС´ Задача 1. [11] В прямоугольнике 4×7, нарисованном на клетчатой бумаге, провели диагональ. Сколько клеточек она разрезала?
Задача 2. В прямоугольнике размером 200×300, нарисованном на клетчатой бумаге, провели диагональ. Сколько клеточек она разрезала на две части?
З
адача 3. В прямоугольнике 1000×1003, нарисованном на клетчатой бумаге, провели диагональ. Сколько клеточек она разрезала?
Задачу 1 легко решить, просто «водя пальцем по картинке»
Для решения задачи 2 полезно вспомнить наши разговоры о количестве узлов на отрезке и обсуждение
рис.1: ясно, что вдоль диагонали прямоугольника 200×300 можно расположить 100 прямоугольников 2×3, и в каждом из них, очевидно, диагональ будет рассекать по 4 клетки. Поэтому ответ к задаче 2 – четыреста клеток.
В задаче 3 такие соображения, увы, не помогают: числа 1000 и 1003 взаимно не просты. Сформулируем эту задачу в общем виде:
Сколько клеток рассекает на две части диагональ прямоугольника m×n, где m и n – взаимно простые числа?
Заметим, что диагональ такого прямоугольника не проходит через узлы. Будем считать, что диагональ идёт из левого нижнего угла прямоугольника. Самой первой она рассекает левую нижнюю угловую клетку (клетку № 1), потом она попадёт в клетку № 2 (рис.4), и так далее. Пусть диагональ уже пересекла k клеток. Так как она ни разу не проходит через узел, то всегда можно однозначно указать, какую клетку она рассечёт после клетки с номером k.
Итак, мы получили «цепочку», идущую из левого нижнего угла в правый верхний. Нам надо понять,
Рис. 4 чему равно число клеток в этой цепочке. Дадим каждой клетке адрес (t, s), если она расположена в горизонтальном ряду с номером t и вертикальном ряду с номером s. Левый нижний угол получает адрес (1,1), а правый верхний – (m,n). Теперь остаётся заметить, что при переходе от клетки с номером k в нашей цепочке к клетке с номером k+1 сумма чисел t и s в адресе возрастает точно на 1. Значит,
чтобы перейти от клетки с адресом (1,1) к клетке с адресом (m,n), надо сделать ровно m + n – 2 шагов, пройдя, таким образом, m + n – 1 клеток.
Итак, ответ к задаче 3 – число клеток равно 2002.
Объединим задачи 2 и 3.
Пусть m и n – произвольные натуральные числа.
Сколько клеток рассекает диагональ
Пусть d = НОД (m×n). Как и при решении задачи 2,
мы видим, что вдоль диагонали исходного
прямоугольника образуется d маленьких прямоугольников 
. Стороны этих маленьких прямоугольников уже взаимно просты, поэтому их диагонали рассекают по + – 1 клеток каждая. Значит, диагональ исходного прямоугольника рассечёт ( + – 1) · d = m + n – d клеток.
Теперь при желании мы можем без труда сосчитать, сколько клеток рассекут диагонали следующих прямоугольников: 36×56, 105×24, 2003×111.
Глава 3. Задачи на разрезание
С этими задачами, очевидно, столкнулся ещё первобытный человек, когда пытался раскроить шкуру убитого зверя, чтобы сшить себе одежду. Известно, что решения многих простых задач на разрезание были найдены ещё древними греками. Первый письменный источник с подобными задачами относится к Х веку – это фрагменты трактата персидского астронома Абул-Вефа, жившего в Багдаде. Профессиональные математики всерьёз занялись задачами на разрезание ближе к середине XIX века.
Сделаем небольшую классификацию таких задач [15]. Все их сюжеты можно условно поделить на следующие виды и подвиды:
* Дробление – требуется разрезать данную фигуру:
на заданное число равных между собой, или, как говорят математики, — конгруэнтных частей (фигур);
на заданное число конгруэнтных и подобных ей фигур (такие фигуры получили название «делящихся»);
определённым количеством прямых на максимально возможное число частей, не обязательно равных.
Возможны и другие вариации условий разрезания, так как фантазия человека не имеет ограничений.
* Квадрирование – разрезание фигуры на возможно меньшее число частей, из которых затем можно сложить квадрат.
* Трансформирование – требуется разрезать одну фигуру так, чтобы их её частей можно было сложить вторую заданную фигуру (не квадрат).
В отдельный подвид можно выделить очень популярные задачи на разрезание шахматной доски, которые отличаются от остальных задач на разрезание тем, что на доске есть раскраска квадратов, и это накладывает дополнительные требования при поиске решения.
Учитывая большое общее количество задач на разрезание, мы в этой работе будем рассматривать задачи на клетчатой бумаге на дробление и задачи, связанные с шахматной доской. А остальные постараемся изучить при дальнейшем исследовании по этой теме.
Следует учесть, что термин «разрезание» не всегда надо понимать буквально: при решении приведённых далее задач достаточно на чертеже данной фигуры обозначить линии разреза карандашом. Но смысл разрезания предполагает ещё и выход из плоскости и переворачивание фигуры любой её стороной из двух существующих.
В качестве примеров рассмотрим несколько типичных задач на разрезание, которые встречаются во многих сборниках занимательных задач и одну менее известную задачу на делящиеся фигуры, которая представляет собой небольшое исследование.
Задача 1 . Можно ли разрезать квадрат 66 на полоски 14 ?
Р
ешение. Используем раскраску, показанную на рис. 1. Любая полоска 14, положенная на такую доску, покроет ровно одну чёрную клетку. Следовательно, если бы мы разрезали квадрат на полоски, то чёрных клеток оказалось бы столько же, сколько полосок. Но число полосок должно быть равно (6 · 6) : 4 = 9, а чёрных клеток на этом рисунке 8! Значит разрезание
Рис. 1 невозможно.
Вместо раскраски в два цвета можно было использовать раскраску в четыре цвета, изображённую на рисунке 2 (каждый цвет помечен своим номером: цвет 1, цвет 2, цвет 3 и цвет 4). Рис. 2
Тогда каждая полоска 14 будет содержать ровно по одной клетке каждого цвета. Значит, если бы удалось разрезать квадрат на полоски, то клеток всех цветов было бы поровну. Но клеток цветов 1 и 3 – по 9, цвета 2 – 10, а цвета 4 – 8 штук.
Теперь вы сможете самостоятельно решить задачи 2 и 3.
Задача 2. Можно ли прямоугольник 89 разрезать на полоски 16 ?
Задача 3. Можно ли сложить прямоугольник из нарисованных на рис. 3 фигурок? (Каждая фигурка должна использоваться ровно один раз!)
З
адача 4. [8] На шахматной доске стоят 4 коня (рис. 4) Требуется разделить доску на 4 одинаковые по форме части, на каждой из которых стоял бы в точности один конь
Рис. 4 Задача 5 . [3] В Волшебной Стране свои волшебные законы природы, один из которых гласит: «Ковёр-самолёт будет летать только тогда, когда он имеет прямоугольную форму». У Ивана-царевича был ковёр-самолёт размером 912. Как-то раз Змей Горыныч подкрался и отрезал от этого ковра маленький коврик размером 18. Иван царевич очень расстроился и хотел было отрезать ещё кусочек 14, чтобы получился прямоугольник 812, но Василиса Премудрая предложила поступить по-другому. Она разрезала ковёр на три части, из которых волшебными нитками сшила квадратный ковёр-самолёт размером 1010. Сможете ли вы догадаться, как Василиса Премудрая переделала испорченный ковёр?
Задача 6. [1] На прямоугольном участке земли находятся 4 колодца, изображённые на рис. 5 точками. Разбейте этот участок на 4 части, одинаковые по величине и форме, так, чтобы колодцы на каждом участке занимали одно и то же положение. Рис. 5
Задача 7. [15] Найти все целые положительные числа n таким образом, чтобы каждый треугольник можно было разрезать на n треугольников, подобных между собой.
Решение. Начертим разносторонний треугольник. Прежде всего покажем, как любой треугольник можно разрезать на n = k² равных (следовательно, подобных) треугольников, т.е. на число n, равное квадрату целого числа. Разделим каждую сторону треугольника на k равных частей и через точки деления проведём прямые, параллельные его сторонам. Тогда число малых треугольников равно 1+ 3 + 5 + … + (2k – 1) = k²
Рис. 6. k = 5, n = 25 Рис. 7 Рис. 8
Теперь покажем, что каждый треугольник разрезается на любое число n ≥ 4 подобных между собой треугольников.
В самом деле, оставим на рис. 6 малые треугольники только в нижней полосе (трапеции), а все остальные объединим в один (рис. 7).
Столь же легко показать, что число таких частей может быть сделано любым нечётным n ≥ 7 : верхний из четырёх треугольников разбит на 2k (k ≥ 2) частей, и ещё имеется три нижних, так что общее число частей равно n = 2k + 3, где k ≥ 2 (рис. 8).
Итак, любой треугольник можно разрезать на любое число n подобных между собой треугольников, за исключением n = 2, 3, 5. Можно доказать, что для этих значений n требуемое разрезание невозможно.
Вот именно с таких занимательных задач начинается уже серьёзная математика с исследованиями, доказательствами и построением небольшого раздела математической теории под названием «делящиеся фигуры на плоскости».
Задача 8. [16] «Парадокс шахматной доски»
Шахматная доска разрезается наискосок, как это изображено на левой половине рисунка 9, а затем часть В сдвигается влево вниз, как это показано на правой половине рисунка. Первоначальная площадь Рис. 9
равнялась 64 кв. ед, теперь же она равна 63. Куда исчезла одна недостающая квадратная единица?
Глава 4. Расстояние в «клетчатом» городе
С понятием расстояния мы сталкиваемся ежедневно. «Каково расстояние от дома до школы?», «Сколько километров от Москвы до Петербурга?» — эти вопросы никого не удивят. Зная расстояние, мы можем прикинуть, долго ли добираться от одного места до другого. Все мы умеем вычислять расстояние между двумя точками на координатной прямой, с помощью теоремы Пифагора мы можем вычислить расстояние между двумя точками на координатной плоскости.
А теперь возьмём хорошо знакомый нам листок клетчатой бумаги и представим себе, что это – город, линии сетки – улицы. Давайте прогуляемся по этому городу, ходя только по улицам (порядки в этом городе очень строгие). Длину клетки будем считать равной 1. Как нам быстрее всего попасть с перекрёстка А на перекрёсток Б (рис. 1)?
Можно, например, пройти из А в С, а потом – из С в В. Можно было идти через D, а можно – и более замысловатым путём. Что же мы теперь назовём расстоянием от А до В? Конечно, длину кратчайшего
Рис. 1 пути: 4 + 3 = 7.
А теперь представим себе, что у нас в запасе есть время проделать путь длиной 3. В каких узлах мы можем побывать, выйдя из А? (Или: из каких узлов можно добраться до А, пройдя путь не более 3?) Ответ на этот вопрос изображён на рисунке 2). Наверное, многие из вас сейчас вспомнили о круге на плоскости: ведь круг радиуса r с центром в точке А и есть множество всех точек плоскости, которые удалены от А не больше, чем на r. Но как не похож ромбик из точек с рисунка 2 на привычный круг! Рис. 2
Познакомимся поближе с расстоянием в «клетчатом» городе с помощью нескольких задач.
Задача 1. [11] В «клетчатом» городе выделили район – квадрат 44. Какое
Наименьшее количество детских площадок нужно построить в этом районе, чтобы из любого узла этого района можно было попасть на одну из этих площадок, проделав путь не более 3?
Р
ешение. Понятно, что двух площадок хватает (рис. 3). Ещё легче понять, что одной площадки будет мало (слишком далеко разбросаны узлы, находящиеся на границе квадрата!)
Решите такую же задачу с прямоугольником 63. А как решается подобная задача, если расстояние на плоскости измеряется обычным способом?
Задача 2. Какое наибольшее количество котов можно разместить в узлах сетки на территории квадрата 44, чтобы расстояние между любыми двумя из них было не менее 2 (иначе коты подерутся)?
Наверное, без особого труда сумеете поделить территорию квадрата между 13 котами (рис. 4). А вот Рис. 4
14 котов мирно ужиться на этой территории уже не смогут. Докажем это. Поделим всю территорию, кроме центра квадрата, на 4 непересекающиеся зоны (рис. 5). Если даже одного из 14 котов поселить в центре квадрата, то остальных 13 придётся разместить по этим зонам. Значит, в какой-то зоне окажется хотя бы 4 кота. Перебирая различные варианты расселения 4 котов в
Рис. 5 какой-нибудь из этих зон, легко увидеть, что это невозможно.
Подумайте, как решить эту задачу, если расстояние на плоскости измеряется, как обычно.
Итак, мы познакомились с расстоянием в «клетчатом» городе. Оно ни чуть не менее естественно, чем обычное расстояние «по прямой». Что их объединяет? Каковы общие свойства, которыми должно обладать расстояние?
Свойство 1. Расстояние между двумя точками неотрицательно, причём оно равно нулю, только если точки совпадают.
Ещё бы! Чтобы попасть из точки А в неё же, никуда идти не надо, а чтобы попасть в другую точку В, придётся проделать некий путь положительной длины.
Свойство 2. Расстояние от точки А до точки В равно расстоянию от точки В до точки А.
Недаром мы говорим обычно не о расстоянии от А до В, а о расстоянии между А и В, не различая расстояния от А до В и от В до А.
Свойство 3. Для точек А, В и С сумма расстояний от А до С и от С до В не меньше расстояния от А до В (неравенство треугольника).
Свойства 1, 2 и 3 в математике называются аксиомами расстояния. Как мы знаем, эти свойства есть у обычного расстояния на плоскости. Не трудно проверить, что есть они и у нового расстояния, введённого нами в «клетчатом» городе.
Глава 5. Игры на клетчатой бумаге
1. Крестики — нолики
1. Популярная игра в крестики – нолики состоит в следующем. Двое по очереди рисуют на листе клетчатой бумаги крестики и нолики. Первый игрок рисует крестики, второй – нолики. Выигрывает тот, кто первым поставит определённое количество своих знаков в ряд (по вертикали, горизонтали или диагонали). Следующая задача относится к этой игре.
Задача. [4] Докажите, что при игре в крестики – нолики второй игрок, как бы хорошо он ни играл, не может рассчитывать больше, чем на ничью, если его партнёр играет правильно.
2. Бридж-ит («перебрось мостик!»)
Н
а рисунке показана доска для игры в бридж-ит. Участники игры по очереди проводят вертикальные или горизонтальные линии, соединяющие две соседние точки «своего» цвета: один игрок соединяет синими линиями синие точки, другой – чёрными линями чёрные точки. Линии противников нигде не должны пересекаться. Выигрывает тот, кто первым построит ломаную, соединяющую две противоположные стороны доски «своего» цвета. Так на рисунке выиграли «синие». В этой игре у начинающего игру есть выигрышная стратегия.
Когда вы вдоволь наиграетесь с друзьями в эту игру, можете либо придумать стратегию, либо прочитать о ней в книге М. Гарднера «Математические досуги»
Д
ля игры в солитер нужны игровое поле-доска из 33 клеток и фишки, шашки или монетки. Игра начинается с того, что на все клетки доски, кроме центральной, расставляются фишки. Цель игры состоит в том, чтобы после ряда «прыжков» на доске осталась всего одна фишка. «Прыжок» означает следующее: фишка переносится на свободную клетку через любую соседнюю фишку, которая при этом снимается с доски, причём фишки могут прыгать влево, вправо, вверх и вниз (но не по д
иагонали!). Каждый ход обязательно должен быть прыжком через фишку. Если очередной ход невозможен, то игра заканчивается.
Прежде чем играть в солитер, можете решить несколько более простых задач из книги М. Гарднера «Математические досуги».
4
. Жизнь [11]
Эту игру придумал математик Дж. Конуэй. В неё можно играть одному. Для игры вам понадобится большая доска, разграфленная на клетки, и много плоских фишек двух цветов. Основная идея игры состоит в том, чтобы, начав с какого-нибудь простого расположения фишек, расставленных в разных клетках, проследить за эволюцией исходной позиции под действием «генетических законов» Конуэя, которые управляют рождением, гибелью и выживанием фишек. Вот эти законы.
1. Выживание. Каждая фишка, имеющая две или три соседние фишки, выживает и переходит в следующие поколения. (Соседние фишки – те, которые расположены на соседних клетках: смежных по горизонтали, вертикали или диагонали.)
2. Гибель. Каждая фишка, у которой больше трёх соседей, погибает (то есть снимается с доски) из-за перенаселённости. Каждая фишка, вокруг которой свободны все соседние клетки или занята всего одна клетка, погибает от одиночества.
3. Рождение. Если число фишек, с которыми граничит какая-нибудь пустая клетка, в точности равно трём, то на этой клетке происходит рождение нового «организма», то есть следующим ходом на неё ставится одна фишка.
Важно понять, что гибель и рождение всех «организмов» происходят одновременно. Вместе взятые, они образуют одно поколение – один «ход» в эволюции. Чтобы не запутаться, ходы рекомендуется делать так:
1) начать с конфигурации, целиком состоящей из чёрных фишек;
2) определить, какие фишки должны погибнуть, и положить на каждую из обречённых фишек по одной чёрной фишке;
3) Найти все свободные клетки, на которых должен произойти акт рождения, и на каждую из них поставить по одной белой фишке;
4) Всё проверить, затем снять с доски все погибшие фишки (столбики), а всех новорождённых (белые фишки) заменить чёрными фишками.
Вы получите новое поколение. Дальше действуйте аналогично. Вы обнаружите много интересного и красивого в эволюции семейств организмов.
Глава 6. Интересные факты
В этой главе мы приведём без доказательства несколько интересных и красивых фактов, относящихся к клетчатой плоскости. В основном, это довольно трудные теоремы. Но мы надеемся, что они понравятся вам так же, как нам, и у вас тоже возникнет желание продолжить знакомство с клетчатой плоскостью.
Факт 1. Пусть выпуклый многоугольник имеет площадь больше 4 и начало координат является его центром симметрии. Тогда этот многоугольник содержит ещё хотя бы одну точку с целыми координатами. ( Теорема Минковского) .
Рис. 1 Эта теорема верна не только для выпуклых многоугольников, но и для выпуклых фигур – фигур, которые с любой парой своих точек содержат и весь отрезок с концами в этих точках. Например, круг и эллипс – выпуклые фигуры, а кольцо – нет.
Смысл этой теоремы состоит в том, что выпуклая фигура, «набирая» площадь 4, не сможет «избежать» захвата узлов сетки. Понятно, что для невыпуклых фигур это не так: они могут «набирать» площадь, «обходя» узлы сетки (рис. 1).
Факт 2. Пусть внутри выпуклой фигуры площади S и периметром 2р лежит узлов решётки. Тогда n > S – р. [10]
Смысл этого факта таков: если мы захотим оградить на клетчатом листке участок (выпуклый) достаточно большой площади и мы сделаем это, «экономно» расходуя ограду, то на участке окажется довольно много узлов сетки. Если же мы будем расходовать ограду «неэкономно», сильно вытягивая участок, то узлов на участке может оказаться не так много.
Кстати, задача о нахождении фигуры наибольшей площади, имеющей данный периметр, давно волновала математиков. Её назвали изопериметрической задачей. Такой фигурой является круг: из всех фигур с данным периметром самую большую площадь и
меет он. (рис. 2 и 3)
Величина S – р велика. Площадь мала, а периметр велик.
Узлов много! Узлов нет!
Факт 3. Если вершины выпуклого n-угольника лежат в узлах клетчатой бумаги, а внутри и на его сторонах других узлов нет, то n ≤ 4.
Иными словами, вам ни за что не удастся (попробуйте сами!) нарисовать на клетчатой бумаге выпуклый пяти-, шести-, и т.д. многоугольник с вершинами в узлах сетки так, чтобы ни на его сторонах, ни внутри не было
Рис. 4 других узлов. А вот треугольник или четырёхугольник с таким свойством нарисовать совсем нетрудно!
Конечно, невыпуклые пяти-, шести-, и т.д. многоугольники с таким свойством тоже можно нарисовать (рис. 4).
Факт 4. Из правильных многоугольников только четырёхугольник (квадрат) можно разместить на клетчатом листе так, чтобы все его вершины лежали в узлах сетки. Ни с правильным треугольником, ни с правильным пятиугольником, и т. д., этого сделать нельзя! [2]
(Напомним, что правильным называется многоугольник, у которого все стороны и все углы равны).
Заметим, что квадрат с удобством размещается на клетчатой плоскости не только очевидным образом (когда его стороны Рис. 5
идут по линиям сетки), но и иначе (рис. 5).
В процессе исследования мы изучили много справочной, научно-популярной литературы, побывали на сайтах, вызывающих уважение и некоторое благоговение: малый Мехмат МГУ, ФИПИ, прочитали некоторые книги в электронном виде. Мы рассмотрели различные задачи на построение и вычисления, заданные на клетчатой бумаге, научились применять решение таких задач в различных областях математики, подобрали нестандартные задания. Эти задачи отличаются от обычных задач, изложенных в действующих учебниках и задачниках по математике.
Любители головоломок увлекаются решением задач на клетчатой бумаге, прежде всего потому, что универсального метода решения таких задач не существует, и каждый, кто берётся за их решение, может в полной мере проявить свою смекалку, интуицию и способность к творческому мышлению. Поскольку здесь не требуется глубокое знание геометрии, то любители иногда могут даже превзойти профессионалов-математиков.
Вместе с тем, задачи на клетчатой плоскости не являются несерьёзными или бесполезными, они не так уж и далеки от серьёзных математических задач. Из задач на разрезание родилась теорема Бойаи-Гервина о том, что любые два равновеликих многоугольника равносоставлены (обратное очевидно). Задача на нахождение площади многоугольника с вершинами в узлах сетки сподвигла австрийского математика Пика в 1899 году доказать замечательную формулу Пика.
В результате нашей работы мы расширили свои знания о решении задач на клетчатой бумаге, определили для себя классификацию исследуемых задач, убедились в их многообразии.
Мы научились вычислять площади многоугольников, нарисованных на клетчатом листке, встретились с совсем новыми, необычными «расстояниями», узнали, как раскраска клеточек помогает решать многие задачи, познакомились поближе с задачами на разрезание и, наконец, научились играть в увлекательные игры на листке бумаги в клетку.
Рассмотренные нами задания имеют различный уровень трудности – от простых до олимпиадных. Каждый может найти среди них задачи посильного уровня сложности, отталкиваясь от которых, можно будет переходить к решению более трудных.
Работа по данной теме позволила нам преодолеть психологический барьер и поверить в свои силы, что является важнейшим фактором успешного решения олимпиадных и экзаменационных задач, выступления перед аудиторией с теоретическим материалом по математике.
Мы пришли к выводу, что тема, которая нас заинтересовала, достаточно многогранна, задачи на клетчатой бумаге многообразны, методы и приёмы их решения также разнообразны. Поэтому наша исследовательская группа решила продолжить работу в этом направлении: особенно интересными показались нам задачи на разрезание, «раскраски», задачи на трансформирование, пентамино, разрезание в пространстве. Мы решили составить сборник игр на клетчатой бумаге, которые не только увлекательны и интересны, но и развивают комбинаторно-геометрические навыки, интуицию, воображение.
Список используемой литературы
1. Болотин И. Б., Добрышина Л. Ф. Смоленские математические олимпиады школьников (готовимся к ЕГЭ). Смол. гос. ун-т; Смоленск: СмолГУ, 2008.
2. Геометрия на клетчатой бумаге. Малый МЕХмат МГУ. Режим доступа: /archive/20082009/KanunnikovKuznetsov/2.html
3. Григорьева Г. И . Подготовка школьников к олимпиадам по математике: 5 – 6 классы. Метод. пособие. – М.: Глобус, 2009.
4. Дынкин Е. Б., Молчанов С. А., Розенталь А. Л . Математические соревнования. Арифметика и алгебра. – М.: Наука, 1970.
5. Екимова М. А. ,Кукин Г. П. Задачи на разрезание. М.: МЦНМО, 2002. Режим доступа: /lib/files/pdf/kukin.pdf
6. Жарковская Н. М., Рисс Е. А . Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25.
7. Задачи открытого банка заданий по математике ФИПИ, 2010 – 2011. Режим доступа: /or/ege/ShowProblems.html?posMask=32
8. Игнатьев Е. И . В царстве смекалки. – М.: Наука, 1982.
9. Кенгуру – 2010. Задачи, решения, итоги. Режим доступа: /load
10. Прасолов В. В . Задачи по планиметрии. – М.: МЦНМО, 2000.
11. Рисс Е. А . Математический клуб «Кенгуру» Выпуск № 8 (изд. второе). – Санкт-Петербург, 2009.
12. Смирнова И. М., Смирнов В. А . Геометрия на клетчатой бумаге. – М.: Чистые пруды, 2009.
13. Смирнова И. М., Смирнов В. А . Геометрические задачи с практическим содержанием. – М.: Чистые пруды, 2010.
14. Смирнов В. А. ЕГЭ. Математика. Задача В6. Планиметрия. Р/т. – М.: МЦНМО, 2011.
15. Трошин В. В. Занимательные дидактические материалы по математике. Сборник заданий. Выпуск 2. – М.: Глобус, 2008.
16. Гарднер М. Математические чудеса и тайны. – М.: Наука, 1986.
📹 Видео
Как правильно плести сеть для раколовки (подсака, садка) по кругуСкачать
Расчет и метод посадки рыбацких сетей (рамованая)Скачать
Пифагория. Тема 10. ОкружностиСкачать
Интуитивная теория узлов | примеры нетривиальных узлов, задачи теории узлов, операция связной суммы.Скачать
Обзор схватывающих узлов. Все про схватывающие узлы.Скачать
