В единичном кубе abcda1b1c1d1 найдите длину вектора ab ad1

Сумма векторов

В кубе назовите вектор, равный сумме $overrightarrow+overrightarrow <B_C_>+overrightarrow<DD_> $

Вектор в пространстве

Установите соответствие между выражением и вектором $Х$

Длина вектора

Дано: АВ = 3 ВС = 4 СС₁ = 12

Длина вектора АС₁ =

Длина вектора

Диагонали параллелепипеда пересекаются в точке О.

Варианты ответа (введите порядковый номер):

Вектор в пространстве

Упростите выражение и выберите правильный результат преобразования:

Вектор в пространстве

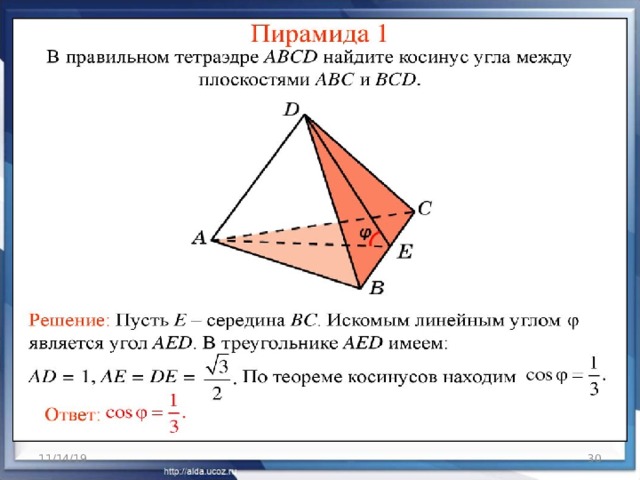
В тетраэдре ABCD точка Е — середина АD.

Докажите, что $overrightarrow=frac(overrightarrow+overrightarrow)$

Так как $overrightarrow+overrightarrow=0$, то $overrightarrow+overrightarrow=2overrightarrow$, значит $overrightarrow=frac(overrightarrow+overrightarrow)$

Сложим полученные равенства $overrightarrow+overrightarrow+overrightarrow+overrightarrow=2overrightarrow$

Видео:егэ векторы решу егэ все задания №2 профильСкачать

Подготовка к ЕГЭ

Разновидности стереометрических задач .

Просмотр содержимого документа
«Подготовка к ЕГЭ»

ПОДГОТОВКА К ЕГЭ. СТЕРЕОМЕТРИЧЕСКАЯ ЗАДАЧА(№14).

Работа учителя математики

Разновидности стереометрических задач.

• Расстояние от точки до прямой и до плоскости .
• Расстояние между прямыми и плоскостями .
• Угол между скрещивающимися прямыми .
• Угол между прямой и плоскостью .
• Угол между плоскостями .
• Задача на доказательство и вычисление .
• Сечения многогранников .
• Объёмы многогранников .
• Круглые тела: цилиндр, конус, шар.

Расстояние от точки до прямой.

• Расстояние от точки до прямой , не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую.
• Расстояние между двумя параллельными прямыми равно длине отрезка их общего перпендикуляра.
• Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой .

В единичном кубе ABCDA ₁B₁C₁D₁ найти расстояние от точки D₁ до прямой PQ,

где P и Q – середины соответственно

В единичном кубе ABCDA ₁B₁C₁D₁ найти расстояние от точки С до прямой ВД1.

Дано: АВСДА 1 В 1 С 1 Д 1 – куб. АВ = 1. Найти: Расстояние от точки С до прямой ВД 1 .

1. ∆ВСД 1 – прямоугольный ( по теореме о трёх

перпендикулярах), ∠Д 1 СВ – прямой .

2. СН – высота ∆ВСД 1 , значит СВ – среднее

пропорциональное между ВН и ВД 1 , тогда

СН – расстояние от точки С до прямой ВД 1 , поэтому СН – высота треугольника ВСД 1 . СН = 2·S ∆ВСД 1 : ВД 1 .

∆ Д 1 СВ – прямоугольный, т.к. Д 1 С  СВ

по теореме о трёх перпендикулярах .

Расстояние от точки до плоскости .

• Расстояние от точки до плоскости , не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этого точки на плоскость.
• Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.
• Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.
• Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра.
• Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.

• В единичном кубе ABCDA₁B₁C₁D₁ найдите расстояние от точки C₁ до плоскости AB₁C.

• В правильной треугольной призме АВСА1В1С1–все рёбра равны 1.Найдите расстояние от точки А до плоскости (ВСА1)

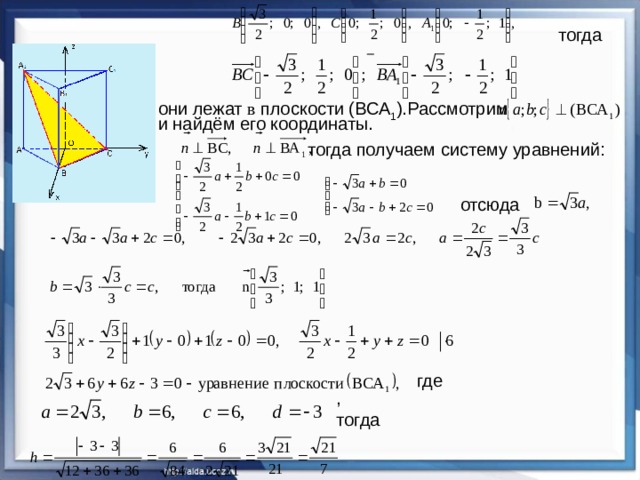
Дано: АВСА 1 В 1 С 1 – правильная треугольная призма, все рёбра равны 1. Найдите: Расстояние от точки А до плоскости (ВСА 1 )

Решение: h – расстояние от точки А до плоскости (ВСА 1 ),

поэтому h – высота пирамиды АВСА 1

с основанием ВСА 1 . h =

. Пусть основанием пирамиды будет ∆АВС,

тогда её высота – АА 1 .

∆ ВСА 1 – равнобедренный, А1К – его высота, тогда

За страницами учебника Расстояние от точки А до плоскости можно вычислить по формуле:

они лежат в плоскости (ВСА 1 ).Рассмотрим

и найдём его координаты.

тогда получаем систему уравнений:

Расстояние между прямыми и плоскостями .

• Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми. Общий перпендикуляр к двум скрещивающимся прямым существует и единственен.

Дано: АВСДА 1 В 1 С 1 Д 1 – куб. Все его рёбра равны 1. Найти: расстояние между прямыми АВ 1 и ВС 1 .

следовательно расстояние между скрещивающимися

прямыми ВС 1 и АВ 1 равно расстоянию между

соответствующими плоскостями. Диагональ СА 1

перпендикулярна этим плоскостям.

СА 1 ∩ (ВДС 1 ) = F;

CА 1 ∩ (АД 1 В 1 ) = Е.

EF – расстояние между ВС 1 и АВ 1 .

В ∆ АСЕ отрезок ОF ║ АЕ и проходит через середину отрезка АС, следовательно ОF – средняя линия треугольника АСЕ и, значит, ЕF = FC. Аналогично, О 1 Е – средняя линия треугольника А 1 С 1 F

Расстояние между скрещивающимися прямыми можно найти по формуле:

Дано: АВСДА 1 В 1 С 1 Д 1 – куб. Все его рёбра равны 1. Найдите расстояние между прямыми АВ 1 и ВС 1 .

• SABCD – правильная четырёхугольная пирамида, все рёбра которой равны 1.Найдите расстояние между прямыми АS и ВС.

Дано: SABCD – правильная четырёхугольная пирамида, все рёбра которой равны 1. Найдите: Расстояние между прямыми АS и ВС.

Угол между прямой и плоскостью .

• Прямая и плоскость пересекаются , если они имеют одну единственную общую точку, которую называют точкой пересечения прямой и плоскости .
• Прямая перпендикулярна к плоскости , если она перпендикулярна к любой прямой, лежащей в этой плоскости.
• Проекцией точкиМна плоскость называется либо сама точка М , если М лежит в плоскости , либо точка пересечения плоскости и прямой, перпендикулярной к плоскости и проходящей через точку М , если точка М не лежит в плоскости .
• Проекцией прямойaна плоскость называют множество проекций всех точек прямой a на плоскость .
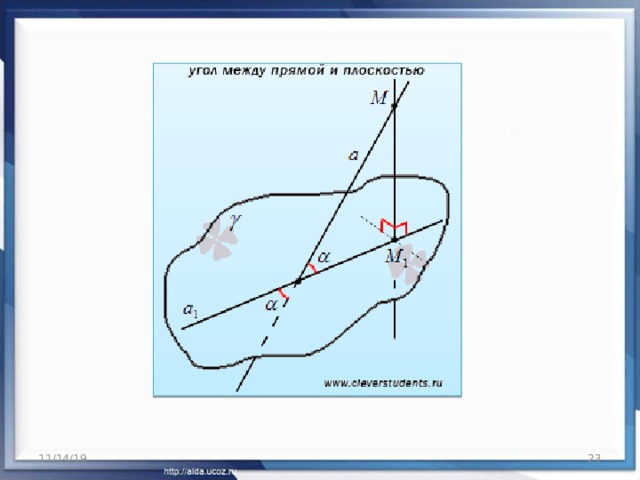
• Угол между прямой и плоскостью , пересекающей эту прямую и не перпендикулярной к ней, — это угол между прямой и ее проекцией на эту плоскость.
• Определение угла между прямой и плоскостью позволяет заключить, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми : самой прямой и ее проекцией на плоскость. Следовательно, угол между прямой и плоскостью есть острый угол.

На векторах построена пирамида. Найдите угол между прямой AD и плоскостью ABC .

• На векторах построена пирамида. Найдите угол между прямойADи плоскостьюABC .

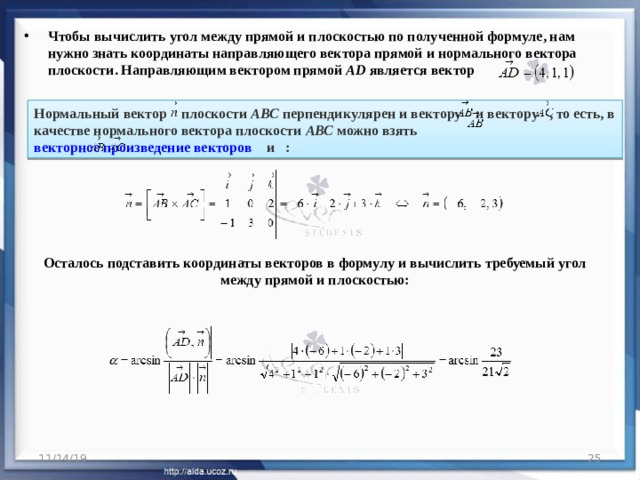
• Чтобы вычислить угол между прямой и плоскостью по полученной формуле, нам нужно знать координаты направляющего вектора прямой и нормального вектора плоскости. Направляющим вектором прямойADявляется вектор

Нормальный вектор плоскости АВС перпендикулярен и вектору и вектору , то есть, в качестве нормального вектора плоскости АВС можно взять векторное произведение векторов и :

Осталось подставить координаты векторов в формулу и вычислить требуемый угол между прямой и плоскостью:

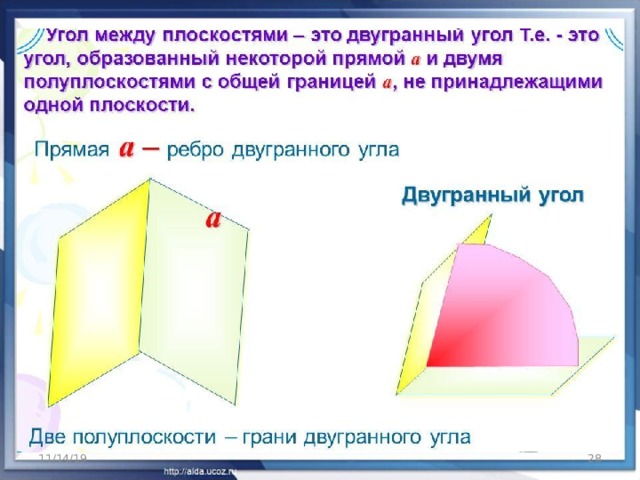
Угол между плоскостями .

Задача на доказательство и вычисление .

В конус, радиус основания которого равен 3, вписан шар радиуса 1,5.

а) Изобразите осевое сечение комбинации этих тел.

б) Найдите отношение площади полной поверхности конуса к площади поверхности шара.

В основании правильной треугольной призмы ABCA 1 B 1 C 1 лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A 1 C 1 .

а) Постройте сечение призмы плоскостью BAN .

б) Найдите периметр этого сечения.

См.сайт «Решу ЕГЭ»

Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.

Данный материал характеризуется следующим особенностями:

Метод сечений применяется только для многогранников, так как различные сложные (наклонные) виды сечений тел вращения не входят в программу средней школы.

В задачах используются в основном простейшие многогранники.

Задачи представлены в основном без числовых данных, чтобы создать возможность их многовариантного использования.

Чтобы решить задачу построения сечения многогранника ученик должен знать:

• что значит построить сечение многогранника плоскостью;
• как могут располагаться относительно друг друга многогранник и плоскость;
• как задается плоскость;
• когда задача на построение сечения многогранника плоскостью считается решенной.

Поскольку плоскость определяется:

построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.

Существует три основных метода построения сечений многогранников:

Метод следов. Метод вспомогательных сечений. Комбинированный метод.

Первые два метода являются разновидностями Аксиоматического метода построения сечений.

Можно также выделить следующие методы построения сечений многогранников:

построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;

• построение сечения, проходящего через заданную прямую параллельно другой заданной прямой;
• построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;
• построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;
• построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.

• В правильной четырёхугольной пирамидеMABCDс вершинойMстороны основания равны 1, а боковые рёбра равны 2. ТочкаNпринадлежит ребруMC,причёмMN: NC = 2:1.Найдите площадь сечения пирамиды плоскостью, проходящей через точкиBиNпараллельно прямойAC.
• См . сайт «Решу ЕГЭ»

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Решение типовых заданий ЕГЭ второй части — 1

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:№364. Точка К—середина ребра В1С1 куба ABCDA1B1C1D1. Разложите вектор АК по векторам а = АВ,Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

(типовые задания С2) — 1 Многогранники: виды задач и методы их решения Методическая разработка Амачкиной А.А. МОУ СОШ №12, г. Балашиха, Московской области.

Расстояние между точками A и B можно вычислить: 1) как длину отрезка AB , если отрезок AB удается включить в некоторый треугольник в качестве одной из его сторон; 2) по формуле 3) по формуле 1.1. Расстояние между двумя точками

Пример 1. В единичном кубе ABCDA1 B1 C1 D1 на диагоналях граней AD1 и D1 B1 взяты точки Е и F так, что Найти длину отрезка EF. Поэтапно-вычислительный метод

(треугольник AB1 D1 является равносторонним). Имеем

Пример 1. В единичном кубе ABCDA1 B1 C1 D1 на диагоналях граней AD1 и D1 B1 взяты точки Е и F так, что Найти длину отрезка EF. Векторный метод А А1 В1 В Е D С D1 С1 F

Решение. Введем прямоугольную систему координат Пример 2. В единичном кубе ABCDA1B1 C1 D1 точки E и K – середины ребер AA1 и CD соответственно, а точка M расположена на диагонали B1 D1 так, что B1 M = 2MD1. Найти расстояние между точками Q и L, где Q – середина отрезка ЕМ, а L – точка отрезка МК такая, что ML = 2LK. Координатный метод А E D C K x z Q M L А1 B1 C1 D1 B y

Для нахождения координат точки М используем формулу координат точки (опорная задача 1), делящей отрезок B1 D1 в отношении 2:1. Имеем Тогда Аналогично получим координаты точки L, делящей отрезок MK в отношении 2:1. Имеем

Координаты точки Q равны полусуммам соответствующих координат точек E и М, поэтому

Используемая литература: Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения. МАТЕМАТИКА ЕГЭ 2011 (типовые задания С2) Корянов А. Г., г. Брянск, akoryanov@mail.ru Прокофьев А.А., г. Москва, aaprokof@yandex.ru

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 945 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 679 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 302 человека из 66 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Задание 3 (№27717) ЕГЭ по математике. Урок 80Скачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 507 538 материалов в базе

Материал подходит для УМК

«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.

Глава 3. Тригонометрические уравнения

Другие материалы

• 08.04.2018
• 11119
• 41

• 04.04.2018
• 33786
• 1353

• 10.03.2018
• 326
• 0

• 05.03.2018
• 351
• 2

• 24.02.2018
• 406
• 1

• 19.02.2018
• 486
• 0

• 16.02.2018
• 5152
• 14

• 12.02.2018
• 421
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 13.04.2018 784
• PPTX 272.1 кбайт
• 1 скачивание
• Оцените материал:

Настоящий материал опубликован пользователем Амачкина Алла Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 4 года и 10 месяцев
• Подписчики: 1
• Всего просмотров: 23707
• Всего материалов: 26

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Длина вектора через координаты. 9 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Половина российских родителей не одобряют увлечение их детей просмотром видеоблогов

Время чтения: 2 минуты

Школы Пскова перевели на дистанционное обучение

Время чтения: 2 минуты

Студенты РФ и Великобритании подписали договор о создании студенческой Ассоциации

Время чтения: 1 минута

Минпросвещения намерено решить вопрос с третьей сменой в школах в 2023 году

Время чтения: 1 минута

В Госдуме предложили создать в школах «ящики доверия» для обращений к психологу

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🎥 Видео

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и В1D1. Ответ дайте в градусах.Скачать

№745. В прямоугольнике ABCD AB=3см, BC=4см, M-середина стороны AB.Скачать

№190. Дан куб ABCDA1B1C1D1. Найдите следующие двугранные углы: а) АВВ1ССкачать

№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

егэ векторы. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину суммы векторов АБ и АДСкачать

Диагонали изображенного на рисунке ромба ABCD равны 12 и 16. Найдите длину вектора АВ + АДСкачать

№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать

№330. Нарисуйте параллелепипед ABCDA1B1C1D1 и обозначьте векторы C1D1, BA1Скачать

№402. Даны координаты четырех вершин куба ABCDA1B1C1D1: А (0; 0; 0), В (0; 0; 1), D (0; 1; 0)Скачать

Как находить угол между векторамиСкачать

Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать

Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

№344. Диагонали куба ABCDA1B1C1D1 пересекаются в точке О. Найдите число k такое,Скачать