Метод обратных итераций для нахождения собственных векторов

Метод обратных итераций предназначен для поиска собственного вектора Хц когда соответствующее собственное значение А XjXj, находим

Поскольку система собственных векторов Xj, j = 1, . П линейно- независима, то (lj -i_f) -pj = 0, j =1. П , t. e.

Согласно формуле (6.23) один из коэффициентов разложения Cj велик при Xj = X_t. Это обстоятельство является решающим в методе обратных итераций. Уточним его для нескольких случаев.

Случай № L Пусть собственное значение Я, является простым, тогда среди коэффициентов разложения i =l. n , согласно (6.23) коэффициент ^ является большим, т. е. вектор X с точностью до нормировки близок вектору X;.

Таким образом, согласно (6.23) в методе обратной итерации собственный вектор отыскивается тем лучше, чем точнее известно соответствующее собственное значение. Если собственное значение известно слишком грубо или вектор Ь выбран неудачно так, что X и X, отличаются значительно, организуют итерационный процесс в следующем виде:

Расчеты показывают, что итерационный процесс сходится быстро (достаточно одной двух итераций), при этом на каждом шаге рекомендуется нор-

Случай № 2.11усть собственное значение X, является кратным р > 1 и ему соответствует р линейно-независимых собственных вектора Хц . Х_р. В этом случае векторы X], . Х_р определяются неоднозначно, т. к. любая их линейная комбинация является собственным вектором. Действительно, имеем следующую цепочку верных равенств

т. е. система векторов Хц . Х_р порождает подпространство, в котором можно выбрать произвольный базис. Векторы, составляющие выбранный базис, могут быть рассмотрены в качестве искомых собственных векторов.

В этом случае согласно (6.23), в разложении вектора X будут усилены несколько компонент ?ь 1 и ему соответствует q (q (ii) , соответствующих правым частям Ьц лишь q векторов являются линейно-независимыми, что выясняется при использовании процедуры ортогонализации.

Количество арифметических операций в методе обратных итераций скла-

дывается из нахождения собственного вектора * П операций, число же собственных векторов * п , т. е. всего « п’ 1 операций. Таким образом, при больших п метод неэкономичен, но при п небольших (в пределах нескольких сотен) он вполне приемлем, т. к. прост, универсален и устойчив.

В листинге 6.5 приведен код программы для поиска собственных векторов матрицы, у которой все собственные значения простые. Кроме того, собственные значения считаются известными, быть может, и с некоторой погрешностью. В качестве примера матрицы берется трехдиагональная матрица Q (6.18).

%Программа поиска собственных векторов матрицы %с помощью метода обратной итерации на примере %трехдиагональной матрицы %очищаем рабочее пространство clear all

%определяем максимальный порядок матрицы A=Q птах =2 0 0;

%задаем параметр матрицы A=Q

%организуем цикл расчетов собственных векторов %для матриц различных порядков (от 1 до П та X) for n = 1: птах

“/сформируем трехдиагональную матрицу %A=Q порядка П A=zeros( п) ; for i =1: п

A( i , i — 1) =- q; end

A( i , i +1) =- q; end

%цикл расчета собственных векторов методом %обратной итерации for к =1: п

“/сопределяем собственное значение

%возмущаем собственное значение

I a mb d а ( к) =1 a mb d а ( к) +1е — 5 * г a n d п;

“/сформируем правую часть системы уравнений “/сметода обратной итерации b=randn(n, 1);

“/сорганизуется итерационный процесс метода “/собратной итерации с тремя итерациями

“/орешаем систему обратной итерации х 1 =( А-1 a mbdа (к) * еуе( п)) хО; х 0 =х 1/ no г т( х 1); end

“/сформируется матрица, в которой столбцами “/оявляются собственные векторы матрицы A=Q for j = 1: п

еv(j , k) =х 0(j ); end end

“/ооценивается точность найденных собственных “/свекторов для каждого порядка матрицы

error!п)=0; for к =1: п

norm! ( А-1 arnbda! к)*еуе( n) )*ev( : , к) ); end end

%рисуется зависимость погрешности вычисления %собственных векторов от порядка матрицы

р I о t ( 1: nmax, error);

На рис. 6.5 приведена зависимость итоговой ошибки численной оценки собственных векторов методом обратной итерации от порядка матрицы.

Ошибка оценивалась по формуле . Анализ графика

показывает, что ошибка вполне удовлетворительна вплоть до порядка матрицы п = 200.

Рис. 6.5. Зависимость численной оценки собственных векторов от порядка матрицы

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Метод обратной итерации

Метод обратной итерации, по существу, является степенным методом, примененным к соответствующей обратной матрице. Рассмотрим кратко теоретические основы этого метода. Умножая выражение (4.1) на матрицу А -1 , задачу на собственное значение можно записать в другом виде:

Это значит, что собственный вектор матрицы А является собственным вектором матрицы А 1 и ^„(А 1 ) = 1/А,_и(А). Выберем некоторый начальный вектор х (0) и разложим его по собственным векторам матрицы А:

Умножая вектор х (0) k раз на матрицу А -1 , получим

Когда k — [1] [2] — оо_т у(*) стремится к вектору, коллинеарному с вектором Zj. Поэтому последовательные степени матрицы А -1 дают информацию о наименьшем по модулю собственном значении матрицы А. На практике вычислять матрицу А 1 нецелесообразно, так как решение системы Ау = х относительно вектора у требует меньше затрат, чем вычисление у = А *х. Суммируя все эти замечания, можно предложить следующую реализацию метода обратной итерации:

• 1) задать начальный вектор х (0) ;
• 2) для каждого значения k = 0, 1, . решить систему линейных уравнений Ау^ +1) = х ( ^;
• 3) следующее приближение вычисляется как х (Ь1) =

и справедлива следующая оценка

Таким образом, скорость сходимости метода обратной итерации зависит от того, насколько Х меньше, чем |А,₂|.

Пример 4.3 (метод обратной итерации)

Рассмотрим матрицу из примера 4.2. Выберем начальный вектор х (0) = (1, О, О, 0) г и е_р= 10 5 . Результаты вычислений приведены в табл. 4.2.

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

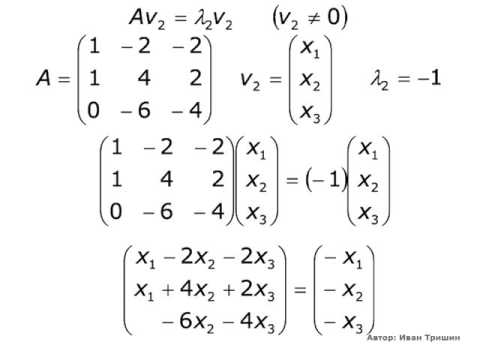
Методы решения задач о собственных
значениях и векторах матриц

Видео:Собственные векторы и собственные значения матрицыСкачать

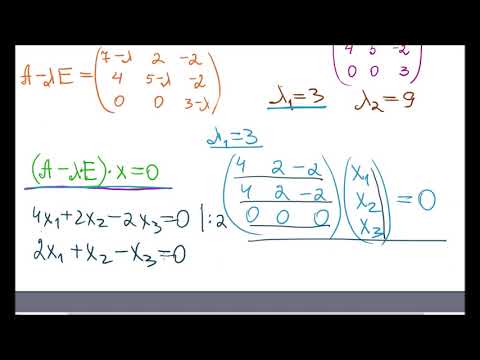
Постановка задачи

Пусть [math]A[/math] — действительная числовая квадратная матрица размера [math](ntimes n)[/math] . Ненулевой вектор [math]X= bigl(x_1,ldots,x_nbigr)^T[/math] размера [math](ntimes1)[/math] , удовлетворяющий условию

называется собственным вектором матрицы [math]A[/math] . Число [math]lambda[/math] в равенстве (2.1) называется собственным значением. Говорят, что собственный вектор [math]X[/math] соответствует (принадлежит) собственному значению [math]lambda[/math] .

Равенство (2.1) равносильно однородной относительно [math]X[/math] системе:

Система (2.2) имеет ненулевое решение для вектора [math]X[/math] (при известном [math]lambda[/math] ) при условии [math]|A-lambda E|=0[/math] . Это равенство есть характеристическое уравнение:

где [math]P_n(lambda)[/math] — характеристический многочлен n-й степени. Корни [math]lambda_1, lambda_2,ldots,lambda_n[/math] характеристического уравнения (2.3) являются собственными (характеристическими) значениями матрицы [math]A[/math] , а соответствующие каждому собственному значению [math]lambda_i,

i=1,ldots,n[/math] , ненулевые векторы [math]X^i[/math] , удовлетворяющие системе

являются собственными векторами.

Требуется найти собственные значения и собственные векторы заданной матрицы. Поставленная задача часто именуется второй задачей линейной алгебры.

Проблема собственных значений (частот) возникает при анализе поведения мостов, зданий, летательных аппаратов и других конструкций, характеризующихся малыми смещениями от положения равновесия, а также при анализе устойчивости численных схем. Характеристическое уравнение вместе с его собственными значениями и собственными векторами является основным в теории механических или электрических колебаний на макроскопическом или микроскопическом
уровнях.

Различают полную и частичную проблему собственных значений, когда необходимо найти весь спектр (все собственные значения) и собственные векторы либо часть спектра, например: [math]rho(A)= max_|lambda_i(A)|[/math] и [math]min_|lambda_i(A)|[/math] . Величина [math]rho(A)[/math] называется спектральным радиусом .

1. Если для собственного значения [math]lambda_i[/math] — найден собственный вектор [math]X^i[/math] , то вектор [math]mu X^i[/math] , где [math]mu[/math] — произвольное число, также является собственным вектором, соответствующим этому же собственному значению [math]lambda_i[/math] .

2. Попарно различным собственным значениям соответствуют линейно независимые собственные векторы; k-кратному корню характеристического уравнения соответствует не более [math]k[/math] линейно независимых собственных векторов.

3. Симметрическая матрица имеет полный спектр [math]lambda_i,

i=overline[/math] , действительных собственных значений; k-кратному корню характеристического уравнения симметрической матрицы соответствует ровно [math]k[/math] линейно независимых собственных векторов.

4. Положительно определенная симметрическая матрица имеет полный спектр действительных положительных собственных значений.

Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать

Метод непосредственного развертывания

Полную проблему собственных значений для матриц невысокого порядка [math](nleqslant10)[/math] можно решить методом непосредственного развертывания. В этом случае будем иметь

Уравнение [math]P_n(lambda)=0[/math] является нелинейным (методы его решения изложены в следующем разделе). Его решение дает [math]n[/math] , вообще говоря, комплексных собственных значений [math]lambda_1,lambda_2,ldots,lambda_n[/math] , при которых [math]P_n(lambda_i)=0

(i=overline)[/math] . Для каждого [math]lambda_i[/math] может быть найдено решение однородной системы [math](A-lambda_iE)X^i=0,

i=overline[/math] . Эти решения [math]X^i[/math] , определенные с точностью до произвольной константы, образуют систему [math]n[/math] , вообще говоря, различных векторов n-мерного пространства. В некоторых задачах несколько этих векторов (или все) могут совпадать.

Видео:А.7.40 Метод Якоби поиска собственных векторов и значений симметричных матрицСкачать

Алгоритм метода непосредственного развертывания

1. Для заданной матрицы [math]A[/math] составить характеристическое уравнение (2.5): [math]|A-lambda E|=0[/math] . Для развертывания детерминанта [math]|A-lambda E|[/math] можно использовать различные методы, например метод Крылова, метод Данилевского или другие методы.

2. Решить характеристическое уравнение и найти собственные значения [math]lambda_1, lambda_2, ldots,lambda_n[/math] . Для этого можно применить методы, изложенные далее.

3. Для каждого собственного значения составить систему (2.4):

и найти собственные векторы [math]X^i[/math] .

Замечание. Каждому собственному значению соответствует один или несколько векторов. Поскольку определитель [math]|A-lambda_iE|[/math] системы равен нулю, то ранг матрицы системы меньше числа неизвестных: [math]operatorname(A-lambda_iE)=r и в системе имеется ровно [math]r[/math] независимых уравнений, а [math](n-r)[/math] уравнений являются зависимыми. Для нахождения решения системы следует выбрать [math]r[/math] уравнений с [math]r[/math] неизвестными так, чтобы определитель составленной системы был отличен от нуля. Остальные [math](n-r)[/math] неизвестных следует перенести в правую часть и считать параметрами. Придавая параметрам различные значения, можно получить различные решения системы. Для простоты, как правило, попеременно полагают значение одного параметра равным 1, а остальные равными 0.

Пример 2.1. Найти собственные значения и собственные векторы матрицы [math]Ain mathbb^[/math] , где [math]A=begin3&-2\-4&1end[/math] .

1. Запишем уравнение (2.5): [math]|A-lambda E|= begin3-lambda&-2\-4& 1-lambda end= lambda^2-4 lambda-5=0[/math] , отсюда получаем характеристическое уравнение [math]P_2(lambda)equiv lambda^2-4 lambda-5=0[/math] .

2. Находим его корни (собственные значения): [math]lambda_1=5,

3. Составим систему [math](A-lambda_iE)X^i=0,

i=1,2[/math] , для каждого собственного
значения и найдем собственные векторы:

Отсюда [math]x_1^1=-x_2^1[/math] . Если [math]x_2^1=mu[/math] , то [math]x_1^1=-mu[/math] . В результате получаем [math]X^1= bigl^T= bigl^T[/math] .

Для [math]lambda_2=-1[/math] имеем

Отсюда [math]x_2^2=2x_1^2[/math] . Если [math]x_1^2=mu[/math] , то [math]x_2^2=2mu[/math] . В результате получаем [math]X^2= bigl^T= bigl^T[/math] , где [math]mu[/math] — произвольное действительное число.

Пример 2.2. Найти собственные значения и собственные векторы матрицы [math]A= begin2&-1&1\-1&2&-1\0&0&1end[/math] .

1. Запишем характеристическое уравнение (2.5):

2. Корни характеристического уравнения: [math]lambda_=1[/math] (кратный корень), [math]lambda_3=3[/math] — собственные значения матрицы.

3. Найдем собственные векторы.

Для [math]lambda_=1[/math] запишем систему [math](A-lambda_E)cdot X^=0colon[/math]

Поскольку [math]operatorname(A-lambda_E)=1[/math] , в системе имеется одно независимое уравнение

x_3^=3[/math] , получаем [math]x_1^=1[/math] и собственный вектор [math]X^1= begin1&1&0end^T[/math] .

x_3^=1[/math] , получаем [math]x_1^=-1[/math] и другой собственный вектор [math]X^2= begin-1&0&1end^T[/math] . Заметим, что оба собственных вектора линейно независимы.

Для собственного значения [math]lambda_3=3[/math] запишем систему [math](A-lambda_3E)cdot X^3=0colon[/math]

Поскольку [math]operatorname(A-lambda_3E)=2[/math] , то выбираем два уравнения:

x_1^3=-x_2^3[/math] . Полагая [math]x_2^3=1[/math] , получаем [math]x_1^3=-1[/math] и собственный вектор [math]X^3=begin-1&1&0 end^T[/math] .

Видео:Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать

Метод итераций для нахождения собственных значений и векторов

Для решения частичной проблемы собственных значений и собственных векторов в практических расчетах часто используется метод итераций (степенной метод). На его основе можно определить приближенно собственные значения матрицы [math]A[/math] и спектральный радиус [math]rho(A)= max_bigl|lambda_i(A)bigr|[/math] .

Пусть матрица [math]A[/math] имеет [math]n[/math] линейно независимых собственных векторов [math]X^i,

i=1,ldots,n[/math] , и собственные значения матрицы [math]A[/math] таковы, что

Видео:Собственные векторы и собственные значенияСкачать

Алгоритм метода итераций

1. Выбрать произвольное начальное (нулевое) приближение собственного вектора [math]X^[/math] (второй индекс в скобках здесь и ниже указывает номер приближения, а первый индекс без скобок соответствует номеру собственного значения). Положить [math]k=0[/math] .

lambda_1^= frac<x_i^><x_i^>[/math] , где [math]i[/math] — любой номер [math]1leqslant ileqslant n[/math] , и положить [math]k=1[/math] .

4. Найти [math]lambda_1^= frac<x_i^><x_i^>[/math] , где [math]x_i^, x_i^[/math] — соответствующие координаты векторов [math]X^[/math] и [math]X^[/math] . При этом может быть использована любая координата с номером [math]i,

1leqslant ileqslant n[/math] .

5. Если [math]Delta= bigl|lambda_1^- lambda_1^bigr|leqslant varepsilon[/math] , процесс завершить и положить [math]lambda_1cong lambda_1^[/math] . Если varepsilon»>[math]Delta>varepsilon[/math] , положить [math]k=k+1[/math] и перейти к пункту 3.

1. Процесс последовательных приближений

сходится, т.е. при [math]xtoinfty[/math] вектор [math]X^[/math] стремится к собственному вектору [math]X^1[/math] . Действительно, разложим [math]X^[/math] по всем собственным векторам: [math]textstyle<X^= sumlimits_^ c_iX^i>[/math] . Так как, согласно (2.4), [math]AX^i= lambda_iX^i[/math] , то

При большом [math]k[/math] дроби [math]<left(fracright)!>^k, ldots, <left(fracright)!>^k[/math] малы и поэтому [math]A^kX^= c_1lambda_1^kX^1[/math] , то есть [math]X^to X^1[/math] при [math]ktoinfty[/math] . Одновременно [math]lambda_1= limlimits_ frac<x_^><x_^>[/math] .

2. Вместо применяемой в пункте 4 алгоритма формулы для [math]lambda_1^[/math] можно взять среднее арифметическое соответствующих отношений для разных координат.

3. Метод может использоваться и в случае, если наибольшее по модулю собственное значение матрицы [math]A[/math] является кратным, т.е.

4. При неудачном выборе начального приближения [math]X^[/math] предел отношения [math]frac<x_i^><x_i^>[/math] может не существовать. В этом случае следует задать другое начальное приближение.

5. Рассмотренный итерационный процесс для [math]lambda_1[/math] сходится линейно, с параметром [math]c=frac[/math] и может быть очень медленным. Для его ускорения используется алгоритм Эйткена.

6. Если [math]A=A^T[/math] (матрица [math]A[/math] симметрическая), то сходимость процесса при определении [math]rho(A)[/math] может быть ускорена.

7. Используя [math]lambda_1[/math] , можно определить следующее значение [math]lambda_2[/math] по формуле [math]lambda_2= frac<x_i^- lambda_1 x_i^><x_i^- lambda_1 x_i^>

(i=1,2,ldots,n)[/math] . Эта формула дает грубые значения для [math]lambda_2[/math] , так как значение [math]lambda_1[/math] является приближенным. Если модули всех собственных значений различны, то на основе последней формулы можно вычислять и остальные [math]lambda_j

8. После проведения нескольких итераций рекомендуется «гасить» растущие компоненты получающегося собственного вектора. Это осуществляется нормировкой вектора, например, по формуле [math]frac<X^><|X^|_1>[/math] .

Пример 2.3. Для матрицы [math]A=begin5&1&2\ 1&4&1\ 2&1&3 end[/math] найти спектральный радиус степенным методом с точностью [math]varepsilon=0,,1[/math] .

1. Выбирается начальное приближение собственного вектора [math]X^= begin 1&1&1 end^T[/math] . Положим [math]k=0[/math] .

5. Так как varepsilon»>[math]bigl|lambda_1^- lambda_1^bigr|= 0,!75> varepsilon[/math] , то процесс необходимо продолжить. Результаты вычислений удобно представить в виде табл. 10.10.

Точность по достигнута на четвертой итерации. Таким образом, в качестве приближенного значения [math]lambda_1[/math] берется 6,9559, а в качестве собственного вектора принимается [math]X^1= begin 2838& 1682& 1888end^T[/math] .

Так как собственный вектор определяется с точностью до постоянного множителя, то [math]X^1[/math] лучше пронормировать, т.е. поделить все его компоненты на величину нормы. Для рассматриваемого примера получим

Согласно замечаниям, в качестве собственного значения [math]lambda_1[/math] матрицы можно взять не только отношение

а также их среднее арифметическое [math]fracapprox 6,!8581[/math] .

Пример 2.4. Найти максимальное по модулю собственное значение матрицы [math]A=begin2&-1&1\ -1&2&-1\ 0&0&3 end[/math] и соответствующий собственный вектор.

1. Зададим начальное приближение [math]X^= begin1&-1&1 end^T[/math] и [math]varepsilon=0,!0001[/math] .

Выполним расчеты согласно методике (табл. 10.11).

В результате получено собственное значение [math]lambda_1cong 3,!00003[/math] и собственный вектор [math]X^1= begin 88573&-88573&1end^T[/math] или после нормировки

Видео:Собственные значения и собственные векторыСкачать

Метод вращений для нахождения собственных значений

Метод используется для решения полной проблемы собственных значений симметрической матрицы и основан на преобразовании подобия исходной матрицы [math]Ainmathbb^[/math] с помощью ортогональной матрицы [math]H[/math] .

Напомним, что две матрицы [math]A[/math] и [math]A^[/math] называются подобными ( [math]Asim A^[/math] или [math]A^sim A[/math] ), если [math]A^=H^AH[/math] или [math]A=HA^H^[/math] , где [math]H[/math] — невырожденная матрица.

В методе вращений в качестве [math]H[/math] берется ортогональная матрица, такая, что [math]HH^=H^H=E[/math] , т.е. [math]H^=H^[/math] . В силу свойства ортогонального преобразования евклидова норма исходной матрицы [math]A[/math] не меняется. Для преобразованной матрицы [math]A^[/math] сохраняется ее след и собственные значения [math]lambda_icolon[/math]

[math]operatorname

A= sum_^a_= sum_^ lambda_i(A)= operatorname

A^.[/math]

При реализации метода вращений преобразование подобия применяется к исходной матрице [math]A[/math] многократно:

Формула (2.6) определяет итерационный процесс, где начальное приближение [math]A^=A[/math] . На k-й итерации для некоторого выбираемого при решении задачи недиагонального элемента [math]a_^,

ine j[/math] , определяется ортогональная матрица [math]H^[/math] , приводящая этот элемент [math]a_^[/math] (а также и [math]a_^[/math] ) к нулю. При этом на каждой итерации в качестве [math]a_^[/math] выбирается наибольший по модулю. Матрица [math]H^[/math] называемая матрицей вращения Якоби, зависит от угла [math]varphi^[/math] и имеет вид

В данной ортогональной матрице элементы на главной диагонали единичные, кроме [math]h_^= cosvarphi^[/math] и [math]h_^=cosvarphi^[/math] , а остальные элементы нулевые, за исключением [math]h_^=-sinvarphi^[/math] , [math]h_^=sinvarphi^[/math] ( [math]h_[/math] -элементы матрицы [math]H[/math] ).

Угол поворота [math]varphi^[/math] определяется по формуле

где [math]|2varphi^|leqslant frac,

i ( [math]a_[/math] выбирается в верхней треугольной наддиагональной части матрицы [math]A[/math] ).

В процессе итераций сумма квадратов всех недиагональных элементов [math]sigms(A^)[/math] при возрастании [math]k[/math] уменьшается, так что [math]sigms(A^) . Однако элементы [math]a_^[/math] приведенные к нулю на k-й итерации, на последующей итерации немного возрастают. При [math]ktoinfty[/math] получается монотонно убывающая ограниченная снизу нулем последовательность sigma(A^)> ldots> sigma(A^)>ldots»>[math]sigma(A^)> sigma(A^)> ldots> sigma(A^)>ldots[/math] . Поэтому [math]sigma(A^)to0[/math] при [math]ktoinfty[/math] . Это и означает сходимость метода. При этом [math]A^to Lambda= operatorname(lambda_1,ldots,lambda_n)[/math] .

Замечание. В двумерном пространстве с введенной в нем системой координат [math]Oxy[/math] с ортонормированным базисом [math]<vec,vec>[/math] матрица вращения легко получается из рис. 2.1, где система координат [math]Ox’y'[/math] повернута на угол [math]varphicolon[/math]

Таким образом, для компонент [math]vec,’,, vec,'[/math] будем иметь [math]bigl(vec,’,vec,’bigr)= bigl(vec,vecbigr)cdot! begin cos varphi&-sin varphi\ sin varphi& cos varphiend[/math] . Отсюда следует, что в двумерном пространстве матрица вращения имеет вид [math]H= begin cos varphi&-sin varphi\ sin varphi& cos varphiend[/math] . Отметим, что при [math]n=2[/math] для решения задачи требуется одна итерация.

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Алгоритм метода вращений

1. Положить [math]k=0,

A^=A[/math] и задать 0″>[math]varepsilon>0[/math] .

2. Выделить в верхней треугольной наддиагональной части матрицы [math]A^[/math] максимальный по модулю элемент [math]a_^,

Если [math]|a_^|leqslant varepsilon[/math] для всех [math]ine j[/math] , процесс завершить. Собственные значения определяются по формуле [math]lambda_i(A^)=a_^,

Собственные векторы [math]X^i[/math] находятся как i-e столбцы матрицы, получающейся в результате перемножения:

Если varepsilon»>[math]bigl|a_^bigr|>varepsilon[/math] , процесс продолжается.

3. Найти угол поворота по формуле [math]varphi^= frac operatorname frac<2a_^><a_^-a_^>[/math] .

4. Составить матрицу вращения [math]H^[/math] .

5. Вычислить очередное приближение [math]A^= bigl(H^bigr)^T A^ H^[/math] .Положить [math]k=k+1[/math] и перейти к пункту 2.

1. Используя обозначение [math]overline

_k= frac<2a_^><a_^-a_^>[/math] , можно в пункте 3 алгоритма вычислять элементы матрицы вращения по формулам

2. Контроль правильности выполнения действий по каждому повороту осуществляется путем проверки сохранения следа преобразуемой матрицы.

3. При [math]n=2[/math] для решения задачи требуется одна итерация.

Пример 2.5. Для матрицы [math]A=begin 2&1\1&3 end[/math] методом вращений найти собственные значения и собственные векторы.

1. Положим [math]k=0,

2°. Выше главной диагонали имеется только один элемент [math]a_=a_=1[/math] .

3°. Находим угол поворота матрицы по формуле (2.7), используя в расчетах 11 цифр после запятой в соответствии с заданной точностью:

4°. Сформируем матрицу вращения:

5°. Выполним первую итерацию:

Очевидно, след матрицы с заданной точностью сохраняется, т.е. [math]sum_^a_^= sum_^a_^=5[/math] . Положим [math]k=1[/math] и перейдем к пункту 2.

2. Максимальный по модулю наддиагональный элемент [math]|a_|= 4,!04620781325cdot10^ . Для решения задачи (подчеркнем, что [math]n=2[/math] ) с принятой точностью потребовалась одна итерация, полученную матрицу можно считать диагональной. Найдены следующие собственные значения и собственные векторы:

Пример 2.6. Найти собственные значения и собственные векторы матрицы [math]A=begin5&1&2\ 1&4&1\ 2&1&3 end[/math] .

1. Положим [math]k=0,

2°. Выделим максимальный по модулю элемент в наддиагональнои части: [math]a_^=2[/math] . Так как varepsilon=0,!001″>[math]a_=2> varepsilon=0,!001[/math] , то процесс продолжается.

3°. Находим угол поворота:

4°. Сформируем матрицу вращения: [math]H^= begin0,!85065&0&-0,!52573\ 0&1&0\ 0,!52573&0&0,!85065 end[/math] .

5°. Выполним первую итерацию: [math]A^= bigl(H^bigr)^T A^H^= begin 6,!236&1,!376&2,!33cdot10^\ 1,!376&4&0,!325\ 2,!33cdot10^&0,!325&1,!764 end[/math] . Положим [math]k=1[/math] и перейдем к пункту 2.

2(1). Максимальный по модулю наддиагональный элемент [math]a_^=1,!376[/math] . Так как varepsilon=0,!001″>[math]a_^> varepsilon=0,!001[/math] , процесс продолжается.

3(1). Найдем угол поворота:

4(1). Сформируем матрицу вращения: [math]H^= begin 0,!902937&-0,!429770&0\ 0,!429770&0,!902937&0\ 0&0&1 end[/math] .

5(1). Выполним вторую итерацию: [math]A^= bigl(H^bigr)^T A^H^= begin 6,!891& 2,!238cdot10^&0,!14\ 2,!238cdot10^& 3,!345&0,!293\ 0,!14&0,!293&1,!764 end[/math] . Положим [math]k=2[/math] и перейдем к пункту 2.

2(2). Максимальный по модулю наддиагональный элемент varepsilon=0,!001″>[math]a_^=0,!293> varepsilon=0,!001[/math] .

3(2). Найдем угол поворота:

4(2). Сформируем матрицу вращения [math]H^= begin1&0&0\ 0&0,!9842924& -0,!1765460\ 0& 0,!1765460& 0,!9842924end[/math] .

5(2). Выполним третью итерацию и положим [math]k=3[/math] и перейдем к пункту 2:

2(3). Максимальный по модулю наддиагональный элемент varepsilon»>[math]a_^= 0,!138>varepsilon[/math] .

3(3). Найдем угол поворота:

4(3). Сформируем матрицу вращения: [math]H^= begin 0,!999646&0&-0,!026611\ 0&1&0\ 0,!026611&0&0,!999646 end[/math] .

5(3). Выполним четвертую итерацию и положим [math]k=4[/math] и перейдем к пункту 2:

2(4). Так как varepsilon»>[math]a_^=0,!025>varepsilon[/math] , процесс повторяется

3(4). Найдем угол поворота

4(4). Сформируем матрицу вращения: [math]H^= begin 0,!9999744&-0,!0071483&0\ 0,!0071483&0,!9999744&0\ 0&0&1 end[/math] .

5(4). Выполним пятую итерацию и положим [math]k=5[/math] и перейдем к пункту 2:

2(5). Так как наибольший по модулю наддиагональный элемент удовлетворяет условию [math]bigl|-6,!649cdot10^bigr| , процесс завершается.

Собственные значения: [math]lambda_1cong a_^= 6,!895,,

lambda_3cong a_^=1,!707,,[/math] . Для нахождения собственных векторов вычислим

X^3=begin-0,!473\-0,!171\0,!864 end[/math] или после нормировки

🎦 Видео

Диагонализация матрицы линейного оператора. ТемаСкачать

Метод простой итерации Пример РешенияСкачать

Айгенвектора и айгензначения | Сущность Линейной Алгебры, глава 10Скачать

Занятие 13 (2023-24): Типовая структура верификационного ООП-окруженияСкачать

Вычислительные методы алгебры - Степенной метод, метод вращенийСкачать

Ядро и образ линейного оператора. ТемаСкачать

Овчинников А. В. - Линейная алгебра - Собственные значения и собственные векторы линейного оператораСкачать

А.7.39 Вычисление собственных значений и собственных векторовСкачать

Собственные значения и собственные векторы. ПримерСкачать

Численные методы. Лекция 11Скачать

7 4 Собственные векторы и собственные значенияСкачать