Сколько диагоналей можно провести из одной вершины четырехугольника

Вопросы к параграфу

1. Какая фигура ограничивает многоугольник? — Замкнутая ломаная, звенья которой не пересекаются.

2. Могут ли звенья ломаной, ограничивающей многоугольник, пересекаться? — Нет, не могут.

3. Какие элементы многоугольника вы знаете? — Вершина, сторона, углы многоугольника.

4. Как называют и обозначают многоугольник? — Многоугольники называют и обозначают по его вершинам. Чтобы записать название многоугольника, надо последовательно записать все его вершины.

5. Что называют периметром многоугольника? — Периметр многоугольника — это сумма длин все его сторон.

6. Какие многоугольники называют равными? — Многоугольники называют равными, если они совпадают при наложении.

7. Какие фигуры называют равными? — Фигуры называют равными, если они совпадают при наложении.

Решаем устно

1. Сумму чисел 24 и 18 уменьшите на 33.

(24 + 18) — 33 = 42 — 33 = 9

2. Разность чисел 30 и 14 увеличьте в 3 раза.

(30 — 14) • 3 = 16 • 48

3. Произведение чисел 12 и 5 увеличьте на 19.

(12 • 5) + 19 = 60 + 19 = 79

4. Частное чисел 189 и 9 уменьшите в 7 раз.

(189 : 9) : 7 = 21 : 7 = 3

5. Укажите среди данных отрезков равные, если:

• АВ = 5 см 3 мм = 53 мм = TQ
• CD = 4 м 5 см = 405 см
• РК = 45 см
• EF = 2 дм 8 мм = 20 см 8 мм = 208 мм = MN
• TQ = 53 мм = 5 см 3 мм = АВ
• MN= 208 мм = 20 см 8 мм = 2 дм 8 мм = EF

Ответ: АВ = TQ и EF = MN.

Упражнения

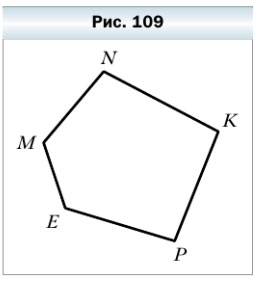
321. Назовите вершины и стороны пятиугольника, изображённого на рисунке 109.

• Вершины пятиугольника: N, K, P, E, M
• Стороны пятиугольника: NK, KP, PE, EM, EN.

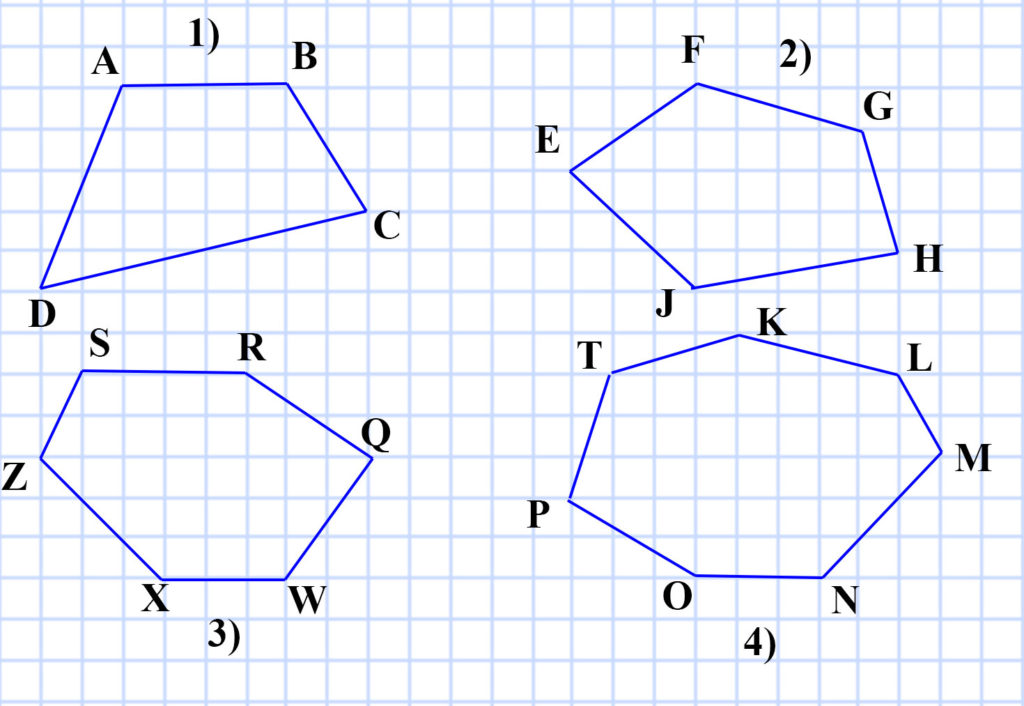
322. Начертите: 1) четырёхугольник; 2) пятиугольник; 3) шестиугольник; 4) семиугольник .

1. Четырехугольник ABCD
2. Пятиугольник EFGHJ
3. Шестиугольник SRQWXZ
4. семиугольник TKLMNOP

323. Вычислите периметр пятиугольника, стороны которого равны 2 см, 4 см, 5 см 5 мм, 6 см, 7 см.

Периметр многоугольника равен сумме длин его сторон.

2 см + 4 см + 5 см 5 мм + 6 см + 7 см = 24 см 5 мм — периметр данного пятиугольника.

Ответ: 24 см 5 мм.

324. Вычислите периметр шестиугольника, три стороны которого равны по 8 см, а три другие — по 10 см.

Периметр многоугольника равен сумме длин его сторон.

8 • 3 + 10 • 3 = 24 + 30 = 54 (см) — периметр данного шестиугольника.

325. Нарисуйте в тетради фигуру, равную той, которая изображена на рисунке 110.

326. Нарисуйте в тетради фигуру, равную той, которая изображена на рисунке 111.

327. Одна из сторон четырёхугольника равна 8 см, вторая сторона в 3 раза больше первой, а третья — на 7 см меньше второй и на 9 см больше четвёртой. Вычислите периметр четырёхугольника.

1) 8 • 3 = 24 (см) — длина второй стороны четырёхугольника.

2) 24 — 7 = 17 (см) — длина третьей стороны четырёхугольника.

3) 17 — 9 = 8 (см) — длина четвёртой стороны четырёхугольника.

4) 8 + 24 + 17 + 8 = 57 (см) — периметр четырёхугольника.

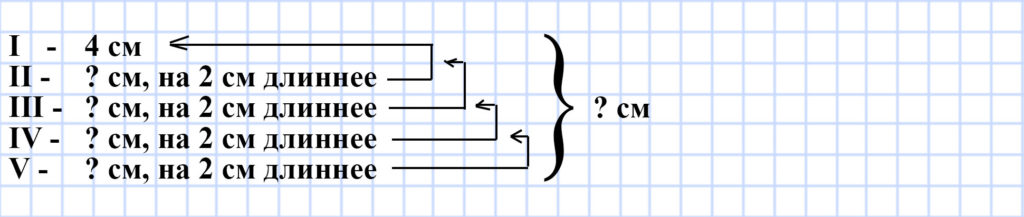
328. Стороны пятиугольника пронумеровали. Первая сторона равна 4 см, а каждая следующая сторона на 2 см длиннее предыдущей. Вычислите периметр пятиугольника.

1) 4 + 2 = 6 (см) — длина второй стороны пятиугольника.

2) 6 + 2 = 8 (см) — длина третьей стороны пятиугольника.

3) 8 + 2 = 10 (см) — длина четвёртой стороны пятиугольника.

4) 10 + 2 = 12 (см) — длина пятой стороны пятиугольника.

5) 4 + 6 + 8 + 10 + 12 = 40 (см) — периметр пятиугольника.

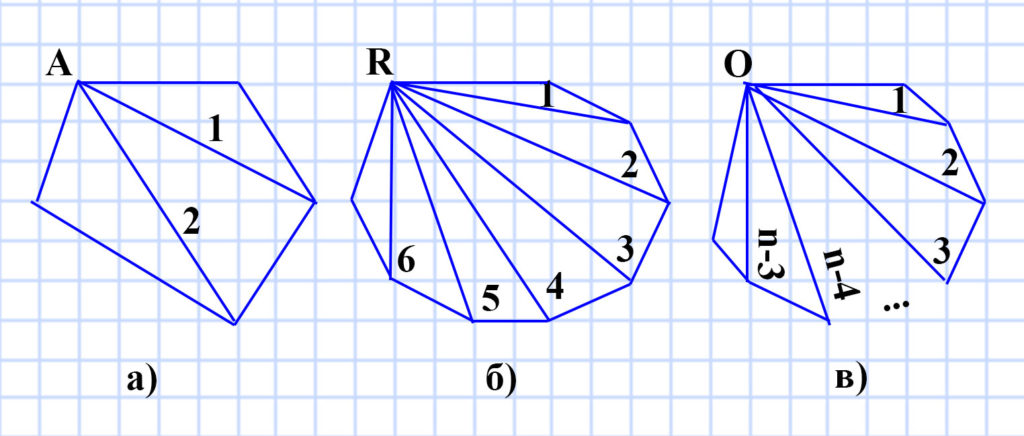
329. 1) Сколько диагоналей можно провести из одной вершины: а) пятиугольника; б) девятиугольника; в) и-угольника, где п > 3?

а) Из одной вершины пятиугольника можно провести 2 диагонали.

б) Из одной вершины девятиугольника можно провести 6 диагоналей.

в) Из одной вершины n-угольника можно провести (n-3) диагоналей, так как:

• первая вершина является исходной;
• диагональ ко второй вершине совпадает со одной из сторон, прилегающей к исходной вершине;
• диагональ к последней вершине совпадает с другой из сторон, прилегающей к исходной вершине.

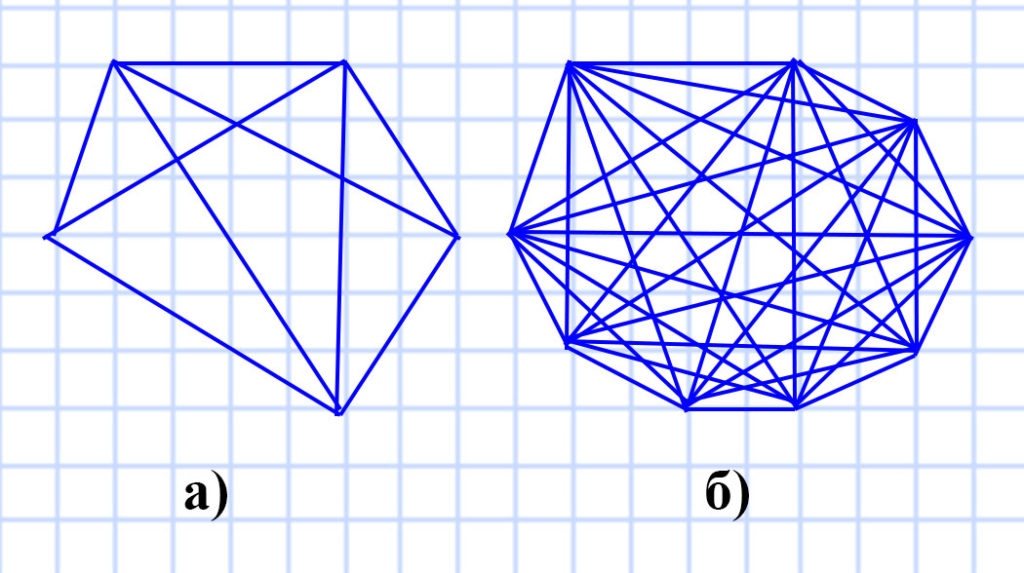
2) Сколько всего диагоналей можно провести: а) в пятиугольнике; б) в девятиугольнике; в) в и-угольнике, где п > 3?

а) Мы знаем, что из одной вершины пятиугольника можно провести 2 диагонали (n-3), Значит из 5 вершин можно провести 5 • 2 = 10 диагоналей (n • (n-3)). Но если провести все 10 диагоналей, то каждая пара из них будет совпадать, так как одна диагональ всегда соединяет две вершины. Значит всего в пятиугольнике можно провести 10 : 2 = 5 диагоналей ((n •(n-3) : 2). Рисунок подтверждает наш вывод.

б) Мы знаем, что из одной вершины девятиугольника можно провести 6 диагоналей (n-3 = 9 — 3 = 6), Значит из 9 вершин можно провести 9 • 6 = 54 диагонали (n • (n-3) = 9 • (9 — 3) = 9 • 6 = 54). Но если провести все 54 диагонали, то каждая пара из них будет совпадать, так как одна диагональ всегда соединяет две вершины. Значит всего в девятиугольнике можно провести 54 : 2 = 27 диагоналей ((n • (n-3) : 2 = 9 • (9 — 3) : 2 = 9 • 6 : 2 = 54 : 2 = 27). Рисунок подтверждает наш вывод.

в) Исследуя предыдущие два задания мы вывели формулу, по которой можно посчитать количество возможных диагоналей в n-угольнике, при n > 3: n • (n-3) : 2. Это значит, у количество диагоналей:

• у четырёхугольника — n • (n-3) : 2 = 4 • (4 — 3) : 2 = 4 • 1 : 2 = 4 : 2 = 2 — верно
• у шестиугольника — n • (n-3) : 2 = 6 • (6 — 3) : 2 = 6 • 3 : 2 = 18 : 2 = 9 — верно
• у семиугольника — n • (n-3) : 2 = 7 • (7 — 3) : 2 = 7 • 4 : 2 = 1=28 : 2 = 14 — верно
• и т.д.

Ответ: 5, 27, n • (n-3) : 2.

330. Как, используя шаблон угла, градусная мера которого 13°, построить угол, градусная мера которого равна 2°?

Для того, чтобы используя шаблон угла, градусная мера которого 13°, построить угол, градусная мера которого равна 2° надо:

1. прочертить прямую линию и отметить на ней точку вершины развёрнутого угла;
2. начиная от одного из лучей развёрнутого угла последовательно 14 раз отложить по шаблону угол в 13°;
3. так как 13° • 14 = 182°, то последний из отложенных по шаблону углов будет на 2° выходить за границы развёрнутого угла;
4. угол, выходящий за границы развёрнутого угла, как раз и будет искомым углом с градусной мерой 2°.

331. Как построить угол, градусная мера которого 1°, используя шаблон угла, градусная мера которого равна:

а) 19°

Для того, чтобы используя шаблон угла, градусная мера которого 19°, построить угол, градусная мера которого равна 1° надо:

1. прочертить прямую линию и отметить на ней точку вершины развёрнутого угла;
2. начиная от одного из лучей развёрнутого угла последовательно 19 раз отложить по шаблону угол в 19°;
3. так как 19° • 19 = 361°, то последний из отложенных по шаблону углов будет на 1° выходить за границы двух развёрнутых углов;
4. угол, выходящий за границы развёрнутых углов, как раз и будет искомым углом с градусной мерой 1°.

б) 7°

Для того, чтобы используя шаблон угла, градусная мера которого 7°, построить угол, градусная мера которого равна 1° надо:

1. прочертить прямую линию и отметить на ней точку вершины развёрнутого угла.
2. провести из этой точки перпендикуляр к прямой;
3. начиная от одного из лучей развёрнутого угла последовательно 13 раз отложить по шаблону угол в 7°;
4. так как 7° • 13 = 91°, то последний из отложенных по шаблону углов будет на 1° выходить за границы прямого угла образованного перпендикуляром к прямой;
5. угол, выходящий за границы прямого угла, как раз и будет искомым углом с градусной мерой 1°.

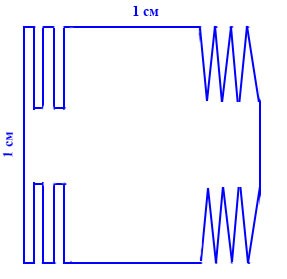
332. Существует ли многоугольник с периметром, равным 1 000 000 см, который можно целиком расположить в квадрате со стороной 1 см?

Да, теоретически такой многоугольник существует. Для этого надо из квадрата со стороной 1 см вырезать множество полосок либо треугольников, либо ещё каких-нибудь фигур вдоль нескольких сторон исходного квадрата. Точное количество таких вырезанных фигур будет зависеть от длины вырезаемых из квадрата сторон фигуры, а также от длины оставшихся от исходного квадрата сторон.

В реальности такую операцию способны выполнить только суперточные приборы, например лазерный принтер. Кроме того, необходимо провести очень точный расчёт вырезаемых фигур.

Упражнения для повторения

333. Сравните:

1) 3 986 г и 4 кг: 4 кг = 4000 г ⇒ 3 986 г

2) 6 м и 712 см: 6 м = 600 см ⇒ 600 см

3) 60 см и 602 мм: 60 см = 600 мм ⇒ 600 мм

4) 999 кг и 10 ц: 10 ц = 1000 кг ⇒ 999 кг

334. Выполните сложение, выбирая удобный порядок вычислений:

1) (636 + 927) + 364 = (636 + 364) + 927 = 1 000 + 927 = 1 927

2) (425 + 798) + 675 = (425 + 675) + 798 = 1 100 + 798 = 1 898

3) 212 + 493 + 788 + 807 = (212 + 788) + (493 + 807) = 1 000 + 1 300 = 2 300

4) 161 + 455 + 839 + 945 = (161 + 839) + (455 + 945) = 1 000 + 1 400 = 2 400

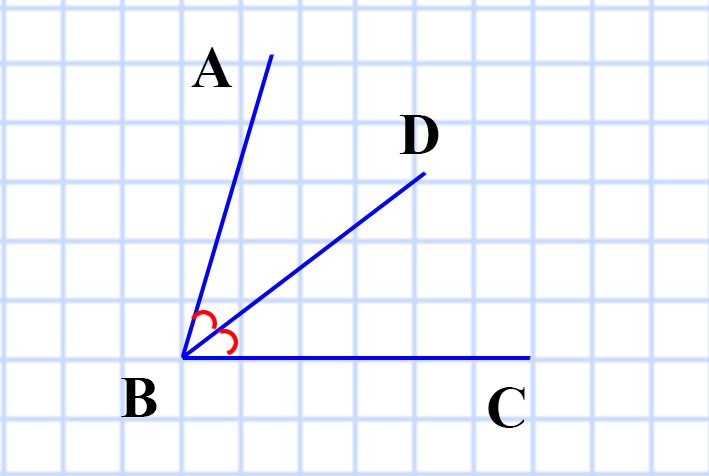
335. Известно, что ∠ABC = 74°, а луч BD — его биссектриса. Вычислите величину угла DBC.

Мы знаем, что биссектриса угла всегда делит угол пополам. Значит:

∠DBC = ∠ABC : 2 = 74° : 2 = 37°

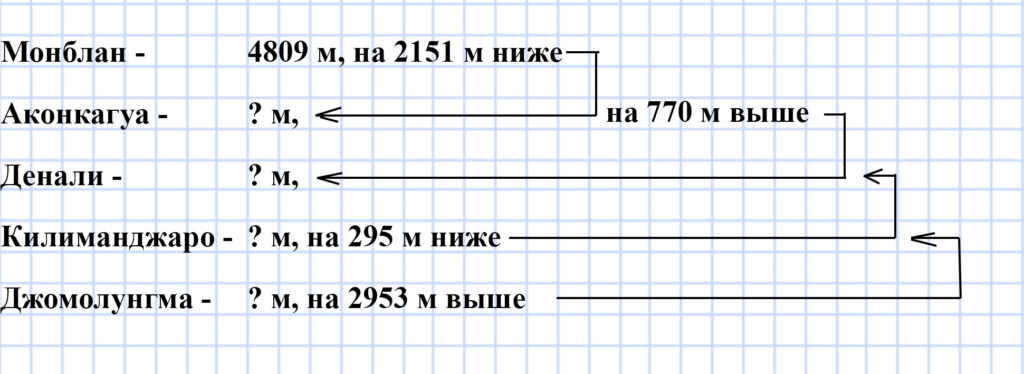
336. Высота самой высокой горы Западной Европы Монблан равна 4 809 м. Она на 2 151 м ниже самой высокой горы Южной Америки Аконкагуа, которая на 770 м выше самой высокой горы Северной Америки Денали. Какова высота самой высокой горы Африки Килиманджаро, если она на 295 м ниже горы Денали? Какова высота самой высокой горы мира Джомолунгмы (Эверест) (рис. 112), если она на 2 953 м выше горы Килиманджаро?

1) 4 809 + 2 151 = 6 960 (м) — высота горы Аконкагуа.

2) 6 960 — 770 = 6 190 (м) — высота горы Денали.

3) 6 190 — 295 = 5 895 (м) — высота горы Килиманджаро.

4) 5 895 + 2 953 = 8 848 (м) — высота горы Джомолунгма.

Ответ: 8 848 метров.

Задача от мудрой совы

337. Лимоны одинаковой массы продают поштучно. Масса каждого лимона составляет целое количество граммов. Купили больше двух, но меньше семи лимонов. Масса всей покупки составляет 850 г. Какова масса одного лимона?

Так как купили больше двух, но меньше семи лимонов, то количество купленных лимонов может быть либо 3, либо 4, либо 5, либо 6.

Масса каждого лимона — целое число, причём все лимоны одинаковые. Проверим, на какое из возможных чисел (3, 4, 5 или 6) общая масса покупки 850 г делится без остатка. Для этого применим метод подбора.

Под заданные условия подходит только число 5.

Видео:Диагональ многоугольникаСкачать

Сколько диагоналей у выпуклого 16 угольника?

Видео:Диагонали в многоугольниках. Есть ли зависимость между количеством вершин и диагоналей в n-угольникеСкачать

Сколько диагоналей имеет 16 угольник?

Ответ: Объяснение: Считаем количество рёбер в полном графе, а затем вычитаем стороны 16-угольника. 16*((16-3))/2 = 104 диагоналей.

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Сколько диагоналей у 7 угольника?

Из каждого угла 7-угольника выходит 4 диагонали и 2 стороны. Получается, что число диагоналей равно 7*4 = 28.

Видео:Диагонали многоугольникаСкачать

Сколько всего диагоналей у 20 угольника?

Значит, из одной вершины этого многоугольника можно провести 9 − 3 = 6 диагоналей.

Видео:Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

Сколько диагоналей имеет правильный 12 угольник?

У него три диагонали, которые попарно перпендикулярно пересекаются в центре.

Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Сколько диагоналей в прямоугольнике?

Диагонали прямоугольников и их свойства

14) называются диагоналями прямоугольника .

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Сколько существует диагоналей у выпуклого пятиугольника?

Ответ: 5 диагоналей.

Видео:Нахождение числа диагоналей выпуклого шестиугольникаСкачать

Сколько диагоналей в выпуклом 13 Угольнике?

Из каждой вершины исходного 13-угольника выходит не более двух диагоналей, которые являются сторонами рассматриваемого многоугольника. Каждой диагонали соответствуют две вершины, поэтому число сторон рассматриваемого многоугольника не превосходит 13.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Сколько диагоналей имеет выпуклый Десятиугольник комбинаторика?

21 отрезок. Из них 7 — это стороны нашего 7-угольника.

Видео:Свойства диагоналей прямоугольника. Свойства диагоналей квадрата | Математика 4 класс #9 | ИнфоурокСкачать

Сколько диагоналей в 9угольнике?

Кроме того, одна диагональ принадлежит одновременно двум вершинам. n * (n-3) / 2 = 9 * (9-3) / 2 = 27 диагоналей.

Видео:8 класс, 4 урок, ПараллелограммСкачать

Сколько диагоналей в четырехугольнике?

У него три диагонали, которые попарно перпендикулярно пересекаются в центре.

Видео:Четырехугольники. Вебинар | МатематикаСкачать

Сколько диагоналей в выпуклом Пятиугольнике Двадцатиугольника?

б) 20 • (20 – 3) : 2 = 20 • 17 : 2 = 170 (диагоналей) – в выпуклом двадцатиугольнике.

Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Сколько диагоналей выходит из одной вершины Девятиугольника?

Значит шесть диагонали у девятиугольника из каждой вершине.

Видео:Упражнение 329 (Вариант 1) – § 13 – Математика 5 класс – Мерзляк А.Г., Полонский В.Б., Якир М.С.Скачать

Как выглядит 12 угольник?

Двенадцатиуго́льник, додекаго́н (греч. δώδεκα — двенадцать и греч. γωνία — угол) — многоугольник с 12 углами и 12 сторонами. Как правило, додекагоном называют правильный многоугольник, то есть такой, у которого все стороны и все углы равны (в случае додекагона углы равны 150°).

Видео:Как правильно решить задание про четырёхугольник? / Разбор заданий на ОГЭ по геометрииСкачать

энциклопедия жизненных ответов

мы стараемся находить самые интересные вопросы и давать на них исчерпывающие ответы. заходите к нам почаще и вы всегда будете находить для себя что-нибудь новое и интересное.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

темы вопросов

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

актуальные комментарии к ответам

Видео:8 класс. Урок 1: ЧетырехугольникиСкачать

Сколько диагоналей у треугольника, четырехугольника, пятиугольника, шестиугольника, восьмиугольника?

Диагональ в многоугольнике (полиэдре) — отрезок, соединяющий любые две несмежные вершины, другими словами, вершины, не принадлежащие одной стороне многоугольника (одному ребру полиэдра).

У полиэдров различают диагонали граней (рассматриваемых как плоские многоугольники) и пространственные диагонали, выходящие за границы граней. У полиэдров, имеющих треугольные грани есть только пространственные диагонали.

Диагоналей нет у треугольника на плоскости и у тетраэдра в пространстве, так как все вершины этих фигур попарно связаны сторонами (ребрами).

Количество диагоналей N у многоугольника просто вычислить по формуле:

где n — число вершин многоугольника. По этой формуле несложно отыскать, что

Сколько вершин, ребер и граней у куба (гексаэдра)?

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Добавить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

📺 Видео

Свойства правильного шестиугольника. Сравнение площадей. Разбор задачи из стереометрии.Скачать

Глава 1. #8класс §1 Многоугольник. #конспект #геометрия учебник 2018 стр 11 В. В. КазаковСкачать