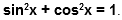Если посмотреть на числовую окружность , то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).

(() (frac) (;2π)) — четвертая четверть
- Почему так важно определять какой четверти принадлежит угол?
- Про непостоянство четвертей:
- Единичная окружность
- Единичная окружность в тригонометрии
- Единичная числовая окружность на координатной плоскости
- п.1. Понятие тригонометрии
- п.2. Числовая окружность
- п.3. Градусная и радианная мера угла
- п.4. Свойства точки на числовой окружности
- п.5. Интервалы и отрезки на числовой окружности
- п.6. Примеры
- 🎥 Видео
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Почему так важно определять какой четверти принадлежит угол?
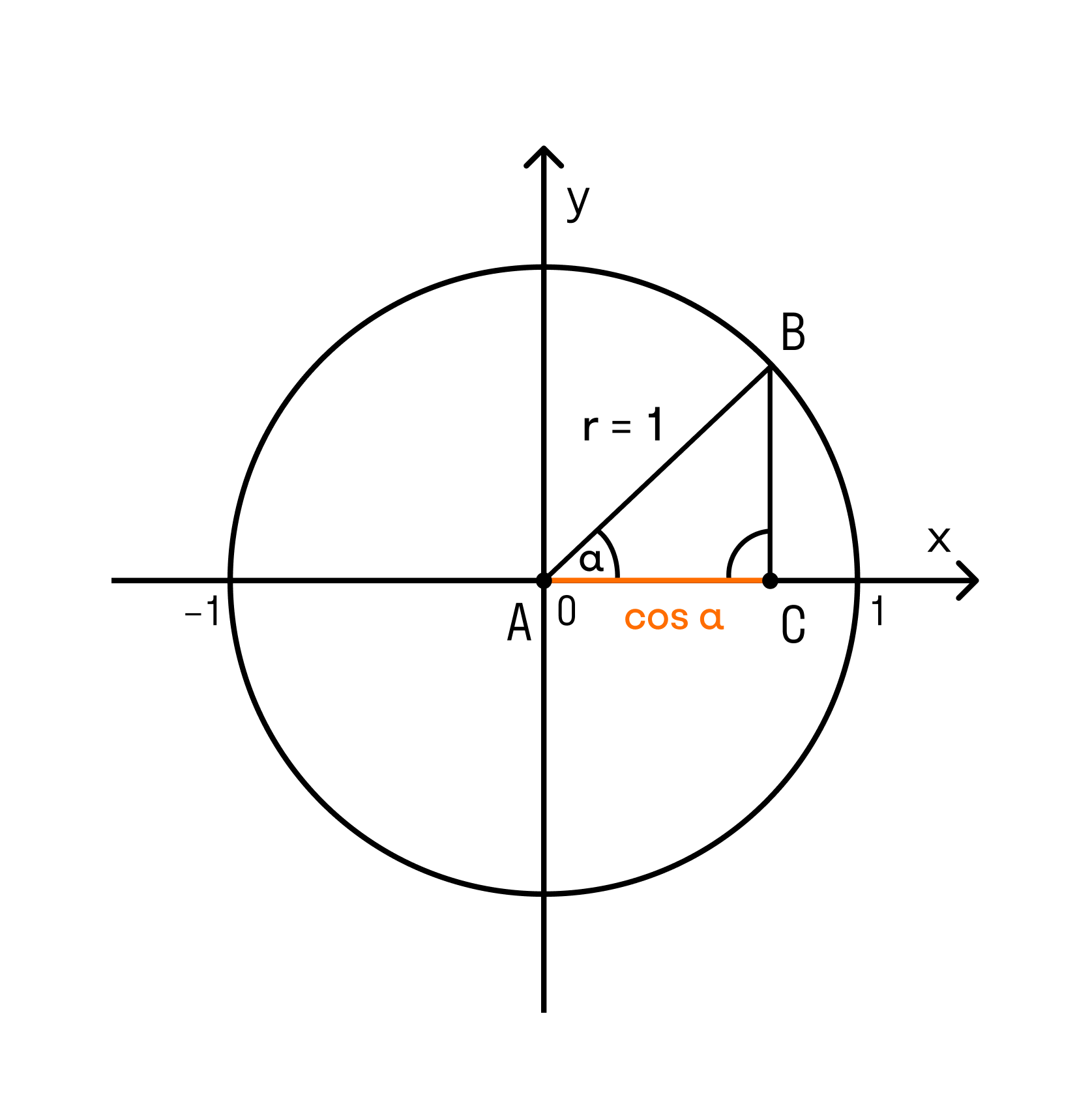
Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций .
Например, для любого угла из второй четверти — синус положителен, а косинус , тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны.
Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.
Пример (ЕГЭ):
 ((0;-) (frac) ()) — четвертая четверть Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную. Видео:В какой четверти находится точка единичной окружности, полученная при повороте Ро(1;0) на угол...Скачать  Единичная окружностьО чем эта статья: 10 класс, ЕГЭ/ОГЭ Статья находится на проверке у методистов Skysmart. Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать  Единичная окружность в тригонометрииВсе процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение. Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице. Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра. Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью. Поясним, как единичная окружность связана с тригонометрией. В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности. Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA. Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности. Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так: Радиан — одна из мер для определения величины угла. Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса. Число радиан для полной окружности — 360 градусов. Длина окружности равна 2πr, что превышает длину радиуса в 2π раза. Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан. Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса. Уравнение единичной окружности При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество: Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам. Видео:Тригонометрическая окружность. Как выучить?Скачать  Единичная числовая окружность на координатной плоскостип.1. Понятие тригонометрииТригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами. Базовым объектом изучения в тригонометрии является угол. Предметом изучения тригонометрии как раздела математики выступают: п.2. Числовая окружностьМы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
п.3. Градусная и радианная мера углаУглы можно измерять в градусах или в радианах. В целом, более обоснованной и естественной для измерения углов является радианная мера.
п.4. Свойства точки на числовой окружностиПостроим числовую окружность. Обозначим O(0;0), A(1;0)
п.5. Интервалы и отрезки на числовой окружностиКаждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.
п.6. ПримерыПример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2. Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^=frac.\ EC=60^=frac.\ AE=EC+CD=90^+30^=120^=frac.\ ED=EC+CD=60^+90^=150^=frac. end Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac; frac; frac; frac).
Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac; 5pi; frac; frac).
Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.
(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb)), запишите количество полученных базовых точек.
Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам. 🎥 ВидеоАлгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать  Найти координаты точки единичной окружности полученной при повороте точки Ро(1;0) на угол π, 450°...Скачать  Изобразить на единичной окружности точку.Скачать  Найти знак тригонометрической функции (bezbotvy)Скачать  Числовая окружностьСкачать  Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать  Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать  стр 15 #1.14 Алгебра 10 класс. Определите, углом какой четверти является уголСкачать  Период тригонометрических функций тангенс и котангенс в градусах В какой четверти находится угол поСкачать  Период синуса и косинуса в градусах. В какой четверти находится угол поворота. 8-11 класс.Скачать  3 четверть. 9 класс. Алгебра. Углы на единичной окружностиСкачать 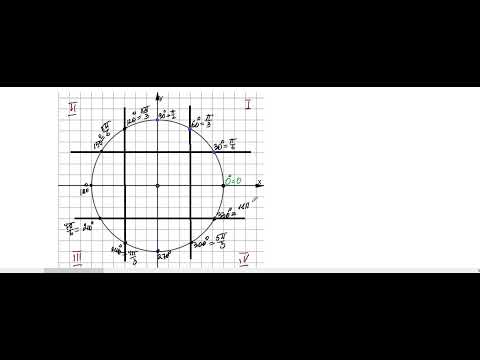 Математика 10 класс.Построение точек на числовой окружности 10 классСкачать 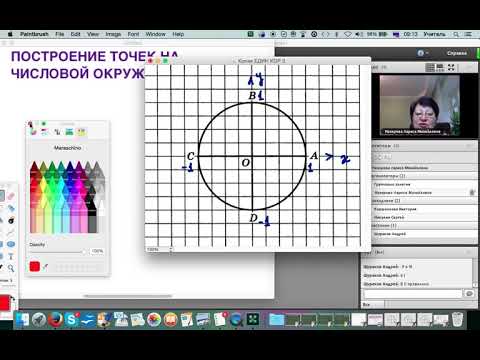 6 Линия тангенсов и линия котангенсовСкачать  Попадание точки в заданную область. Круг в круге. Уроки программирования на С++.Скачать  ЗНАЧЕНИЯ СИНУСА И КОСИНУСА НА ОКРУЖНОСТИСкачать  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||