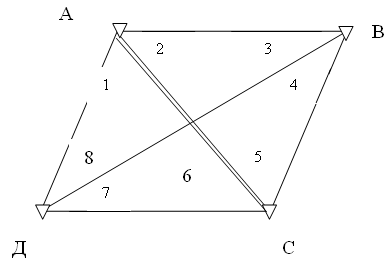
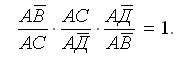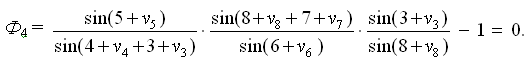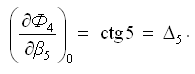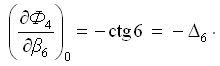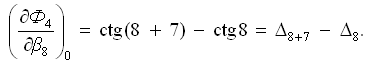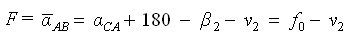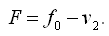Для определения координат пунктов В и Д в геодезическом четырехугольнике (рис. 2) измерено равноточно (рi = 1) восемь углов между сторонами и диагоналями. Результаты измерений помещены в табл. 5.
Рис. 2. Геодезический четырехугольник
| № углов | Измеренные углы βi | № углов | Измеренные углы βi |
| 77°35′ 46,3″ | 36°00′ 05,7″ | ||
| 57° 00′ 57,0″ | 46° 29′ 49,3″ | ||
| 27° 22′ 57,6″ | 37° 54′ 10,8″ | ||
| 59° 35′ 57,7″ | 18° 00′ 15,7″ |
Определим число независимых условных уравнений.
Число необходимых измерений в линейно-угловой сети равно удвоенному числу вновь определяемых пунктов, t = 2 · 2 = 4. Число избыточных измерений
r = n — t = 8 — 4 = 4.
В геодезическом четырехугольнике имеют место четыре независимых условных уравнения, 3 — условных уравнения фигур и 1 — полюсное.
Составим условные уравнения связи.
Условное уравнение фигур: сумма углов плоского треугольника после уравнивания минус 180° равна нулю.
Обозначим βi = i. Для трех треугольников, например, ΔАВС, ΔАДС, ΔАВД условные уравнения фигур будут иметь вид:
Полюсное условное уравнение: отношение сторон, сходящихся в одной точке (полюсе), после уравнивания равно единице. Если полюс — точка А, то
По теореме синусов, отношение сторон заменяют отношением синусов противолежащих углов:
Составим условные уравнения поправок.
Условные уравнения фигур имеют линейный вид. Для перехода к условным уравнениям поправок следует вычислить невязки, которые равны суммам измеренных углов в треугольнике минус 180°.
Полюсное условное уравнение связи приводят к линейному виду разложением в ряд Тейлора
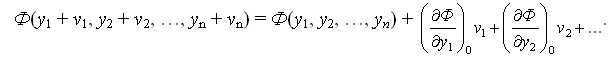
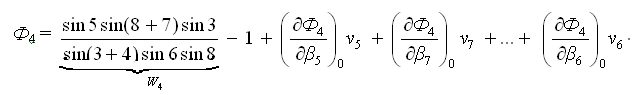
Частная производная функции Ф4 по аргументу β5 (углу числителя):
Частная производная функции Ф4 по аргументу β6 (углу знаменателя):
Частная производная функции Ф4 по аргументу β8 (углу числителя и знаменателя):
С учетом размерности поправок и невязки полюсное условное уравнение поправок имеет вид:
Умножив на ρ″, получим
Определение коэффициентов Δi и невязки w″4 полюсного условного уравнения выполним на ПК по программе Polus.exe. Исходной информацией к программе являются углы числителя и знаменателя полюсного условного уравнения (табл. 6).
| . | Числитель | . | . | Знаменатель | . |
| № углов | βi | Δi | № углов | βi | Δi |
| 36°00′ 05,7″ | 1,38 | 3+4 | 86°58′ 55,3″ | 0,05 | |
| 8+7 | 55° 54′ 26, 5″ | 0,68 | 46° 29′ 49,3″ | 0,95 | |
| 27° 22′ 57,6″ | 1,93 | 18° 00′ 15,7″ | 3,08 |
Полюсное условное уравнение поправок принимает вид:
Составим весовую функцию.
— дирекционный угол стороны АВ, вычисленный по результатам уравнивания.
Итак, получена следующая система условных уравнений поправок:
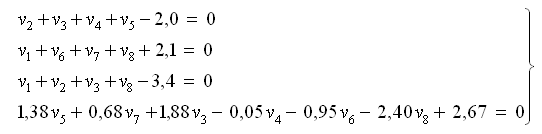
Коэффициенты условных уравнений и функции
| № измерения | a | b | c | d | f | ν |
| . | ||||||
| -1 | . | |||||
| +1.88 | . | |||||
| -0.05 | . | |||||
| +1.38 | . | |||||
| -0.95 | . | |||||
| +0.68 | . | |||||
| -2.40 | . |
и весовая функция:
Коэффициенты условных уравнений и функции поместим в табл. 7.
Дальнейшее решение задачи выполните на ПК по программе KORREL.EXE. Таблицу коэффициентов условных уравнений вводите по столбцам.
Выпишите с экрана:
1. Значения поправок к результатам измерений в столбец ν табл. 7.
2. Среднюю квадратическую ошибку измерения — m.
3. Обратный вес 1/PF и среднюю квадратическую ошибку функции — mF.
Вычислите уравненные значения углов 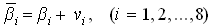
Дата добавления: 2016-06-24 ; просмотров: 3718 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Уравнивание измеренных углов в геодезическом четырехугольникеСкачать

Коррелатный способ уравнивания
Приведенная выше система уравнений (14.8) имеет нелинейный вид. В математике не существует способов решения таких систем нелинейных уравнений. В связи с этим данную систему уравнений раскладывают в ряд Тейлора, ограничиваясь только первыми членами разложения с учетом того, что значения поправок у достаточно малы (на основании выдержанных при измерениях допусков по точности) , и вторые их степени будут весьма малыми, так что ими можно будет пренебречь. В результате уравнения (14.8) преобразуются к виду:
где i — номер измеренной величины (х); j — номер условного уравнения (или функции ф).
С учетом введенных обозначений получим:
В обозначениях гауссовых сумм:
Равенства (14.80) и (14.81) называются условными уравнениями поправок.
Следует иметь в виду, что формулы (14.79) не используются, если известно, что система уравнений (14.8) имеет линейный вид, т. е. коэффициенты a(j известны.
Для решения задачи уравнивания способом Лагранжа необходимо составить следующую функцию:
где Xj — неопределенные множители Лагранжа.
Тогда функцию (14.82) можно записать со значениями коррелат:
Для определения поправок у, при которых функция (14.83) достигает минимума, найдем частные производные по аргументам у и приравняем их нулю:
Из полученной системы уравнений следует, что
где q,, = ——обратный вес измерения с индексом z.
Уравнения (14.85) и (14.86) называют коррелатными уравнениями поправок.
Число коррелат всегда равно числу условий. В результате образуется система коррелатных уравнений поправок у, содержащая п неизвестных поправок у и г неизвестных коррелат kjt состоящая из п линейных уравнений.
Опуская промежуточные, хотя и важные преобразования (вывод можно посмотреть в соответствующей геодезической литературе), основанные на методе наименьших квадратов, приведем т. н. нормальные уравнения коррелат, в которых число неизвестных равно числу уравнений:
В уравнениях (14.87) неизвестными являются коррелаты kt, а свободными членами — свободные члены уравнений поправок (14.80) и (14.81).
Как видно, при каждом параметре (неизвестном) ki в уравнениях (14.87) стоит коэффициент в виде гауссовой суммы. Представим указанные коэффициенты в развернутом виде с помощью таблицы коэффициентов уравнений поправок (табл. 14.3).
Развернутый вид коэффициентов [qaiai],[qala2. [qarar, в которых индекс при коэффициентах а — это второй индекс коэффициентов условных уравнений поправок:
Матрица коэффициентов линейных уравнений
 |  |  |  |  | |||
 |  |  |  |  |  |  | |
 |  |  |  |  |  |  | |
 |  |  |  |  |  |  | |
 |  |  |  |  |  |  |  |
 |  |  |  |  |  |  |  |
 |  |  |  |  |  |  |  |
 |  |  |  |  |  |  |  |
 |  |  |  |  |  |  |  |
Рассмотрим подробнее принцип вычисления коэффициентов bjj при коррелатах kj в нормальных уравнениях коррелат.
1- е уравнение коррелат
Коэффициент при к] равен сумме произведений обратных весов и квадратов коэффициентов первой строки матрицы.
Коэффициент при к2 равен сумме произведений обратных весов и коэффициентов 1-й и 2-й строк матрицы.
Далее производятся последовательные действия для всех остальных строк до последней строки. Так, коэффициент при кг равен сумме произведений обратных весов и коэффициентов 1-й и г-й строк матрицы.
2- е уравнение коррелат
Коэффициент при к] равен сумме произведений обратных весов и коэффициентов 2-й и 1-й строк матрицы.
Коэффициент при к2 равен сумме произведений обратных весов и квадратов коэффициентов 2-й строки матрицы.
Коэффициент при к3 равен сумме произведений обратных весов и коэффициентов 2-й и 3-й строк матрицы и т. д. до последней строки.
Аналогично выполняются вычисления для остальных строк.
г-е уравнение коррелат
Коэффициент при к< равен сумме произведений обратных весов и коэффициентов r-й и 1-й строк матрицы.
Коэффициент при к2 равен сумме произведений обратных весов и коэффициентов г-й и 2-й строк матрицы и т. д.
Коэффициент при кг равен сумме произведений обратных весов и квадратов коэффициентов г-й строки матрицы.
Таким образом получают уравнения коррелат вида:
Можно заметить, что коэффициенты Ъ с обратными индексами равны между собой, т. е. Ь12 = Ь21, Ь35 = Ь53ит. п. Так называемые диагональные коэффициенты Ьп представляют собой сумму произведений обратных весов и квадратов коэффициентов a j-й строки, т. е. они всегда положительные. Коэффициенты Ь с обратными индексами располагаются с разных сторон от диагональной строки. В связи с этим достаточно вычислить диагональные коэффициенты и все коэффициенты, стоящие справа от диагонали, а далее дополнить уравнения недостающими коэффициентами Ь, записав их такими же, как и коэффициенты с обратными им индексами.
Решение систем линейных уравнений (14.89) выполняется различными способами, рассмотренными в § 135, и другими способами, которые здесь не приведены, но все они, как можно было убедиться из приведенных примеров, весьма громоздкие и требуют значительных затрат времени. Единственным спасением может быть использование специальных программ расчетов на компьютере.
Полученные из решения уравнений (14.89) коррелаты ^используются для вычисления поправок у по формулам (14.85) или (14.86). После введения поправок в измеренные величины получают уравненные значения измеренных величин (14.7).
При оперировании численными значениями коэффициентов условных уравнений, коррелат, весов (обратных весов) и т. п. необходимо иметь в виду следующее:
- — значения весов и обратных им величин вычислять до 0,01 — 0,001 единиц;
- — значения коэффициентов а, Ь и коррелат it вычислять до 0,001 — 0,0001 единиц;
- — чаще всего невязки Wnpn обработке плановых построений выражают в дециметрах, в высотных сетях — в миллиметрах, угловые невязки и поправки выражают в секундах, десятых и сотых долях секунды.
Суммируя сказанное выше, приведем последовательность решения задачи уравнивания коррелатным способом.
Шаг 1. Для данного геодезического построения в системе л результатов х. имеющих веса рг, определяют число к независимых и число г избыточных измерений.
Шаг 2. Составляют математические соотношения (условные уравнения) вида (14.5) с учетом следующих основных требований:
- — все условные уравнения должны быть независимыми, т. е. ни одно из них не должно быть следствием другого (других);
- — число уравнений должно быть равно числу избыточных измерений г;
- — условные уравнения должны иметь возможно простой вид. Шаг 3. Условные уравнения приводят к линейному виду, для чего
выполняют их дифференцирование и находят коэффициенты a(j (14.79) как частные производные функций ф; по аргументам хг
Находят свободные члены Wj уравнений, т. е. невязки в полученных уравнениях после подстановки в них измеренных значений хг Составляют таблицу (матрицу) коэффициентов ai> и обратных весов д( (табл. 14.3).
Шаг 4. Находят коэффициенты Ь^( 14.88) нормальных уравнений коррелат (14.89) по алгоритму, изложенному выше, и решают полученную систему линейных уравнений.
После получения значений коррелат kj из решения уравнений обязательно необходимо выполнить контроль вычислений. Для этого значения коррелат подставляют в исходные уравнения (14.89) и проверяют выполнение условия. Незначительные отступления от условия уравнения допускаются, они возникают из-за округления результатов вычислений.
Шаг 5. Составляют, пользуясь табл. 14.3, условные уравнения поправок v, (14.80), (14.85) (или (14.86). Для значений поправок, например, получим:
Вычисляют поправки к измеренным величинам.
Шаг 6. Вычисляют уравненные значения х( (14.7).
Контроль уравнивания осуществляют подстановкой х/ в условные уравнения (14.9). При правильном решении задачи все условные уравнения должны иметь указанное решение. Допускаются незначительные отклонения от указанных условий, они возникают из-за округления результатов вычислений.
После выполнения контроля значения х( округляют с необходимой точностью и вычисляют искомые величины (координаты, высоты и т. п.).
Если условные уравнения изначально существенно нелинейны и при разложении в ряд Тейлора, вообще говоря, недостаточно ограничиваться первыми членами разложения, то условия (14.9) могут не выполниться. В этом случае производят второе приближение уравнивания, считая уравненные из первого приближения значения х! измеренными, а свободными членами Wj — остаточные невязки в уравнениях (14.9).
В § 137 рассмотрены примеры уравнивания различных геодезических построений коррелатным способом.
Видео:Уравнивание ГРО. ГЕОДЕЗИЧЕСКИЕ РАБОТЫСкачать
Уравнивание геодезического четырехугольника
Автор работы: Пользователь скрыл имя, 02 Апреля 2013 в 10:23, реферат
Краткое описание
Исходные данные: ХВ и YВ; ХD и YD.
В геодезическом четырехугольнике измерены восемь углов на четырех точках (рисунок 32). Углы нумеруются цифрами 1-8 по ходу часовой стрелки. Необходимо определить координаты пунктов А и С, а также дирекционные углы и длины сторон.
Вложенные файлы: 1 файл
Видео:Коррелатный способ. Решение системы условных уравненийСкачать

Уравнивание геодезического четырехугольника.docx
Уравнивание геодезического четырехугольника
В геодезическом четырехугольнике измерены восемь углов на четырех точках (рисунок 32). Углы нумеруются цифрами 1-8 по ходу часовой стрелки. Необходимо определить координаты пунктов А и С, а также дирекционные углы и длины сторон.
1. В геодезическом четырехугольнике возникают следующие условия:
— сумма всех восьми углов в четырехугольнике должна быть равна 360°;
— геодезический четырехугольник рассматривается как центральная система с фиктивным полюсом – точкой О пересечения диагоналей;
— в фиктивных треугольниках АВО, DОС, ВСО и АОD должны существовать следующие условия суммы углов: 1+2 = 5+6; 3+4 = 7+8;
— все измеренные углы можно рассматривать как связующие углы треугольников центральной системы, следовательно, возникает полюсное условие.
условий фигур – 3;
условие полюса – 1.
2. Невязки за условия фигур вычисляются по формулам:
w1 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 — 360°;
w2 = 1 + 2 – 5 – 6; (209)
Допустимая невязка wдоп = 2,5 mb Ön; (210)
Первичные поправки V¢ вычисляем по формулам:
Вычисление поправок контролируется: их сумма в четырехугольнике должна равняться невязке с обратным знаком.
3. За полюс принята точка пересечения диагоналей. Тогда условное уравнение полюса, как и в центральной системе, можно выразить формулой:
wП = [ ( lg sin1 + lg sin3+ lg sin5 + lg sin7) –
– ( lg sin2 + lg sin4+ lg sin6 + lg sin8) ] 10 6 (212)
где b — это изменение логарифма синуса угла при изменении самого угла на одну секунду в шестом знаке логарифма.
Для вычисления вторичных поправок за условие полюса определяем коррелату К
Введением вторичных поправок заканчивается процесс уравнивания горизонтальных углов. После чего решением треугольников находят стороны, вычисляют дирекционные углы и приращения координат. Полученные невязки приращений распределяют пропорционально длинам сторон и вычисляют окончательные координаты пунктов.
🎦 Видео
Подготовка измерений к уравниванию или предобработка. Основные теоретические моменты.Скачать

Уравнивание нивелирных сетей параметрическим методом.Скачать

Основы параметрической формы метода наименьших квадратов (МНК) на примере уравнивания опорных сетей.Скачать

Простой способ подобрать геодезические пункты для работы.Скачать

Сбор подписей за выдвижение Надеждина. Орешкин*, Кынев. Утро с Роменским* и Баблоян / 23.01.24Скачать

04 Геочайник - Угловые величины в геодезииСкачать

ЧАСТЬ 1. Экзаменационные задачи по инженерной геодезии для 1 курсаСкачать

От Фалеса к триангуляционной сетиСкачать

Геодезическая разбивочная основа. Подготовительные работы. ГЕОДЕЗИЧЕСКИЕ РАБОТЫСкачать

Простой и легкий способ создания условной системы координат в AutoCad в геодезииСкачать

Прямая геодезическая задача. Формулировка. ОпределениеСкачать

Уравнивание свободных маркшейдерских и геодезических сетей параметрическим методом.Скачать

Определяем пункты ГРО. ГЕОДЕЗИЧЕСКИЕ РАБОТЫСкачать

Решение обратной геодезической задачиСкачать

Уравнивание геодезических сетей и оформление топографических планов (30-10-2013)Скачать

Вычерчивание фактических и проектных горизонталей на площадкеСкачать

Геодезия. ГРО и сгущение сетиСкачать