Как построить вектор куба

Однажды от своих родственников я услышал такую фразу: «Люди на МехМате МГУ не могут быть нормальными, ведь они могут представить себе 7-ми мерное пространство!»

И когда я это услышал, мне тоже показалось, что это — что-то нереальное, невозможное. Но вот прошли года, и когда я снова услышал эту фразу, меня повергло в шок — я тоже могу представить 7-ми мерное пространство и не сломаться. Или я уже не из тех, кто может спокойно гулять по улицам?

Ответ, казалось бы, так прост и так несложен, но многие просто не задумывались над этим вопросом, и поэтому это кажется чем-то странным и нереальным.

Так вот, в данной статье я хочу задуматься, ответить и рассказать, что же за простой ответ скрывается под таким странным вопросом: «Что такое 7-ми мерное пространство?»

В данной статье я попытаюсь рассказать свое понимание многомерного пространства, как я представляю его в своей голове. Возможно, что-то может показаться немного нестрогим – так оно и есть, понятное дело, я пропускаю некоторые детали и пытаюсь писать максимально научно-популярным языком. Надеюсь, Вам понравится мое видение многомерного пространства и Вы почувствуете ту же красоту математики, которую я вижу в данной иллюстрации чего-то непонятного.

Я постараюсь описать некоторые детали с самых азов, вкратце, чтобы любой желающий мог бы разобраться в моих словах.

Видео:Как строить сечение куба? Стереометрия. 10-11 класс | Математика | TutorOnlineСкачать

Оглавление

Выражаю благодарность @AnnRemi за помощь в редактировании и опускании на землю моих амбиций по статье.

Видео:Координаты точки и координаты вектора 1.Скачать

Начало начал, или что такое вектор

Вектор: наверняка каждый сталкивался с таким понятием в школе, это не сложно и очень понятно.

Вектором называется направленный отрезок или просто луч, имеющий конкретную длину.

То есть если луч, как и прямая — понятие бесконечное и простирается вправо и влево в бесконечность, то вектор — понятие ограниченное длиной. Обычная стрелочка, нарисованная на бумаге — вектор. Линейкой мы можем измерить длину этой стрелочки, а направление «этой длины» показывает сама стрелка. Важно понимать, что нам не важно, откуда отложен наш вектор, из какой точки. Нужно знать только длину и направление. Обычно мы изображаем наш вектор в осях координат — так удобно находить его параметры.

Вектор AB в осях координат

Для удобства мы отмечаем на оси Х и на оси У проекции наших точек. Теперь, чтобы посчитать длину нашего вектора достаточно воспользоваться Теоремой Пифагора

Направление, или угол наклона относительно оси Х легко посчитать, например, через тангенс, ведь мы знаем длины обоих катетов треугольника

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Понятие радиус-вектора

Как мы уже увидели, в векторе нам важны только две вещи: длина и направление, так зачем его рисовать где-то в середине нашей координатной плоскости. Давайте сместим наш вектор к началу оси координат. Тогда нам надо будет хранить только координаты конца вектора — а координаты начала вектора у нас будут нулевыми.

Смещенная ось координат

Так теперь надо будет меньше мучаться — храним в векторе просто координаты его конца.

Такие вектора называются в школе радиус-векторами, но в дальнейшем мы будем все вектора брать радиус-векторами, ведь, как мы помним, все вектора имеющие одно направление и одну длину — одинаковые, один и тот же вектор, так почему бы нам не взять тот, который удобнее всего записывается.

Видео:Координаты вектора. 9 класс.Скачать

Трехмерный вектор

Если мы уже разобрались, что такое вектор на плоскости — давайте перейдем к вектору в трехмерном пространстве — в объемном мире.

Достаточно просто представить себе стрелку в объеме — достаточно вспомнить, как Вы что-то измеряли рулеткой. Прислонили конец к шкафу, другой к полу, и померили его диагональ. Ну или не шкаф. каждому свое. Но точно можно сказать, что такое трехмерный вектор.

Но давайте немного формулизируем то, что мы поняли. Представим трехмерные координаты и в них наш радиус-вектор AB.

Трехмерный вектор AB

Понятно, что нам теперь совсем не хватит двух координат для описания вектора AB. Так что давайте добавим третью координату, просто дописав ее в конце.

Хммм. интересно, а по какому признаку мы можем вот так просто приписывать координаты? Может, можно просто так добить вектор до семимерного? Ну в принципе, нас никто остановить не может, и мы именно так и поступим, но сначала немного окунемся в линейную алгебру.

Видео:№402. Даны координаты четырех вершин куба ABCDA1B1C1D1: А (0; 0; 0), В (0; 0; 1), D (0; 1; 0)Скачать

Базис в пространстве

Базис — упорядоченный набор векторов в векторном пространстве, такой, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого набора.

Линейная комбинация – это сумма некоторого набора элементов множества с допустимыми коэффициентами.

Также я собираюсь использовать в дальнейшем удобное следствие определения базиса: мы можем расширять наш базис с помощью векторов, линейно независимых с базисными.

Что значит расширить базис? Добавить еще один вектор, тем самым расширяя наше пространство еще в одном направлении.

Выше мы уже научились строить трехмерное пространство — просто объемный мир, в котором мы живем. Давайте попробуем расширить наш базис. Самым очевидным расширением базиса будет добавление времени, как еще одного параметра. То есть четырехмерное измерение — это объемная жизнь с привязкой ко времени. Ну разве это не похоже на обычную жизнь человека? То есть все это время мы жили в четырехмерном пространстве, а не трехмерном.

И, как не сложно заметить, время линейно независимо от объема, то есть наше расширение базиса вполне корректно.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

7ми мерное пространство и почему только 7ми?

Как нам представить 5ти мерное пространство? Но мы же уже сказали, что на самом деле пространство — это то, что его задает — базис. То есть давайте теперь мыслить о пространстве, как о наборе параметров каждой его точки. Например для трехмерного объекта мы помним 3 координаты в пространстве — по x, y, z. И у нас это не вызывает диссонанса.

Давайте к координатам припишем еще и время, в которое у нас наблюдалась данное расположение тел. Например, у нас катится шар и мы следим за положением его центра. В момент времени 0 шар покоился. В 0,0. 01 он уже сместился. В момент времени 9. 9,0 он уже находится в совершенно другом месте. Но зачем нам так думать? Пусть эта точка шара существует одновременно везде, где проехался шар, только мы будем помнить, что в каждой точке мы еще приписываем время, когда шар был именно в данной позиции. Вот Вам и 4х мерное пространство — не сложно.

Казалось, так можно навесить еще какие-то параметры, такие как скорость ветра, влажность воздуха, сила трения и так далее, но давайте не будем извращаться и перейдем к более жизненному понятию.

Допустим у нас есть разные гаечки (прошу прощения, если я ошибусь в параметрах или названиях, я совсем не инженер). Для удобной фасовки и продажи гаек надо распределить их на группы одинаковых. Но как мы будем их отличать? Давайте запишем какой-то набор параметров (не претендующий на правильность):

Сплав метала гайки

Внутреннее сечение гайки

Внешняя форма гайки

Направление резьбы гайки

Максимальная нагрузка на гайку

Самозажимающаяся ли гайка?

Максимальная температура, при которой гайка выдерживает достаточную нагрузку

Понятно, что таких параметров может быть сколь угодно много. Но мы остановимся на 7ми — именно столько заявлено в заголовке статьи. Важно помнить! каждый параметр обязан быть независим от любого предыдущего. В нашем случае это условие выполняется: направление резьбы никак не зависит от сплава метала или от внутреннего сечения гайки. И так с каждым из параметров.

То есть только что мы создали свой, очень странный базис, где элементами нашего пространства выступают гайки, и мы их можем удобно расфасовать. Это и есть элементарное представление нашего 7ми и не только 7ми, но и большего, пространства.

Видео:Как построить точки в системе координат OXYZСкачать

Пространство — не куб!

В заголовке статьи я обещал куб, но пока говорил только о пространстве. Давайте определим, что же такое куб.

Например, в 2х мерном пространстве куб, очевидно,- это квадрат. То есть объект с точками вершинами:

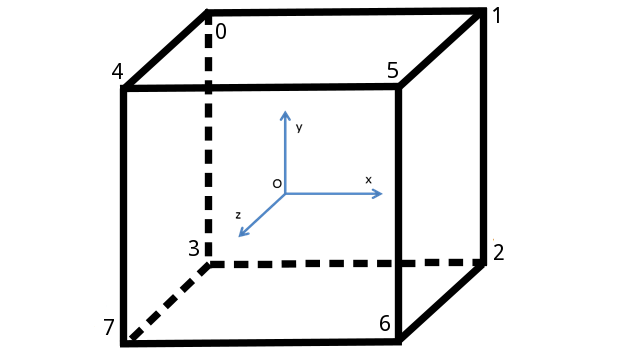
В трехмерном пространстве куб — есть куб. С координатами:

Как мы заметили, в двумерном пространстве у куба 4 = 2^2 вершин, в трехмерном 8 = 2^3. Совпадение? Маловероятно. Ну и правильно, ведь из простейшей комбинаторики мы помним, что количество вершин равно 2^n для n-мерного куба. Ведь мы либо берем каждый из базисных n векторов, либо нет.

Тогда для построение 7ми или n-мерного куба нам достаточно взять точки с фиксированными координатами (0 или a) по каждой из осей.

Видео:Построение сечения куба по трем точкамСкачать

Интересный факт

Именно из-за удобства понимания и описания n-мерного куба мы меряем любую n-мерную поверхность таким способом. Площадь квартиры с помощью квадратных метров, длину прямой в метрах, объем в кубических метрах. Это все кубы разной размерности. И в математике нам очень удобно оперировать именно такими понятиями. Примерно так мы определяем меру множества, которая очень важна для теории интегралов, теории вероятностей, теории меры и очень много где еще.

Видео:Сложение и вычитание векторов. Практическая часть. 11 класс.Скачать

Послесловие

Как Вы, наверное, заметили, я привожу совсем иное понимание многомерного куба, в отличие от общепринятого.

Не то, чтобы красивые картинки многомерных кубов не вызывали у меня восхищения – совсем нет, но в этом есть что-то нереальное, непонятное и неприложимое. Я совсем не претендую на прикладное значение сортировки гаек, но мне кажется довольно захватывающим такое представление многомерности: как что-то такое далекое может быть таким емким.

4х мерный куб – Тессеракт

На самом деле я просто не имею настолько развитого пространственного воображения: я не понимаю, как можно визуализировать 4х, 5ти и более мерный куб на 2D картинке.

Также такая иллюстрация не позволяет представить, как увеличить пространство еще в одном направлении. Так что именно данная тема не рассматривается в моей статье, но, если Вас заинтересовал Тессеракт, есть огромная куча других, очень интересных, статей, описывающих его построение и даже расширение.

Видео:Сечение куба. Как строить сечение куба. Метод следов. Метод параллельностиСкачать

Как построить вектор куба

В этой статье мы научимся рисовать простой 3D объект — куб. Также мы запрограммируем анимацию куба и виртуальную камеру, позволяющую взглянуть на куб глазами зрителя.

Видео:Как строить сечения параллелепипедаСкачать

Содержание

Видео:Сложение векторов. 9 класс.Скачать

Вершины куба

В чём OpenGL измеряет расстояния в трёхмерном мире? В 2D графике всё понятно: у нас есть пиксели. На трёхмерной проекции объекты одинакового размера могут дать разные проекции из-за перспективного искажения: чем дальше поверхность или линия, тем она меньше. Поэтому OpenGL измеряет расстояния в единицах измерения, не уточняя, в каких именно. Вы можете измерять в метрах, попугаях или в футах — на картинке это не имеет разницы, потому что исходные размеры не совпадают с проекциями.

Кроме того, трёхмерные тела поддаются преобразованиям. Поэтому мы будем рисовать только единичный куб и не станем заботиться о поддержке масштаба, вращения и положения центра куба. Единичный куб лежит в координатах от -1 до +1, т.е. каждое ребро имеет длину 2.

Видео:Как строить сеченияСкачать

Триангуляция куба

После того, как выписали список вершин куба, следует разпределить вершины по треугольникам. У куба 6 квадратных граней, их можно описать 12-ю треугольниками. При этом вершины каждого треугольника следует перечислять по часовой стрелке для наблюдателя, смотрящего снаружи куба на этот треугольник. В противном случае треугольник станет поверхностью, видимой изнутри куба, что нарушает физические законы.

Процесс разделения поверхности на треугольники называют триангуляцией (англ. triangulation). Для упрощения этого процесса сделаем визуализацию куба с вершинами, нумерованными в том же порядке, в котором они были перечислены ранее:

Теперь, глядя на иллюстрацию, можно перечислить все 12 треугольников, составляющих 6 граней.

Видео:Математика это не ИсламСкачать

Рисование в Immediate Mode

Для непосредственного рисования граней куба мы применим не самый производительный метод, который к тому же устарел в современных версиях OpenGL: рисование в блоке glBegin/glEnd, также известное как OpenGL Immediate Mode.

Видео:🔥Как строить сечения куба, параллелепипеда через заданные точки?Скачать

Настройка фиксированной камеры

В OpenGL при использовании фиксированного конвейера есть ровно две матрицы, относящихся к трансформациям точек и объектов:

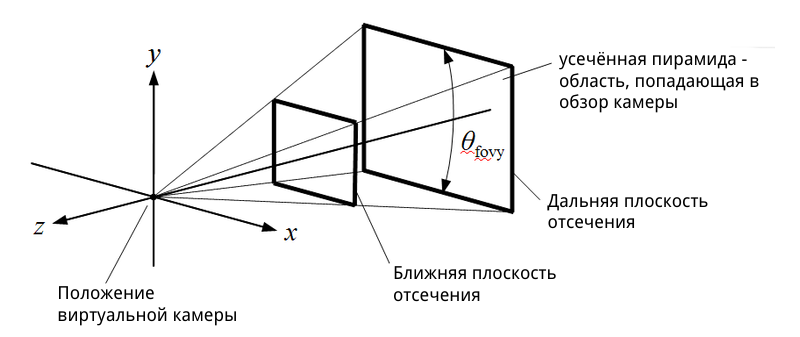
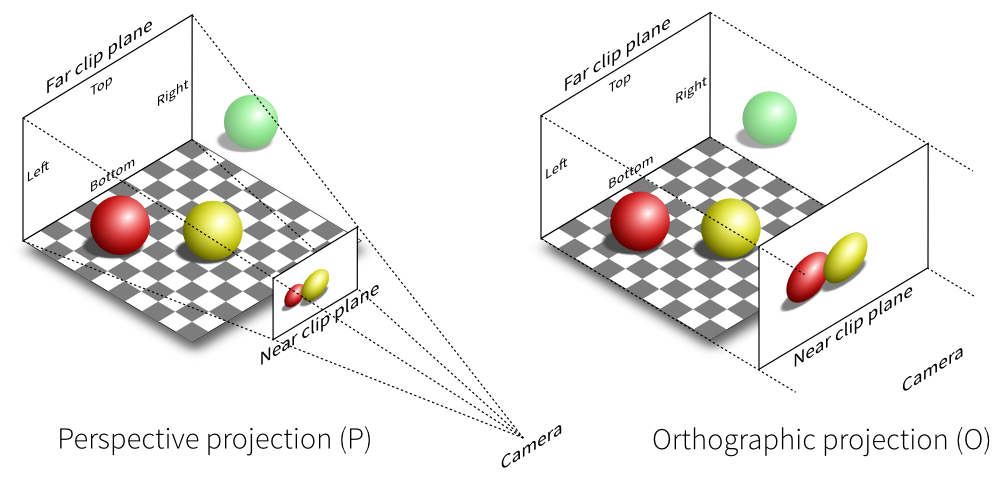
• GL_PROJECTION моделирует ортографическое или перспективное преобразование от трёхмерной усечённой пирамиды (т.е. от области видимости камеры) к трёхмерному кубу с длиной ребра, равной 2 (т.е. к нормализованному пространству).
• GL_MODELVIEW сочетает в себе два преобразования: от локальных координат объекта к мировым координатам, а также от мировых координат к координатам камеры.

За рамками фиксированного конвейера можно использовать столько матриц, сколько захочется — но сейчас мы ограничены. Кроме того, нам приходится смешивать матрицы:

• поведение камеры описывается как ортографическим или перспективным преобразованием, так и положением камеры в мировом пространстве, то есть для моделирования камеры нужны GL_PROJECTION и GL_MODELVIEW одновременно
• c другой стороны, для трансформаций над телами — например, вращения куба с помощью умножения координат на матрицу — нам нужна матрица GL_MODELVIEW.

Обычно при программировании действуют так:

• матрицу GL_PROJECTION обычно настраивают один раз для перспективного преобразования
• матрицу GL_MODELVIEW постоянно модифицируют, когда локальная система координат очередного объекта не совпадает с мировой системой координат

Начнём настройку камеры с GL_MODELVIEW: зададим матрицу так, как будто бы камера смотрит с позиции eye на точку center , при этом направление “вверх” камеры задаёт вектор up :

Для перспективного преобразования достаточно создать матрицу с помощью функции glm::perspective . Она принимает на вход несколько удобных для программиста параметров преобразования: горизонтальный угол обзора камеры (англ. field of view), соотношение ширины и высоты (англ. aspect), а также две граничных координаты для отсечения слишком близких к камере и слишком далёких от камеры объектов. Для лучшего понимания взгляните на иллюстрацию:

Видео:Как построить глубину куба? Видеоурок для начинающих и всем, кто не знал. Основы рисункаСкачать

Решение проблем невидимых поверхностей

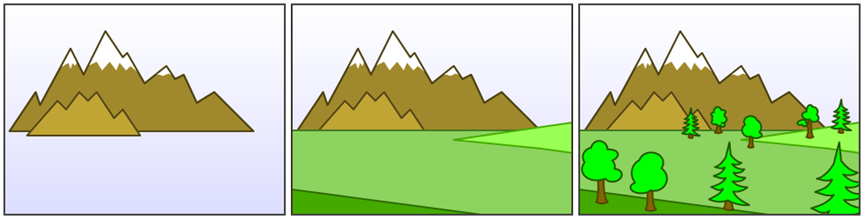
При программном рисовании трёхмерного мира, состоящего из объемных тел с непрерывной поверхностью (англ. solid bodies), возникает вопрос: как не нарисовать невидимые поверхности? Например, на рисунке горы, покрытой лесом, мы не должны увидеть ни деревьев на противоположном к нам склоне, ни поверхности самого склона.

У художников для решения задачи есть свой алгоритм: сначала они рисуют композицию заднего фона, затем сверху покрывают средний фон, и, наконец, выводят передний фон:

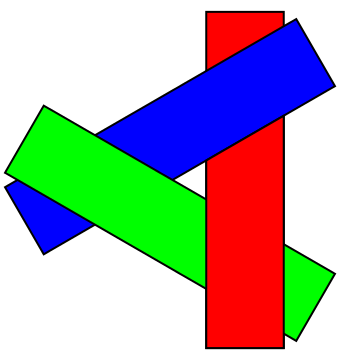
Этот алгоритм так и называется — “алгоритм художника” (англ. painter’s algorithm). В компьютерной графике он иногда применим, но с модификацией: вместо деления объектов на три группы (задний фон, средний фон и передний фон) придётся отсортировать все объекты и вывести их в порядке приближения. К сожалению, не всегда объекты воможно отсортировать: это известно как “проблема художника” (англ. painter’s problem).

Для решения проблемы художника в OpenGL сделано следующее:

• все поверхности представляются как базовые примитивы: в ранних версиях OpenGL это были точки, линии, треугольники и четырёхугольники, а в более поздних остались только треугольники
• используется тест буфера глубины, т.е. модификация алгоритма художника, работающая с неделимыми фрагментами фигур
• используется отсечение граней, развернувшихся невидимой стороной после умножения на матрицы GL_MODELVIEW и GL_PROJECTION

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Тест буфера глубины

Буфер глубины OpenGL — это двумерная матрица дополнительных данных, где каждому пикселю соответствует одно значение float: глубина фрагмента примитива, оказавшегося ближе к пикселю, чем остальные фрагменты примитивов, проецируемые на тот же пиксель. Это позволяет реализовать попиксельный алгоритм художника: после приведения в нормализованное пространство каждая примитивная фигура будет разбита на фрагменты, для которых будет проведён тест глубины.

Фрагмент — это атомарная, то есть неделимая, часть фигуры. Если видеокарта не совершает сглаживание, то один фрагмент станет одним пикселем фигуры.

Тест глубины устроен следующим образом: если фрагмент в нормализованном пространтсве стал ближе, чем последнее значение буфера глубины, то мы выбираем его и обновляем значение в буфере глубины, иначе мы отбрасываем фрагмент. В псевдокоде способ выглядит так:

Как и любой другой буфер OpenGL, буфер глубины следует очищать. Для этого вызов glClear должен получать ещё один флаг GL_DEPTH_BUFFER_BIT :

Также нужно после создания контекста включить режим теста глубины командой glEnable:

Видео:Вычитание векторов. 9 класс.Скачать

Отсечение задних граней

OpenGL рассчитан на дополнительное отсечение невидимых поверхностей, построенное по принципу отсечения задних граней. По умолчанию включён режим, аналогичный вызову glFrontFace(GL_CCW) , и OpenGL делит примитивы на две группы:

• те, вершины которых перечисляются против часовой стрелки (GL_CCW), становятся передними гранями (GL_FRONT)
• те, вершины которых перечисляются по часовой стрелке (GL_CW), становятся задним гранями (GL_BACK)

Вызов glFrontFace(GL_CW) изменит классификацию на обратную: перечисление по часовой даст переднюю грань, перечисление против часовой даст заднюю.

Независимо от того, в каком порядке были заданы исходные вершины, если после всех преобразований грань объёмного тела повёрнута к нам лицевой стороной — порядок обхода сохранится, а если её перекроют другие грани — порядок обхода сменится на противоположный.

Режим отсечения граней можно включить командой glEnable(GL_CULL_FACE) , после чего можно выбрать способ отсечения: убирать задние грани (GL_BACK), передние грани (GL_FRONT) или оба вида граней (GL_FRONT_AND_BACK).

Соберём всю инициализацию состояния OpenGL в метод OnWindowInit, который будет вызываться один раз поле инициализации окна

Чтобы метод OnWindowInit был вызван своевременно, его можно объявить виртуальным в классе CAbstractWindow и вызывать в методе Show:

Видео:№364. Точка К—середина ребра В1С1 куба ABCDA1B1C1D1. Разложите вектор АК по векторам а = АВ,Скачать

Диагностика проблем

При выводе трёхмерных тел встречается ряд типовых ошибок. Если что-то не работает, пройдитесь по следующему чеклисту:

• вы не забыли вызвать glBegin/glEnd до и после вызова glColor/glVertex?
• тело не выпадает из порта просмотра из-за матрицы GL_PROJECTION?
• тело не обрезается дальней и ближней плоскостями отсечения из-за матрицы GL_PROJECTION?
• в массиве индексов нумерация вершин начинается с нуля?
• включён тест глубины и режим отсечения задних граней?
• в массиве индексов вершины примитивов (треугольников и четырёхугольников) перечислены по часовой стрелке для внешнего наблюдателя?

Если всё нормально, то вы получите статичное изображение куба без возможности поменять положение камеры:

Чтобы придать сцене динамику, нам потребуется глубже изучить математические принципы трансформаций точек и векторов в трёхмерном пространстве. Приступим…

Видео:ТЕМА 2. ПОСТРОЕНИЕ КУБА, ЦИЛИНДРА, ШАРАСкачать

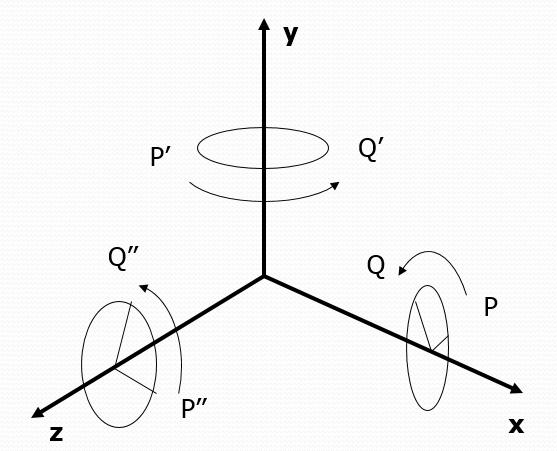
Трёхмерная система координат

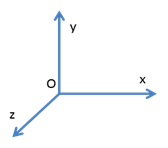
В OpenGL используется правосторонняя система координат, в которых пользователь может задавать вершины примитивов, из которых состоят трехмерные объекты. Правосторонней система координат называется потому, что ее можно образовать при помощи большого, указательного и среднего пальцев правой руки, задающих направления координатных осей X, Y и Z соответственно.

Система координат задаётся точкой отсчёта и координатными осями, которые, в свою очередь, задают направления и длины трёх единичных векторов (1, 0, 0), (0, 1, 0) и (0, 0, 1). Как точка отсчёта, так и координатные оси могут меняться при переходе из одной системы координат в другую.

Например, представьте себе систему координат комнаты, где в качестве центра взята точка в геометрическом центре пола, а ось z указывает вверх, и расстояния измеряются в метрах. Тогда точки головы человека в комнате всегда будут иметь координату z, большую нуля, обычно в диапазоне (1.6; 1.8) . Если же перейти в другую систему отсчёта, где центром служит точка в геометрическом центре потолка, то голова человека в комнате будет иметь отрицательную координату z.

В любой трёхмерной сцене есть система координат, которую можно считать мировой системой коодинат. Это очень удобно: любая точка или вектор в мировой системе координат представляется однозначно. Благодаря этому, если у нас есть несколько локальных систем координат (например: комната, салон автомобиля, камера), и мы знаем способ преобразования из любой системы в мировые координаты, то мы можем спокойно перейти, например, от системы координат комнаты к системе координат камеры:

О локальных системах координат можно сказать следующее:

• для перехода к мировой системе координат всегда есть аффинное преобразование, состоящее из некоторого числа перемещений, вращений и масштабирований
• если точка отсчёта в разных координатах разная, это можно представить перемещением (англ. translate)
• если координатные оси направлены в другие стороны, это можно представить вращением (англ. rotate)
• если единицы измерения разные, например, метры в одной системе и километры в другой, это можно представить масштабированием (англ. scale)

Самый удивительный факт: любое элементарное трёхмерное преобразование, а также их комбинацию можно представить в виде матрицы 4×4! Чтобы понять, как это происходит, разберёмся с однородным представлением точек и векторов.

Единый тип данных для точек и векторов

Давайте представим, что нам поставили задачу: создать единый тип данных, способный хранить как трёхмерную точку, так и трёхмерный вектор. Этот тип данных должен поддерживать операции вращения, перемещения и масштабирования, причём по-разному для векторов и точек: например, перемещение вектора никак не меняет его, а перемещение точки изменяет эту точку.

Если использовать процедурную парадигму программирования, получится нечто такое:

Объектно-ориентированный подход предлагает такой вариант:

Оба подхода одинаково плохи: во-первых, мы в любом случае дублируем код. Во-вторых, на видеокартах с современной архитектурой любое ветвление или условное выполнение оборачивается огромным падением производительности, и желательно его избегать; в данных двух реализациях мы не сможем избежать ветвлений при выполнении трансформаций точек и векторов прямо на видеокарте.

Проблема решается с помощью математического приёма — однородного представления точек и векторов.

Однородное представление точек и векторов.

Давайте будем считать, что трёхмерная точка (x, y, z) хранится как четырёхкомпонентный вектор (x, y, z, 1) . А вектор хранится как (x, y, z, 0) . Всего лишь одно флаговое значение в конце позволяет избежать любых ветвлений в алгоритмах трансформации векторов и точек. Это происходит благодаря свойствам алгебры матриц.

Как известно, можно умножить матрицу на матрицу при условии, что ширина одной матрицы равна высоте другой (иначе операция просто недопустима). Для получения элемента с позицией i,j в новой матрице достаточно взять i-ю строку левой матрицы и j-й столбец правой матрицы. Вот пример:

Как ни странно, умножение 4-х компонентного вектора на матрицу 4×4 тоже возможно! Для этого достаточно считать 4-х компонентный вектор матрицей 4×1. После умножения получится новый 4-х компонентный вектор.

Ещё более удивительно, что любую комбинацию трёхмерных перемещений, поворотов, вращений (и не только их!) можно представить как всего лишь одну матрицу 4×4, называемую матрицей трёхмерной трансформации. При этом умножение матрицы на трёхмерную точки или вектор, записанный в однородном представлении, даёт новую точку или вектор именно так, как этого требуют правила преобразования точек и векторов. Никаких ветвлений, и никакой магии!

Класс CAnimatedCube

Давайте запомним несколько простых правил. Некоторые из них даже будут доказаны чуть ниже.

• умножение матрицы преобразования на вектор или точку в однородном представлении даёт преобразованный вектор или точку
• можно легко составить базовую матрицу, представляющих одно элементарное аффинное преобразование
• умножение матрицы A на матрицу B даёт новую матрицу, которая описывает новую трансформацию, созданную путём применения трансформации B, а затем A (именно в таком порядке)
• умножение матриц не коммутативно: вы не можете заменить A*B на B*A
• инвертирование матрицы (например, с помощью детерминанта матрицы) даёт матрицу обратной трансформации, которая вернёт точку или вектор в исходное состояние — в идеальном мире. В дискретном мире компьютеров обратное преобразование может быть чуть-чуть неточным из-за особенностей представления типов float и double.

Для демонстрации этих правил расширим класс CIdentityCube из предыдущего урока. Новый класс будет называться CAnimatedCube, и он будет демонстрировать работу трёх базовых аффинных трансформаций. Смена и продвижение анимации будет выполняться в методе Update, вызываемом периодически снаружи.

С учётом перечисленных выше правил, мы можем написать метод Draw для анимированного куба. При этом вместо glLoadMatixf следует применить glMultMatrixf, чтобы вместо замены уже существующей трансформации всего лишь модифицировать её. Если мы заменим матрицу GL_MODELVIEW, камера будет работать некорректно.

Функции для работы с аффинными трансформациями (и не только!) можно найти в GML:

Единичная матрица

Единичная матрица (матрица идентичности, англ. identity matrix) задает преобразование, при котором точки и векторы остаются без изменений, отображаясь сами в себя. Посмотрите сами на перемножение этой матрицы и точки/вектора:

Если мы не хотим возвращать из метода GetAnimationTransform() какую-либо преобразующую трансформацию, мы можем просто вернуть единичную матрицу. Именно такую матрицу создаёт конструктор по умолчанию класса glm::mat4. Теперь мы можем заложить каркас метода GetAnimationTransform:

Матрица перемещения

Матрица перемещения воздействует на точку, но вектор сохраняет неизменным. Действует она так:

В GLM есть функция glm::translate, умножающая переданную матрицу на матрицу перемещения. Чтобы анимировать куб, будем вычислять смещение по оси Ox в каждый момент времени. После этого получение матрицы перемещения будет очень простым:

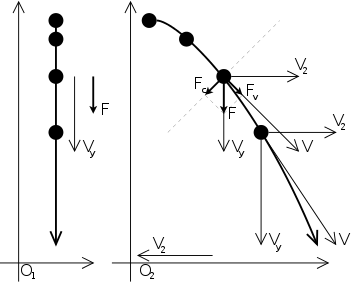
Для гладкого движения куба будем использовать прямолинейное равномерно ускоренное движение, аналогичное обычному прыжку или движению мача, брошенного вверх. Вот его иллюстрация в неинерциальной и инерциальной системах отсчёта:

В процессе анимации от 0% до 100% куб должен один или несколько раз прыгнуть в сторону и затем вернуться обратно. Для этого воспользуемся делением с остатком, а также формулой расчёта расстояния на основе начальной скорости и противоположно направленного ускорения. Можно написать так:

Матрица масштабирования

Матрица масштабирования воздействует как на точку, так и на вектор, изменяя соответственно удалённость точки от начала координат и длину вектора. Действует так:

В GLM есть функция glm::scale, умножающая переданную матрицу на матрицу масштабирования, имеющую потенциально разные коэффициенты масштабирования для трёх разных компонентов вектора.

Давайте используем эту функцию, чтобы реализовать пульсирование куба — сжатие от нормальных размеров к нулевым и обратно:

Матрица поворота

Матрица поворота воздействует и на точку, и на вектор, при этом удалённость точки от начала координат и длина вектора не меняются. Существует Теорема Эйлера, согласно которой любой поворот в трёхмерном пространстве вокруг произвольной оси можно представить как последовательность трёх поворотов вокруг трёх базовых осей системы координат в определённом порядке и на определённые углы:

Перечислим три матрицы поворота на угол “a” вокруг трёх осей системы координат (посмотреть, что получается при перемножении, вы можете самостоятельно):

В GLM есть функция glm::rotate, умножающая переданную матрицу на матрицу поворота вокруг переданного произвольного вектора оси на переданный угол. Как уже было сказано ранее, следует настроить GLM так, чтобы углы выдавались в радианах — иначе вы будете получать предупреждения об использовании устаревшего API. Проверьте, что в stdafx.h перед включением GLM объявлен макрос GLM_FORCE_RADIANS:

Матрицы поворота сложнее масштабирования или перемещения, но применить их для анимации проще: нужно всего лишь задать скорость поворота такой, чтобы за время анимации куб повернулся целое число раз:

Вот так это будет выглядеть к концу урока:

Как создать камеру

В OpenGL в режиме версии 1.x есть две трансформирующих вершины матрицы: GL_MODELVIEW и GL_PROJECTION. Матрица GL_MODELVIEW объединяет к себе как переход от локальной системы координат к мировой (Model), так и переход от мировых координат к системе коодинат камеры (View). Класс CCamera будет возвращать только одну компоненту GL_MODELVIEW: матрицу вида, созданную функцией glm::lookAt.

Правила движения камеры будут следующими:

• камера всегда смотрит на точку (0, 0, 0), вращается вокруг неё, приближается к ней или отдаляется
• для вращения камеры служат клавиши “Влево” и “Вправо” либо “A” и “D” на клавиатуре
• для приближения и отдаления служат клавиши “Вперёд” и “Назад” либо “W” и “S” на клавиатуре
• камера не может приближаться ближе чем на 1.5f и не может отдаляться дальше чем на 30.f
• камера не должна двигаться рывками, и даже при неравных интервалах перерисовки кадра движение должно оставаться плавным, т.е. зависит от deltaTime между кадрами

С учётом сказанного, спроектируем следующий интерфейс класса:

Методы Update, OnKeyDown, OnKeyUp должны вызываться извне — например, из класса окна. При этом методы обработки событий возвращают true, если событие было обработано, чтобы класс окна мог не рассылать это событие далее другим объектам.

Внутри класс хранит угол поворота камеры, отдаление от центра мира и подмножество клавиш, которые сейчас нажаты. Хранение подмножества нажатых клавиш позволяет легко устранить ряд непростых случаев:

• пользователь нажал “Влево”, затем “Вправо”, потом отпустил “Влево”; после этого камера должна вращаться вправо
• пользователь нажал “Влево” и “Вперёд”; после этого камера должна вращаться влево и при этом приближаться
• пользователь нажал “Вперёд” и “Назад”; при этом камера может не двигаться или двигаться в одном приоритетном направлении — оба варианта хороши

Чтобы отслеживать нажатие только нужных клавиш, создадим функцию-предикат ShouldTrackKeyPressed:

Также подключим заголовок с функциями вращения вектора, введём вспомогательные константы и функции, позволяющие получить скорость поворота и скорость приближения (возможно, нулевые или отрицательные) на основе информации о нажатых клавишах:

После этого с небольшим применением линейной алгебры мы можем реализовать методы класса CCamera:

Изменения в CWindow

Теперь класс CWindow должен хранить три объекта:

Конструктор CCamera требует два аргумента, их можно задать следующим образом:

CWindow::CWindow() : m_camera(CAMERA_INITIAL_ROTATION, CAMERA_INITIAL_DISTANCE)

В методе OnUpdateWindow мы должны вызывать метод Update у всех трёх объектов системы:

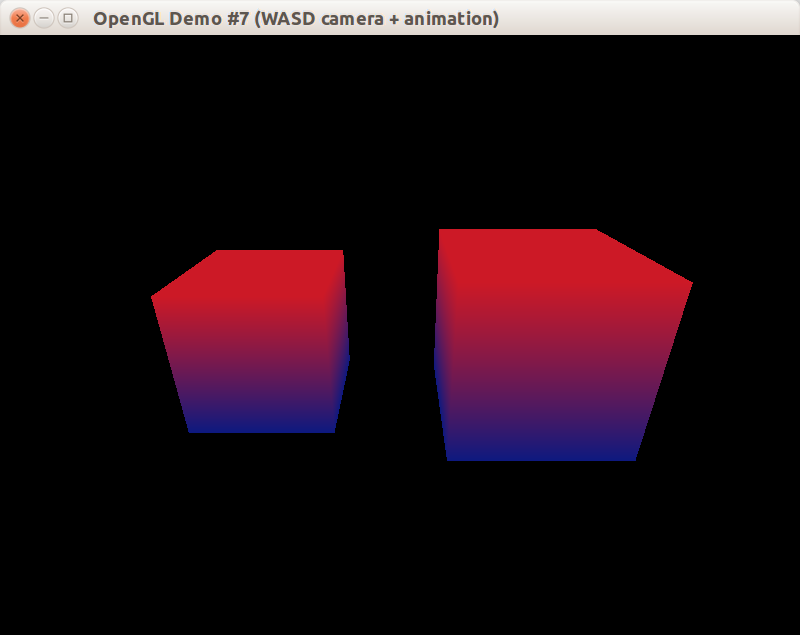
В методе Draw немного схитрим: применим вызов glTranslate (вместо нормальной работы с функциями GLM), чтобы развести два куба в стороны:

Метод SetupView станет проще, потому что мы можем не вычислять матрицу GL_MODELVIEW, а получить её начальное (для кадра) значение у камеры.

Наконец, следует перегрузить методы OnKeyDown/OnKeyUp класса CAbstractInputControlWindow в классе CWindow:

Конец!

Теперь вы можете взять полный пример (github.com) или посмотреть, каким будет результат запуска (в виде статичного скриншота):

Чтобы сделать результат более наглядным, была сделана серия скриншотов, которые затем были объединены в gif с помощью GIMP:

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.