Если диаметр окружности перпендикулярен хорде то он делит хорду пополам

Если диаметр делит хорду пополам, каково их взаимное расположение?

Если диаметр делит хорду пополам, то он перпендикулярен этой хорде.

Дано: окружность (O;R),

AB — диаметр, CD — хорда,

Соединим концы хорды CD с точкой O — центром окружности.

Так как OC=OD (как радиусы), то треугольник COD — равнобедренный с основанием CD.

Так как CP=PD, то OP — медиана треугольника COD, проведённая к основанию.

По свойству равнобедренного треугольника, OP является также его высотой.

Видео:Радиус перпендикулярный хорде делит ее пополамСкачать

Если диаметр окружности перпендикулярен хорде то он делит хорду пополам

ОКРУЖНОСТЬ И КРУГ. ЦИЛИНДР.

§ 70. ДИАМЕТР, ПЕРПЕНДИКУЛЯРНЫЙ К ХОРДЕ.

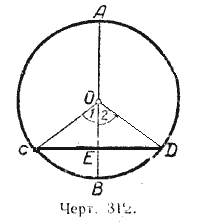
Теорема 1. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам.

Пусть диаметр АВ перпендикулярен к хорде СD (черт. 312). Требуется доказать, что
СЕ = ЕD, СВ = ВD, СА = DА.

Соединим точки С и D с центром окружности О. В равнобедренном треугольнике
СОD отрезок ЕО является высотой, проведённой из вершины О на основание СD; следовательно, ОЕ является и медианой и биссектрисой, т. е. СЕ = ЕD и / 1 = / 2. Но / 1 и / 2 суть центральные углы. Отсюда равны и соответствующие им дуги, а именно
СВ = ВD. Дуги СА и ВА также равны между собой, как дополняющие равные дуги до полуокружности.

Теорема 2 (обрaтная). Диаметр, проведённый через середину хорды, не проходящей через центр, перпендикулярен к ней и делит дуги, стягиваемые хордой, пополам.

Пусть диаметр АВ делит хорду СD пополам. Требуется доказать, что АВ_|_СD,
СВ = ВD и СА = АВ (черт. 313).

Соединим точки С и В с центром круга. Получим равнобедренный треугольник СОD, в котором ОК является медианой, а значит, и высотой. Следовательно, АВ_|_СD, а отсюда (по теореме 1) следует, что СА = АD; СВ = ВD .

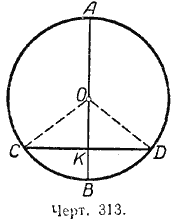
Теорема 3 (обратная).Диаметр, проведённый через середину дуги, делит пополам хорду, стягивающую эту дугу, и перпендикулярен к этой хорде.

Пусть диаметр АВ делит дугу СВD пополам (черт. 313). Требуется доказать, что
СК = КD и АВ _|_ СD.

Соединим центр круга О с точками С и D. В равнобедренном треугольнике СОD отрезок ОК является биссектрисой угла СОD, так как по условию теоремы СВ = ВD, поэтому ОК будет и медианой и высотой этого треугольника. Следовательно, диаметр АВ проходит через середину хорды и перпендикулярен к ней.

Видео:Теорема о диаметре, перпендикулярном хордеСкачать

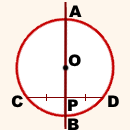
Диаметр, перпендикулярный хорде, делит ее пополам

Пусть АВ – хорда окружности, CD – перпендикулярный ей диаметр, пересекающий АВ в точке М. Треугольник ОАВ – равнобедренный, АО = ОВ как радиусы окружности. Тогда его высота ОМ является также и медианой, М – середина АВ.

1. Четырёхугольник АВСD вписан в окружность. Диаметр CC₁ перпендикулярен стороне AD и пересекает её в точке М, а диаметр DD₁ перпендикулярен стороне AB и пересекает её в точке N.

а) Пусть АА₁ также диаметр окружности. Докажите, что углы DNM и BA₁D₁ равны.

б) Найдите углы четырёхугольника ABCD, если угол CDB вдвое меньше угла ADB.

Диаметр, перпендикулярный хорде, делит ее пополам, поэтому N – середина АВ, М – середина АD.

Рассмотрим – средняя линия Значит, (накрест лежащие) – вписанные, опираются на одну дугу.

б) Найдем углы четырехугольника ABCD, если

Пусть тогда Треугольник – равнобедренный, поскольку медиана DN является его высотой. Значит, Тогда (из треугольника ).

– как центральный угол, опирающийся на ту же дугу.

Рассмотрим В этом треугольнике:

Тогда – по свойству четырехугольника, вписанного в окружность.

📺 Видео

Окружность, диаметр, хорда геометрия 7 классСкачать

Радиус и диаметрСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Радиус перпендикулярен хордеСкачать

Радиус перпендикулярный хорде делит ее пополамСкачать

Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Задача из советского КембриджаСкачать

Длина окружности. Математика 6 класс.Скачать

Геометрия Хорда AB окружности с центром O перпендикулярна радиусу OC и делит его пополам. НайдитеСкачать

ЗАДАЧА НА НАХОЖДЕНИЕ ДЛИНЫ ХОРДЫ, ПЕРПЕНДИКУЛЯРНОЙ ДИАМЕТРУ ОКРУЖНОСТИ. Задачи | ГЕОМЕТРИЯ 7 классСкачать

ОГЭ Задание 26 Свойство диаметра и хордыСкачать

Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Радиус перпендикулярен хордеСкачать

Геометрия. Свойства окружности. Диаметр и хордаСкачать

На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Радиус Хорда ДиаметрСкачать

ОГЭ Задание 25 Теорема Фалеса Свойство диаметра и хордыСкачать

[10] Окружности с нуля для ЕГЭ по математике. Линия центров перпендикулярна общей хорде и делит...Скачать