Если квадрат стороны треугольника больше

Теорема.

Если стороны прямоугольного треугольника измерены одной единицей, то квадрат числа, выражающего гипотенузу равен сумме квадратов чисел, выражающих катеты.

Эту теорему обыкновенно выражают сокращенно так:

Квадрат гипотенузы равен сумме квадратов катетов.

Это соотношение было впервые замечено греческим геометром Пифагором (VI в. до н.э.) и носит поэтому его имя — теорема Пифагора.

В треугольнике квадрат стороны, лежащей против острого угла, равен сумме квадратов двух других сторон без удвоенного произведения какой-нибудь из этих сторон на ее отрезок от вершины острого угла до высоты.

Пусть BС — сторона треугольника ABС (черт. 1 и черт. 2), лежащая против острого угла A , и BD — высота опущенная на какую-либо из остальных сторон, например, на AС (или на ее продолжение).Требуется доказать, что:

Из прямоугольных треугольников BDС и ABD выводим:

Подставив в равенство [1] вместо BD 2 и DС 2 их выражения из равенств [2] и [3] , получим:

Это равенство, после сокращения членов -AD 2 и +AD 2 , и есть то самое, которое требовалось доказать.

Замечание. Доказанная теорема остается верной и тогда, когда угол С прямой. Тогда отрезок СD обратится в ноль, т.е. AС станет равна AD, и мы будем иметь:

Что согласуется с теоремой о квадрате гипотенузы.

Теорема.

В треугольнике квадрат стороны, лежащей против тупого угла, равен сумме квадратов двух других сторон, сложенных с удвоенным произведением какой-нибудь из этих сторон на отрезок ее продолжения от вершины тупого угла до высоты. Доказательство аналогично предыдущему.

Следствие.

Из трех последних теорем выводим, что квадрат стороны треугольника равен, меньше или больше суммы квадратов других сторон, смотря по тому, будет ли противолежащий угол прямой, острый или тупой.

Отсюда следует обратное предложение: Угол треугольника окажется прямым, острым или тупым, смотря по тому, будет ли квадрат противолежащей стороны равен, меньше или больше суммы квадратов других сторон.

Видео:Решали пол-урока, а оказалось очень простоСкачать

Вычисление высоты треугольника по его сторонам.

Обозначим высоту, опущенную на сторону а треугольника ABС , через h_a. Чтобы вычислить ее, предварительно из уравнения:

находим отрезок основания с’:

.

После чего из DABD определяем высоту, как катет:

.

Таким же путем можно определить высоты h_b и h_с , опущенные на стороны b и с.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Вычисление медиан треугольника по его сторонам.

Пусть даны стороны треугольника ABС и требуется вычислить его медиану BD. Для этого продолжим ее на расстояние DE = BD и точку E соединим с A и С. Тогда получим параллелограмм ABCE.

Тогда .

Видео:Геометрия Докажите что если квадрат стороны треугольника равен неполному квадрату разности двухСкачать

Если квадрат стороны треуголника больше суммы квадратов двух других его сторон, то эта сторона лежит против : а)острого угла, б)прямого угла, в)тупого угла?

Геометрия | 5 — 9 классы

Если квадрат стороны треуголника больше суммы квадратов двух других его сторон, то эта сторона лежит против : а)острого угла, б)прямого угла, в)тупого угла.

a ^ 2 = b ^ 2 + c ^ 2 — 2 * a * b * cos(x).

A ^ 2 — (b ^ 2 + c ^ 2) = — 2 * a * b * cos(x) &gt ; 0 (условие задачи) , откуда cos(x)&lt ; 0 и x&gt ; 90 градусов.

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Верно ли это утверждение?

Верно ли это утверждение?

Точка, равноудаленная от сторон угла, лежит на биссектрисе этого угла.

Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Постройте треугольник по двум сторонам , прилежащему к ней углу и сумме двух других сторон?

Постройте треугольник по двум сторонам , прилежащему к ней углу и сумме двух других сторон.

Видео:РЕШЕНИЕ ТРЕУГОЛЬНИКОВ. Контрольная № 1 Геометрия 9 класс.Скачать

1) Внутри острого угла постройте квадрат со стороной, так чтоб две вершины лежали на одной стороне, а третья на другой стороне угла?

1) Внутри острого угла постройте квадрат со стороной, так чтоб две вершины лежали на одной стороне, а третья на другой стороне угла.

Видео:Почему в треугольнике против большей стороны - больший угол ➜ ДоказательствоСкачать

Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон то эта сторона лежит напротив 1) острого угла ; 2) прямого угла ; 3) тупого угла ; 4) нет правильного ответа?

Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон то эта сторона лежит напротив 1) острого угла ; 2) прямого угла ; 3) тупого угла ; 4) нет правильного ответа.

Видео:№157. В равнобедренном треугольнике основание больше боковой стороны на 2 см, но меньше суммы боковыСкачать

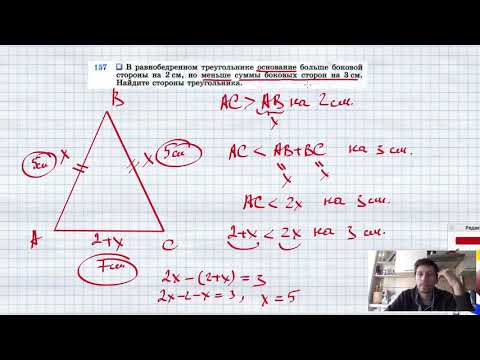
Внутри данного острого угла постройте квадрат с данной стороной так, чтобы две вершины квадрата принадлежали одной стороне угла, а третья — другой?

Внутри данного острого угла постройте квадрат с данной стороной так, чтобы две вершины квадрата принадлежали одной стороне угла, а третья — другой.

Видео:Теорема Пифагора для чайников)))Скачать

Квадрат со стороной а срезали по углам так, что получился правильный восьмиугольник?

Квадрат со стороной а срезали по углам так, что получился правильный восьмиугольник.

Найдите сторону восьмиугольника.

Видео:Разбор 31 варианта ОГЭ по математике 2024 / ПДФ решение + формулы / МатТаймСкачать

Найдите неизвестные стороны и углы треуголника, если сторона и два прилежащих к ней угла равны 8 ; 56 и 45 градусов Помогите, пожалуйста))?

Найдите неизвестные стороны и углы треуголника, если сторона и два прилежащих к ней угла равны 8 ; 56 и 45 градусов Помогите, пожалуйста)).

Видео:№206. Стороны треугольника равны 17 см, 15 см и 8 см. Через вершину A меньшего угла треугольника проСкачать

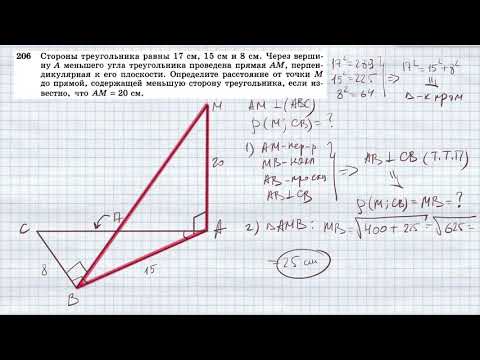
Утвержедние » квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними» называют 1) теорема синусов 2) теорема косинусов?

Утвержедние » квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними» называют 1) теорема синусов 2) теорема косинусов 3)теорема пифагора 4) теорема Фалеса ПОМОГИТЕ ПОЖАЛУЙСТА.

Видео:Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать

Утвержедние » квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними» называют 1) теорема синусов 2) теорема косинусов?

Утвержедние » квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними» называют 1) теорема синусов 2) теорема косинусов 3)теорема пифагора 4) теорема Фалеса срочно!

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Докажите, что в треугольнике : 1) против большей стороны лежит больший угол ; 2) обратно, против большего угла лежит большая сторона?

Докажите, что в треугольнике : 1) против большей стороны лежит больший угол ; 2) обратно, против большего угла лежит большая сторона.

На этой странице сайта вы найдете ответы на вопрос Если квадрат стороны треуголника больше суммы квадратов двух других его сторон, то эта сторона лежит против : а)острого угла, б)прямого угла, в)тупого угла?, относящийся к категории Геометрия. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

Видео:№156. Периметр треугольника ABC равен 15 см. Сторона ВС больше стороны АВ на 2 см, а сторона ABСкачать

Теорема Пифагора

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

• a = √c 2 − b 2
• b = √c 2 − a 2
• c = √a 2 + b 2

Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:

• если c 2 2 + b 2 , значит угол, противолежащий стороне c, является острым.
• если c 2 = a 2 + b 2 , значит угол, противолежащий стороне c, является прямым.
• если c 2 > a 2 +b 2 , значит угол, противолежащий стороне c, является тупым.

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a 2 + b 2 = c 2 .

Пошаговое доказательство:

• Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
• Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

• Также прямоугольная фигура ∆CBH подобна ∆ABC:

• Введем новые обозначения: BC = a, AC = b, AB = c.

• Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

• Значит a 2 = c * HB, b 2 = c * AH.
• Сложим полученные равенства:

a 2 + b 2 = c * HB + c * AH

a 2 + b 2 = c * (HB + AH)

a 2 + b 2 = c * AB

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

• Построим прямой угол с вершиной в точке C₁.
• Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

• Проведём отрезок A₁B₁.
• Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

• В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁ 2 = A₁C₁ 2 + B₁C₁ 2 .
• Таким образом получится:

• Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

1. C₁A₁ = CA и C₁B₁ = CB по результату построения,
2. A₁B₁ = AB по доказанному результату.

• Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
• Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Видео:Задача, которую боятсяСкачать

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?

Как решаем:

Пусть катеты a = 6 и b = 8.

По теореме Пифагора c 2 = a 2 + b 2 .

Подставим значения a и b в формулу:
c 2 = 6 2 + 8 2 = 36 + 64 = 100
c = √100 = 10.

Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?

• Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:

Ответ: треугольник не является прямоугольным.

🌟 Видео

Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

✓ Квадрат вписан в прямоугольный треугольник | Ботай со мной #129 | Борис ТрушинСкачать