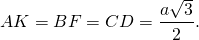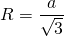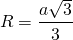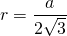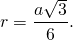Соотношения между сторонами и углами треугольника.
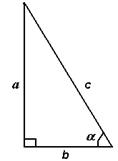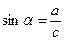 |  | В прямоугольном треугольнике синус угла равен отношению противолежащего катета к гипотенузе. |
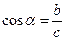 | В прямоугольном треугольнике косинус угла равен отношению прилежащего катета к гипотенузе. | |
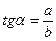 | В прямоугольном треугольнике тангенс угла равен отношению противолежащего катета к прилежащему. | |
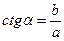 | В прямоугольном треугольнике котангенс угла равен отношению прилежащего катета к противолежащему. |
Теорема 24. (Пифагора) В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема 25. (Теорема, обратная теореме Пифагора) Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
С помощью теоремы, обратной к теореме Пифагора, можно по длинам сторон определить, является он прямоугольным или нет.
Наиболее интересны прямоугольные треугольники с целочисленными длинами сторон. Так, например, треугольники
3, 4, 5 и далее им подобные 6, 8, 10, далее 9, 12, 15 и т.д.
5, 12, 13 и далее им подобные 10, 24, 26 и т.д.
8, 15, 17 и далее им подобные.
7, 24, 25 и далее им подобные.
Скорее всего таких независимых серий прямоугольных треугольников с целочисленными длинами сторон бесконечно много.
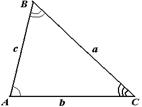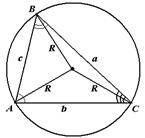  | Теорема 26. (синусов) Стороны треугольника пропорциональны синусам противолежащих углов. 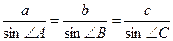 . Следствием к теореме синусов можно считать следующую теорему. Теорема 27. Стороны треугольника пропорциональны синусам противолежащих углов и их отношения равны двум радиусам описанной окружности около данного треугольника..  . |
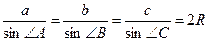| | Теорема 28. (косинусов) Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.  . |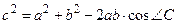
Дата добавления: 2014-12-22 ; просмотров: 7321 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Метрические соотношения в прямоугольном треугольнике. 1 часть. 9 класс.Скачать
Свойства равностороннего треугольника: теория и пример задачи
В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.
Видео:Математика | Метрические соотношения в прямоугольном треугольникеСкачать
Определение равностороннего треугольника
Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.
Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.
Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать
Свойства равностороннего треугольника
Свойство 1
В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.
Свойство 2
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.
CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.
Свойство 3
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.
Свойство 4
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.
Свойство 5
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r.
Свойство 6
В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:
1. Высоту/медиану/биссектрису:
2. Радиус вписанной окружности:
3. Радиус описанной окружности:
4. Периметр:
5. Площадь:
Видео:8 класс Геометрия. Метрические соотношения в прямоугольном треугольнике. Высота к гипотенузе Урок #7Скачать
Пример задачи
Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.
Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:
Видео:Как построить равнобедренный или равносторонний треугольник по клеткам.Скачать
Свойства равностороннего треугольника
Основные свойства равностороннего треугольника непосредственно следуют из свойств равнобедренного треугольника, частным случаем которого он является.
Свойства равностороннего треугольника
2) Высота, медиана и биссектриса, проведённые к каждой из сторон равностороннего треугольника, совпадают:
AK — высота, медиана и биссектриса, проведённые к стороне BC;
BF — высота, медиана и биссектриса, проведённые к стороне AC;
CD — высота, медиана и биссектриса, проведённые к стороне AB.
Длины всех трёх высот (медиан, биссектрис) равны между собой:
Если a — сторона треугольника, то
3) Точка пересечения высот, биссектрис и медиан называется центром правильного треугольника и является центром вписанной и описанной окружностей (то есть в равностороннем треугольнике центры вписанной и описанной окружностей совпадают).
4) Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, считая от вершин:
5) Расстояние от точки пересечения высот, биссектрис и медиан
до любой вершины треугольника равно радиусу описанной окружности:
6) Расстояние от точки пересечения высот, биссектрис и медиан до любой стороны треугольника равно радиусу вписанной окружности:
7) Сумма радиусов вписанной и описанной окружностей правильного треугольника равна его высоте, медиане и биссектрисе: R+r=BF.
8) Радиус вписанной в правильный треугольник окружности в два раза меньше радиуса описанной окружности:
💥 Видео
8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать
Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать
Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать
Соотношения между сторонами и углами треугольника. 7 класс.Скачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать
Геометрия, 9 класс | Метрические соотношения в окружностиСкачать
Математика, 10-й класс, Метрические соотношения в треугольнике. Теорема синусовСкачать
КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать
✓ Свойства и признаки равнобедренного треугольника | Ботай со мной #008 | Борис ТрушинСкачать
9 класс, 12 урок, Теорема о площади треугольникаСкачать
Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать
Геометрия Равносторонний треугольникСкачать
Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать
Урок 18. Соотношения между сторонами и углами треугольника (7 класс)Скачать
