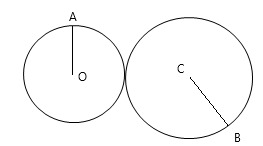
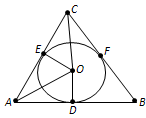
Вопросы по треугольникам и окружностям (8 видео)

Вопросы по треугольникам и окружностям

Прямые, содержащие катеты AC и CB прямоугольного треугольника АСВ, являются общими внутренними касательными к окружностям радиусов 2 и 4. Прямая, содержащая гипотенузу АВ, является их общей внешней касательной.

а) Докажите, что длина отрезка внутренней касательной, проведенной из вершины острого угла треугольника до одной из окружностей, равна половине периметра треугольника АСВ.

б) Найдите площадь треугольника АСВ.

а) Введём обозначения, как показано на рисунке, пусть M, H, N — точки касания. Касательные, проведённые к окружности из одной точки равны: AM = AN, CM = CH, HB = BN. Поэтому:

откуда p = AM, где Р — периметр, p — полупериметр треугольника.

б) Для определения площади треугольника используем формулу, связывающую её с полупериметром, стороной и радиусом вневписанной окружности, касающейся этой стороны и продолжений двух других сторон треугольника:

Ответ:

Примечание: указанная в решении формула легко может быть получена из следующих соображений где O₁ — центр окружности с радиусом r_1. При этом

Тогда

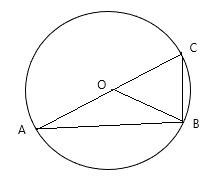
В остроугольном треугольнике ABC проведены высоты AP и CQ.

а) Докажите, что угол PAC равен углу PQC.

б) Найдите радиус окружности, описанной около треугольника ABC, если известно, что PQ = 8 и ∠ABC = 60°.

а) Углы APC и AQC — прямые, значит, точки A, Q, P и C лежат на одной окружности с диаметром AC, и, следовательно, равны и вписанные углы PAC и PQC этой окружности, опирающиеся на дугу PC, что и требовалось доказать.

б) Прямоугольные треугольники ABP и CBQ имеют общий угол ABC, следовательно, они подобны, откуда или но тогда и треугольники BAC и BPQ также подобны, причем коэффициент подобия равен откуда Тогда радиус R окружности, описанной около треугольника ABC равен

Ответ:

В остроугольном треугольнике KMN проведены высоты KB и NA.

а) Докажите, что угол ABK равен углу ANK.

б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и ∠KMN = 45°.

а) Углы NAK и NBK, опирающиеся на отрезок KN, равны, значит, точки A, B, N и K лежат на одной окружности, а, следовательно, равны и вписанные углы ABK и ANK этой окружности, опирающиеся на дугу AK, что и требовалось доказать.

б) Прямоугольные треугольники KMB и NMA имеют общий угол KMN, следовательно, они подобны, откуда или но тогда и треугольники KMN и BMA также подобны, причем коэффициент подобия равен откуда

Тогда радиус R окружности, описанной около треугольника ABM равен

Ответ:

Точка О — центр окружности, вписанной в треугольник ABC. На продолжении отрезка AO за точку О отмечена точка K так, что BK = OK.

а) Докажите, что четырехугольник ABKC вписанный.

б) Найдите длину отрезка AO, если известно, что радиусы вписанной и описанной окружностей треугольника ABC равны 3 и 12 соответственно, а OK = 5.

а) Пусть Так как — центр вписанной окружности треугольника ABC, то — биссектрисы углов и значит, Угол BOK внешний для треугольника AOB, поэтому (см. рисунок).

Так как (по построению), то тогда Углы CBK и KAC опираются на один и тот же отрезок CK и равны друг другу: Тогда по признаку, связанному со свойством вписанных углов, точки лежат на одной окружности.

б) Обозначим через радиусы вписанной и описанной окружностей треугольника Пусть H — проекция точки O на сторону AB (см. рис.), тогда Так как точки лежат на одной окружности, то радиус описанной окружности треугольника ABK совпадает с радиусом описанной окружности треугольника и равен Из треугольника ABK по теореме синусов: Тогда

Так как то

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Вопросы по треугольникам и окружностям

Тесты по геометрии 7 класс. Тема: «Окружность»

Правильный вариант ответа отмечен знаком +

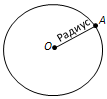
1. Радиусом окружности называется отрезок … Закончите определение:

— соединяющий две любые точки окружности

+ соединяющий центр окружности с какой-либо точкой окружности

— пересекающий окружность в двух точках

— ограничивающий дугу окружности

2. Окружность – это совокупность … точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки O, которая называется центром окружности. Вставьте пропущенное слово:

3. Часть плоскости, ограниченной окружностью, называется:

4. Центр окружности – это:

— точка, делящая радиус пополам

+ точка, равноудаленная от всех точек окружности

— точка, которая находится в пределах окружности

— точка, расположенная на диаметре окружности

5. Отрезок, проходящий через две точки и центр окружности, называется:

6. Как называется прямая, имеющая одну общую точку с окружностью?

7. Какой отрезок называется хордой?

+ соединяющий 2 точки окружности

— равный двум радиусам

— разделяющий окружность на 2 равные дуги

8. Дуга окружности – это:

+ часть окружности, ограниченная хордой

— множество равноудаленных от центра окружности точек

— две точки, соединенные отрезком

— часть окружности, равная радиусу

9. Диаметр, перпендикулярный хорде… Закончите утверждение:

+ делит эту хорду и дуги, которые она стягивает, пополам

— делится хордой пополам

— равен произведению длины радиуса и хорды

— называется секущей окружности

тест 10. Если 2 хорды равны, следовательно, они… Закончите утверждение:

— проходят через центр окружности

— выходят из одной точки окружности

— пересекают друг друга

+ стягивают 2 одинаковые дуги

11. Укажите формулу диаметра окружности D:

12. Две окружности пересекаются в одной точке. Радиус OA=20 см, радиус CB=30 см. Найдите расстояние между двумя центрами окружностей.

13. Дана окружность с центром O, в которую вписан треугольник ABC. Медиана треугольника OB=8 см. Чему равен диаметр окружности?

14. Дана окружность с центром О. Угол AOB=60 о , радиус OB=10 см. Найдите хорду AB.

15. Через три точки, которые не лежат на одной прямой… Закончите утверждение:

— можно провести три различных окружности

— можно провести равносторонний треугольник

+ можно провести только одну окружность

— нельзя построить параллельные прямые

16. Если две окружности соприкасаются в одной точке, то на какой прямой лежит эта точка?

+ на прямой, что проходит через центры окружностей

— на прямой, перпендикулярной радиусам окружностей

— на прямой, соединяющей центры вписанных в окружности треугольников

17. Как вычислить длину окружности через радиус?

18. Чему равно кратчайшее расстояние от центра окружности к касательной?

— квадратному корню из диаметра

— медиане вписанного треугольника

19. Секущая окружности – это:

— одна из сторон описанного треугольника

— прямая, параллельная диаметру окружности

— хорда, которая равна радиусу окружности

+ прямая, которая проходит через 2 точки окружности

тест-20. Если радиус окружности перпендикулярен к хорде, то он… Закончите утверждение:

— равен длине хорды

+ разделяет хорду пополам в точке их пересечения

— делит хорду в отношении 1:2

— делится пополам в точке пересечения с хордой

21. Что такое центральный угол окружности?

— угол, вершина которого лежит на окружности, а стороны угла пересекают окружность

— угол, равный 60 0

+ угол, вершиной которого является центр окружности

— угол, одна из сторон которого проходит через центр окружности

22. Если вписанный угол равен 90 0 , то он… Закончите утверждение:

+ опирается на диаметр

— имеет равные стороны

— имеет сторону, проходящую через центр окружности

— имеет сторону, равную радиусу

23. Как называется часть окружности, которая соединяет 2 точки на окружности?

24. Как измеряется вписанный угол?

— равен дуге, на которую он опирается

— равен центральному углу, опирающемуся на ту же дугу

+ равен половине дуги, на которую он опирается

25. Если вписанные углы опираются на одну дугу, то они… Закончите утверждение:

+ равны между собой

26. Дана окружность с центром O. AB – касательная к окружности. Угол ABO=33 0 , чему равен угол BOA?

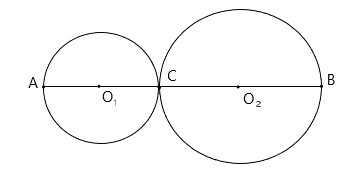
27. Даны две окружности с центрами O₂ и O₁, которые касаются в точке C. Радиус меньшей окружности равен 4 см, длина отрезка AB=20 см. Чему равен радиус большей окружности?

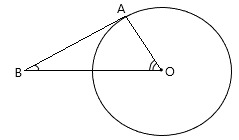
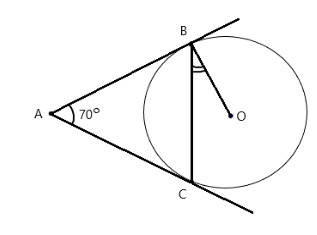
28. Лучи AB и AC касаются окружности с центром О в точках B и C. Угол BAC=70 0 . Найдите угол OBC.

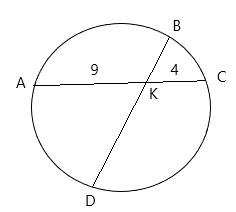
29. Найдите длину хорды BD, если AK=9 см, KC=4 см, BK:KD = 1:4.

тест_30. A – точка касания окружности с центром O и прямой AB. OA=9 см, AB=12 см. Найдите длину отрезка CB.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Вопросы по треугольникам и окружностям

Вопрос 1. Что такое окружность, центр окружности, радиус?
Ответ. Окружностью называется фигура, которая состоит из всех точек плоскости, равноудалённых от данной точки. Эта точка называется центром окружности.
Расстояние от точек окружности до её центра называется радиусом. Радиусом называется также любой отрезок, соединяющий точку окружности с её центром.

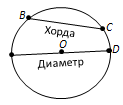
Вопрос 2. Что такое хорда окружности? Какая хорда называется диаметром?
Ответ. Отрезок, соединяющий две точки окружности, называется хордой. Хорда проходящая через центр, называется диаметром.

Вопрос 3. Какая окружность называется описанной около треугольника?
Ответ. Окружность называется описанной около треугольника, если она проходит через все его вершины.

Вопрос 4. Докажите, что центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам треугольника.
Ответ. Теорема 5.1. Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведённых через середины этих сторон.
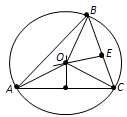
Доказательство. Пусть ABC – данный треугольник и O – центр описанной около него окружности (рис. 93). Треугольник AOC равнобедренный: у него стороны OA и OC равны как радиусы. Медиана OD этого треугольника одновременно является его высотой. Поэтому центр окружности лежит на прямой, перпендикулярной стороне AC и проходящей через её середину. Точно так же доказывается, что центр окружности лежит на перпендикулярах к двум другим сторонам треугольника. Теорема доказана.

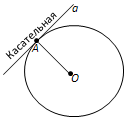
Вопрос 5. Какая прямая называется касательной к окружности?
Ответ. Прямая, проходящая через точку окружности перпендикулярно к радиусу, проведённому в эту точку, называется касательной. При этом данная точка окружности называется точкой касания.

Вопрос 6. Что значит: окружности касаются в данной точке?
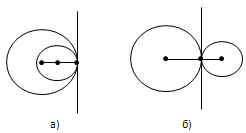
Ответ. Говорят, что две окружности, имеющие общую точку, касаются в этой точке, если они имеют в этой точке общую касательную (рис. 97).

Вопрос 7. Какое касание окружностей называется внешним, какое – внутренним?
Ответ. Касание окружностей называется внутренним, если центры окружностей лежат по одну сторону от их общей касательной (рис. 97, а). Касание окружностей называется внешним, если центры окружностей лежат по разные стороны от их общей касательной (рис. 97, б).

Вопрос 8. Какая окружность называется вписанной в треугольник?
Ответ. Окружность называется вписанной в треугольник, если она касается всех его сторон.

Вопрос 9. Докажите, что центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.
Ответ. Теорема 5.2. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Доказательство. Пусть ABC – данный треугольник, O – центр вписанной в него окружности, D, E и F – точки касания окружности со сторонами (рис. 98). Прямоугольные треугольники AOD и AOE равны по гипотенузе и катету. У них гипотенуза AO общая, а катеты OD и OE равны как радиусы. Из равенства треугольников следует равенство углов OAD и OAE. А это значит, что точка O лежит на биссектрисе треугольника, проведённой из вершины A. Точно так же доказывается, что точка O лежит на двух других биссектрисах треугольника. Теорема доказана.

Вопрос 10. Объясните, как построить треугольник по трём сторонам.
Ответ. Задача 5.1. Построить треугольник с данными сторонами a, b, c (рис. 99, а).
Решение. С помощью линейки проводим произвольную прямую и отмечаем на ней произвольную точку B (рис. 99, б). Раствором циркуля, равным a, описываем окружность с центром B и радиусом a. Пусть C – точка её пересечения с прямой. Теперь раствором циркуля, равным c, описываем окружность из центра B, а раствором циркуля, равным b, описываем окружность из центра C. Пусть A – точка пересечения этих окружностей. Проведём отрезки AB и AC. Треугольник ABC имеет стороны, равные a, b, c. Что и требовалось оъяснить.