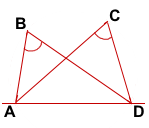
Признак принадлежности четырёх точек одной окружности
Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.
Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,
Доказать: точки A, B, C, D лежат на одной окружности
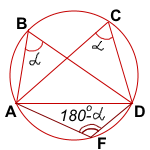
Опишем около треугольника ABD окружность.
Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.
Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:
Рассмотрим четырехугольник ACDF.
Отсюда следует, что четырёхугольник ABDF — вписанный.
Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.
Видео:Как искать точки на тригонометрической окружности.Скачать

Точка внутри и вне окружности
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом занятии мы изучим тему «Точка внутри и вне окружности». На этом итоговом уроке мы повторим понятие окружности, вспомним ее основные свойства. Рассмотрим примеры расположения точки внутри и вне окружности. Вместе с преподавателем решим несколько задач на эту тему.
Видео:Определение принадлежности точки окружностиСкачать

Как определить лежит ли точка на окружности
Вводятся координаты (x;y) точки и радиус круга ( r ). Определить принадлежит ли данная точка кругу, если его центр находится в начале координат.
Будем считать, что точка принадлежит кругу, если находится внутри его или на его окружности.
Из любой точки координатной плоскости можно провести отрезок к началу координат. Если длина этого отрезка больше радиуса круга, то точка лежит за пределами круга и, следовательно, не принадлежит ему. Если же отрезок, соединяющий точку и начало координат, меньше радиуса круга с центром в начале координат или равен ему, то точка будет принадлежать кругу.
Отрезок между любой точкой и нулевой точкой (началом координат) является гипотенузой прямоугольного треугольника, катеты которого равны значениям x и y координаты данной точки.
Таким образом задача сводится по-сути к двум действия:
- Нахождение длины отрезка между точкой и началом координат по теореме Пифагора (квадрат длины гипотенузы равен сумме квадратов длин катетов).
- Сравнению полученного значения с радиусом круга.
Задача
Даны координаты точки и радиус круга с центром в начале координат. Определить, принадлежит ли данная точка кругу.
Решение
- x, y, r – координаты точки и радиус круга;
- r_xy – длина гипотенузы (расстояния от начала координат до точки).
Алгоритм решения задачи:
Следует рассмотреть прямоугольный треугольник, один катет которого лежит на любой оси, а другой является перпендикуляром к этой оси из заданной точки. В этом случае длины катетов равны значениям x и y, а гипотенуза является отрезком, соединяющим начало координат с точкой. Если этот отрезок не больше радиуса круга, то делается вывод, что точка принадлежит кругу.
Длина гипотенузы находится по теореме Пифагора.
Определить, принадлежит ли точка с координатами (x; y) кругу радиуса R с центром в начале координат.
Пользователь вводит координаты точки и радиус круга.
Если выбрать точку на координатной плоскости, то можно увидеть, что проекции ее координат на оси x и y являются катетами прямоугольного треугольника. А гипотенуза этого прямоугольного треугольника как раз показывает расстояние от начала координат до точки. Таким образом, если длина гипотенузы будет меньше радиуса круга, то точка будет принадлежать кругу; иначе она будет находится за его пределами.
Длину гипотенузы можно вычислить по теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Пример выполнения программы:
Обратите внимание, можно вводить отрицательные координаты. При возведении в квадрат все-равно будет получено положительное число.
📽️ Видео
Всё про углы в окружности. Геометрия | МатематикаСкачать

№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

10 класс, 11 урок, Числовая окружностьСкачать

Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

5 класс, 22 урок, Окружность и кругСкачать

Окружность. 7 класс.Скачать

Бондарев А.А. - 5. Доклад "О некоторых классах обеспечения неустойчивости"Скачать

Точки на числовой окружностиСкачать

Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

"Парадоксальное" среднее расстояние между точками на окружностиСкачать

Попадание точки в заданную область. Два сектора. Уроки программирования на С++.Скачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Найти часть медианы треугольника, если некоторые его точки лежат на окружностиСкачать

Уравнение окружности (1)Скачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

2020 точка О центр окружности на которой лежат точки A B и C известно что Угол ABC равен 62 градусаСкачать

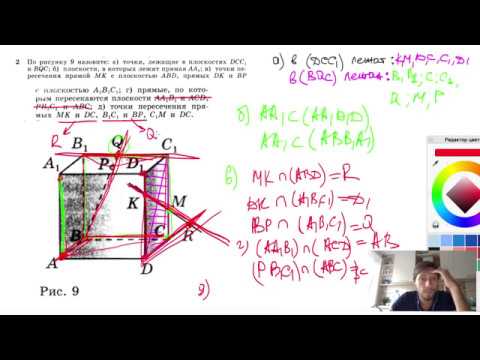
№2. По рисунку 9 назовите: а) точки, лежащие в плоскостях DCC1 и BQCСкачать
ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать