Укажите параллелограммы докажите что все указанные вами четырехугольники параллелограммы

Как доказать, что четырехугольник — параллелограмм? Для этого можно использовать определение либо один из признаков параллелограмма.

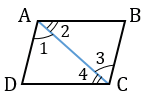
1) Четырехугольник является параллелограммом по определению, если у него противолежащие стороны параллельны, то есть лежат на параллельных прямых.

ABCD — параллелограмм, если

Для доказательства параллельности прямых используют один из признаков параллельности прямых, чаще всего — через внутренние накрест лежащие углы. Для доказательства равенства внутренних накрест лежащих углов можно доказать равенство пары треугольников.

Например, это могут быть пары треугольников

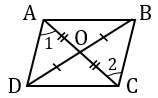
2) Четырехугольник является параллелограммом, если у него диагонали в точке пересечения делятся пополам.

Чтобы использовать этот признак параллелограмма, надо сначала доказать, что AO=OC, BO=OD.

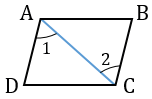
3) Четырехугольник является параллелограммом, если у него противолежащие стороны параллельны и равны.

Чтобы использовать этот признак параллелограмма, надо сначала доказать, что AD=BC и AD ∥ BC (либо AB=CD и AB ∥ CD).

Для этого можно доказать равенство одной из тех же пар треугольников.

Чтобы воспользоваться этим признаком параллелограмма, нужно предварительно доказать, что AD=BC и AB=CD.

Для этого доказываем равенство треугольников ABC и CDA или BCD и DAB.

Это — четыре основных способа доказательства того, что некоторый четырехугольник — параллелограмм. Существуют и другие способы доказательства. Например, четырехугольник — параллелограмм, если сумма квадратов его диагоналей равна сумме квадрату сторон. Но, чтобы воспользоваться дополнительными признаками, надо их сначала доказать.

Доказательство с помощью векторов или координат также опирается на определение и признаки параллелограмма, но проводится иначе. Об этом речь будет вестись в темах, посвященных векторам и декартовым координатам.

Видео:8 класс, 4 урок, ПараллелограммСкачать

Признаки параллелограмма

Доказательство:

Дано: АВСD — четырехугольник, АD = ВС, АDВС.

Доказать: АВСD — параллелограмм.

Доказательство:

1. Проведем диагональ АС четырехугольника АВСD.

2. Рассмотрим АВС и АDС: АС — общая, 1 =3 (т.к. по условию АDВС, 1 и 3 накрест лежащие углы при пересечении параллельных прямых АD и BC секущей АС), АВС =АDС (по 1 признаку равенства треугольников), АВ = DC и 2 = 4. Но 2 и 4 накрест лежащие углы при пересечении прямых АВ и DС секущей АС, АВDС.

3. Итак, АDВС и АВDС, т.е. в четырехугольнике АВСD противоположные стороны попарно параллельны, четырехугольник АВСD — параллелограмм. Что и требовалось доказать.

Доказательство:

Дано: АВСD — четырехугольник, АВ = DС, АD = ВC.

Доказать: АВСD — параллелограмм.

Доказательство:

1. Проведем диагональ АС четырехугольника АВСD.

2. Рассмотрим АВС и АDС: АС — общая, по условию АВ = DС, АD = ВC, АВС =АDС (по 3 признаку равенства треугольников), 1 = 2, при этом 1 и 2 накрест лежащие при пересечении прямых АD и ВC секущей АС, по признаку параллельности двух прямых АDВС.

3. Итак, АD = ВC, АDВС, по 1 0 признаку параллелограмма, четырехугольник АВСD — параллелограмм. Что и требовалось доказать.

Доказательство:

Дано: АВСD — четырехугольник, АС и DВ диагонали, АС ∩ DВ = О, АО = ОС, DО = ОВ.

Доказать: АВСD — параллелограмм.

Доказательство:

1. Рассмотрим АОD и ВОС: по условию АО = ОС, DО = ОВ, АОD и ВОС (как вертикальные углы), АОD =ВОС (по 1 признаку равенства треугольников), АD = ВC и 1 = 2.

2. 1 и 2 накрест лежащие при пересечении прямых АD и ВC секущей АС, при этом 1 = 2, по признаку параллельности двух прямых АDВС.

3. Итак, АD = ВC, АDВС, по 1 0 признаку параллелограмма, четырехугольник АВСD — параллелограмм. Что и требовалось доказать.

Поделись с друзьями в социальных сетях:

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Работа №1.2. Параллелограмм. Лысенко Ф.Ф.

Работа №1.2. Параллелограмм. Лысенко Ф.Ф.

Вариант 1.

1. Продолжите предложения.

а) Параллелограммом называют ___________________ , у которого противоположные стороны ______________________ .

б) В параллелограмме противоположные углы _____________________ , сумма соседних углов ____________________________ .

2. Нарисуйте 2 различных параллелограмма и отметьте в каждом из них

а) равные углы и равные стороны;

б) равные отрезки диагоналей.

3. ABCD — параллелограмм. ВС = 5 см, CD = 3 см, ∠А = 46º. Запишите величины:

Периметр параллелограмма = _______ см.

4. MPKT — параллелограмм. O — точка пересечения диагоналей. РТ = 5, РК = 3, МО=4. Запишите величины:

= _______ см.

5. В параллелограмме ABCD проведена биссектриса АК. AD = 7 см, CD = 6 см, АК = 5 см. Найдите периметр ADCK.

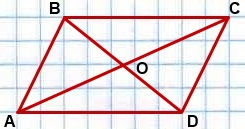
6. Используя данные рисунка 6,

а) укажите параллелограммы ______________________ ;

б) докажите, что все указанные вами четырёхугольники — параллелограммы.

🎬 Видео

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Признаки параллелограмма Доказательство признаков параллелограммаСкачать

№378. Докажите, что параллелограмм является выпуклым четырехугольником.Скачать

Параллелограмм. Практическая часть - решение задачи. 8 класс.Скачать

Параллелограмм. Практическая часть - решение задачи. 8 класс.Скачать

№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать

№429. Докажите, что выпуклый четырехугольник является параллелограммом, если сумма углов, прилежащихСкачать

Признаки параллелограмма. 8 класс.Скачать

8 класс, 5 урок, Признаки параллелограммаСкачать

Геометрия Четырехугольник ABCD и AMKD – параллелограммы (см. рис.). Докажите, что четырехугольникСкачать

Параллелограмм. 8 класс.Скачать

Геометрия 8 класс. Параллелограмм, свойства параллелограммаСкачать

Свойства параллелограмма. 8 класс.Скачать

№383 На диагонали BD параллелограмма ABCD отмечены две точки Р и Q так, что PB=QD. ДокажитеСкачать

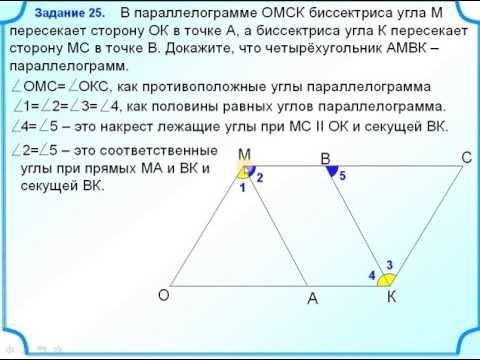
Задание 25 Доказать, что четырёхугольник параллелограмм Определение параллелограммаСкачать

Четырехугольники. Две задачи с параллелограммом. Математика 8 класс.Скачать

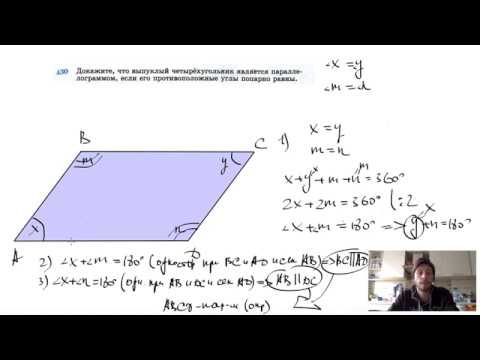
№430. Докажите, что выпуклый четырехугольник является параллелограммом, если его противоположныеСкачать

Четырехугольники. Геометрия 8 класс.Скачать