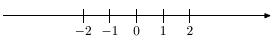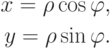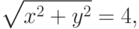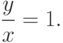Координаты и векторы краткий конспект (4 видео)

Векторы: основные определения и понятия

Скалярная величина — величина, которая может быть охарактеризована числом. Например, длина, площадь, масса, температура и т.д.

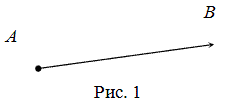
Вектором называется направленный отрезок $overline$; точка $A$ — начало, точка $B$ — конец вектора (рис. 1).

Вектор обозначается либо двумя большими буквами — своим началом и концом: $overline $ либо одной малой буквой: $overline$.

Если начало и конец вектора совпадают, то такой вектор называется нулевым. Чаще всего нулевой вектор обозначается как $overline$.

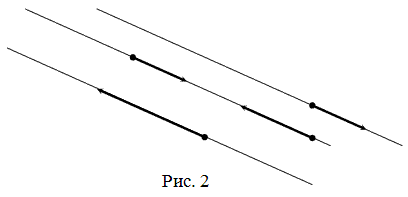
Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых (рис. 2).

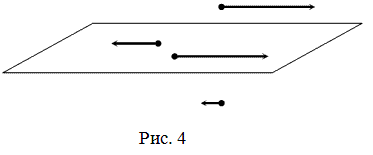
Векторы называются компланарными, если они параллельны одной плоскости или лежат в одной плоскости (рис. 4).

Два вектора всегда компланарны.

Длиной (модулем) вектора $overline $ называется расстояние между его началом и концом: $|overline |$

Подробная теория про длину вектора по ссылке.

Длина нулевого вектора равна нулю.

Вектор, длина которого равна единице, называется единичным вектором или ортом.

Векторы называются равными, если они лежат на одной или параллельных прямых; их направления совпадают и длины равны.

Иначе говоря, два вектора равны, если они коллинеарны, сонаправлены и имеют равные длины:

В произвольной точке $M$ пространства можно построить единственный вектор $overline$, равный заданному вектору $overline $.

Содержание

Координаты и векторы
Координаты и векторы
Геометрия. 11 класс
📹 Видео

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Координаты и векторы

Числовой осью называется бесконечная прямая, на которой определены: точка O — начало отсчета; положительное направление, указываемое стрелкой; масштаб измерения (принцип отложения чисел на оси, часто с указанием единицы измерения). Условное изображение числовой прямой (числового луча) приведено на рис. 3.1.

Для каждого действительного числа x на числовой оси R определена единственная точка, соответствующая его количеству (изображающая это число с учетом выбранного масштаба и отсчета) и наоборот, то есть совокупность R и множество точек числовой оси могут быть связаны общим, однозначно определяемым правилом, законом.

Пример. Числу 5 на числовой оси соответствует точка, удаленная на расстояние в 5 единиц масштаба от начальной точки (точки отсчета 0 ).

Пример. Точке A , удаленной на расстояние 3 единицы масштаба от начала координат O можно сопоставить число 3.

Числовая прямая, расположенная обычно на плоскости горизонтально к рассматривающему, называется осью x ( Ox ), а числовая прямая, расположенная обычно вертикально к нему, — осью y (Oy) .Эти прямые образуют систему ориентации каждой точки на плоскости по двум ее координатам.

Плоскость, определяемая этими двумя перпендикулярными (или, как говорят в математике, ортогональными) числовыми прямыми, называется плоскостью xy (xOy) .

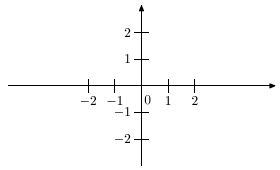
Каждая пара вещественных значений (x;y) задает одну единственную точку M(x;y) на этой плоскости, которая определяется как точка пересечения перпендикулярных (ортогональных) прямых, проходящих через значения x оси Ox и значение y оси Oy . Наоборот, каждой точке (x;y) можно сопоставить пару вещественных чисел: x — на оси Ox и y — на оси Oy . Так определенная система двух перпендикулярных числовых прямых называется прямоугольной декартовой системой координат на плоскости (рис. 3.2).

Оси координат обычно помечаются буквами.

Ось Ox называется осью абсцисс , ось Oy — осью ординат .Эти оси делят плоскость xOy на 4 части (координатных угла или, как их еще называют, квадранта).

Упорядоченная система трех взаимно перпендикулярных осей с общим началом отсчета (началом координат) и общей единицей измерения длины (масштабом) называется прямоугольной декартовой системой координат в пространстве .Обозначается такая система Oxyz или xyz . Ось Ox называется осью абсцисс , Oy — осью ординат , Oz — осью аппликат .

Кроме декартовой системы координат, часто используют и другие удобные, не обязательно прямоугольные, системы координат.

Одной из наиболее часто используемых является полярная система координат , определяющая, как и в декартовой системе, однозначное положение точки на плоскости с помощью двух параметров.

Возьмем на плоскости точку O (называемую полюсом ) и выходящую из этой точки полупрямую (называемую полярной осью ). Если на этой прямой задать масштаб и положительное направление, то мы определим полярную систему координат. Положение точки M на плоскости в полярной системе координат задается двумя числовыми величинами: — расстоянием точки M от полюса, то есть и — углом, образованным отрезком OM с положительным направлением полярной оси. Обозначим точку с полярными координатами в виде . Обычно считают, что , 0″ style=»display: inline; «>. Эти значения называются главными значениями. Каждая точка на плоскости однозначно определяется полярными координатами. Исключение составляет единственная точка , где угол может быть любым. Условно, в этом случае берется угол .

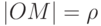
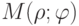
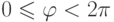
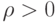
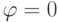
Найдем зависимость между координатами точки M(x;y) в прямоугольной декартовой системе координат и ее координатами 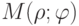в полярной системе.

Построим прямоугольную систему xOy , где ось Ox совпадает с полярной осью, O(0;0) — начала координат, а положительные направления этих осей совпадают (рис. 3.3).

Используя прямоугольные треугольники и тригонометрические функции, получим следующие основные соотношения:

Таким образом, зная полярные координаты точки, можно найти прямоугольные координаты этой же точки. Кроме того, если использовать основное тригонометрическое соотношение и определение тангенса угла из школьного курса (нужно сложить квадраты x , y , а затем поделить y на x ), то справедливы следующие соотношения:

Пример. Если , , то по соответствующим формулам получаем

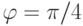
Пример. Уравнение окружности с центром в начале координат и радиуса r в декартовой системе координат, как известно, имеет вид: x 2 +y 2 =r 2 . Уравнение окружности в полярных координатах будет иметь вид

Удобной в пространстве системой координат является и так называемая сферическая система координат . В этой системе положение точки M(x;y;z) в пространстве однозначно определяется ее расстоянием r от начала координат (длиной отрезка OM ), углом между OM и положительной полуосью Oz и углом ( между проекцией OM на плоскость xOy и положительной полуосью Ox (рис. 3.4).

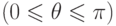
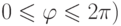
Выясним форму связи сферических и декартовых координат. По рис. 3.4:

Видео:9 класс, 2 урок, Координаты вектораСкачать

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Урок № 1. Координаты в пространстве. Система координат

Перечень вопросов, рассматриваемых в теме:

Прямоугольная система координат в пространстве.
Координаты вектора, радиус-вектор.
Координаты середины отрезка, длина вектора, расстояние между точками.

Гусева В.А., Куланин Е.Д. Геометрия. Профильный уровень. 10 класс — М.: Бином, 2010 — с. 130-148

Погорелов А.В. Геометрия. Учеб. для 7-11 кл. общеобразоват. Учреждение — 13-е изд-е. — М.: Просвещение, 2014. — с. 51-52

Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7-9 кл. 20-е изд-е. — М.: Просвещение, 2010. — с. 259-270.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч отрицательной полуосью. Плоскости, проходящие соответственно через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями и обозначаются Оху, Оуz, Оzх.

Прямоугольная система координат в пространстве задана, если выбрана точка – начало координат, через эту точку проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление (оно обозначается стрелкой) и задана единица измерения отрезков (рис. 121). Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат.

Зададим в пространстве прямоугольную систему координат Охуz. На каждой из положительных полуосей отложим от начала координат единичный вектор, т. е. вектор, длина которого равна единице. Обозначим через единичный вектор оси абсцисс, через – единичный вектор оси ординат и через – единичный вектор оси аппликат (рис. 124). Векторы , , – назовем координатными векторами. Очевидно, эти векторы не компланарны. Поэтому любой вектор a и можно разложить по координатным векторам, т. е. представить в виде

причем коэффициенты разложения х, у, z определяются единственным образом.

Коэффициенты х, у и z в разложении вектора по координатным векторам называются координатами вектора в данной системе координат. Координаты вектора будем записывать в фигурных скобках после обозначения вектора: .

Нулевой вектор можно представить в виде так как все координаты нулевого вектора равны нулю.

Так как нулевой вектор можно представить в виде то все координаты нулевого вектора равны нулю. Далее, координаты равных векторов соответственно равны, т. е. если векторы <х₁, y₁, z₁> и <х_2, y₂, z₂) равны, то х₁ = x₂, y₁ = y₂ и z₁ = z₂

Рассмотрим правила, которые позволяют по координатам данных векторов найти координаты их суммы и разности, а также координаты произведения данного вектора на данное число.

1)Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Другими словами, если <х₁, у₁, z₁> и <х₂, у₂, z₂> — – данные векторы, то вектор + имеет координаты <х₁+х₂, у₁ + у₂, z₁ + z₂>.

2)Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Другими словами, если <х₁, y₁, z_1> и b<х₂ у₂; z₂> – данные векторы, то вектор – имеет координаты <х₁ – х₂, y₁ – y₂, z₁ – z₂>.

3)Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. Другими словами, если – данный вектор, α – данное число, то вектор α имеет координаты <αх; αу; αz).

1)Признак коллинеарности векторов: Для того, чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы один из них был произведением другого на некоторое число.

Следствие: ненулевой вектор коллинарен вектору тогда и только тогда, когда существует такое число α, что =α .

Определение: Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.

2)Признак компланарности трех векторов: если вектор можно разложить по векторам и , т. е. представить в виде = x + y , где x и y — – некоторые числа, то векторы , и компланарны.

Определение: Вектор, конец которого совпадает с данной точкой, а начало — с началом координат, называется радиус-вектором данной точки.

Каждая координата вектора равна разности соответствующих координат его конца и начала.

Каждая координата середины отрезка равна полусумме соответствующих координат его концов.

Длина вектора вычисляется по формуле: