Задание 26. Четырёхугольник ABCD со сторонами АВ=11 и CD = 41 вписан в окружность. Диагонали АС и BD пересекаются в точке К, причём угол AKB = 60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Углы 

Четырехугольник DNAB вписан в окружность, следовательно,
Далее, 
Рассмотрим треугольник NAB вписанный в окружность. По теореме косинусов, имеем:
По теореме синусов можно записать:

где R – радиус описанной окружности. Из последнего выражения:
Видео:Четырехугольник АВСD со сторонами АВ=12 иСD=13 вписан в окружность. 27 вариант Ященко ОГЭ задача 25Скачать

Решение №2427 Четырёхугольник ABCD со сторонами АВ = 40 и CD = 10 вписан в окружность.
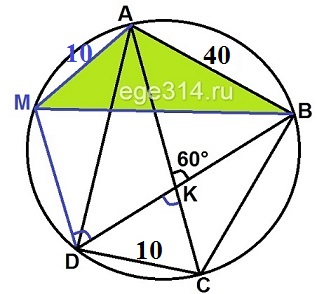
Четырёхугольник ABCD со сторонами АВ = 40 и CD = 10 вписан в окружность. Диагонали АС и BD пересекаются в точке K, причём ∠AKB = 60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Источник: ОГЭ Ященко 2022 (36 вар)
Проведём прямую DM параллельную АС. Дуги ‿АМ = ‿DC, значит и хорды равны DC = AM = 10.
∠ABK = ∠DKC = 60°, как вертикальные. ∠MDK = ∠DKC = 60°, как накрест лежащие углы, при AC||MD и секущей DK.
Четырёхугольник AMDB вписан в окружность, сумма противоположных углов равна 180°. Найдём ∠MAB:
∠MAB = 180° – ∠MDB = 180° – 60° = 120°
По теореме косинусов найдём MB:
MB 2 = AM 2 + AB 2 – 2·AM·AB·cos 120°
Найдём радиус описанной вокруг ΔABM окружности по теореме синусов:
Ответ: .
Видео:Геометрия Четырёхугольник ABCD со сторонами AB = 2 и CD = 5 вписан в окружность. Диагонали AC и BDСкачать

Задачи №26 на ГИА по математике
материал для подготовки к егэ (гиа) по геометрии (9 класс) на тему
В работе представлена подборка из 40 задач по геометрии повышенного уровня сложности из Открытого Банка заданий ГИ А с подробными решениями и хорошими чертежами. Материал может быть полезен как для учителей математики так и для учащихся.
Видео:Четырёхугольник ABCD со сторонами AB = 40 и CD = 10 вписан в окружность. Диагонали #огэ #математикаСкачать

Скачать:
| Вложение | Размер |
|---|---|
| zadachi_no_26_na_gia_po_matematike.docx | 306.8 КБ |
Видео:Задание 16 (В1) ОГЭ по математике ▶ №11 (Минутка ОГЭ)Скачать

Предварительный просмотр:
- Задание №361445 стр.32
Четырёхугольник ABCD со сторонами AB =25 и CD =16 вписан в окружность. Диагонали AC и BD пересекаются в точке K , причём ∠ AKB =60 ∘ . Найдите радиус окружности, описанной около этого четырёхугольника
Проведём BF ║АС, тогда четырёхугольник АВСD – равнобедренная трапеция,
∠ DBC = ∠ DKC (по свойству соответственных углов при BF║AC и секущей BD).
В вписанном четырёхугольнике DBFC ∠ DCF = 180° — ∠ DBF
Из треугольника DCF по теореме косинусов имеем: DF 2 = 25 2 + 16 2 + 2 ∙16 ∙25∙ 0,5.
Из треугольника DВF: 2R = = 2 ; R = .
Четырёхугольник ABCD со сторонами AB =5 и CD =17 вписан в окружность. Диагонали AC и BD пересекаются в точке K , причём ∠ AKB =60 ∘ . Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB =39 и CD =12 вписан в окружность. Диагонали AC и BD пересекаются в точке K , причём ∠ AKB =60° . Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB =43 и CD =4 вписан в окружность. Диагонали AC и BD пересекаются в точке K , причём ∠ AKB =60 ∘ . Найдите радиус окружности, описанной около этого четырёхугольника.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K . Найдите площадь параллелограмма, если BC =19 , а расстояние от точки K до стороны AB равно 7.
По свойству биссектрис углов параллелограмма ABM и ABN равнобедренные:
AB = BM и AB = AN, следовательно BM = AN.
Так как BM = AN и BM ║ AN, то четырёхугольник ABMN – параллелограмм, а так как AB = AN, то ABMN – ромб.
По свойству ромба ABК = MКВ = AKN (по двум катетам),
тогда KP = KS = KT = 7(как высоты равных треугольников, проведённые к соответственно равным сторонам).
Отрезки KP и KS лежат на одной прямой, ST — высота параллелограмма ABCD,
ST = SK + KT; ST = 7 + 7 =14
S ABCD = AD ∙ ST; S ABCD = 19 ∙ 7=133
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K . Найдите площадь параллелограмма, если BC =11 , а расстояние от точки K до стороны AB равно 3.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K . Найдите площадь параллелограмма, если BC =12 , а расстояние от точки K до стороны AB равно 9.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K . Найдите площадь параллелограмма, если BC =19 , а расстояние от точки K до стороны AB равно 10.
На стороне BC остроугольного треугольника ABC ( AB ≠ AC ) как на диаметре построена полуокружность, пересекающая высоту AD в точке M , AD =90 , MD =69 , H — точка пересечения высот треугольника ABC . Найдите AH .
Проведем ВЕ. Так как ВС – диаметр, то ∠ ВАС =90 ̊ , следовательно ВЕ – высота и
По свойству отрезков секущих АЕ ∙АС = АМ ∙АК.
АМ = AD – MD, AM = 90 – 69 = 21
Так как хорда МК перпендикулярна диаметру ВС, то MD = DK = 69.
AK = AM + MD + DK, AK = 21+ 69 + 69 = 159.
AEH (по двум углам: А – общий угол, углы ADC и AEH –прямые)
На стороне BC остроугольного треугольника ABC ( AB ≠ AC ) как на диаметре построена полуокружность, пересекающая высоту AD в точке M , AD =49 , MD =42 , H — точка пересечения высот треугольника ABC . Найдите AH .
На стороне BC остроугольного треугольника ABC ( AB ≠ AC ) как на диаметре построена полуокружность, пересекающая высоту AD в точке M , AD =27 , MD =18 , H — точка пересечения высот треугольника ABC . Найдите AH .
На стороне BC остроугольного треугольника ABC ( AB ≠ AC ) как на диаметре построена полуокружность, пересекающая высоту AD в точке M , AD =63 , MD =21 , H — точка пересечения высот треугольника ABC . Найдите AH .
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C . Найдите длину отрезка KP , если AP =7 , а сторона BC в 1,4 раза меньше стороны AB .
Решение:
АВР и АСК подобны (по двум углам, А – общий угол, углы АВР и АСК – вписанные, опираются на дугу РК), значит или
Тогда АВС и АРК подобны (по двум сторонам и углу между ними, так как , А – угол заключенный между пропорциональными сторонами), следовательно ;
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C . Найдите длину отрезка KP , если AK =21 , а сторона AC в 1,5 раза больше стороны BC .
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C . Найдите длину отрезка KP , если AK =9 , а сторона AC в 3 раза больше стороны BC .
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C . Найдите длину отрезка KP , если AP =6 , а сторона BC в 1,5 раза меньше стороны AB .
Из вершины прямого угла C треугольника ABC проведена высота CP . Радиус окружности, вписанной в треугольник BCP , равен 60, тангенс угла BAC равен . Найдите радиус окружности, вписанной в треугольник ABC .
САР = ВСР, тогда tg ∠ BCP = =
Пусть BP = 4x, CP = 3x, тогда BC = 5x
R BCP = = = x, x = 60, значит BP = 240, CP = 180, BC = 300
tg ∠ ВАС = , , , АС = 225
Из вершины прямого угла C треугольника ABC проведена высота CP . Радиус окружности, вписанной в треугольник BCP , равен 96, тангенс угла BAC равен . Найдите радиус окружности, вписанной в треугольник ABC .
Из вершины прямого угла C треугольника ABC проведена высота CP . Радиус окружности, вписанной в треугольник BCP , равен 24, тангенс угла BAC равен . Найдите радиус окружности, вписанной в треугольник ABC .
Из вершины прямого угла C треугольника ABC проведена высота CP . Радиус окружности, вписанной в треугольник ACP , равен 12 см, тангенс угла ABC равен 2,4 . Найдите радиус вписанной окружности треугольника ABC .
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM =7 и MB =9 . Касательная к описанной окружности треугольника ABC , проходящая через точку C , пересекает прямую AB в точке D . Найдите CD .
∠ АВС – вписанный, ∠ АВС =
∠АСD – угол между диаметром и хордой, ∠ АСD = , следовательно ∠ АВС = ∠АСD
∆DBC ∾∆DCA ( по двум углам; ∠D – общий, ∠ DВС = ∠АСD)
= , (по свойству биссектрисы треугольника)
DB = DA + AB; = + 16 ⇨ DC = 36,5
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM =5 и MB =10 . Касательная к описанной окружности треугольника ABC , проходящая через точку C , пересекает прямую AB в точке D . Найдите CD .
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM =9 и MB =12 . Касательная к описанной окружности треугольника ABC , проходящая через точку C , пересекает прямую AB в точке D . Найдите CD .
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM =10 и MB =18 . Касательная к описанной окружности треугольника ABC , проходящая через точку C , пересекает прямую AB в точке D . Найдите
В треугольнике ABC известны длины сторон AB =84 , AC =98 , точка O — центр окружности, описанной около треугольника ABC . Прямая BD , перпендикулярная прямой AO , пересекает сторону AC вточке D .
Найдите CD .
Пусть прямая BD, перпендикулярная прямой АО пересекает сторону АС в точке О, а окружность – в точке К. ВК ∩ АО = L.
Так как хорда ВК перпендикулярна диаметру АМ, то BL = KL и ᴗАВ = ᴗАК.
Следовательно ∠АСВ = ∠АВК (как вписанные углы, опирающиеся на равные дуги), значит
∆ABD ∾ ∆ACB (по двум углам: ∠А – общий, ∠АСВ = ∠АВК).
В треугольнике ABC известны длины сторон AB =40 , AC =64 , точка O — центр окружности, описанной около треугольника ABC . Прямая BD , перпендикулярная прямой AO , пересекает сторону AC вточке D .
Найдите CD .
В треугольнике ABC известны длины сторон AB =30 , AC =100 , точка O — центр окружности, описанной около треугольника ABC . Прямая BD , перпендикулярная прямой AO , пересекает сторону AC в точке D .
Найдите CD .
В треугольнике ABC известны длины сторон AB =12 , AC =72 , точка O — центр окружности, описанной около треугольника ABC . Прямая BD , перпендикулярная прямой AO , пересекает сторону AC в точке D .
Найдите CD .
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника ABC .
Пусть ВЕ – биссектриса АВС, АD – медиана АВС, ВЕ = АD = 96, ВЕ ⏊ АD.
∆ BOD = ∆ BOA (BO — общая, ∠ BOD = ∠ BOA = 90 ° , ∠ OBD = ∠ OBA), тогда АВ = BD = DC и AO = OD = 48
Пусть АВ = BD = DC = x
Проведем СF ⏊ BE. ∆ AOE ∾ ∆ CFE (по двум углам), значит , но (по свойству биссектрисы треугольника), тогда = ; , CF = 96
Так как BD = DC и OD ∥ FC, то по теореме Фалеса ВО = ОF.
Пусть OE = y, EF = 2y, тогда OB = 3y, BE = 4y; ВЕ = 96, 4у = 96, у = 24, ОВ = 72
В ∆ BOD: BOD = 90 ° , OD = 48, OB = 72, тогда BD = = = 8 = 24 ⇨ AB = BD = 24 , BC = 48
∆ AOE: AO = 48, OE = 24, AOE = 90 °; AE = = 24 ⇨ CE = 48 AC = 72 .
Ответ: 24 , 48 , 72 .
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 168. Найдите стороны треугольника ABC .
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 16. Найдите стороны треугольника ABC .
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 164. Найдите стороны треугольника ABC .
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC .
В ∆ АВС АН = СН = 6( по условию)
СН = СЕ = СD = 6 (по свойству отрезков, касательных к окружности).
Проведем радиусы окружностей OD и KE; D и Е – точки касания окружностей с касательной ВС, следовательно OD ⏊ BC и KE ⏊ BC, значит OD ∥ KE, тогда четырёхугольник KEDO – трапеция.
Пусть КН = КЕ = х. Проведем КР ∥ ЕD. В ∆ОКР имеем: КР = 12, ОК = 7,5 + х, ОР = 7,5 – х
По теореме Пифагора: ОК 2 = ОР 2 + КР 2 ; (7,5 + х) 2 = (7,5 – х) 2 + 12 2
30х = 144; х = 4,8. Итак, R = х =4,8.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC .
Основание AC равнобедренного треугольника ABC равно 8. Окружность радиуса 5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC .
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 6 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC .
Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD .
Проведем радиусы окружностей ОА и РС. Так как радиусы проведены в точки касания окружностей с прямой АС, то они перпендикулярны к касательной: ОА ⏊ АС и РС ⏊ АС , следовательно ОА ∥ РС. Четырёхугольник ОАРС – трапеция. ОА = 25, РС = 100, ОР = 125. Проведем ОЕ ∥ АС. В ∆РОЕ: ∠ОЕР = 90°, РЕ = 100 – 25 = 75, ОР = 125. По теореме Пифагора
ОЕ 2 = ОР 2 – РЕ 2 , ОЕ = = = 100, ОЕ = АС = 100.
∆SOA ∾∆SPC (∠S – общий, ∠SAO =∠ SCP). , , 4 = 1 + , SA = .
∆SFC: cos , SC = SA + AC = , SF =
Окружности радиусов 45 и 55 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD .
Окружности радиусов 42 и 84 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD .
Окружности радиусов 4 и 60 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD .
Видео:2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

По теме: методические разработки, презентации и конспекты
Логические задачи для 5 класса по математике
Логические задачи по математике для 5 класса, для детей, которые интересуются математикой.
Презентация «Ожившие задачи и теоремы» (ЖМ) учителя математики Монаковой Клары Захаровны.
Задачи на построение и теоремы (7-8 класс) выполнены в прогамме «Живая геометрия» как пример применения этой программы в преподавании геометрии.
Решение задач С4 на ЕГЭ по математике
Материал для консультации. Может быть полезен учителям и учащимся 9 — 11 классов при подготовке к экзаменам.
Задачи на работу. ЕГЭ по математике В13.
Решение задач на работу. Подробно, с объяснениями, разные типы задач (более десяти). Необходимо для подготовки к ЕГЭ по математике в части В13.
Задачи на работу. ЕГЭ по математике В13.
Решение задач на работу. С объяснениями, понятно доступно. Для выпускников, подготовка к ЕГЭ.
Задачи межпредметного смысла на уроках математики. Задачи природно — экологического содержания для 6 класса
Данная презентация содержит задачи экологической направленности и может быть полезна учителям математики при подготовке уроков и внеклассных мероприятий по ФГОС.
Методическая разработка по математике «Решение тестовых задач Единого Государственного Экзамена по математике: задачи на движение»
Решения тестовых задач ЕГЭ по математике по теме «Задачи на движение» всегда вызывают сложности у учащихся. Методическая разработка сделана для того ,чтоб было более ясно и проще выполнять данные зада.
📽️ Видео
Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

Как правильно решить задание про четырёхугольник? / Разбор заданий на ОГЭ по геометрииСкачать

Решение задачи 25 из ОГЭ по математике 9 классСкачать

№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Вписанный четырёхугольник | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис ТрушинСкачать

Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

ОГЭ Задание 25 Свойства вписанного и описанного четырехугольникаСкачать

Геометрия , задание 17 (часть 2)Скачать

Четырехугольник, вписанный в окружностьСкачать
ЕГЭ 2023 математика Вариант 5 задача 1Скачать
2122 в четырёхугольник ABCD вписана окружность AB равно 17 CD равно 22Скачать

Задание 17 (В1) ОГЭ по математике ▶ №12 (Минутка ОГЭ)Скачать