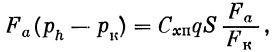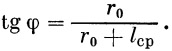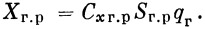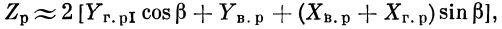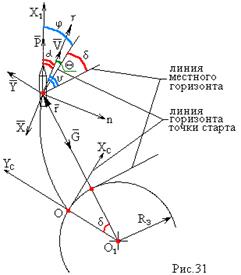
Θ – угол траектории (угол наклона траектории к горизонту) – угол между вектором скорости и линией горизонта точки старта в плоскости стрельбы .
υ –угол траектории относительно местного горизонта – угол между вектором скорости и линией местного горизонта .
δ– полярный угол , характеризует наклонение плоскости местного горизонта к плоскости точки старта .
α – угол атаки – угол между вектором скорости и продольной осью ракеты (для плоской задачи) .
Дата добавления: 2015-08-11 ; просмотров: 1385 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
- ПРИБЛИЖЕННАЯ МЕТОДИКА ПРОЕКТИРОВОЧНОГО БАЛЛИСТИЧЕСКОГО РАСЧЕТА ПЕРВЫХ СТУПЕНЕЙ РАКЕТ-НОСИТЕЛЕЙ Текст научной статьи по специальности « Механика и машиностроение»
- Аннотация научной статьи по механике и машиностроению, автор научной работы — Мухамедов Л.П., Кириевский Д.А.
- Похожие темы научных работ по механике и машиностроению , автор научной работы — Мухамедов Л.П., Кириевский Д.А.
- APPROXIMATE METHODOLOGY FOR DESIGN BALLISTIC CALCULATIONS OF THE FIRST STAGE OF LAUNCH VEHICLES
- Текст научной работы на тему «ПРИБЛИЖЕННАЯ МЕТОДИКА ПРОЕКТИРОВОЧНОГО БАЛЛИСТИЧЕСКОГО РАСЧЕТА ПЕРВЫХ СТУПЕНЕЙ РАКЕТ-НОСИТЕЛЕЙ»
- Угол наклона вектора скорости к местному горизонту
- 🎥 Видео
Видео:Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

ПРИБЛИЖЕННАЯ МЕТОДИКА ПРОЕКТИРОВОЧНОГО БАЛЛИСТИЧЕСКОГО РАСЧЕТА ПЕРВЫХ СТУПЕНЕЙ РАКЕТ-НОСИТЕЛЕЙ Текст научной статьи по специальности « Механика и машиностроение»
Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Аннотация научной статьи по механике и машиностроению, автор научной работы — Мухамедов Л.П., Кириевский Д.А.
На начальном этапе разработки новых образцов ракет-носителей проводят так называемые проектировочные баллистические расчеты. Актуальность задач проектной баллистики заметно возрастает в связи с проблемами освоения дальнего космоса и создания ракетно-космических комплексов нового поколения, требующих значительных финансовых затрат. При разработке проектировочных методик модели движения по точности не должны уступать неопределенностям исходных данных, а алгоритм методик должен отражать взаимосвязь проектных параметров с летными характеристиками ракеты . Эти принципы положены в основу предлагаемой методики баллистического расчета активного участка траектории первых ступеней ракет-носителей тяжелого и сверхтяжелого классов. Методика базируется на результатах анализа большого числа траекторий, отвечающих вариациям различных исследуемых факторов. Расчеты траекторий выполнены методом численного интегрирования дифференциальных уравнений движения в широком диапазоне варьирования проектно-баллистических параметров и граничных условий. Проведенный анализ позволил выявить некоторые общие закономерности управляемого движения и получить структуру расчетных зависимостей в аналитической форме.
Видео:Угол между векторами. 9 класс.Скачать

Похожие темы научных работ по механике и машиностроению , автор научной работы — Мухамедов Л.П., Кириевский Д.А.
Видео:Бросок под углом к горизонтуСкачать

APPROXIMATE METHODOLOGY FOR DESIGN BALLISTIC CALCULATIONS OF THE FIRST STAGE OF LAUNCH VEHICLES
The initial stages of development of new types of launch vehicles involve performing the so-called design ballistic calculations. Currently, the relevance of design ballistics tasks is noticeably increasing in connection with the problems of deep space exploration and the creation of a new generation of space rocket systems, requiring significant financial investment. When developing design methods, motion models should not be inferior in accuracy to the uncertainties of the source data, and the algorithm of the technique should reflect the relationship of design parameters with the flight characteristics of the rocket. These principles formed the basis of the proposed methods for ballistic calculations of the active section of the trajectory of the first stages of heavy and super heavy launch vehicles. The technique is based on the results of the analysis of numerous trajectories corresponding to variations of various studied factors. The trajectory calculations were carried out using the method of numerical integration of differential equations of motion in a wide range of variation of design ballistic parameters and boundary conditions. The analysis made it possible to identify some general patterns of the controlled motion and to obtain the structure of the calculated dependencies in an analytical form.
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Текст научной работы на тему «ПРИБЛИЖЕННАЯ МЕТОДИКА ПРОЕКТИРОВОЧНОГО БАЛЛИСТИЧЕСКОГО РАСЧЕТА ПЕРВЫХ СТУПЕНЕЙ РАКЕТ-НОСИТЕЛЕЙ»
УДК 629.7.01, 629.76, 626.78 doi: 10.18698/0536-1044-2020-6-67-77
Приближенная методика проектировочного баллистического расчета первых ступеней ракет-носителей
Л.П. Мухамедов1, Д.А. Кириевский2
1 МГТУ им. Н.Э. Баумана
2 АО «ГКНПЦ имени М.В. Хруничева»
for Design Ballistic Calculations of the First Stage
of Launch Vehicles
L.P. Muhamedov1, D.A. Kirievskii2
1 Bauman Moscow State Technical University
2 AO Khrunichev State Research and Production Space Center
На начальном этапе разработки новых образцов ракет-носителей проводят так называемые проектировочные баллистические расчеты. Актуальность задач проектной баллистики заметно возрастает в связи с проблемами освоения дальнего космоса и создания ракетно-космических комплексов нового поколения, требующих значительных финансовых затрат. При разработке проектировочных методик модели движения по точности не должны уступать неопределенностям исходных данных, а алгоритм методик должен отражать взаимосвязь проектных параметров с летными характеристиками ракеты. Эти принципы положены в основу предлагаемой методики баллистического расчета активного участка траектории первых ступеней ракет-носителей тяжелого и сверхтяжелого классов. Методика базируется на результатах анализа большого числа траекторий, отвечающих вариациям различных исследуемых факторов. Расчеты траекторий выполнены методом численного интегрирования дифференциальных уравнений движения в широком диапазоне варьирования проектнобаллистических параметров и граничных условий. Проведенный анализ позволил выявить некоторые общие закономерности управляемого движения и получить структуру расчетных зависимостей в аналитической форме.
Ключевые слова: методика проектировочного баллистического расчета, задачи проектной баллистики, проектно-баллистические параметры, ракета-носитель, летные характеристики ракеты, потери характеристической скорости
The initial stages of development of new types of launch vehicles involve performing the so-called design ballistic calculations. Currently, the relevance of design ballistics tasks is noticeably increasing in connection with the problems of deep space exploration and the creation of a new generation of space rocket systems, requiring significant financial investment. When developing design methods, motion models should not be inferior in accuracy to the uncertainties of the source data, and the algorithm of the technique should reflect the relationship of design parameters with the flight characteristics of the rocket. These principles formed the basis of the proposed methods for ballistic calculations of the active section of the trajectory of the first stages of heavy and super heavy launch vehicles. The technique is based on the results of the analysis of numerous trajectories corresponding to variations of
various studied factors. The trajectory calculations were carried out using the method of numerical integration of differential equations of motion in a wide range of variation of design ballistic parameters and boundary conditions. The analysis made it possible to identify some general patterns of the controlled motion and to obtain the structure of the calculated dependencies in an analytical form.
Keywords: design ballistic calculation methods, design ballistics tasks, design and ballistic parameters, launch vehicle, launch vehicle flight characteristics, characteristic speed losses
Основной задачей современной пилотируемой космонавтики является переход от полетов на околоземные орбиты к освоению более отдаленных областей космического пространства 2. Весьма вероятно, что в недалеком будущем Россия примет участие в создании Международной лунной космической станции 6.
Необходимость в постоянно действующей космической базе на Луне объясняется тем, что к 2024 г. закончится срок эксплуатации Международной космической станции, а Луна может быть использована в качестве стартовой площадки для межпланетных перелетов [7]. Создание и обслуживание такой станции невозможно без разработки ракет-носителей (РН) сверхтяжелого класса (СТК), способных выводить полезную нагрузку массой около 100 т на низкую опорную орбиту (НОО) 8.
Проектирование новых образцов РН СТК представляет собой длительный многоэтапный итерационный процесс. В связи с этим на начальном этапе разработок возникает потребность в универсальных проектировочных методиках баллистических расчетов, определяющих допустимые границы значений основных проектных параметров РН и обеспечивающих выбор их оптимальных сочетаний с учетом требований технического задания 12. В дальнейшем эти параметры используют в качестве граничных условий при решении частных задач баллистического проектирования.
Цель работы — создание методики проектировочного баллистического расчета первых ступеней (ПС) РН, предназначенных для доставки полезной нагрузки с поверхности Земли на НОО.
Расчетные зависимости представлены в аналитической форме. Как показала практика, применение высокоточных методов на данном этапе разработок малоэффективно. Это объясняется следующими причинами. Во-первых, несмотря на высокое быстродействие современных компьютеров, использование программных средств может привести к неоправданным временным и материальным затратам.
Во-вторых, при применении методов численного интегрирования на начальной стадии проектирования возможна потеря контроля проектантом за процессом выбора оптимальных проектно-конструктивных решений.
Таким образом, методика проектировочного баллистического расчета должна позволять быстро с требуемой точностью, без громоздких вычислений и численного интегрирования определять траекторные переменные РН по ее проектным параметрам. Одним из необходимых условий при разработке подобных методик является представление окончательных расчетных зависимостей в аналитической форме, так как использование аналитических расчетных соотношений дает возможность сократить на несколько порядков время решения краевых задач [13].
Говоря о преимуществах приближенных аналитических методов, авторы статьи ни в коей мере не умаляют роль баллистических расчетов с применением программных средств и алгоритмических языков высокого уровня. Напротив, результаты баллистических расчетов, полученных методом численного интегрирования уравнений движения, использованы в работе при построении аналитических соотношений, связывающих значения траекторных переменных в характерных точках активного участка траектории (АУТ) ПС РН с проектнобаллистическими параметрами (ПБП).
Под ПБП следует понимать минимальную совокупность параметров, однозначно определяющих алгоритм проектно-баллистических расчетов на ранних этапах разработок.
Методическая часть. Для ПС РН имеем пять независимых ПБП.
1. Относительная конечная масса первой ступени
где тк — конечная масса ПС; т0 — стартовая масса РН.
2. Удельный импульс тяги двигательной установки в пустоте
Здесь Рп — суммарная пустотная тяга двигательной установки ПС с учетом потерь характеристической скорости на управление; m — абсолютное постоянное значение массового секундного расхода топлива,
где m — текущая масса РН; t — время полета; д — относительная масса ПС.
3. Коэффициент увеличения удельного импульса тяги в пустоте
где Р0 — суммарная тяга двигательной установки ПС у Земли с учетом потерь на органы управления; I0 — удельный импульс тяги двигательной установки ПС у Земли.
4. Стартовая нагрузка на тягу или коэффициент тяговооруженности
_ Щ)g0 _ m0g0kp v0 =—
где g0 = 9,81 м/с2 — осредненное по поверхности Земли ускорение свободного падения.
5. При проектировании баллистических ракет для оценки влияния аэродинамических сил на летно-технические характеристики ракеты обычно используют стартовую нагрузку на мидель рм , равную отношению стартового веса (или стартовой массы) к площади миделева сечения [11, 12, 15]. Для РН СТК корректнее, на наш взгляд, вместо рм использовать более комплексный параметр, который назовем баллистическим коэффициентом
где Sm — площадь миделева сечения ракеты; cxmax — максимальное значение коэффициента силы лобового сопротивления РН, рассчитанное при нулевом угле атаки а, числе Маха M = 1,07 и высоте полета h = 7 км.
В качестве проектно-баллистического будем также рассматривать комплексный параметр — характеристическую (идеальную) скорость ПС
РН vхар = — 1п ln Дк .
Расчеты численным методом проведены при следующих общепринятых допущениях:
• Земля — сферическая, поле ее тяготения — центральное;
• движение относительно центра масс РН не рассматривается;
• управление — идеальное, управляющие силы пренебрежимо малы;
• траектория движения РН лежит в плоскости НОО;
• суточное вращение Земли отсутствует;
• параметры атмосферы соответствуют ГОСТ 4401-81;
• коэффициент силы лобового сопротивления cx = cxcxmax (cx — безразмерный коэффициент лобового сопротивления); в таблице приведен единый для РН закон изменения
cx от числа Маха с учетом используемых методик и результатов работ [14, 16-18].
При формировании системы уравнений движения использованы следующие системы координат (рис. 1):
Видео:Физика: Понятие Вектор, Вектор СкоростиСкачать

Угол наклона вектора скорости к местному горизонту
С.П. Королёв
Основы проектирования
баллистических ракет дальнего действия
(курс лекций)
МВТУ ИМ. БАУМАНА 1949
ЛЕКЦИЯ ЧЕТВЕРТАЯ
3. Вопросы прочности ракет дальнего действия. Расчетные случаи и схемы нагружения
По прочности ракет дальнего действия отсутствуют какие-либо методические материалы. Излагаемые ниже расчетные случаи и схемы нагружения, используемые при расчете на прочность ракет дальнего действия, являются первой попыткой систематизировать существующие в этой области отдельные расчеты, результаты статических испытаний и некоторые результаты обработки летных испытаний.
Необходимость достаточно достоверной методики для расчетной и экспериментальной проверки прочности конструкции ракет очевидна.
Вопросы веса неизменно связаны с вопросами прочности, а вес (и отсюда μ к) для ракет дальнего действия, как мы уже убедились ранее, имеет исключительное значение.
Необычайно сложная и разнообразная картина действующих на ракету сил, сложная структура внешних возмущений и возможных случаев нагружения и т. п. в совокупности создают исключительные трудности при разработке хотя бы приближенной общей методики расчета.
В силу этого, а также из-за недостаточной изученности явлений, происходящих, например, при прохождении ракетой околозвуковой области, недостаточной изученности и отсутствия опытных данных по вибрациям эти и ряд аналогичных расчетных случаев в дальнейшем изложении подробно не разбираются.
Принятая схема расчетных случаев имеет в известной степени условный характер, приспособленный для решения практических задач.
В последнем разделе приводятся примеры прочностных расчетов элементов ракеты.
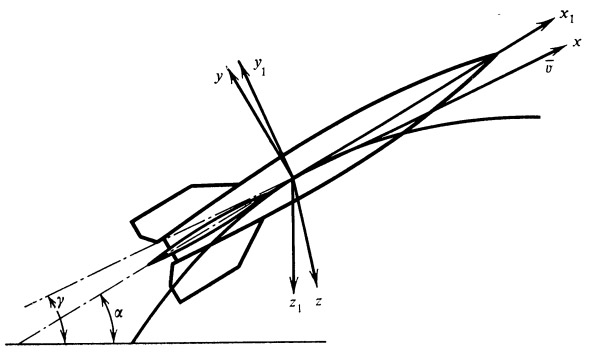 Рис. 21. Системы координат |
| Основные обозначения | |
| G — полетный вес ( кг ), М — масса ( кг • сек / м ), Р — тяга ( кг ), Q — лобовое сопротивление ( кг ), Y — подъемная сила ( кг ), Т — осевая нагрузка ( кг ), N — поперечная нагрузка ( кг ), v — скорость ракеты ( м / сек ), u — скорость ветра ( м / сек ), ρ — плотность воздуха ( кг • сек 2 / м 4 ) q — скоростной напор, q = ( ρ v 2 )/2( кг / м 2 ), Z — боковая сила ( кг ), М — момент относительно оси ракеты ( кг • м ), n — коэффициент перегрузки, f — коэффициент безопасности, | S — площадь характерной поверхности (миделя) ( м 2 ), t — время работы двигателя ( сек ), α — угол атаки, γ — угол наклона вектора скорости к горизонту, ω — угловая скорость относительно оси ракеты 1/ сек ), ( dw / dt ) — угловое ускорение относительно оси ракеты 1/ сек 2 ), ṁ — секундный массовый расход ( кг • сек / м ), р — удельное давление ( кг / м 2), F — инерционная сила, R — аэродинамическая сила, R y — управляющая сила. |
Системы координат
1. Связанная система координат ( х 1, у 1, z 1) с началом координат в центре тяжести ракеты. Ось x 1 направлена по продольной оси ракеты, ось у 1 в плоскости I—III, ось z 1 в плоскости II—IV.
2. Скоростная система координат ( х , у , z ) с началом координат в центре тяжести ракеты. Ось х направлена по вектору скорости, у — по нормали вверх и z — по бинормали (рис. 21).
В полете на ракету кроме силы тяжести G и тяги Р действуют силы, зависящие от характера движения в пространстве. К ним относятся (рис. 22): аэродинамические силы, обусловленные движением ракеты в воздушной среде; управляющие силы, обеспечивающие полет по заданной программе; инерционные силы, возникающие вследствие наличия ускоренного движения ракеты по криволинейной траектории.
 Рис. 22. Силы, действующие на ракету в полете |
В дальнейшем вес и силы инерции будем называть массовыми силами, а все остальные силы — поверхностными.
Тяга двигателя на любой высоте равна
| P и = ṁC и + F а( p и— p к), | (1) |
где С и — истинная скорость истечения, F a — площадь выходного сечения сопла, р с — давление выходящего газа на срезе сопла, р к — давление за кормой ракеты на высоте Н . Тяга Ри может быть выражена через начальную тягу Р 0 у Земли посредством элементарных преобразований:
| P o = ṁC и + F a ( p c— p a), | (2) |
Подставив значение ṁС и из формулы (2)) в формулу (1)), получим для Р и выражение
| P и = Р 0 — F a ( p a — p h) + F a ( p h — р к) . | (3) |
Величина F a( p h— p к) есть не что иное, как величина, равная силе сопротивления подсоса и обратно ей направленная, т. е.
где F к — площадь кормового среза корпуса.
3.1. Силы, действующие на ракету в полете
Исключив ее из формулы (3), находим тягу
| P = P 0 + F а ( p a— p h) | (4) |
2. Аэродинамические силы
Зависимость аэродинамической силы от параметров траектории и геометрии ракеты может быть выражена формулой
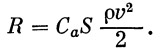 | (5) |
Обычно рассматриваются составляющие аэродинамической силы в скоростной системе координат:
а) составляющая по скорости (лобовое сопротивление)
| Q = C x q S , | (6) |
б) составляющая по нормали (подъемная сила)
| Y = C у qS , | (7) |
в) составляющая по бинормали (боковая сила)
| Z = C z qS . | (8) |
Лобовое сопротивление
Величина лобового сопротивления зависит от скорости полета ракеты, ее формы и размеров, высоты полета и угла атаки (при малых значениях угла атаки влиянием его на сопротивление можно пренебречь).
Сопротивление ракеты состоит из сопротивления тела вращения (корпуса) Q к и стабилизирующих поверхностей Q ст:
| Q = Q k + Q ст. | (9) |
Составляющими лобового сопротивления являются:
а) сопротивление трения (в общем случае неравномерно распределенное по всей поверхности ракеты), характеризуемое коэффициентом сопротивления трения ( С хтр); с достаточной точностью для практических целей можно принять сопротивление трения равномерно распределенным по всей поверхности;
б) волновое сопротивление ( С хв);
в) сопротивление подсоса ( С хп).
На активном участке коэффициент сопротивления подсоса будет равен
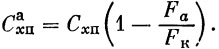 | (10) |
Общий коэффициент лобового сопротивления тогда будет равен
| C х = C хтр + C хв + C xп | (11) |
Подъемная сила
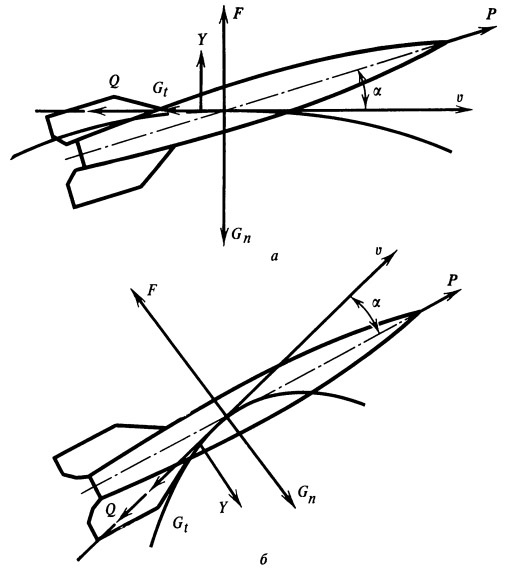 Рис. 23. Силы в случае полета по траектории с малой кривизной ( α ) и с большой кривизной ( σ ) |
При заданной программе величина подъемной силы зависит от аэродинамической характеристики корпуса ракеты, скорости и высоты полета, а также от величины угла атаки. Приближенно величину программного угла атаки можно найти, составив уравнение проекций всех внешних сил, действующих на ракету, на нормаль к траектории:
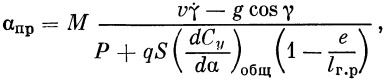 | (12) |
где е — расстояние от центра давления до центра тяжести, l г.р — расстояние от центра давления газовых рулей до центра тяжести ракеты.
Действительный угол атаки не будет равен программному вследствие наличия случайных и постоянно действующих возмущающих сил (ветровые нагрузки, эксцентриситет тяги) и колебаний оси ракеты около программного положения.
Несоответствие действительного угла атаки программному приводит к изменению величины подъемной силы и нормальной составляющей тяги. Вследствие этого нарушения равновесия сил происходит изменение кривизны траектории и возникает дополнительная центробежная сила, уравновешивающая систему (рис. 23).
Из-за вращения ракеты относительно центра тяжести возникают дополнительные углы атаки, имеющие местное значение. Кроме того, местные углы атаки возникают из-за несовершенств самой конструкции ракеты. К ним относятся: начальные углы атаки перьев стабилизатора (вследствие их перекоса) и углы атаки за счет деформации как стабилизатора, так и корпуса.
Ветровая нагрузка
К числу случайных нагрузок на ракету относится дополнительная аэродинамическая нагрузка, возникающая при полете в неспокойном воздухе. Составляющая скорости ветра u x по направлению скорости ракеты и приводит к изменению лобового сопротивления
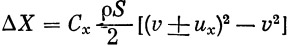 | (13) |
и имеет практическое значение лишь при скоростях ракеты, сравнимых со скоростью ветра. Нормальная составляющая скорости ветра приводит к изменению угла атаки ракеты на величину, равную приближенно
| Δα = u у/ v = α и. | (14) |
Это в свою очередь приводит к изменению величины подъемной силы или к возникновению боковой силы Z .
Считаем, что добавочная подъемная сила за счет порывов ветра направлена нормально к вектору скорости. По данным Института теоретической геофизики Академии наук СССР скорость ветра увеличивается с увеличением высоты. На больших высотах наблюдаются вихревые движения, охватывающие значительные пространства. На высоте более 100 км имеют место устойчивые потоки со скоростями до 200 м / сек .
Увеличение дополнительного угла атаки с высотой за счет увеличения скорости ветра не имеет большого практического значения из-за малой плотности воздуха на этих высотах.
При определении ветровых нагрузок рассматривается полет в зоне поперечного ветра, охватывающего весь корпус ракеты.
Однако возможны случаи резко ограниченных порывов ветра, действующих на часть ракеты. Например, при действии бокового порыва ветра на хвостовую часть ракеты вследствие косого обтекания возникает вращающий момент относительно продольной оси ракеты. Величину его, пренебрегая подъемной силой хвостовой части корпуса ракеты, можно приближенно определить из уравнения (рис. 24)
| M xu = Y I r I — ( Y II r II + Y III r III) . | (15) |
Здесь r I, II, III — расстояния от оси ракеты до центра давления перьев I , II и III ,
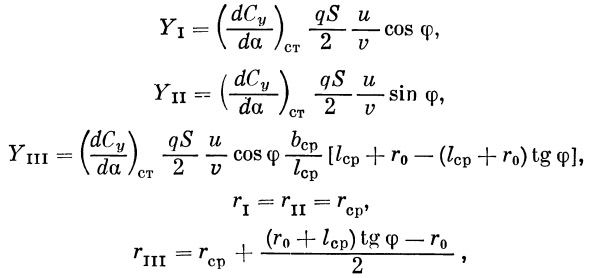 | (16) |
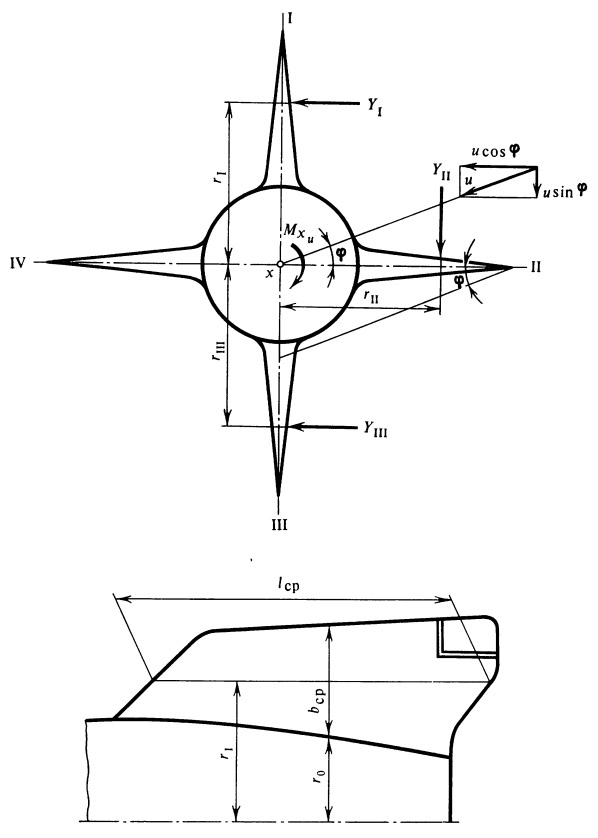 Рис. 24. Вращающий момент, действующий на хвостовую часть ракеты при порыве ветра |
где ( dC y/ d α ) ст — производная С у по углу атаки горизонтального или вертикального оперения, φ — угол наклона вектора скорости u к плоскости стабилизатора, l ср= F ст/ b ср — средний размах пера стабилизатора, b ср — средняя хорда пера стабилизатора, r 0 — радиус корпуса в сечении среднего размаха. После подстановки соотношений (16) в формулу (15) получим окончательно
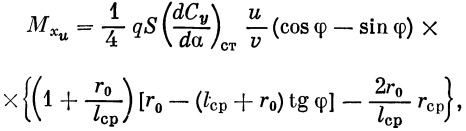 | (17) |
и max М ха будет при
Демпфирующая нагрузка
При вращении ракеты вокруг какой-либо оси, проходящей через ее центр тяжести, возникает демпфирующий момент, пропорциональный угловой скорости ω , за счет несимметричного изменения углов атаки сечений ракеты.
Величина приращения углов атаки зависит от расстояния этих сечений от оси вращения, т. е.
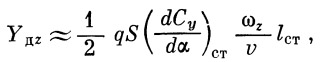 | (18) |
где ω z, ω у, ω х — угловые скорости ракеты относительно осей z , у , х . Это местное изменение углов атаки не имеет большого практического значения лишь для корпуса ракеты. При наличии же стабилизирующих плоскостей оно приводит к возникновению несимметричного загружения перьев стабилизатора. Так, например:
1. При вращении относительно одной из поперечных осей, например z , дополнительная демпфирующая нагрузка может либо суммироваться, либо вычитаться из уравновешивающей нагрузки (рис. 25) в зависимости от направления вращения.
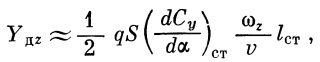 | (19) |
где l ст — расстояние от центра тяжести ракеты до центра давления пера стабилизатора.
2. В случае вращения относительно продольной оси ракеты со скоростью ωх демпфирующая нагрузка Y д, направленная в сторону, противоположную ω х, будет алгебраически складываться с уравновешивающими нагрузками Z , приложенными к перьям стабилизатора (рис. 26).
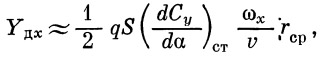 | (20) |
где ω х r ср= α ср — дополнительный средний угол атаки от вращения со скоростью ω x.
3. Управляющие силы
Устойчивый полет ракеты по заданной программе обеспечивается системой газовых и воздушных рулей.
Газовые рули
Составляющие аэродинамической нагрузки на газовые рули в связанной системе координат
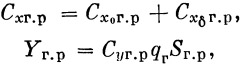 | (21) |
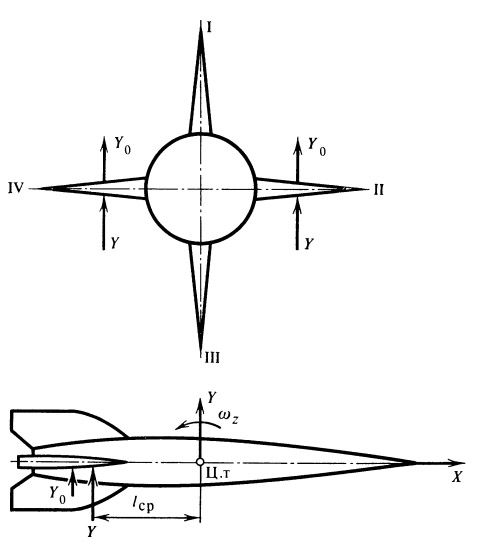 Рис. 25. Действие демпфирующей нагрузки на стабилизатор при вращении ракеты вокруг поперечной оси |
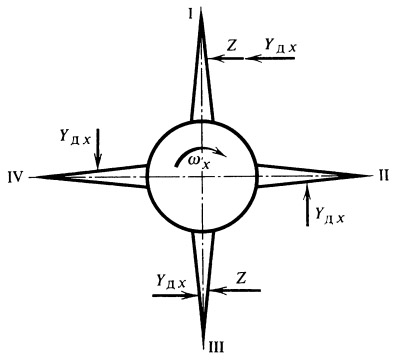 Рис. 26. Действие демпфирующей нагрузки на стабилизатор при вращении ракеты вокруг продольной оси |
где С х0г.р — коэффициент сопротивления руля при нулевом угле отклонения, С х δ гр — коэффициент сопротивления газового руля, зависящий от угла его отклонения, q r — скоростной напор газовой струи за срезом сопла, S г.р — площадь газового руля — являются переменными величинами на всем участке работы двигателя вследствие изменения площади руля из-за его обгорания и углов поворота рулей.
Воздушные рули
Нагрузки на воздушные рули определяются в скоростной системе координат.
Величина их зависит от скоростного напора, от угла отклонения и площади руля:
 | (22) |
где S в.р — площадь воздушного руля, C x в.р — коэффициент сопротивления воздушного руля, зависящий, в частности, от угла отклонения его.
Полетный вес ракеты есть функция секундного расхода ̇G и времени работы двигателя:
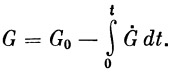 | (23) |
В общем случае секундный расход является также функцией времени.
Составляющие веса в скоростной системе координат обозначим:
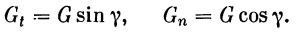 | (24) |
5. Инерционные нагрузки
Инерционные силы, возникающие вследствие наличия ускорения центра тяжести, одинаково действуют на всю массу ракеты и определяются обычно в скоростной системе координат. Составляющая инерционной нагрузки, направленная по касательной к траектории, определяется, как известно, формулой
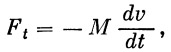 | (25) |
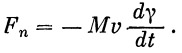 | (26) |
Инерционные нагрузки, зависящие от движения ракеты относительно ее центра тяжести, находятся в связанной системе координат и зависят как от расстояния массы от оси вращения, так и от угловых ускорений, т. е. носят местный характер:
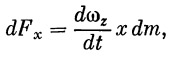 | (27) |
где dm — элементарная масса ракеты, х — расстояние от центра тяжести ракеты до центра масс dm .
6. Уравнения движения
Величины рассмотренных выше поверхностных и массовых сил должны при совместном рассмотрении удовлетворять условиям равновесия системы.
Для нахождения уравнений движения возьмем сумму проекций всех сил на скоростные координатные оси (рис. 27).
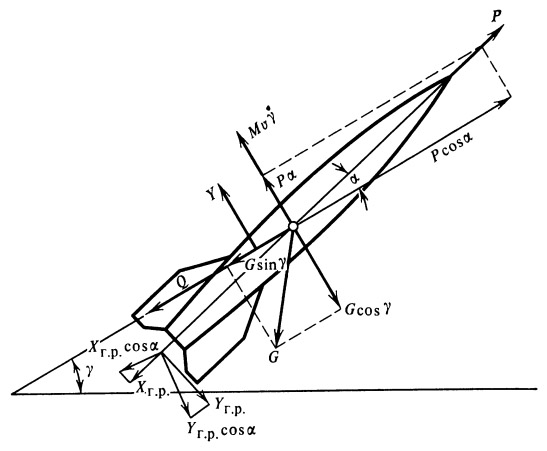 Рис. 27. К выводу уравнений движения ракеты в скоростной системе координат |
Проекция сил на касательную к траектории
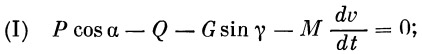 | (28) |
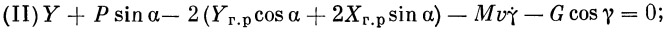 | (29) |
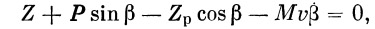 | (30) |
β — угол рыскания, γ — угол наклона касательной к траектории к плоскости начального горизонта.
Сумма всех моментов относительно связанных осей координат:
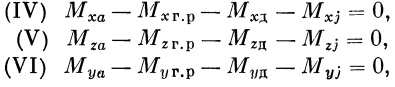 | (31) |
где М ха — момент относительно оси х от аэродинамических сил, М хг.р — момент управляющих сил, М х.д — демпфирующий момент, M xj — инерционный момент.
7. Коэффициенты перегрузок
Величину всех массовых сил, действующих на ракету, характеризуем их отношением к весу ракеты в рассматриваемый момент времени. Это отношение называется коэффициентом перегрузки.
Из уравнений равновесия сил легко установить, что сумма всех массовых сил равна сумме поверхностных нагрузок. Следовательно, коэффициент перегрузки можно определить через отношение всех поверхностных сил к полетному весу ракеты.
Рассмотрим составляющие перегрузки в скоростной системе координат.
Тангенциальная инерционная нагрузка F x, складываясь с тангенциальной составляющей веса G sin γ дает перегрузку, равную
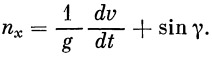 | (32) |
Для практических расчетов удобнее выражать коэффициент тангенциальной перегрузки через поверхностные силы:
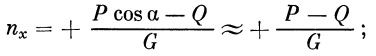 | (32′) |
для малых углов атаки можно принять cos α ≈1. Так как центробежная инерционная сила, зависящая от характера действительной траектории ( ̇γ и v ), разгружает ракету от нормальной составляющей веса, то коэффициент нормальной перегрузки будет равен
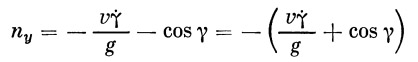 | (33) |
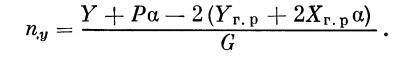 | (33′) |
Аналогично коэффициент боковой перегрузки
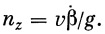 | (34) |
В связанной системе координат перегрузку в направлении продольной оси называем осевой перегрузкой:
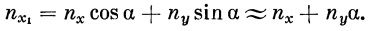 | (35) |
При достаточно малых значениях n y и α по сравнению с n х их произведением можно пренебречь, т. е. считать, что
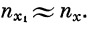 | (35′) |
Составляющую перегрузки в направлении оси y назовем поперечной перегрузкой. Величина ее может значительно отличаться от величины нормальной перегрузки (при больших значениях осевой перегрузки):
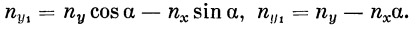 | (36) |
Местный коэффициент поперечной перегрузки с учетом вращения ракеты относительно оси z определяется как сумма
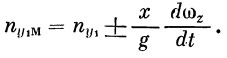 | (37) |
При свободном полете ракеты, т. е. при отсутствии тяги, коэффициент тангенциальной перегрузки будет равен
| n х = Q / G . | (38) |
Если при этом отсутствуют какие-либо возмущающие силы, то нормальная перегрузка будет равна
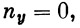 | (39) |
а при их наличии она находится как отношение подъемной силы к весу ракеты
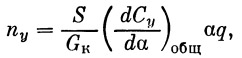 | (39′) |
где G к — конечный вес ракеты, α — угол атаки от возмущающих сил.
🎥 Видео
Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

Урок 40. Задачи на движение тела, брошенного под углом к горизонту (ч.1)Скачать

Нахождение угла между векторами через координаты. 9 класс.Скачать

Как находить угол между векторамиСкачать

Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

9 класс, 17 урок, Угол между векторамиСкачать

105. Угол между векторамиСкачать

Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

2.4. Радиус-вектор и вектор перемещенияСкачать

Определение параметров движения по заданному радиус-вектору. Векторный способ задания движения.Скачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Радиус векторСкачать

Лекция 4. ВЕКТОРА │ кинематика с нуляСкачать

Урок 9. Проекции вектора на координатные осиСкачать