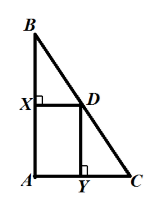4 замечательные точки окружности и их свойства (5 видео)

Замечательные точки окружности. I. Математический диктант Вариант 1 1. Биссектрисой треугольника называется … 2. Высотой треугольника называется … 3. — презентация

Презентация была опубликована 8 лет назад пользователемВиталий Недоплясов

Содержание

Похожие презентации
Презентация на тему: » Замечательные точки окружности. I. Математический диктант Вариант 1 1. Биссектрисой треугольника называется … 2. Высотой треугольника называется … 3.» — Транскрипт:
Четыре замечательные точки треугольника
Точка пересечения медиан треугольника
Точка пересечения биссектрис треугольника
Готовые работы на аналогичную тему
Точка пересечения серединных перпендикуляров треугольника
Точка пересечения высот треугольника
Пример задачи на использование 4 замечательных точек треугольника
Замечательное свойство окружности.
🎦 Видео

Презентация на тему: » Замечательные точки окружности. I. Математический диктант Вариант 1 1. Биссектрисой треугольника называется … 2. Высотой треугольника называется … 3.» — Транскрипт:

1 Замечательные точки окружности

2 I. Математический диктант Вариант 1 1. Биссектрисой треугольника называется … 2. Высотой треугольника называется … 3. Если точка пересечения серединных перпендикуляров сторон треугольника находится вне его, то … 4. Треугольник имеет … медиан. Вариант 2 1. Медианой треугольника называется … 2. Серединным перпендикуляром стороны треугольника называется … 3. Если точка пересечения серединных перпендикуляров сторон треугольника находится на его стороне, то … 4. Треугольник имеет … биссектрис.

3 Новый материал Изобразим треугольник ABC: а) остроугольный; б) прямоугольный; в) тупоугольный. Проведем все его высоты. Сделаем соответствующее предположение и докажем следующую теорему.

4 Теорема. Высоты треугольника или их продолжения пересекаются в одной точке (ортоцентре треугольника).

5 Доказательство. Через вершины данного треугольника АВС проведем прямые, параллельные противоположным сторонам.

7 Заметим, что высоты треугольника могут не пересекаться. Изображен тупоугольный треугольник ABC, в котором продолжения высот AA1, BB1, CC1 пересекаются в одной точке H, а сами высоты не пересекаются. не пересекаются.

8 Задание Изобразим треугольник ABC: а) остроугольный; б) прямоугольный; в) тупоугольный. Проведем все его медианы. Сделаем соответствующее предположение о том, что все медианы треугольника пересекаются в одной точке. Теперь измерим все медианы от вершины до точки пересечения всех медиан, и от этой точки до соответствующей стороны. Сделаем предположение об отношении, в котором делит каждую медиану точка их пересечения и докажем следующую теорему.

9 Теорема. Медианы треугольника пересекаются в одной точке (центроиде треугольника), и делятся в этой точке в отношении 2:1, считая от вершин.

10 Доказательство. В треугольнике АВС проведем медианы АD и ВЕ и их точку пересечения обозначим через О. Отрезок ED будет средней линией треугольника АВС. Проведем среднюю линию HG в треугольнике АВО. Треугольники HGO и EDO равны (по второму признаку равенства треугольников). Следовательно, HO=OE и GO=OD. Таким образом, имеем AG=GO=OD, BH=HO=OE, т.е. медианы АD и BE в точке пересечения делятся в отношении 2:1, считая от соответствующей вершины. Медиана, проведенная из вершины С, также должна делить медиану АD в отношении 2:1. Следовательно, она будет проходить через точку О, т.е. все три медианы будут пересекаться в одной точке.

14 VI. Задание на дом 1. Выучить разобранную на уроке теорию (п. 38 учебника). 2. Решить задачи.7,8,11,22,23

Видео:Замечательные точки треуг-ка. 8 класс.Скачать

Четыре замечательные точки треугольника

Вы будете перенаправлены на Автор24

В треугольнике есть так называемые четыре замечательные точки: точка пересечения медиан. Точка пересечения биссектрис, точка пересечения высот и точка пересечения серединных перпендикуляров. Рассмотрим каждую из них.

Видео:Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

Точка пересечения медиан треугольника

О пересечении медиан треуголника: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.

Доказательство.

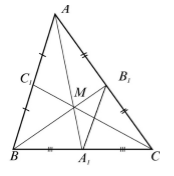
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 1).

Рисунок 1. Медианы треугольника

По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $angle ABB_1=angle BB_1A_1, angle BAA_1=angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда

Аналогично доказывается, что

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Точка пересечения биссектрис треугольника

О пересечении биссектрис треугольника: Биссектрисы треугольника пересекаются в одной точке.

Доказательство.

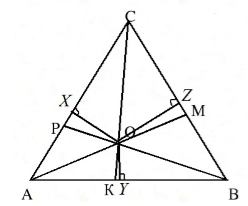
Рассмотрим треугольник $ABC$, где $AM, BP, CK$ его биссектрисы. Пусть точка $O$ — точка пересечения биссектрис $AM и BP$. Проведем из этой точки перпендикуляры к сторонам треугольника (рис. 2).

Рисунок 2. Биссектрисы треугольника

Готовые работы на аналогичную тему

Для доказательства нам потребуется следующая теорема.

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

По теореме 3, имеем: $OX=OZ, OX=OY$. Следовательно, $OY=OZ$. Значит точка $O$ равноудалена от сторон угла $ACB$ и, значит, лежит на его биссектрисе $CK$.

Видео:четыре замечательные точки треугольника 8 КЛАСС АтанасянСкачать

Точка пересечения серединных перпендикуляров треугольника

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство.

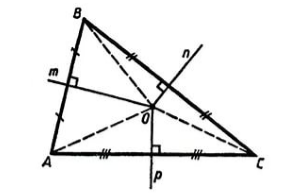
Пусть дан треугольник $ABC$, $n, m, p$ его серединные перпендикуляры. Пусть точка $O$ — точка пересечения серединных перпендикуляров $n и m$ (рис. 3).

Рисунок 3. Серединные перпендикуляры треугольника

Для доказательства нам потребуется следующая теорема.

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов данного отрезка.

По теореме 3, имеем: $OB=OC, OB=OA$. Следовательно, $OA=OC$. Значит точка $O$ равноудалена от концов отрезка $AC$ и, значит, лежит на его серединном перпендикуляре $p$.

Видео:Геометрия 8 класс. Четыре замечательные точки треугольникаСкачать

Точка пересечения высот треугольника

Высоты треугольника или их продолжения пересекаются в одной точке.

Доказательство.

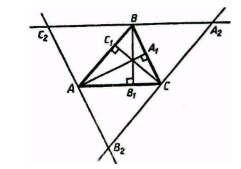
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его высоты. Проведем через каждую вершину треугольника прямую, параллельную противоположной вершине стороне. Получаем новый треугольник $A_2B_2C_2$ (рис. 4).

Рисунок 4. Высоты треугольника

Так как $AC_2BC$ и $B_2ABC$ параллелограммы с общей стороной, то $AC_2=AB_2$, то есть точка $A$ — середина стороны $C_2B_2$. Аналогично, получаем, что точка $B$ — середина стороны $C_2A_2$, а точка $C$ — середина стороны $A_2B_2$. Из построения мы имеем, что $_1bot A_2B_2, _1bot A_2C_2, _1bot C_2B_2$. Следовательно, $_1, _1, _1$ — серединные перпендикуляры треугольника $A_2B_2C_2$. Тогда, по теореме 4, имеем, что высоты $_1, _1, _1$ пересекаются в одной точке.

Видео:Четыре замечательные точки треугольника. Видеоурок 20. Геометрия 8 классСкачать

Пример задачи на использование 4 замечательных точек треугольника

Серединные перпендикуляры к сторонам $AB$ и $AC$ треугольника $ABC$ пересекаются в точке $D$ стороны $BC$. Докажите, что

а) точка $D$ — середина стороны $BC$.

б) $angle A=angle B+angle C$

Решение.

а) По теореме 4, все серединные перпендикуляры пересекаются в точке $D$. Следовательно, $D$ — основание серединного перпендикуляра к стороне $BC$. Значит точка $D$ — середина стороны $BC$.

б) Так как $X$ и $D$ — середины сторон, то $XD$ — средняя линия треугольника. Тогда, по теореме о средней линии треугольника $XD||AC$. Значит,$angle A=angle DXB$, как соответственные углы. Значит, $angle A=^0$. Тогда$angle B+angle C=^0-angle A=^0-^0=^0=angle A$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 29 03 2022

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Замечательное свойство окружности.

ОКРУЖНОСТЬ

i. 1. Окружность.Окружностью называется геометрическое место точек плоскости, удаленных от данной точки, называемой центром окружности, на одно и то же положительное расстояние.

ii. Свойства окружности.

1) Диаметр, перпендикулярный хорде, делит ее пополам.

2) Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.

3) Серединный перпендикуляр к хорде проходит через центр окружности.

5) Равные хорды удалены от центра окружности на равные расстояния.

6) Хорды окружности, удаленные от центра на равные расстояния, равны.

7) Окружность симметрична относительно любого своего диаметра.

8) Дуги окружности, заключенные между параллельными хордами, равны.

9) Из двух хорд больше та, которая менее удалена от центра.

10) Диаметр есть наибольшая хорда окружности.

Замечательное свойство окружности.

1) Геометрическое место точек M, из которых отрезок AB виден под прямым углом (ÐAMB =90 0 ), есть окружность с диаметром AB без точек A и B.

2) Геометрическое место точек M, из которых отрезок AB виден под острым углом (ÐAMB 0 ) есть внешность круга с диаметром АВ без точек прямой AB.

3) Геометрическое место точек M, из которых отрезок AB виден под тупым углом (ÐAMB > 90 0 ), есть внутренность круга с диаметром АВ без точек отрезка AB.

3.Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде.

4.Центр окружности, описанной около прямоугольного треугольника — середина гипотенузы.

5. Касательная к окружности.Прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности.

1) Касательная перпендикулярна радиусу, проведенному в точку касания.

2) Если прямая l, проходящая через точку на окружности, перпендикулярна радиусу, проведенному в эту точку, то прямая l — касательная к окружности.

3) Если прямые, проходящие через точку M, касаются окружности в точках A и B, то MA=MB (Касательные, проведенные к окружности из одной точки, равны).

4) Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

5) Теорема о биссектрисах треугольника.Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.

6.Радиус окружности, вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c, равен .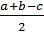

7.Если M — точка касания со стороной AC окружности, вписанной в треугольник ABC, то AM=p−BC, где p — полупериметр треугольника.

8.Окружность касается стороны BC треугольника ABC и продолжений сторон AB и AC. Тогда расстояние от вершины A до точки касания окружности с прямой AB равно полупериметру треугольника ABC.

9.Окружность, вписанная в треугольник ABC, касается сторон AB, BC и AC соответственно в точках K, L и M. Если ÐBAC = α, то ÐKLM = 90 0 − .

10.Даны окружности радиусов r и R (R > r). Расстояние между их центрами равно a (a>R + r). Тогда отрезки общих внешних и общих внутренних касательных, заключенные между точками касания, равны соответственно a 2 −(R−r) 2 и a 2 −(R+r) 2 .

11.Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.

12. Касающиеся окружности.Говорят, что две окружности касаются, если они имеют единственную общую точку (точка касания).

1) Точка касания двух окружностей лежит на их линии центров.

2) Окружности радиусов rиRс центрами O₁ и O₂ касаются внешним образом тогда и только тогда, когда R + r = O₁O₂.