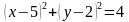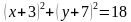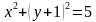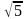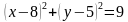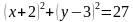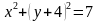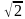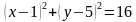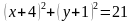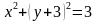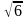Уравнение окружности и прямой 9 класс геометрия самостоятельная с ответами

Работа содержит 2 варианта по 7 заданий .

Видео:Уравнение окружности (1)Скачать

Скачать:

Видео:УРАВНЕНИЯ ОКРУЖНОСТИ И ПРЯМОЙ 9 класс геометрияСкачать

Предварительный просмотр:

Самостоятельная работа « Уравнение окружности и прямой»

1) Определите координаты центра окружности и её радиус по заданному уравнению. Начертите заданную окружность в системе координат

2) а) Принадлежит ли точка К(2;-1) окружности , заданной уравнением х² + (у+4)²=25

б) Принадлежит ли точка Р (- 3;-1) прямой заданной уравнением

3 ) Найдите координаты точек пересечения прямой , заданной уравнением -3х+4у-12 =0 с осями координат.

4) Прямая, заданная уравнением αх — 5у +9 = 0, проходит через точку М(2;3). Найдите число α.

5) Напишите уравнение окружности с центром С(-3;2), если эта окружность проходит через точку А(1;4)

6) Напишите уравнение прямой, проходящей через точки А( -2;-1) и В(3;1)

7) Прямая проходит через точки А (1; -1) и В (-3;2). Найдите площадь треугольника, ограниченного этой прямой и осями координат.

Самостоятельная работа « Уравнение окружности и прямой»

1) Определите координаты центра окружности и её радиус по заданному уравнению. Начертите заданную окружность в системе координат

а) б)

2) а) Принадлежит ли точка К(2;-1) окружности , заданной уравнением х² + (у-1)²=8

б) Принадлежит ли точка Р (- 3;-1) прямой заданной уравнением

3) Найдите координаты точек пересечения прямой , заданной уравнением 2х — 3у-12 =0 с осями координат.

4) Прямая , заданная уравнением 4х +bу — 6 = 0, проходит через точку N(3;2). Найдите число b.

5 ) Напишите уравнение окружности с центром С(-2;-1), если эта окружность проходит через точку А(1;3)

6) Напишите уравнение прямой, проходящей через точки А( 3;-2) и

7) Прямая проходит через точки А (-2; -1) и В (1;1). Найдите площадь треугольника, ограниченного этой прямой и осями координат.

Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

По теме: методические разработки, презентации и конспекты

Проверочная работа по геометрии в 9 классе на тему «Уравнения окружности и прямой)

Работа состоит из 8 вариантов по теме «Уравнения окружности и прямой».

6 класс. Задания для подготовки к проверочным работа по теме «Пропорции. Длина окружности и площадь круга»

Материал предназначен для родителей для того, чтобы они могли проконтролировать подготовку детей к различным проверочным работам.

Проверочная работа на тему «Прямая и косвенная речь»

Данную работу можно использовать для проверки усвоения темы «Прямая и косвенная речь» .

Проверочная работа.Тема: точка. Прямая. Расположение точек на прямой. Отрезок. Измерение отрезков.

Проверочная работа.Тема: точка. Прямая. Расположение точек на прямой. Отрезок. Измерение отрезков.

Проверочная работа по теме «Прямая речь» 5 класс

Проверочная работа по теме «Прямая речь» 5 класс.

Проверочная работа по теме «Прямая и косвенная речь. Диалог. Цитирование» 8 класс

Проверочная работа для 8 класса по теме «Прямая и косвенная речь. Диалог. Цитирование» по программе М. Разумовской.

Проверочная работа по теме «Прямая и косвенная речь»

Мини-тест для 8 класса по теме «Прямая и косвенная речь&quot.

Видео:Геометрия 9 класс (Урок№9 - Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой.)Скачать

Самостоятельная работа по геометрии «Уравнение окружности, прямой» 9 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Самостоятельная работа «Уравнение окружности и прямой»

Запишите уравнение окружности с центром в точке М и радиусом R, где М(-3;2) и R=2. Проходит ли данная окружность через точку D(-3;4)?

Запишите уравнение прямой CD, если С(-3;1) и D (-5;9)

Найдите координаты точки пересечения двух прямых -3х-у+1=0 и 4х+3у+7=0.

Прямая задана уравнением 4х+3у-24=0.

а)найдите координаты точек А и В пересечения прямой с осями координат;

б) найдите координаты середины отрезка АВ;

в) найдите длину отрезка АВ.

5 . Прямая у=х+4 и у=-2х+1 пересекаются в точке О.

а) найдите координаты точки О;

б) запишите уравнение окружности с центром в точке О, которая проходит через точку

Самостоятельная работа «Уравнение окружности и прямой»

1 . Запишите уравнение окружности с центром в точке М и радиусом R, где М(2;-1) и R=3. Проходит ли данная окружность через точку С(2;2)?

Запишите уравнение прямой АВ, если А(-3;4) и В (-1;-2).

Найдите координаты точки пересечения двух прямых -2х-7у+1=0 и 3х+4у+5=0.

Прямая задана уравнением 3х+2у-12=0. Найдите:

а) координаты точек А и В пересечения прямой с осями координат;

б) найдите координаты середины отрезка АВ;

в) найдите длину отрезка АВ.

5 . Прямая у=х+4 и у=-2х-5 пересекаются в точке О.

а) найдите координаты точки О;

б) запишите уравнение окружности с центром в точке О, которая проходит через точку

а) произвольный треугольник и найти его площадь;

б) прямоугольный треугольник и найти его площадь;

в) трапецию и найти её площадь. ( 3 б. )

2 . Найдите гипотенузу прямоугольного треугольника с катетами 5 см и 12 см. (2 б.)

3. Найдите площадь и периметр прямоугольника, если его диагональ равна 10 см, а одна из сторон 6 см. (4 б.)

4 . Найдите площадь треугольника со сторонами 12 см, 35 см и 37 см. (2 б.)

« 3 » — 3 – 5 баллов

« 4 » — 6 – 9 баллов

« 5 » — 10 – 11 баллов

а) произвольный треугольник и найти его площадь;

б) прямоугольный треугольник и найти его площадь;

в) трапецию и найти её площадь . ( 3 б. )

2 . Найдите катет прямоугольного треугольника с гипотенузой 13 см и катетом 12 см. (2 б.)

3. Найдите площадь и периметр ромба с диагоналями 12 см и 16 см. (4 б.)

4 . Найдите площадь треугольника со сторонами 9 см, 40 см и 41 см. (2 б.)

« 3 » — 3 – 5 баллов

« 4 » — 6 – 9 баллов

« 5 » — 10 – 11 баллов

а) произвольный треугольник и найти его площадь;

б) прямоугольный треугольник и найти его площадь;

в) трапецию и найти её площадь. ( 3 б. )

2 . Найдите гипотенузу прямоугольного треугольника с катетами 5 см и 12 см. (2 б.)

3. Найдите площадь и периметр прямоугольника, если его диагональ равна 10 см, а одна из сторон 6 см. (4 б.)

4 . Найдите площадь треугольника со сторонами 12 см, 35 см и 37 см. (2 б.)

« 3 » — 3 – 5 баллов

« 4 » — 6 – 9 баллов

« 5 » — 10 – 11 баллов

а) произвольный треугольник и найти его площадь;

б) прямоугольный треугольник и найти его площадь;

в) трапецию и найти её площадь. ( 3 б. )

2 . Найдите высоту треугольника с высотой 13 см, если его площадь равна 16,9 см 2 .

2 . Найдите катет прямоугольного треугольника с гипотенузой 13 см и катетом 12 см. (2 б.)

3. Найдите площадь и периметр ромба с диагоналями 12 см и 16 см. (4 б.)

4 . Найдите площадь треугольника со сторонами 9 см, 40 см и 41 см. (2 б.)

« 3 » — 3 – 5 баллов

« 4 » — 6 – 9 баллов

« 5 » — 10 – 11 баллов

а) произвольный треугольник и найти его площадь;

б) прямоугольный треугольник и найти его площадь;

в) трапецию и найти её площадь. ( 3 б. )

2 . Найдите гипотенузу прямоугольного треугольника с катетами 5 см и 12 см. (2 б.)

3. Найдите площадь и периметр прямоугольника, если его диагональ равна 10 см, а одна из сторон 6 см. (4 б.)

4 . Найдите площадь треугольника со сторонами 12 см, 35 см и 37 см. (2 б.)

« 3 » — 3 – 5 баллов

« 4 » — 6 – 9 баллов

« 5 » — 10 – 11 баллов

а) произвольный треугольник и найти его площадь;

б) прямоугольный треугольник и найти его площадь;

в) трапецию и найти её площадь. ( 3 б. )

2 . Найдите катет прямоугольного треугольника с гипотенузой 13 см и катетом 12 см. (2 б.)

3. Найдите площадь и периметр ромба с диагоналями 12 см и 16 см. (4 б.)

4 . Найдите площадь треугольника со сторонами 9 см, 40 см и 41 см. (2 б.)

« 3 » — 3 – 5 баллов

« 4 » — 6 – 9 баллов

« 5 » — 10 – 11 баллов

Контрольная работа по теме «Площадь»

а) гипотенузу прямоугольного треугольника с катетами 6 см и 8 см;

б) высоту, проведённую к гипотенузе. ( 3 б. ).

2 . Докажите, что треугольник со сторонами 12 см, 35 см и 37 см является прямоугольным. (2 б.)

3 . Диагонали ромба равны 8 см и 6 см. Найдите периметр и площадь ромба. (3 б.)

4. Стороны параллелограмма 12 см и 9 см, а его площадь 36 см 2 . Найдите высоты параллелограмма . (3 б.)

5 . В прямоугольной трапеции основания равны 6 см и 9 см, а большая боковая сторона равна 5 см. Найти площадь трапеции. ( 3 б. )

6. Высота, проведённая из вершины тупого угла прямоугольной трапеции, отсекает квадрат, площадь которого равна 16 см 2 . Найдите площадь трапеции, если её тупой угол равен 135 0 .( 4 б. )

« 3 » — 5 – 8 баллов

« 4 » — 9 – 15 баллов

« 5 » — 16 – 18 баллов

Контрольная работа по теме «Площадь»

а) катет прямоугольного треугольника с гипотенузой 13 см и вторым катетом 12 см;

б) высоту, проведённую к гипотенузе. ( 3 б. ).

2 . Докажите, что треугольник со сторонами 9 см, 40 см и 41 см является прямоугольным. (2 б.)

3 . Диагонали ромба равны 12 см и 16 см. Найдите периметр и площадь ромба. (3 б.)

4. Высоты параллелограмма 2 см и 6 см, а его площадь 48 см 2 . Найдите стороны параллелограмма. (3 б.)

5 . В равнобедренной трапеции основания равны 6 см и 14 см, а боковая сторона равна 5 см. Найти площадь трапеции. ( 3 б. )

6. Высота, проведённая из вершины тупого угла прямоугольной трапеции, отсекает квадрат, площадь которого равна 36 см 2 . Найдите площадь трапеции, если её острый угол равен 45 0 .( 4 б. )

« 3 » — 5 – 8 баллов

« 4 » — 9 – 15 баллов

« 5 » — 16 – 18 баллов

КонтРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ ТЕМА: ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ. ТЕТРАЭДР И ПАРАЛЛЕЛЕПИПЕД.

1. Прямые m и n лежат в параллельных плоскостях α и β. Могут ли эти прямые быть:

Сделайте рисунок для каждого возможного случая.

2. Рассмотрим тетраэдр DABC. Построить сечение, проходящее через точки M, N, Р.

3 . Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей

через точки F, R и G, являющиеся серединами ребер АВ, ВС и DD1.

4. Даны параллельные плоскости α и β, их пересекают две параллельные прямые a и b в точках А1,

А2, В1, В2 соответственно. Найти градусную меру угла А1А2В2, если угол А1В1В2 равен 110 0 .

5. Через точку M, лежащую между параллельными плоскостями α и β, проведены прямые a и b.

Прямая a пересекает плоскости α и β в точках А1 и А2 соответственно, прямая b – в точках В1 и

В2. Найдите длину отрезка А1В1, если А2В2 = 12 см, В1О : ОВ2 = 3 : 4.

1 . Прямые m и n лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть:

Сделайте рисунок для каждого возможного случая.

2. Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Построить сечение, проходящее

через точки M, N, L.

3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки F и R,

являющиеся серединами ребер DC и BC, и точку G, такую, что G ϵ DA, АG : GD = 1 : 3.

4. Даны параллельные плоскости α и β, их пересекают две параллельные прямые a и b в точках А1,

А2, В1, В2 соответственно. Найти градусную меру угла А2А1В1, если угол В1В2А2 равен 60 0 .

5. Через точку M, не лежащую между параллельными плоскостями α и β, проведены прямые a и

b. Прямая a пересекает плоскости α и β в точках А1 и А2 соответственно, прямая b – в точках В1

и В2. Найдите длину отрезка А2В2, если А1В1= 15 см, МВ1 : МВ2 = 3 : 5.

Самостоятельная работа 9 класс

Найдите координаты вектора АВ, зная координаты его начала и конца:

а) А (2;7), В(-2;7), б) А (9;0), В (0;-6)

Найдите длину вектора: а) а , б) в

Начертите окружность, заданную уравнением: х 2 +у 2 =4

Напишите уравнение окружности радиуса r с центром А, если А(0,6); r=1/2

Напишите уравнение окружности, проходящей через точку А(-4,0) с центром в В (0,8).

Найдите координаты вектора АВ, зная координаты его начала и конца:

а) А (-2;7), В(2;7), б) А (3;0), В (0;-2)

Найдите длину вектора: а) а , б) в

Начертите окружность, заданную уравнением: х 2 +у 2 =16

Напишите уравнение окружности радиуса r с центром А, если А(0,6); r=5

Напишите уравнение окружности, проходящей через точку А(-9,0) с центров в В (0,2).

Найдите координаты вектора АВ, зная координаты его начала и конца:

а) А (2;7), В(-2;7), б) А (9;0), В (0;-6)

Найдите длину вектора: а) а , б) в

Начертите окружность, заданную уравнением: х 2 +у 2 =4

Напишите уравнение окружности радиуса r с центром А, если А(0,6); r=1/2

Напишите уравнение окружности, проходящей через точку А(-4,0) с центром в В (0,8).

Найдите координаты вектора АВ, зная координаты его начала и конца:

а) А (-2;7), В(2;7), б) А (3;0), В (0;-2)

Найдите длину вектора: а) а , б) в

Начертите окружность, заданную уравнением: х 2 +у 2 =16

Напишите уравнение окружности радиуса r с центром А, если А(0,6); r=5

Напишите уравнение окружности, проходящей через точку А(-9,0) с центров в В (0,2).

Самостоятельная работа по теме

«Площадь прямоугольника, квадрата, параллелограмма»

1 . Найдите площадь прямоугольника, если его периметр равен 144 см, а стороны относятся как 5:7. (3 б.)

2. В прямоугольнике одна сторона в 3 раза больше другой, а площадь равна 48 см 2 . Найдите площадь квадрата построенного на большей стороне прямоугольника. (3 б. )

3. Площади квадратов, построенных на сторонах прямоугольника равны 49 см 2 . и 144 см 2 . Найдите периметр прямоугольника. (3 б.)

4. Стороны параллелограмма 8 см и 14 см, а один из углов равен 30 0 . Найдите площадь параллелограмма. (3 б.)

5. Сторона параллелограмма равна 16 см, а высота, проведённая к ней равна 9 см. Найти периметр параллелограмма, если высота, проведённая к смежной стороне равна 12 см.

6. В параллелограмме:

а) сторона равна 26,5 см, а высота, проведённая к ней – 8 см. Найти площадь параллелограмма;

б) площадь равна 255 см 2 , а сторона — 15 см. Найти высоту, проведённую к этой стороне. (3б.)

« 3 » — 3 — 7 баллов

« 4 » — 8 – 11 баллов

« 5 » — 12 – 15 баллов

16 баллов и более – дополнительная отметка.

Самостоятельная работа по теме

«Площадь прямоугольника, квадрата, параллелограмма»

1 . Найдите площадь прямоугольника, если его периметр равен 74 см, а одна из сторон на 17 см больше другой. (3 б.)

2. В прямоугольнике одна сторона в 4 раза больше другой, а площадь равна 36 см 2 . Найдите площадь квадрата построенного на меньшей стороне прямоугольника. (3 б. )

3. Площади квадратов, построенных на сторонах прямоугольника равны 64 см 2 . и 121 см 2 . Найдите площадь прямоугольника. (3 б.)

4. Стороны параллелограмма 10 см и 12 см, а один из углов равен 30 0 . Найдите площадь параллелограмма. (3 б.)

5. Сторона параллелограмма равна 18 см, а высота, проведённая к ней равна 8 см. Найти периметр параллелограмма, если высота, проведённая к смежной стороне равна 9 см.

6. В параллелограмме:

а) сторона равна 18,5 см, а высота, проведённая к ней – 6 см. Найти площадь параллелограмма;

б) площадь равна 315 см 2 , а сторона — 9 см. Найти высоту, проведённую к этой стороне. (3б.)

« 3 » — 3 — 7 баллов

« 4 » — 8 – 11 баллов

« 5 » — 12 – 15 баллов

16 баллов и более – дополнительная отметка.

Контрольная работа по теме

«Векторы. Метод координат»

а) Найдите координаты середины отрезка АВ.

б) Найдите длину отрезка АВ.

в) Определите, какая из данных точек принадлежит прямой х — у + 4 = 0;

г) Найти координаты вектора АВ (4 б.)

2. Составьте уравнение прямой АВ, если А(-2;1), В(2;5). (3 б. )

3. Найти координаты точек пересечения прямой 3х + 2у – 12 = 0 с осями координат. (2 б.)

4. Найти координаты точки пересечения прямых 2х + 3у – 10 = 0 и х – 2у + 9 = 0. (2 б.)

5. Даны точки А(-2;1), В(2;5), С(4;1). Для треугольника АВС составьте уравнение медианы В D . (4 б.)

« 4 » — 9 – 12 баллов

« 5 » — 13 – 15 баллов

Контрольная работа по теме

«Векторы. Метод координат»

1 . Даны точки А( 4 ; 8 ), В(2; -2 ).

а) Найдите координаты середины отрезка АВ.

б) Найдите длину отрезка АВ.

в) Определите, какая из данных точек принадлежит прямой х — у + 4 = 0;

г) Найти координаты вектора АВ. (4 б.)

2. Составьте уравнение прямой АВ, если А(-2;1), В(4;1). (3 б. )

3. Найти координаты точек пересечения прямой 2 х — 5у + 20 = 0 с осями координат. (2 б.)

4. Найти координаты точки пересечения прямых х + 2у – 5 = 0 и 3 х – у — 8 = 0. (2 б.)

5. Даны точки А(-2;1), В(2;5), С(4;1). Для треугольника АВС составьте уравнение медианы СК . (4 б.)

« 4 » — 9 – 12 баллов

« 5 » — 13 – 15 баллов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 988 человек из 78 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 673 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 68 регионов

Ищем педагогов в команду «Инфоурок»

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 539 383 материала в базе

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 20.01.2018
• 781
• 0

• 20.01.2018
• 560
• 5

• 20.01.2018
• 1002
• 0

• 20.01.2018
• 8507
• 45

• 20.01.2018
• 1426
• 11

• 20.01.2018
• 1585
• 146

• 20.01.2018
• 303
• 0

• 20.01.2018
• 1104
• 17

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 20.01.2018 18373
• DOCX 53 кбайт
• 539 скачиваний
• Рейтинг: 4 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Нещерет Елена Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет
• Подписчики: 1
• Всего просмотров: 108201
• Всего материалов: 21

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Уравнение окружности. Практика. Урок 7. Геометрия 9 классСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России классы будут переводить на дистант, если заболели 20% детей

Время чтения: 1 минута

Ученики 5-11 классов Воронежа перейдут на дистанционное обучение с 3 февраля

Время чтения: 1 минута

В Оренбурге продлили дистанционное обучение для школьников

Время чтения: 1 минута

Володин призвал выработать единые нормы организации групп продленного дня

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:ДЕКАРТОВЫ КООРДИНАТЫ. Контрольная № 3 Геометрия 9 класс.Скачать

Уравнение окружности. Самостоятельная работа. 9 класс

Просмотр содержимого документа
«Уравнение окружности. Самостоятельная работа. 9 класс»

1. Определить координаты центра и радиус окружности, заданной уравнением:

а)

б)

в)

2. Запишите уравнение окружности с центром в точке А и радиусом r

б) А(–5; 0) и r=

3. Запишите уравнение окружности, проходящей через точку D(-7; 2), и центром в точке О(-5;-3)

1. Определить координаты центра и радиус окружности, заданной уравнением:

а)

б)

в)

2. Запишите уравнение окружности с центром в точке А и радиусом r

б) А(–2; 0) и r=

3. Запишите уравнение окружности, проходящей через точку D(-4; 1), и центром в точке О(0;-2)

1. Определить координаты центра и радиус окружности, заданной уравнением:

а)

б)

в)

2. Запишите уравнение окружности с центром в точке А и радиусом r

б) А(9; 0) и r=

3. Запишите уравнение окружности, проходящей через точку D(-5; 1), и центром в точке О(-4;6)

1. Определить координаты центра и радиус окружности, заданной уравнением:

а)

б)

в)

2. Запишите уравнение окружности с центром в точке А и радиусом r

б) А(0; –2) и r=

3. Запишите уравнение окружности, проходящей через точку D(6; -2), и центром в точке О(-1;-3)

1. Определить координаты центра и радиус окружности, заданной уравнением:

а)

б)

в)

2. Запишите уравнение окружности с центром в точке А и радиусом r

б) А(–5; 0) и r=

3. Запишите уравнение окружности, проходящей через точку D(-7; 2), и центром в точке О(-5;-3)

1. Определить координаты центра и радиус окружности, заданной уравнением:

а)

б)

в)

2. Запишите уравнение окружности с центром в точке А и радиусом r

б) А(–2; 0) и r=

3. Запишите уравнение окружности, проходящей через точку D(-4; 1), и центром в точке О(0;-2)

1. Определить координаты центра и радиус окружности, заданной уравнением:

а)

б)

в)

2. Запишите уравнение окружности с центром в точке А и радиусом r

б) А(9; 0) и r=

3. Запишите уравнение окружности, проходящей через точку D(-5; 1), и центром в точке О(-4;6)

1. Определить координаты центра и радиус окружности, заданной уравнением:

а)

б)

в)

2. Запишите уравнение окружности с центром в точке А и радиусом r

б) А(0; –2) и r=

3. Запишите уравнение окружности, проходящей через точку D(6; -2), и центром в точке О(-1;-3)

🔥 Видео

Уравнение окружности | Геометрия 7-9 класс #90| ИнфоурокСкачать

Уравнение прямой. Видеоурок 6. Геометрия 9 классСкачать

9 класс, 7 урок, Уравнение прямойСкачать

9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

Разбор всех типов задания №6 из ОГЭ по математике 2024Скачать

Как проверяют учеников перед ЕНТСкачать

Уравнение окружностиСкачать

Уравнение прямой. Урок 6. Геометрия 9 классСкачать

Алгебра с нуля до ОГЭ | Математика ОГЭ 2023 | УмскулСкачать

УРАВНЕНИЕ ОКРУЖНОСТИ 8 и 9 класс геометрияСкачать

УРАВНЕНИЕ ОКРУЖНОСТИСкачать

№969. Напишите уравнение окружности с диаметром MN, если: а) М (-3; 5),Скачать