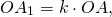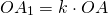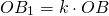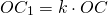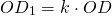Гомотетия четырехугольника с коэффициентом 2 (4 видео)

Свойства, типы и примеры гомотетии

homotecia представляет собой геометрическое изменение в плоскости, где расстояния от фиксированной точки, называемой центром (O), умножаются на общий коэффициент. Таким образом, каждая точка P соответствует другой точке P ‘, являющейся произведением преобразования, и они выровнены с точкой O.

Тогда гомотетия — это соответствие между двумя геометрическими фигурами, где преобразованные точки называются гомотетическими, и они выровнены с фиксированной точкой и сегментами, параллельными друг другу..

1 гомотеция
2 свойства
3 типа
- 3.1 Прямая гомотетия
- 3.2 Обратная гомотетия
4 Композиция
5 примеров
- 5.1 Первый пример
- 5.2 Второй пример
6 Ссылки

Содержание

homotecia
свойства
Гомотетия
Гомотетия, свойства гомотетии
Свойства гомотетии
🔍 Видео

Видео:Гомотетия. Коэффициент гомотетии. Центр гомотетии. Гомотетичные фигуры. Геометрия 8-9 классСкачать

homotecia

Гомотетия — это преобразование, которое не имеет конгруэнтного изображения, потому что из рисунка будет получена одна или несколько фигур большего или меньшего размера, чем исходная фигура; то есть гомотетия превращает многоугольник в другой подобный.

Чтобы гомотетия была выполнена, они должны соответствовать точка-точка и прямая-прямая, чтобы пары гомологичных точек были выровнены с третьей фиксированной точкой, которая является центром гомотетии..

Аналогично, пары линий, которые соединяют их, должны быть параллельными. Соотношение между такими сегментами является константой, называемой коэффициентом гомотетии (k); таким образом, что гомотетия может быть определена как:

Чтобы сделать этот тип преобразования, вы начинаете с выбора произвольной точки, которая будет центром гомотетии..

С этой точки отрезки линий рисуются для каждой вершины фигуры, которая должна быть преобразована. Масштаб, в котором выполняется воспроизведение нового рисунка, определяется по причине гомотетии (k)..

Видео:ГомотетияСкачать

свойства

Одним из основных свойств гомотетии является то, что по причине гомотетии (k) все гомотетические фигуры схожи. Среди других выдающихся свойств являются следующие:

— Центр гомотетии (O) — единственная двойная точка, и она превращается в себя; то есть не меняется.

— Линии, проходящие через центр, трансформируются (они двойные), но точки, составляющие его, не являются двойными.

— Прямые, которые не проходят через центр, превращаются в параллельные линии; таким образом, углы гомотетии остаются неизменными.

— Образ сегмента с помощью гомотетии центра O и отношения k представляет собой отрезок, параллельный этому, и имеет k-кратную длину. Например, как видно на следующем изображении, сегмент AB с помощью гомотетики приведет к другому сегменту A’B ‘, так что AB будет параллельным A’B’, а k будет:

— Гомотетические углы конгруэнтны; то есть они имеют одинаковую меру. Следовательно, изображение угла — это угол, имеющий одинаковую амплитуду..

С другой стороны, гомотетия варьируется в зависимости от значения ее отношения (k), и могут возникнуть следующие случаи:

— Если константа k = 1, все точки фиксированы, потому что они трансформируются. Таким образом, гомотетическая фигура совпадает с оригиналом и преобразование будет называться тождественной функцией.

— Если k ≠ 1, единственной фиксированной точкой будет центр гомотетии (O).

— Если k = -1, гомотетия становится центральной симметрией (C); то есть вращение вокруг C будет происходить под углом 180 или .

— Если k> 1, размер преобразованного рисунка будет больше размера исходного.

— Да 0 0; то есть гомотетические точки находятся на одной стороне относительно центра:

Коэффициент пропорциональности или отношения сходства между прямыми гомотетическими фигурами всегда будет положительным.

Видео:9 класс. Геометрия. Гомотетия.Скачать

Гомотетия

Гомотетия — это преобразование, при котором каждой точке A ставится в соответствие точка A1, лежащая на прямой OA, по правилу

где k — постоянное, отличное от нуля число, O — фиксированная точка.

Точка O называется центром гомотетии, число k — коэффициентом гомотетии.

гомотетия с коэффициентом k>0

Чтобы построить четырёхугольник, гомотетичный 4-угольнику ABCD с центром гомотетии в точке O и коэффициентом k, k>0, нужно провести лучи с началом в точке O, проходящие через вершины A, B, C, D, отложить на них отрезки соответствующей длины:

и соединить вершины A1, B1, C1и D1 отрезками.

При k

и соединить вершины A1, B1, C1 отрезками.

При гомотетии с коэффициентом k=1 каждая точка переводится сама в себя.

При k= -1 гомотетия является симметрией относительно центра O (то есть центральная симметрия является частным случаем гомотетии).

Гомотетия есть преобразование подобия. Следовательно, гомотетия обладает свойствами подобия.

Свойства преобразования гомотетии

1) При гомотетии прямые переходят в прямые, полупрямые- в полупрямые, отрезки — в отрезки, углы — в углы.

2) Сохраняются углы между полупрямыми (соответственно, сохраняется параллельность прямых).

Стороны гомотетичных фигур пропорциональны. а углы — равны.

Видео:гомотетияСкачать

Гомотетия, свойства гомотетии

Правило

Гомотетия с коэффициентом k > 0 и центром в точке О — преобразование фигуры F в фигуру F₁, при котором каждая ее точка X переходит в точку X₁, такую, что вектор OX₁ = k • OX.

Видео:Гомотетия преобразование подобия. Свойства преобразования подобия. Геометрия 8-9 классСкачать

Свойства гомотетии

Свойства
1. Гомотетия является преобразованием подобия.

2. Гомотетия переводит прямую в прямую, отрезок — в отрезок.

3. Гомотетия (k > 0) переводит луч в сонаправленный луч.

4. Гомотетия сохраняет углы.

5. При k ? 1 гомотетия переводит прямую, не проходящую через центр гомотетии О, в параллельную прямую, отрезок — в параллельный отрезок. Прямые, проходящие через центр гомотетии, отображаются на себя.

6. Гомотетия переводит окружность в окружность.

7. Преобразование. обратное гомотетии с коэффициентом k ? 0, есть гомотетия с тем же центром гомотетии О и коэффициентом гомотетии 1 k .

8. Композиции двух гомотетий с общим коэффициентом О и коэффициентами k₁ и k₂ есть гомотетия с тем же центром О и коэффициентом k = k₁ • k₂.