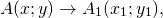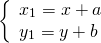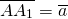Перенос треугольника на вектор (5 видео)

Параллельный перенос

Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.

Строгое определение параллельного переноса даётся либо через декартовы координаты, либо через вектор.

1) Введём на плоскости декартовы координаты x, y.

Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F.

Формулы параллельного переноса

Если при параллельном переносе точка A(x;y) переходит в точку A1(x1;y1)

то параллельный перенос задаётся формулами:

Говорят также, что A1 является образом точки A при параллельном переносе на вектор (a; b). Точка A называется прообразом.

2) Параллельный перенос на данный вектор ā называется отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, то вектор AA1 равен вектору ā:

Свойства параллельного переноса

1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние).

2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).

4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1.

В алгебре параллельный перенос широко используется для построения графиков функций.

Содержание

Параллельный перенос и поворот
Параллельный перенос
Поворот
Готовые работы на аналогичную тему
Примеры задач на параллельный перенос и поворот
§ 2. Параллельный перенос и поворот
Параллельный перенос
Поворот
Задачи
📺 Видео

Видео:Перенос треугольника по векторуСкачать

Параллельный перенос и поворот

Вы будете перенаправлены на Автор24

Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

Параллельный перенос

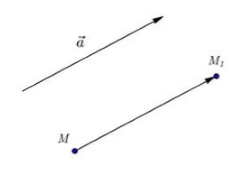
Введем определение параллельного переноса на вектор. Пусть нам дан вектор $overrightarrow$.

Рисунок 1. Параллельный перенос

Введем следующую теорему.

Параллельный перенос является движением.

Доказательство.

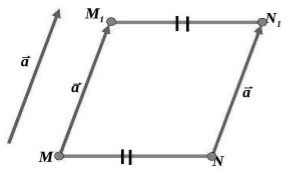
Пусть нам даны точки $M и N$. Пусть при их параллельном переносе на вектор $overrightarrow$ эти точки отображаются в точки $M_1$ и $N_1$, соответственно (рис. 2).

Рисунок 2. Иллюстрация теоремы 1

Значит четырехугольник $_1N_1N$ — параллелограмм и, следовательно, $MN=M_1N_1$. То есть параллельный перенос сохраняет расстояние между точками. Следовательно, параллельный перенос является движением.

Теорема доказана.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Поворот

Введем определение поворота вокруг точки $O$ на угол $alpha $.

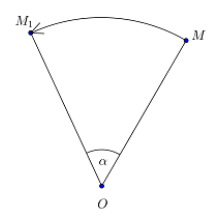
Поворот вокруг точки $O$ на угол $alpha $ — отображение плоскости на себя, при котором любая точка $M$ отображается на точку $M_1$ такую, что $_1=OM, angle M_1=angle alpha $ (Рис. 3).

Рисунок 3. Поворот

Готовые работы на аналогичную тему

Введем следующую теорему.

Поворот является движением.

Доказательство.

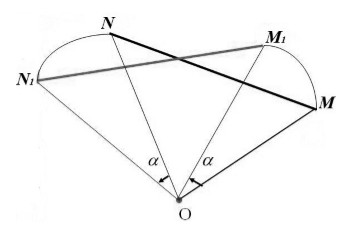
Пусть нам даны точки $M и N$. Пусть при их повороте вокруг точки $O$ на угол $alpha $ они отображаются в точки $M_1$ и $N_1$, соответственно (рис. 4).

Рисунок 4. Иллюстрация теоремы 2

Так как, по определению 2, $_1=OM, _1=ON$ и $overrightarrow<_1>=overrightarrow$, а ,$angle MON=angle M_1ON_1$, то

Следовательно, $MN=M_1N_1$. То есть поворот сохраняет расстояние между точками. Следовательно, поворот является движением.

Теорема доказана.

Видео:Скалярное произведение векторов. 9 класс.Скачать

Примеры задач на параллельный перенос и поворот

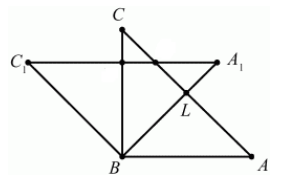
Построить треугольник $A_1B_1C_1$,образованный поворотом вокруг точки $B$ на угол $^0$ равнобедренного прямоугольного (с прямым углом $B)$ треугольника $ABC$.

Решение.

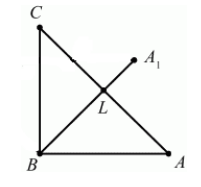
Очевидно, что точка $B$ перейдет сама в себя, то есть $B_1=B$. Так как поворот производится на угол, равный $^0$, а треугольник $ABC$ равнобедренный, то прямая $BA_1$ проходит через точку $L$ — середины стороны $AC$. По определению, отрезок $BA_1=BA$. Построим его (Рис. 5).

Построим теперь вершину $C_1$ по определению 2:

[angle CBC_1=^0, BC=BC_1]

Соединим все вершины треугольника $A_1B_1C_1$ (Рис. 6).

Решение закончено.

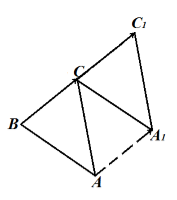
Построить параллельный перенос треугольника $ABC$ на вектор $overrightarrow$.

Решение.

Перенесем каждую вершину треугольника на вектор $overrightarrow$. Получаем треугольник $CA_1C_1$ (рис. 7).

Решение закончено.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 15 04 2021

Видео:#192 ПОВОРОТ И ПЕРЕНОС // ТРЕУГОЛЬНИКСкачать

§ 2. Параллельный перенос и поворот

Параллельный перенос

Пусть — данный вектор. Параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М₁, что вектор равен вектору (рис. 329).

Параллельный перенос является движением, т. е. отображением плоскости на себя, сохраняющим расстояния. Докажем это. Пусть при параллельном переносе на вектор точки М и N отображаются в точки М₁ и N₁ (см. рис. 329). Так как , то . Отсюда следует, что ММ₁ || NN₁ и MM₁ = NN₁, поэтому четырёхугольник MM₁N₁N — параллелограмм. Следовательно, MN = M₁N₁, т. е. расстояние между точками М и N равно расстоянию между точками М₁ и N₁ (случаи, когда точки М и N расположены на прямой, параллельной вектору , рассмотрите самостоятельно). Таким образом, параллельный перенос сохраняет расстояния между точками и поэтому представляет собой движение. Наглядно это движение можно представить себе как сдвиг всей плоскости в направлении данного вектора на его длину.

Поворот

Отметим на плоскости точку О (центр поворота) и зададим угол а (угол поворота). Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М₁, что ОМ = ОМ₁ и угол МОМ₁ равен α (рис. 330). При этом точка О остаётся на месте, т. е. отображается сама в себя, а все остальные точки поворачиваются вокруг точки О в одном и том же направлении — по часовой стрелке или против часовой стрелки. На рисунке 330 изображён поворот против часовой стрелки.

Поворот является движением, т. е. отображением плоскости на себя, сохраняющим расстояния.

Докажем это. Пусть О — центр поворота, α — угол поворота против часовой стрелки (случай поворота по часовой стрелке рассматривается аналогично). Допустим, что при этом повороте точки М и N отображаются в точки М₁ и N₁ (рис. 331). Треугольники OMN и ОМ₁N₁ равны по двум сторонам и углу между ними: ОМ = ОМ₁, ON = ON₁ и ∠MON = ∠M₁ON₁ (для случая, изображённого на рисунке 331, каждый из этих углов равен сумме угла α и угла M₁ON). Из равенства этих треугольников следует, что MN = M₁N₁, т. е. расстояние между точками М и N равно расстоянию между точками М, и N, (случай, когда точки О, М и N расположены на одной прямой, рассмотрите самостоятельно). Итак, поворот сохраняет расстояния между точками и поэтому представляет собой движение. Это движение можно представить себе как поворот всей плоскости вокруг данной точки О на данный угол α.

Задачи

1162. Начертите отрезок АВ и вектор . Постройте отрезок А1В1, который получается из отрезка АВ параллельным переносом на вектор .

1163. Начертите треугольник АВС, вектор , который не параллелен ни одной из сторон треугольника, и вектор , паралдельный стороне АС. Постройте треугольник А₁В₁С₁, который получается из треугольника АВС параллельным переносом: а) на вектор ; б) на вектор .

1164. Даны равнобедренный треугольник АВС с основанием АС и такая точка D на прямой АС, что точка С лежит на отрезке AD. а) Постройте отрезок BlD, который получается из отрезка ВС параллельным переносом на вектор . б) Докажите, что четырёхугольник ABB₁D — равнобедренная трапеция.

1165. Даны треугольник, трапеция и окружность. Постройте фигуры, которые получаются из этих фигур параллельным переносом на данный вектор .

1166. Постройте отрезок А₁В₁, который получается из данного отрезка АВ поворотом вокруг данного центра О: а) на 120° по часовой стрелке; б) на 75° против часовой стрелки; в) на 180°.

1167. Постройте треугольник, который получается из данного треугольника АВС поворотом вокруг точки А на угол 150° против часовой стрелки.

1168. Точка D является точкой пересечения биссектрис равностороннего треугольника АВС. Докажите, что при повороте вокруг точки D на угол 120° треугольник АВС отображается на себя.

1169. Докажите, что при повороте квадрата вокруг точки пересечения его диагоналей на угол 90° квадрат отображается на себя.

1170. Постройте окружность, которая получается из данной окружности с центром С поворотом вокруг точки О на угол 60° против часовой стрелки, если: а) точки О и С не совпадают; б) точки О и С совпадают.

1171. Постройте прямую а₁, которая получается из данной прямой а поворотом вокруг точки О на угол 60° по часовой стрелке, если прямая а: а) не проходит через точку О; б) проходит через точку О.

а) Построим окружность с центром О, которая касается прямой а (объясните, как это сделать). Пусть М — точка касания. При повороте вокруг точки О эта окружность отображается на себя, а касательная а отображается на некоторую касательную а₁ (объясните почему). Для построения прямой ах построим сначала точку М₁, в которую отображается точка М при повороте вокруг точки О на угол 60° по часовой стрелке, а затем проведём касательную а₁ к окружности в точке М₁.