Дано прямая а параллельна прямой б с секущая

Пусть прямая с пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы и , и — тоже вертикальные.

Углы и — смежные, это мы уже знаем. Сумма смежных углов равна .

Углы и (а также и , и , и ) — накрест лежащие. Накрест лежащие углы равны.

Углы и — односторонние. Они лежат по одну сторону от всей «конструкции». Углы и — тоже односторонние. Сумма односторонних углов равна , то есть

Углы и (а также и , и , и ) называются соответственными.

Соответственные углы равны, то есть

Углы и (а также и , и , и ) называют накрест лежащими.

Накрест лежащие углы равны, то есть

Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.

Ты нашел то, что искал? Поделись с друзьями!

1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении , считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен .

Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.

Пусть — биссектриса тупого угла . По условию, отрезки и равны и соответственно.

Рассмотрим углы и . Поскольку и параллельны, — секущая, углы и являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник — равнобедренный, следовательно, .

Периметр параллелограмма — это сумма всех его сторон, то есть

2. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.

Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: .

3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на чертеж. По условию, , то есть .

Углы и — односторонние при параллельных прямых и секущей, следовательно,

Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Даны параллельные прямые A и b c — секущая (угол)1 : (угол)2 = 5 : 7 Найдите все углы?

Даны параллельные прямые A и b c — секущая (угол)1 : (угол)2 = 5 : 7 Найдите все углы.

Угол1 = 180 : (5 + 7) * 5 = 75

угол2 = 180 : (5 + 7) * 7 = 105

угол8 = углу 1 = 75 как вертикальные

угол3 = углу 2 = 105 как накрест лежащие

угол7 = углу 3 = 105 как вертикальные

угол4 = углу 1 = 75 как накрест лежащие

угол5 = углу 4 = 75 как вертикальные

угол6 = углу 2 = 105как вертикальные

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Проведены две параллельные прямые bc и ah и их секущая ab?

Проведены две параллельные прямые bc и ah и их секущая ab.

Биссектриса угла ВАН пересекает вторую прямуюВС в точке С, угол АВС = 40 градусов.

Найдите угол АСВ.

Видео:№45. Прямая а параллельна стороне ВС параллелограмма ABCD и не лежит в плоскости параллелограмма.Скачать

Дано : а параллельно в, д — секущая, угол 1 = 43 см, найти угол 3?

Дано : а параллельно в, д — секущая, угол 1 = 43 см, найти угол 3.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Прямые A и B параллельны, C — секущая?

Прямые A и B параллельны, C — секущая.

Один из соответственных углов равен 30градусов .

Найдите остальные углы.

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Прямые M и N параллельны, с — секущая угол 3 плюс угол 6 равно 188 градусов Найдите градусные меры угол 1 угол 2 угол 3 Угол 4 угол 5 угол 6 угол с 7 угол 8?

Прямые M и N параллельны, с — секущая угол 3 плюс угол 6 равно 188 градусов Найдите градусные меры угол 1 угол 2 угол 3 Угол 4 угол 5 угол 6 угол с 7 угол 8.

Видео:№199. Прямая р параллельна стороне АВ треугольника ABC. Докажите, что прямые ВССкачать

Прямые b и d параллельны?

Прямые b и d параллельны.

Найдите угол 1 если угол 2 = 123°.

РЕШИТЕ ЧЕРЕЗ ДАНО!

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Прямые a и b параллельныНайдите угол 5 и угол 6, если угол 2 = 121°?

Прямые a и b параллельны

Найдите угол 5 и угол 6, если угол 2 = 121°.

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Помогите пожалуйстаПрямые а и Б параллельны С — секущая углы 1 и 2 внутренние односторонние И они относятся друг другу как 7÷8 найдите угол первый и второй?

Прямые а и Б параллельны С — секущая углы 1 и 2 внутренние односторонние И они относятся друг другу как 7÷8 найдите угол первый и второй.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Найдите все углы образованные при пересечении двух параллельных прямых секущей если один из этих углов равен 47 градуса?

Найдите все углы образованные при пересечении двух параллельных прямых секущей если один из этих углов равен 47 градуса.

Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Помогите срочно :углы образующие секущей параллельных прямых?

углы образующие секущей параллельных прямых.

Признаки параллельности прямых)).

Видео:№203. Найдите все углы, образованные при пересечении двух параллельных прямых а и b секущей сСкачать

Помогите решить :(даны две параллельные прямые?

(даны две параллельные прямые.

Угол 1 равен 120°.

Вы открыли страницу вопроса Даны параллельные прямые A и b c — секущая (угол)1 : (угол)2 = 5 : 7 Найдите все углы?. Он относится к категории Математика. Уровень сложности вопроса – для учащихся студенческий. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Математика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

В этом мы умножаем первым делом? Или делим? Ответ : умножение.

Первое действие всегда умножение.

1)972, 927, 729, 792, 279, 297 2)231, 213, 312, 321, 123, 132 3)177, 717, 771 4)903, 930, 309, 390 5)555.

Легко просто сделай например 972, 927, 729, 792, 297, 379.

X — первое число x — 0, 3 — второе число 1, 2x — третье число (x + x — 0, 3 + 1, 2x) = 4, 7 * 3 3, 2x — 0, 3 = 14, 1 3, 2x = 14, 1 + 0, 3 3, 2x = 14, 4 x = 14, 4 : 3, 2 x = 4, 5 первое число 4, 5 — 0, 3 = 4, 2 второе число 4, 5 * 1, 2 = 5, 4 третье ч..

Я очень люблю бабочек особенно разноцветных Когда мы с друзьями гуляем мы любим ловит бабочеу. Бабочки очень милые и красивые Вот я рассказала сочинение про бабаочек.

12см ^ 2 (или в чём там надо измерять).

— 5(2x + y) + 1, 5(3y — x) — 10x — 5y + 4, 5y — 1, 5x — 11, 5x — 0, 5y Подставляем значения Х и Y : — 115 — 5 = — 120.

Видео:Параллельные прямые (задачи).Скачать

Дано прямая а параллельна прямой б с секущая

305. Параллельны ли изображённые на рисунке 212 прямые a и b , если:

3) ∠ 4 = 125°, ∠ 6 = 55°;

4) ∠ 2 = 35°, ∠ 5 = 146°;

5) ∠ 1 = 98°, ∠ 6 = 82°;

6) ∠ 1 = 143°, ∠ 7 = 37°?

306. На каких из рисунков 213, а – г прямые m и n параллельны?

307. На рисунке 214 укажите все пары параллельных прямых.

308. На рисунке 215 укажите параллельные прямые, если ∠ 1 = 53°, ∠ 2 = 128°, ∠ 3 = 127°.

309. На рисунке 216 AB = BC , CD = DK . Докажите, что AB ‖ DK .

310. На рисунке 217 AK — биссектриса угла BAC , AM = MK . Докажите, что MK ‖ AC .

311. На рисунке 218 ∠ ACB = ∠ ACD , AD = CD . Докажите, что BC ‖ AD .

312. В треугольнике ABC известно, что AB = BC , ∠ A = 60°, ∠ BCD — смежный с ∠ ACB , CM — биссектриса угла BCD . Докажите, что AB ‖ CM .

313. Отрезки AB и CD пересекаются в точке O и делятся этой точкой пополам. Докажите, что AC ‖ BD .

314. На рисунке 219 AB = CD , BC = AD . Докажите, что AB ‖ CD .

315. Известно, что некоторая прямая m пересекает прямую a (рис. 220). Пересекает ли прямая m прямую b ?

316. Каково взаимное расположение прямых CD и EF на рисунке 221?

317. Угол ABC равен 60°, а угол BCD — 120°. Можно ли утверждать, что прямые AB и CD параллельны?

318. Угол между прямыми a и c равен углу между прямыми b и c . Можно ли утверждать, что прямые a и b параллельны?

319. Четыре угла, образованные при пересечении прямых a и b прямой c , равны по 40°, а любой из остальных четырёх углов — 140°. Можно ли утверждать, что прямые a и b параллельны?

320. Прямая пересекает биссектрису BM треугольника ABC в точке O , являющейся серединой отрезка BM , а сторону BC — в точке K . Докажите, что если OK ⊥ BM , то MK ‖ AB .

321. Отрезки AM и CK — медианы треугольника ABC . На продолжении отрезка AM за точку M отложен отрезок MF , а на продолжении отрезка CK за точку K — отрезок KD так, что MF = AM , KD = CK . Докажите, что точки B , D и F лежат на одной прямой.

Упражнения для повторения

322. Луч OC разбивает угол AOB на два угла так, что ∠ AOC : ∠ BOC = 3 : 5. Найдите угол между лучом OC и биссектрисой угла, смежного с углом AOB , если угол BOC на 42° больше угла AOC .

323. На рисунке 222 AB = BC , ∠ ABK = ∠ CBM . Докажите, что BM = BK .

324. Равнобедренные треугольники ABC и ADC имеют общее основание AC . Прямая BD пересекает отрезок AC в точке E . Докажите, что AE = EC .

Наблюдайте, рисуйте, конструируйте, фантазируйте

325. Приведите пример, когда общей частью (пересечением) треугольника и четырёхугольника является восьмиугольник.

Когда сделаны уроки

Пятый постулат Евклида

В § 6 вы узнали, что в качестве аксиом выбирают очевидные утверждения. Тогда почему бы, например, теоремы 1.1 и 5.1 не включить в список аксиом, ведь они тоже очевидны? Ответ на этот вопрос понятен: если какое-то утверждение можно доказать с помощью аксиом, то это утверждение — теорема, а не аксиома. С этих позиций очень поучительна история, связанная с пятым постулатом Евклида

V постулат. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними односторонние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны от секущей, с которой эта сумма меньше двух прямых углов ( рис. 223 ).

Можно показать, что пятый постулат и сформулированная нами в § 13 аксиома параллельности прямых равносильны, т. е. из постулата следует аксиома и наоборот — из аксиомы следует постулат.

Более двадцати веков многие учёные пытались доказать пятый постулат, т. е. вывести его из других аксиом Евклида. Лишь в начале XIX в. несколько математиков независимо друг от друга пришли к выводу: утверждение, что через данную точку, не лежащую на данной прямой, мож но провести только одну прямую, параллельную данной , является аксиомой.

Вам может показаться, что в этом выводе ничего особенного нет: присоединяем аксиому параллельности к уже существующему списку аксиом-правил, а дальше доказываем теоремы.

Однако если в футболе добавить только одно правило, например разрешить полевым игрокам играть и руками, то мы получим совершенно новую игру.

Если пятый постулат — это правило, которое мы принимаем, а не теорема, то его можно заменить противоположным утверждением.

Так и поступил Н.И. Лобачевский. Он заменил лишь одно правило — аксиому параллельности прямых — следующим: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную. Новая аксиома позволила построить новую геометрию — неевклидову.

Н.И. Лобачевский (1792–1856)

Выдающийся русский математик, про-

фессор Казанского университета.

С подобной идеей несколько позже выступил венгерский математик Янош Бойяи (1802–1860).

💥 Видео

Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

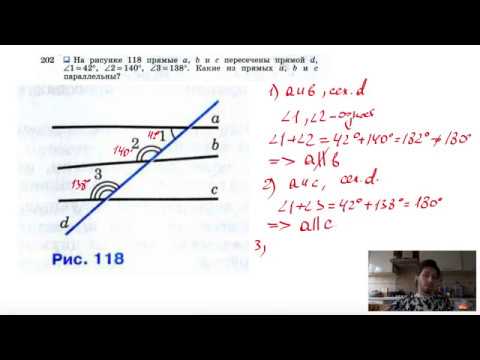
№202. На рисунке 116 прямые а, b и с пересечены прямой d, ∠1=42°, ∠2=140°, ∠3=138°. Какие из прямыхСкачать

10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

№92. Плоскость α и прямая a параллельны прямой b. Докажите, что прямая a либо параллельна плоскостиСкачать

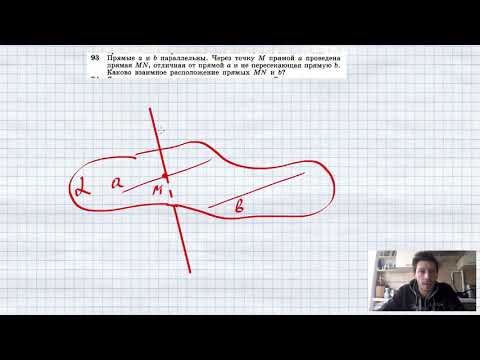
№93. Прямые а и b параллельны. Через точку М прямой a проведена прямая MN, отличная от прямой а и неСкачать

10 класс, 14 урок, Задачи на построение сеченийСкачать

Задачи на признаки параллельности прямых. Часть 1. Как кратко и грамотно оформить завершение задачи.Скачать

Свойства углов, образованных двумя параллельными прямыми и секущей Задачи на признаки параллельностСкачать