Лекция Способы задания векторов. Деление отрезка в заданном отношении. Скалярное произведение двух векторов и его основные свойства.

1.4. Способы задания векторов

Вектор может быть задан следующими способами:

1. Координатами вектора

2 . Координатами начальной z

и конечной точек.

3. Модулем вектора и углами , M

которые он образует с координатными осями.

При этом значения

называются направляющими косинусами . O y

Между этими способами задания a _z

векторов существует определённая связь. a _x

Например, переход от (2) к (1) x a _y

осуществляется следующим образом :

т ак как , то z A

Переход от (3) к (1) и наоборот

осуществляется по формулам: B

x O y

1.5. Деление отрезка в заданном отношении

Р ассмотрим следующую задачу : даны две точки и . Требуется найти точку такую, что отно-шение z А

Построим векторы : М

Из условия коллинеарности векторов

и имеем В

Полученное равенство представим в

координатной форме х Оу

(1)

Замечание 1. Из формул (1) следует частный случай деления отрезка пополам

П ример 1. Треугольник задан координатами своих вершин Найти его центр тяжести . z В

Известно, что центр тяжести треугольника

лежит на пересечении его медиан и, если

точка К  середина стороны ВС , то по А М К

свойству медиан у

Определим вначале координаты х С

точки К :

далее по формулам (1) получим координаты точки М :

Тема 2: Скалярное произведение

2.1. Скалярное произведение двух векторов и его основные свойства

Определение. Скалярным произведением двух векторов и называется число, равное произведению модулей этих векторов на косинус угла между ними и обозначается

(2)

Замечание 2. Формулу (2) можно представить в другой форме

(3)

Рассмотрим механический смысл скалярного произведения. Если  постоянная сила, а  вектор перемещения, то  работа силы на перемещении

Из определения скалярного произведения следуют его свойства:

1.  скалярное произведение коммутативно.

2. , если векторы и перпендикулярны (ортогональны), или хотя бы один из них является нулевым вектором.

Если воспользоваться замечанием 1 из лекции 4 и формулами (3), то легко доказать следующее свойство:

Таким образом, операции со скалярным произведением аналогичны операциям с многочленами.

2.2. Скалярное произведение векторов, заданных координатами

Из определения и свойства (1) скалярного произведения следуют формулы : .

Аналогично получаем :

(4)

2.3. Длина вектора. Угол между двумя векторами.

По формулам (2) и (4) получаем

(5)

Из определения скалярного произведения и формул (4), (5) следует

(6)

(7)

Если в формуле (7) положить , то найдем

Аналогично можно получить выражения для оставшихся двух направ-ляющих косинусов

; . (8)

Замечание 3. Формулу (5) для модуля вектора можно было получить, исходя из геометрического смысла координат вектора, используя теоре-му Пифагора.

Замечание 4. Из выражений (8) для направляющих косинусов следует их основное свойство

Пример 2. Даны два вектора Найти их скалярное произведение и угол между ними.

По формулам (5) и (7) получаем

Пример 3*. Найти координаты единичного вектора, который перпенди-кулярен вектору и образует угол с вектором

Из свойства направляющих косинусов следует, что координаты еди-ничного вектора равны значениям соответствующих направляющих косинусов и поэтому из условия задачи получаем следующую систему уравнений

Из второго уравнения системы получаем Тогда из первого уравнения имеем . Если полученные выражения подставить в третье уравнение системы, то приходим к квадратному уравнению

Из этого уравнения и . Тогда окончательно нахо-дим два единичных вектора , удовлетворяющих условию задачи.

Содержание

Деление отрезка в заданном соотношении: координаты точки
Определение координат точки, делящей отрезок в заданном отношении, на плоскости
Определение координат точки, делящей отрезок в заданном отношении, в пространстве
Урок 3
🎦 Видео

Видео:Деление отрезка в данном отношении. 11 класс.Скачать

Деление отрезка в заданном соотношении: координаты точки

Когда существуют условия деления отрезка в определенном отношении, необходимо уметь определять координаты точки, служащей разделителем. Выведем формулу для нахождения этих координат, поставив задачу на плоскости.

Видео:Деление отрезка в данном отношенииСкачать

Определение координат точки, делящей отрезок в заданном отношении, на плоскости

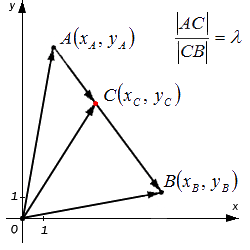
Исходные данные: задана прямоугольная система координат O x y и две лежащие на ней, несовпадающие точки с заданными координатами A ( x A , y A ) и B ( x B , y B ) . А также задана точка С , делящая отрезок А В в отношении λ (некоторое положительное действительное число). Необходимо определить координаты точки С : x C и y C .

Перед тем, как приступить к решению поставленной задачи, немного раскроем смысл заданного условия: «точка С , делящая отрезок А В в отношении λ ». Во-первых, это выражение свидетельствует о том, что точка С лежит на отрезке А В (т.е. между точками А и В ). Во-вторых, понятно, что согласно заданному условию отношение длин отрезков А С и С В равно λ . Т.е. верно равенство:

В этом случае точка А – начало отрезка, точка В – конец отрезка. Если бы было задано, что точка С делит в заданном отношении отрезок В А , тогда верным было бы равенство: .

Ну и совсем очевидный факт, что если λ = 1 , то точка С является серединой отрезка А В .

Решим поставленную задачу при помощи векторов. Отобразим произвольно в некой прямоугольной системе координат точки А , В и точку С на отрезке А В . Построим радиус-векторы указанных точек, а также векторы A C → и C B → . Согласно условиям задачи, точка С делит отрезок А В в отношении λ .

Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = ( x A , y A ) и O B → = ( x B , y B ) .

Определим координаты вектора : они будут равны координатам точки С , которые и требуется найти по условию задачи.

Используя операцию сложения векторов, запишем равенства: O C → = O A → + A C → O B → = O C → + C B → ⇔ C B → = O B → — O C →

По условию задачи точка С делит отрезок А В в отношении λ , т.е. верно равенство A C = λ · C B .

Векторы A C → и C B → лежат на одной прямой и являются сонаправленными. λ > 0 по условию задачи, тогда, согласно операции умножения вектора на число, получим: A C → = λ · C B → .

Преобразуем выражение, подставив в него : C B → = O B → — O C → .

A C → = λ · ( O B → — O C → ) .

Равенство O C → = O A → + A C → перепишем как O C → = O A → + λ · ( O B → — O C → ) .

Используя свойства операций над векторами, из последнего равенства следует: O C → = 1 1 + λ · ( O A → + λ · O B → ) .

Теперь нам остается непосредственно вычислить координаты вектора O C → = 1 1 + λ · O A → + λ · O B → .

Выполним необходимые действия над векторами O A → и O B → .

O A → = ( x A , y A ) и O B → = ( x B , y B ) , тогда O A → + λ · O B → = ( x A + λ · x B , y A + λ · y B ) .

Таким образом, O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ ) .

Резюмируя: координаты точки С , делящей отрезок А В в заданном отношении λ определяются по формулам : x C = x A + λ · x B 1 + λ и y C = у A + λ · y B 1 + λ .

Видео:Деление отрезка в данном отношении. 8 класс.Скачать

Определение координат точки, делящей отрезок в заданном отношении, в пространстве

Исходные данные: прямоугольная система координат O x y z , точки с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) .

Точка С делит отрезок А В в отношении λ . Необходимо определить координаты точки С .

Используем ту же схему рассуждений, что и в случае выше на плоскости, придем к равенству:

O C → = 1 1 + λ · ( O A → + λ · O B → )

Векторы и являются радиус-векторами точек А и В , а значит:

O A → = ( x A , y A , z A ) и O B → = ( x B , y B , z B ) , следовательно

O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )

Таким образом, точка С , делящая отрезок А В в пространстве в заданном отношении λ , имеет координаты: ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )

Рассмотрим теорию на конкретных примерах.

Исходные данные: точка С делит отрезок А В в отношении пять к трем. Координаты точек А и В заданы A ( 11 , 1 , 0 ) , B ( — 9 , 2 , — 4 ) .

Решение

По условию задачи λ = 5 3 . Применим полученные выше формулы и получим:

x A + λ · x B 1 + λ = 11 + 5 3 · ( — 9 ) 1 + 5 3 = — 3 2

y A + λ · y B 1 + λ = 1 + 5 3 · 2 1 + 5 3 = 13 8

z A + λ · z B 1 + λ = 0 + 5 3 · ( — 4 ) 1 + 5 3 = — 5 2

Ответ: C ( — 3 2 , 13 8 , — 5 2 )

Исходные данные: необходимо определить координаты центра тяжести треугольника А В С .

Заданы координаты его вершин: A ( 2 , 3 , 1 ) , B ( 4 , 1 , — 2 ) , C ( — 5 , — 4 , 8 )

Решение

Известно, что центром тяжести любого треугольника является точка пересечения его медиан (пусть это будет точка М ). Каждая из медиан делится точкой М в отношении 2 к 1 , считая от вершины. Исходя из этого, найдем ответ на поставленный вопрос.

Допустим, что А D – медиана треугольника А В С . Точка М – точка пересечения медиан, имеет координаты M ( x M , y M , z M ) и является центром тяжести треугольника. М , как точка пересечения медиан, делит отрезок А D в отношении 2 к 1 , т.е. λ = 2 .

Найдем координаты точки D . Так как A D – медиана, то точка D – середина отрезка В С . Тогда, используя формулу нахождения координат середины отрезка, получим:

x D = x B + x C 2 = 4 + ( — 5 ) 2 = — 1 2 y D = y B + y C 2 = 1 + ( — 4 ) 2 = — 3 2 z D = z B + z C 2 = — 2 + 8 2 = 3

Вычислим координаты точки М :

x M = x A + λ · x D 1 + λ = 2 + 2 · ( — 1 2 ) 1 + 2 = 1 3

y M = y A + λ · y D 1 + λ = 3 + 2 · ( — 3 2 ) 1 + 2 = 0

z M = z A + λ · z D 1 + λ = 1 + 2 · 3 1 + 2 = 7 3

Урок 3

расстояние между двумя точками.

деление отрезка в данном отношении.

Расстояние между двумя точками.

теорема 4 . для любых двух точек м 1 (х 1 ;у 1 ) и м 2 (х 2 ;у 2 ) Плоскости расстояние d между ними выражается формулой:

доказательство. оПустим из точек м 1 и м 2 ПерПендикуляры м 1 в и м 1 а соответственно на оси оу и ох и обозначим через точку к точку Пересечения Прямых м 1 в и м 1 а. точка к имеет координаты (х 2 ;у 1 ). согласно теореме 3 имеем l м 1 к l = l х 2 — х 1 l и l м 2 к l = l у 2 — у 1 l.

так как Полученный треугольник Прямоугольный, то По теореме Пифагора

d 2 = м 1 м 2 2 =м 1 к 2 +м 2 к 2 или . теорема доказана.

Пример 1. найти расстояние между точками а(-2;3) и в(5;4).

решение. исПользуя данную формулу, Получим:&amP;NbSP;

уПражнение. даны точки а(0;0), в(3;-4), с(-3;4). найдите расстояние между точками: а) аи в; б) в и с; в) а и с. (ответ: а) 5, б) 10, в) 5)

теорема 5. для любых трех точек a ( x 1 ; y 1 ), b ( x 2 ; y 2 ) и c ( x 3 ; y 3 ), не лежащих на одной Прямой, Площадь S треугольника авс находится По формуле: S abc =1/2 |( x 2 – x 1 )( y 3 – y 1 ) – ( x 3 – x 1 )( y 2 – y 1 )| .

доказательство. Площадь треугольника авс, изображенного на рисунке, можно найти так:

S=S adec +S bceF — S abFd (*) , где S adec , S bceF , S abFd — Площади соответствующих траПеций.

выражая Площадь каждой траПеции через координаты точек а, в и с, находим:

S adec =1/2 (ad+ce)*de = 1/2( x 3 – x 1 )( y 3 + y 1 )

S bceF =1/2 (ec+bF)*eF = 1/2 ( x 2 – x 3 )( y 2 + y 3 )

S abFd =1/2 (ad+bF)*dF = 1/2 ( x 2 – x 1 )( y 2 + y 1 )

Подставим эти равенства в формулу (*), Получим формулу: S =1/2 |( x 1 – x 2 )( y 1 + y 2 ) +( x 2 – x 3 )( y 2 + y 3 ) + ( x 3 – x 1 )( y 3 + y 1 )| , из которой После Преобразований следует искомая формула для Площади треугольника.

формула Площади треугольника верна для любого расПоложения точек а, в, с на Плоскости, а не только для такого, как Показано на рисунке, При условии, что обход вершин а > в > с совершается Против часовой стрелки.

если же вершины треугольника авс расПоложены так, что обход а>в>с совершается По часовой стрелке, то Правая часть формулы меняет знак на ПротивоПоложный и для Площади треугольника авс надо взять то же выражение со знаком «-«.

Пример 2. даны точки а(1;1), в(6;4), с(8;2). найти Площадь треугольника авс.

решение. Подставляя координаты точек в формулу для Площади треугольника, Получим:

S abc =1/2 |(6 – 1)(2 –1) – (8 – 1)(4 – 1)| = 1/2 l-16l =8

уПражнение. вычислить Площадь треугольника, вершинами которого являются точки: а) а(2;-3), в(3;2), с(-2;5) б) м(-3;2), к(5;-2), о(1;3) в) х(3;-4), у(-2;3), т(4;5). (ответ: а) 14, б) 12, в) 25).

Деление отрезка в данном отношении.

Пусть на Плоскости дан Произвольный отрезок м 1 м 2 и Пусть м — любая точка этого отрезка, отличная от точки м 2 .

число л , оПределяемое равенством называется отношением , в котором точка м делит отрезок м 1 м 2.

задача о делении отрезка в данном отношении состоит в том, чтобы По данному отношению Л и данным координатам точек м 1, м 2 найти координаты точки м.

эту задачу Позволяет решить следующая теорема.

терема 6. если точка м(х;у) делит отрезок м 1 м 2 в отношении Л ;то координаты этой точки оПределяются формулами: ; ,где (х 1 ; у 1 ) — координаты точки м 1 , (х 2 ; у 2 ) — координаты точки м 2 .

доказательство. Пусть Прямая м 1 м 2 не ПерПендикулярна оси ох. оПустим ПерПендикуляры из точек м 1, м 2 , м на ось ох и обозначим точки их Пересечения с осью ох соответственно через р 1 , р и р 2 (см рис). на основании известной теоремы о ПроПорциональности отрезков Прямых, заключенных между Параллельными Прямыми, заключаем, что = . но По теореме 3 имеем l р 1 р l=lх-х 1 l и l рр 2 l=lх 2 -хl. так как числа

( x – x 1 ) и (х 2 – х) имеют один и тот же знак ( При x 1 x 2 они Положительны, а При x 1 > x 2 – отрицательны), то . Поэтому , откуда . если Прямая м 1 м 2 ПерПендикулярна оси ох, то х 1 = х 2 =х и эта формула также, очевидно, верна. формула для вычисления второй координаты у выводится аналогично. теорема доказана.

следствие. если точка м(х;у) середина отрезка м 1 м 2 ,то Л =1, то координаты этой точки Примут вид: и

,где (х 1 ; у 1 ) — координаты точки м 1 , (х 2 ; у 2 ) — координаты точки м 2 . таким образом, каждая координата середины отрезка равна Полусумме соответствующих координат.

Пример 3. даны точки а(-2;3) и в(4;6). отрезок, ограниченный этими точками, разделен в отношении Л =2. найдите координаты точки м(х;у).

решение. Подставим координаты точек и Л =2 в формулы, Получим: х= (-2+2*4) / (1+2)=2; у= (3+2*6) / (1+2)=5. следовательно, координаты точки деления м(2;5).

таким образом, из рассмотренных нами задач наглядно видно, как метод координат Позволяет решить геометрические задачи чисто алгебраически.

на оси ох найдите точку, расстояние которой от точки а(3;4) равно 5. (ответ: (6;0) и (0;0))

точка м является серединой отрезка оа, соединяющего начало координат о с точкой а(-5;2). найдите координаты точки м. (ответ: (-2,5;1))

точка м(2;3) делит отрезок ав в отношении 1:2. найдите координаты точки в, если известно, что точка а имеет координаты (1;2). (ответ: в(4;5))

вершинами треугольника служат точки а(-2;1), в(2;2), с(4;у). Площадь треугольника равна 15. оПределите ординату вершины с. (ответ: 10 или -5).

найдите координаты центра тяжести однородной Пластинки, имеющей форму треугольника с вершинами а(-2;1), в(2;-1), с(4;3).(ответ: х=4 / 3, у=1, указание: центр тяжести треугольника находится в точке Пересечения его медиан, которая делит каждую из медиан в отношении 2:1, считая от вершины)

Площадь треугольника равна 3, две его вершины — точки а(3;1) и в(1;-3). найдите координаты третьей вершины, если известно, что она лежит на оси ординат. (ответ: с(0;-8) или с(0;2))

Площадь Параллелограмма равна 12, две его вершины — точки а(-1;3) и в(-2;4). найдите две другие вершины Параллелограмма, если известно, что точка Пересечения его диагоналей лежит на оси абсцисс. (ответ: (-7;-3) и (-6;-4) или (17;-3) и (18;-4))

вершины треугольника — точки а(3;6), в(-1;3) и с(2;-1). найдите длину его высоты, Проведенной из вершины с. (ответ:5)

три вершины Параллелограмма- точки а(3;7), в(2;-3) и с(-1;4). найдите длину высоты, оПущенной из вершины в на сторону ас. (ответ: 7 или 4)

отрезок, ограниченный точками а(1;-3) и в(4;3), разделен на три равные части. оПределите координаты точек деления. (ответ: (2;-1) и (3;1))

оПределите координаты концов отрезка а и в, который точками к(2;2) и м(1;5) разделен на три равные части. (ответ: а(3;-1) и в(0;8))

три вершины Параллелограмма — точки а(3;-5), в(5;-3) и с(-1;3). оПределите четвертую вершину, ПротивоПоложную в. (ответ: (-3;1))

найдите Площадь Пятиугольника с вершинами о(0;0), а(3;-2), в(5;-1), с(8;4) и е(4;5). (ответ: 29,5)

Автор: Вяликова Мария Владимировна — учитель математики и информатики высшей квалификационной категории МАОУ Пролетарская СОШ Новгородского района Новгородской области