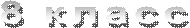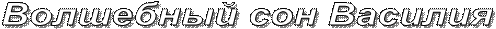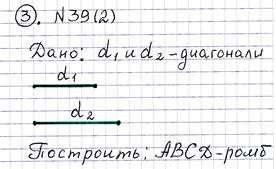Творческие задания по теме четырехугольники

Данная работа определяет следующие задачи:

— совершенствование, развитие, углубление знаний, умений, навыков по данной теме;

— развитие мыслительной деятельности: умение анализировать, обобщать, классифицировать;

— освоение компетенций: учебно – познавательной, коммуникативной, рефлексивной, личностного саморазвития.

Тема « Четырехугольники», в частности задачи на вычисления площадей четырехугольников стали традиционными для ЕГЭ и ГИА.

Творческая работа имеет следующую структуру.

Введение дает обобщенное представление о геометрии как актуальной востребованной науке, показывает связь между математикой в целом и окружающим миром.

Классификация основных понятий представляет систематизированный материал по каждому представителю четырехугольников и их характеристики.

Свойства четырехугольников на примере прямоугольника, квадрата, ромба – это обобщение и сравнение свойств данных фигур.

Применение темы « Площади четырехугольников» к решению задач в ГИА и ЕГЭ. Это основные понятия темы, примеры типовых задач, актуальность данного материала.

Видео:Миникурс по геометрии. ЧетырехугольникиСкачать

Скачать:

Бесплатный марафон подготовки к ЕГЭ на зимних каникулах

Учи.Дома запускает бесплатный марафон в котором каждый день. В течении 5 дней утром ты будешь получать одно задание по выбранному предмету, а вечером его решение. Твоя задача, успеть выполнение задание до того как получишь ответ.

Бесплатно, онлайн, подготовка к ЕГЭ

Видео:ГЕОМЕТРИЯ 8 класс: Четырехугольники | Видеоурок с теорией и решением задачиСкачать

Предварительный просмотр:

Кром Ирины Владимировны

Роль геометрии в современном мире.

Глава 1. Геометрия четырехугольников. Классификация основных понятий.

2.1. Вписанный и описанный четырехугольник.

2.2. Параллелограмм и прямоугольник.

2.3. Квадрат и ромб.

Глава 2.Свойства четырехугольников на примере прямоугольника, квадрата, ромба.

Глава 3. Метод площадей. Задачи.

Приложение по теме « Четырехугольники». Тест.

Введение. Роль геометрии в современном мире.

Вопрос о том, какую роль играет математика и её изучение в формировании личности, столь же древен , как и первые теоретические попытки его осмысления.

Выдающийся швейцарский математик И.Г. Песталоцци ( 1746 – 1827) утверждал, что знание математики позволяет более правильно воспринимать окружающий мир, находить истину, избегать искажений и предрассудков, укреплять здравый смысл. Он писал, что математика является « фундаментом, на котором строится способность правильно воспринимать действительность , и создаёт основу для развития ума и сообразительности в отношении практических вопросов». [ 16, с. 280 ]

В настоящее время повсеместное применение компьютеров, строительство модели мира раздвинули границы прикладного аспекта математической науки до грандиозных масштабов. Схематизация конкретных объектов, построение математических моделей, анализ, дедукция, выделение и поддержание уровней абстракции, прогнозирование, конструирование алгоритмов и их критериальная оценка – всё это далеко не полный перечень необходимого современного интеллекта.

Математика – метод и язык познания окружающего мира, это наука, прерогатива и обязанность которой – развитие абстрактного и логического мышления, т.е. качеств личности, которые необходимы для освоения новых областей знаний и облегчения адаптации к постоянно меняющимся условиям жизни.

Так , размышляя о предназначении математики, следует отменить, что в глубине души у каждого человека живет тайная надежда понять свой внутренний мир, совершенствовать себя и тем самым, возможно повлиять на действительность , а математика дает такую возможность.

Любая наука возникла из практических потребностей людей. Следуя этим потребностям, математика претерпела разделение на две самостоятельные ветви, которые тесно взаимосвязаны друг с другом. Это алгебра и геометрия. Остановимся на геометрии.

В повседневной жизни человеку приходилось размышлять о форме окружающих предметов, производить вычисления, связанные с землемерием, строительным делом, с нахождением объёмов различных тел. Такими задачами в разные времена приходилось заниматься всем народам, населяющим землю, что и способствовало возникновению и накоплению геометрических знаний.

Так, имеются сведения о значительном развитие этих знаний в Египте

более чем за 2 тысячи лет до нашей эры.

Известно, что при разливе реки Нил вода смывала границы земельных участков, принадлежащих отдельным лицам. После спада воды эти границы приходилось восстанавливать, и человеку нужны были знания по измерению земли.

Историк того времени рассказывает: « Если Нил заливал чей – либо участок, то пострадавший обращался к царю и докладывал ему о случившимся. Тогда царь посылал землемеров ( геометров): они замеряли, на сколько уменьшился участок, и сообразно этому понижали налог».

Благодаря мореплаванию и торговле с Египтом греки не только усваивали знания египтян, но и продолжали их накапливать и обобщать. Не случайно поэтому и происхождение слова « геометрия». « Геометрия» — слово греческое, в переводе на русский язык означает « землемерие».

Греки сумели привести разрозненные геометрические сведения в систему и придать геометрии вид науки. Попытку создать такую науку уже в V веке до н. э. предпринимает греческий ученый Гиппократ, а позднее Леон, но к этому времени накопленных геометрических сведений было еще мало. Поэтому их труды хотя и были шагом вперед в создании геометрической науки, но не получили широкого распространения.

Геометрия как наука о свойствах геометрических фигур наиболее удачно была изложена греческим ученым Евклидом в III в. до н. э. В своих тринадцати книгах под общим названием « Начала» Евклид не только

систематизировал тот геометрический материал, который был известен до него, но и дополнил его собственными изысканиями и открытиями.

Главная заслуга Евклида состояла в том, что он показал способ изложения геометрического материала, которым пользуются и теперь.

Практическая деятельность людей ставила все новые и новые задачи, решение которых способствовало дальнейшему развитию и совершенствованию геометрических знаний, относящихся не только к измерению земли, но и к другим видам человеческой деятельности. И теперь геометрия обогащается новыми знаниями, необходимыми людям.

Геометрия является очень мощным средством развития личности в самом широком диапазоне. Геометрия, на фоне дисциплин математического цикла, выделяется свободолюбивым характером, нежеланием подчиняться стандартам, нормам, алгоритмам.

Знания – основная цель изучения геометрии. Но нужно всегда помнить, что геометрия есть феномен общечеловеческой культуры. Человек не может развиваться культурно и духовно, если он не изучал геометрию. Таким образом, возникновение геометрии обусловлено не только практическими потребностями человека, но и духовными.

Своеобразие геометрии заключается в неразрывной связи живого воображения со строгой логикой. Можно сказать, что геометрия в своей сути и есть пространственное воображение, пронизанное и организованное строгой логикой. Научной и нравственной основой геометрии является принцип доказательности всех утверждений. Во всяком подлинно геометрическом предложении, будь то аксиома, определение, теорема или задача, непременно присутствуют два элемента : наглядная картинка и строгая формулировка, строгий логический вывод.

Наглядность, воображение принадлежат больше искусству, а строгая логика – привилегия науки. Сухость точного вывода и живость наглядной картинки – геометрия соединяет в себе эти две противоположности. При ее изучении в одно целое соединяются наглядные картинки и строгие формулировки и доказательства.

Геометрия способствует формированию навыков логического мышления, развитию пространственных представлений. На первое место выдвинуто формирование логического мышления – это далеко не случайно. Возникнув из практических нужд, уже со времён Евклида геометрия изучается не для того, чтобы «измерять землю» , а ради совершенствования мышления.(Царь Птолемей, который возжелал изучать геометрию и получил от Евклида легендарную отповедь: « В геометрии нет царского пути!» — конечно же, не собирался стать землемером.) Совершенно четко высказался на этот вопрос А.В.Погорелов: «… Главная задача преподавания геометрии в школе – научить учащегося логически рассуждать, аргументировать свои утверждения, доказывать…» и, далее, «…Вряд ли найдется хотя бы один , кому не придется рассуждать, анализировать, доказывать»…

Геометрия возникла из практических задач , ее предложения выражают реальные факты и находят многочисленные применения. В конечном счете в основе всей техники так или иначе лежит геометрия, потому что она проявляется везде, где нужна малейшая точность в определении формы и размеров. И технику, и инженеру, и рабочему , и архитектору, и модельеру необходимо геометрическое воображение.

Установлено , что каждое десятое изобретение сделано с применением геометрии , за счет выбора подходящей формы, удачного размещения и т.п. А ведь изобретений миллионы.

Математика, геометрия в частности, представляет собой могущественный инструмент познания природы и создания техники.

Школьное образование в современных условиях призвано обеспечить функциональную грамотность и социальную адаптацию обучающихся на основе приобретения ими компетентного опыта в сфере учения, познания, личностного развития, ценностных ориентаций. Это определяет направленность целей обучения на формирование компетентной личности, способной к жизнедеятельности и самоопределения в информационном обществе, ясно представляющей свои потенциальные возможности, ресурсы и способы реализации выбранного жизненного пути.

Изучение математики направлено на реализацию целей и задач, сформированных в Государственном стандарте общего образования по математике. Целями данной работы являются систематизация сведений о четырехугольниках и их свойствах, рассмотрение решений задач, в которых раскрываются свойства данных четырехугольников, обобщение понятия площади фигур, формирование практических навыков вычисления площадей четырехугольников в ходе решения задач, так как вычисление площадей фигур является составной частью решения задач на многогранники в курсе стереометрии.

Данная работа определяет следующие задачи:

— совершенствование, развитие, углубление знаний, умений, навыков по данной теме;

— развитие мыслительной деятельности: умение анализировать, обобщать, классифицировать;

— освоение компетенций: учебно – познавательной, коммуникативной, рефлексивной, личностного саморазвития.

Тема « Четырехугольники», в частности задачи на вычисления площадей четырехугольников стали традиционными для ЕГЭ и ГИА.

Творческая работа имеет следующую структуру.

Введение дает обобщенное представление о геометрии как актуальной востребованной науке, показывает связь между математикой в целом и окружающим миром.

Классификация основных понятий представляет систематизированный материал по каждому представителю четырехугольников и их характеристики.

Свойства четырехугольников на примере прямоугольника, квадрата, ромба – это обобщение и сравнение свойств данных фигур.

Применение темы « Площади четырехугольников» к решению задач в ГИА и ЕГЭ. Это основные понятия темы, примеры типовых задач, актуальность данного материала.

Глава 1. Геометрия четырехугольников. Классификация основных понятий.

Представление о некоторых геометрических фигурах складывается с первых уроков математики. Знакомство с такими фигурами ,как треугольник, прямоугольник, окружность, круг и др., умение измерять отрезки с помощью линейки с миллиметровыми делениями, измерять углы с помощью транспортира – это лишь самые первые геометрические сведения.

При изучении геометрии состоится знакомство с новыми фигурами и со многими важными свойствами уже известных фигур. В планиметрии рассматриваются свойства фигур на плоскости. Примерами таких фигур являются отрезки, треугольники, многоугольники.

Подробно познакомимся с одним из видов фигур – четырехугольник.

2.1. Четырехугольником называется фигура, состоящая из четырех точек (вершин), никакие три из которых не лежат на одной прямой, и четырех последовательно соединяющих их непересекающихся отрезков (стороны).

Вершины четырехугольника называются соседними , если они являются концами одной из его сторон. Вершины , не являющиеся соседними , называются противоположными. Отрезки, соединяющие противолежащие вершины четырехугольника, называются диагоналями.

Четырехугольник ( как и любой многоугольник) называется выпуклым, если он расположен в одной полуплоскости относительно прямой, содержащей любую его сторону.

Познакомимся с одним из свойств четырехугольника.
Теорема. Сумма углов четырехугольника равна 360 о .
Действительно, поделив четырехугольник диагональю на два треугольника, получаем, что сумма его углов равна сумме углов этих двух треугольников. Зная, что сумма углов треугольника равна 180 о , получаем искомое: 2 180 о =360 о

Встречаются вписанные и описанные четырехугольники, имеющие определённые признаки и свойства.

Вписанный четырехугольник – четырехугольник, все вершины которого принадлежат данной окружности. Окружность называют описанной. Точка пересечения серединных перпендикуляров, проведенных ко всем его сторонам – это центр окружности, описанной около четырехугольника.

Теорема. У любого четырехугольника, вписанного в окружность, суммы пар противоположных углов равны 180 о .
Углы А и С оба опираются на дугу BD только с разных сторон, то есть охватывают всю окружность, а сама окружность – это дуга величиной в 360 о , но мы знаем теорему, которая гласит, что величина вписанного угла равна половине угловой величины дуги, на которую он опирается, поэтому можем утверждать, что сумма этих углов (А и С в частности) равна 180 о . Тем же способом можно доказать эту теорему и для другой пары углов.

Существует обратная теорема данной.

Теорема . Около четырехугольника можно описать окружность тогда и только тогда, когда сумма противоположных углов равна 180 градусам.

Четырехугольник, каждая сторона которого касается данной окружности, называется описанным . Основной его признак звучит так: если в четырехугольнике сумма двух его противоположных сторон равна сумме двух других его сторон, то в четырёхугольник можно вписать окружность.

Теорема .Если в четырехугольник можно вписать окружность, то суммы длин его противоположных сторон равны.
Для доказательства этой теоремы воспользуемся теоремой ,которая гласит: Отрезки касательных, проведенных из одной точки к окружности, равны, т.е. ВК=ВР, СР=СН, DH=DT и АТ=АК. Суммируем стороны АВ и CD: AB+CD=(AK+KB)+(DH+HC)=AT+BP+DT+CP=(AT+TD)+(BP+PC)=AD+BC, ч.т.д.

Рассмотрим пример обратной теоремы.

Теорема . В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны.

Доказательство: Пусть ABCD — данный четырехугольник, у него AB + CD = AD + BC. Проведем биссектрисы его углов A и D. Эти биссектрисы не параллельны, а значит, пересекаются в некоторой точке O. Опустим из точки O на стороны AB, AD и CD перпендикуляры OK, OL и OM. Тогда OK=OL, и OL=OM, а значит, окружность с центром в точке O и радиусом OK касается сторон AB, AD и CD данного четырёхугольника. Проведём из точки B касательную к этой окружности. Пусть эта касательная пересекает прямую CD в точке P.

Тогда ABPD — описанный четырёхугольник. Следовательно, по свойству описанного четырёхугольника, AB + DP = AD + BP. Также, по условию, AB+ CD = AD + BC. Следовательно, BP + PC = BC, а значит, по неравенству треугольника, точка P лежит на отрезке BC. Следовательно, прямые BP и BC совпадают, а значит, прямая BC касается окружности с центром в точке O, то есть ABCD — описанный четырёхугольник по определению. Теорема доказана.

В окружающей нас жизни мы часто встречаемся с предметами, имеющими форму четырехугольника: оконная рама, нагрудный значок, панели для постройки домов и другие предметы. В большом мире геометрических фигур существуют яркие представители четырехугольника : параллелограмм и прямоугольник, ромб и квадрат, трапеция. Рассмотрим каждый четырёхугольник, познакомимся с их свойствами .

2.2.Параллелограм и прямоугольник.

Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны. Существуют несколько признаков параллелограмма. Перечислим их.

Четырехугольник является параллелограммом,

если противоположные стороны четырехугольника попарно равны; если противоположные углы попарно равны; если соседние углы четырехугольника, т.е. углы прилежащие к одной стороне,

составляют 180 градусов; если диагонали четырехугольника взаимно делятся в точке пересечения пополам; если четырехугольник имеет пару равных параллельных между собой сторон.

В геометрии рассматривают частные случаи параллелограмма: прямоугольник, ромб, квадрат.

Прямоугольник — это параллелограмм, в котором все углы прямые. Так как прямоугольник является параллелограммом, то он обладает всеми свойствами параллелограмма: в прямоугольнике противоположные стороны равны , а диагонали точкой пересечения делятся пополам. Но есть и частные свойства. Рассмотрим их.

Теорема. Диагонали прямоугольника равны.

Для доказательства достаточно рассмотреть два прямоугольных треугольника ABD и ABC. Они равны по двум катетам( противолежащие стороны равны) , поэтому равны их гипотенузы – диагонали AC и BD.

Прямоугольник также имеет признаки параллелограмма, но существуют частные признаки.

Теорема. Если в четырехугольнике диагонали равны и точкой пересечения делятся пополам, то такой четырехугольник является прямоугольником.

Из равенства диагоналей следует и равенство частей, на которые они разбиваются при пересечении, т.е. точка пересечения диагоналей равноудалена от вершин четырехугольника, а следовательно около него можно описать окружность. Зная теорему: вписанные углы опирающиеся на диаметр, равны 90 градусов, заключаем, что все углы данного четырехугольника прямые. Из этого доказательства также вытекает следующие утверждения:

-диаметр описанной около прямоугольника окружности равен его диагонали;

-вокруг любого прямоугольника можно описать

окружность.

-квадрат диагоналей прямоугольника равен

сумме квадратов двух соседних сторон.

-периметр прямоугольника равен удвоенной сумме соседних сторон

-при пересечение биссектрис внутренних углов произвольного параллелограмма образуется прямоугольник.

2.3. Ромб и квадрат.

Ромб и квадрат – это параллелограммы. Поэтому они обладают всеми свойствами параллелограмма. Но существуют свойства, принадлежащие только этим фигурам. Рассмотрим их.

Особые свойства ромба.

Теорема. Высоты ромба равны. BK = BF.

Теорема . В любой ромб можно вписать окружность.

r = = =

Квадратом называется прямоугольник, у которого все стороны равны. Прямоугольник является параллелограммом, поэтому и квадрат является параллелограммом, у которого все стороны равны, т.е. ромбом. Отсюда следует, что квадрат обладает всеми свойствами прямоугольника и ромба. Сформулируем основные свойства квадрата.
1.Все углы квадрата равны. 2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам. 3.Диагонали квадрата пересекаются под прямым углом, являются биссектрисами его углов. 4. Диагональ квадрата в корень из двух раз больше его стороны.

d = a .

Вокруг любого квадрата можно описать

В любой квадрат можно вписать окружность r = .

N

K M

Трапеция — четырехугольник, две стороны которого параллельны, а другие две не параллельны. Основаниями трапеции называют её параллельные стороны. Боковыми сторонами трапеции называют её непараллельные стороны. Параллельные стороны не могут быть равными, т.к. в противном случае мы имели бы параллелограмм . Поэтому одну из них мы назовем большим , вторую — малым основанием трапеции. Высотой трапеции можно назвать любой отрезок перпендикуляра, проведенного из вершины на соответственно противоположную сторону (для каждой вершины есть две противоположные стороны), заключенный между взятой вершиной и противоположной стороной. Но можно выделить «особый вид» высот.
Высотой основания трапеции называют отрезок прямой, перпендикулярной основаниям, заключенный между основаниями.

Средняя линия – отрезок, который соединяет середины боковых сторон.

Рассмотрим еще один пример – свойство отрезка , параллельного основаниям трапеции. В трапеции ABCD основания AD и BC равны соответственно a и b. Через точку Е, принадлежащую стороне AB и делящую ее в отношении m : n, проведена прямая, параллельная основаниям трапеции и пересекающая сторону CD в точке F. Доказать, что EF = .

Решение. Проведем через точку С прямую параллельную АВ. Пусть она пересекает EF в точке Р, а AD в точке О. Треугольники CPF и CQD подобны.

Q Следовательно, = .

Учитывая, что , CP : CQ = n : ( m +

+ n), PF = EF – b, QD =a – b,

получим = . Отсюда следует, что EF = .

Глава 2. Свойства четырёхугольников на примере прямоугольника, ромба, квадрата.

Изучив классификацию четырехугольников и их основные свойства , можно рассмотреть дополнительный материал к школьной программе. Материал содержит следующие темы:

1. Вписанные и описанные четырехугольники.
2. Свойство четырехугольников на примере прямоугольника, квадрата и ромба.
3. Трапеция.

Настоящее занятие посвящено задачам на нахождение элементов четырехугольников и радиусов вписанной и описанной окружности. Задачи направлены на развитие геометрических представлений , выработку умений и навыков нахождения элементов четырехугольников.

Вспомним теоретический материал.

Вписанный четырехугольник – четырехугольник, все вершины которого принадлежат данной окружности. Окружность называют описанной. Точка пересечения серединных перпендикуляров, проведенных ко всем его сторонам – это центр окружности, описанной около четырехугольника.

Важным признаком вписанного четырехугольника является равенство суммы противоположных углов четырёхугольника 180 0 .

Четырехугольник, каждая сторона которого касается данной окружности, называется описанным . Основной его признак звучит так: если в четырехугольнике сумма двух его противоположных сторон равна сумме двух других его сторон, то в четырёхугольник можно вписать окружность.

Суммы противоположных углов четырехугольника, вписанного в окружность, равны 180 о .

Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен 6.

Найдите радиус окружности, описанной около квадрата со стороной, равной .

Меньшая сторона прямоугольника равна 5. Угол между диагоналями равен 60 о . Найдите радиус описанной окружности

Задача. Докажите, что если в выпуклом четырехугольнике суммы противоположных сторон равны, то в этот четырехугольник можно вписать окружность.

Решение. Пусть в выпуклом четырехугольнике ABCD AB + CD = BC + AD. (1)

Точка О пересечение угла биссектрисы углов А и В равно удалены от сторон

AD, AB и BC, поэтому можно провести окружность с центром О, касающуюся указанных трех сторон. Докажем , что эта окружность касается также стороны CD и , значит , является вписанной в четырехугольник ABCD. Предположим, что это не так. Тогда прямая CD либо не имеет общих точек с окружностью, либо является секущей. Рассмотрим первый случай. Проведем касательную C 1 D 1 ,параллельную стороне CD ( C 1 и D 1 — точки пересечения касательной со сторонами BC и AD). Так как ABC 1 D 1 – описанный четырехугольник, то по свойству его сторон AB + C 1 D 1 = BC 1 + AD 1 . (2)

Но BC 1 = BC – C 1 C, AD 1 = AD –D 1 D, поэтому из равенства (2) получаем:

C 1 D 1 + C 1 C + D 1 D = BC + AD – AB.

Правая часть этого равенства в силу (1) равна CD. Таким образом, приходим к равенству C 1 D 1 + C 1 C + D 1 D = CD,т.е. в четырехугольнике C 1 CDD 1 одна сторона равна сумме трех других сторон. Но этого не может быть, и , значит, наше предположение ошибочно. Аналогично можно доказать, что прямая CD

не может быть секущей окружности. Следовательно , окружность касается стороны CD, что и требовалось доказать.

Рассмотрим задачу. Пусть в четырёхугольнике ABCD . (1) Проведем окружность через три вершины фигуры: A,B,D – и докажем, что она проходит через вершину С , т.е. является описанной около четырехугольника ABCD. Предположим , что это не так. Тогда вершина С лежит либо внутри круга , либо вне его. Рассмотрим первый случай. В этом случае ( DAB + EF) ,и, следовательно, DAB. Так как DEF, то ( BED + DAB) = 360 .

Итак, мы получили , что . Но это противоречит условию (1), и, значит , наше предположение не верно. Следовательно , вершина С лежит на окружности, что и требовалось доказать.

Глава 4. Свойства прямоугольника, квадрата, ромба.

Цель данного занятия – обобщение и систематизация знаний о прямоугольниках, ромбах и квадратах, их свойствах и признаках. Задачи направлены на выработку умений и на развитие геометрических представлений о фигурах данной темы, а также на развитие навыков нахождения элементов четырехугольников. Решением одной из важных задач общеобразовательной и профессиональной школы является усиление прикладной направленности обучения. В этой связи важно выработать у учащихся умение при решении конкретных вопросов ориентироваться на существенные свойства объектов и явлений. Большие возможности для формирования такого умения имеются при изучении темы «Четырёхугольники».
Предлагаемый материал представляет большие возможности для организации разных форм коллективной учебно-познавательной деятельности учащихся, закладывает фундамент для развитая умения применять геометрические знания при решении вопросов жизненно–практического и производственного характера.
В качестве ведущей идеи берем идею четкого разграничения свойств и признаков параллелограмма и его частных видов.

Прежде всего нужно добиться, чтобы учащиеся научились различать понятия «свойство фигуры» и «признак фигуры». Если дано, что фигура параллелограмм, и исходя из этой посылки доказывают некоторые соотношения между элементами рассматриваемой фигуры, то каждое из этих соотношений называется свойством фигуры, о которой речь идет в условии теоремы.

Например, теорема: «У параллелограмма противоположные стороны равны, противоположные углы равны», кратко может быть записано так:

Дано: АВСД – параллелограмм.

Доказать: 1) АВ = СД; АД = ВС

2)  А =  С;  В =  Д

Каждое из соотношений (1), (2) заключения теоремы дает свойство параллелограмма.

В теореме же «Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм» указаны соотношения между элементами некоторого четырехугольника (АО=ОС, ВО=ОД) и доказывается, что при их выполнении четырехугольник будет принадлежать к классу параллелограммов (будет являться параллелограммом). В этом случае условия (АО=ОС, ВО=ОД) называют признаками параллелограмма, т. к. при их выполнении мы можем смело утверждать, что четырехугольник, для которого выполняются эти условия, обязательно будет параллелограммом (теорема).

Более глубокого и осознанного усвоения понятий «свойство» и «признак» можно добиться, если связать их с понятиями «необходимое условие», «достаточное условие», «необходимое и достаточное условие».

Сообщаем школьникам, что любая теорема может быть записана в виде А В, где А — условие теоремы (что дано), а В — заключение теоремы (что требуется доказать).

Если доказана теорема А В, то А является достаточным для В (как только есть А, то сейчас же будет и В), а В — необходимо для А, из А неизменно (необходимо) следует В.

Ещё более убедительное обоснование того, почему условие В считается необходимым для А, можно дать, если познакомить учащихся с вопросом о видах теорем и связи между ними. Записываем схему:

(3) нет А нет В нет В нет А (4)

Сообщаем, что если утверждение (1) назвать прямым, то утверждение (2) будет к нему обратным, утверждение (3) — противоположным прямому, а (4)—противоположно обратному. Далее доказывается, что из справедливости утверждения (1) следует справедливость утверждения (4) [(1) (4)] и наоборот, т. е. (4) (1).

Сообщается, что если (1) (4), то утверждения называются эквивалентными. Аналогично эквивалентны утверждения (2) и (3) [(2) (3)].

Словами формулу (1) (4) можно расшифровать так: если из условия А следует (вытекает) условие В, то без В нет и А, иными словами В необходимо для А (без В не будет и А).

А далее сообщаем, что необходимое условие дает нам свойство, а если условие не только необходимо, но и достаточно, то получаем признак.

Иными словами, чтобы получить свойство В какого-нибудь объекта А, достаточно доказать теорему А В, а чтобы убедиться, что рассматриваемое свойство В является признаком, следует ещё доказать теорему В А (обратную).

Вместе с учащимися вспоминаем все свойства параллелограмма и составляем таблицу.

Дано: АВСД – параллелограмм

Доказать: 1) АВ || СД

1. ВС || АД
2. АВ = СД
3. ВС = АД
4. АО = ОС
5. ВО = ОД
6.  А =  С
7.  В =  Д
8.  А +  В = 180 0
9.  С +  В = 180 0
10.  С +  Д = 180 0
11.  А +  Д = 180 0

Обращаем внимание на тот факт, что каждое из условий 1–12 вытекает из того, что АВСД — параллелограмм, следовательно, каждое из них является необходимым условием того, чтобы четырехугольник АВСД был параллелограммом. Легко убедиться, что из каждого из условий 1–12 не следует, что АВСД — параллелограмм (например, если дано, что АВ II СД, что имеем трапецию, ибо ВС || АД) .

Таким образом, каждое из условий 1–12, взятое в отдельности, признаком параллелограмма не является. Теперь начнём комбинировать свойства по два (Сколько таких комбинаций будет? Как сосчитать все комбинации, чтобы быть убеждённым, что ни одна не пропущена?). Убеждаемся, что некоторые из комбинаций дают признак параллелограмма. Какие из комбинаций по два дают известные уже вам признаки параллелограмма? [(1, 2), (1, 3), (2, 4), (5, 6)].

В то же время легко видеть, что не каждая из комбинаций по два дает признак параллелограмма. Например, из того что АВ II СД и ВС = АД следует, что фигура АВСД — равнобочная трапеция, а не параллелограмм.

Естественно встает вопрос, сколько же всего признаков у параллелограмма? Для ответа на этот вопрос нужно перебрать все возможные комбинации и либо доказать полученную теорему, либо привести пример, опровергающий её (контрпример). Ясно, что эта работа на уроке проделана быть не может. Она может быть дана в качестве индивидуальных заданий на дом хорошо успевающим учащимся, или еще лучше, предложена в качестве коллективной работы кружковцам. Здесь встают интересные вопросы о планировании работы, о разделении труда при решении этой проблемы, об организации самоконтроля и взаимоконтроля, о подведении окончательных итoгoв, т.e. вопросы, возникающие при организации любой трудовой деятельности.

Далее аналогичную работу можно провести по выяснению признаков прямоугольника и ромба. Но этой работе должно предшествовать уточнение определений прямоугольника и ромба. Действительно, достаточно потребовать, чтобы у параллелограмма был один прямой угол, т. к. из условия (АВСД — параллелограмм; А=90 0 ) следует, что В=90 0 , С=90 0 , Д=90 0 . Для доказательства этого факта достаточно воспользоваться известными свойствами углов параллелограмма.

Аналогично, легко доказать теорему (АВСД — параллелограмм, АВ=ВС АВ=ВС=СД=АД), из которой следует, что ромбом называется параллелограмм, у которого две смежные стороны равны.

Можно не менять привычные учащимся избыточные определения, но обязательно подчеркнуть тот факт, что, чтобы убедиться, что рассматриваемый параллелограмм будет ромбом, достаточно проверить равенство двух смежных сторон, а чтобы убедиться, что он будет прямоугольником, достаточно доказать, что один из его углов прямой.

После этого отмечаем особые свойства диагоналей прямоугольника и ромба и опять ставим вопрос, будут ли эти условия не только необходимыми, но и достаточными, т. е. являются ли эти условия признаками рассматриваемых фигур. Как это проверить? Учащиеся должны сообразить, что для ответа на поставленный вопрос следует сформулировать и доказать теоремы, обратные к теоремам, выражающим свойства диагоналей прямоугольника и ромба.

Запишем одну из этих теорем.

Дано: АВСД — прямоугольник. Доказать: АС=ВД.

Обратное к этой теореме утверждение записывается так:

Дано: в четырёхугольнике АВСД АС=ВД .

Доказать: АВСД — прямоугольник.

Легко убедиться, что это утверждение несправедливо. Приведите примеры, подтверждающие этот факт. Учащиеся могут вспомнить, что диагонали равны у равнобочной трапеции, или начертить произвольный четырехугольник с равными диагоналями. Таким образом, мы убеждаемся, что равенство диагоналей не выделяет прямоугольник из класса четырехугольников (среди четырёхугольников с равными диагоналями есть и не являющиеся прямоугольниками).

Здесь учитель знакомит учащихся с еще одним способом получения утверждений, обратных данному. Замечает, что условие прямой теоремы может быть разбито на две части.

Дано: 1) АВСД — параллелограмм.

Доказать: АС = ВД.

Если теперь поменять местами заключение и вторую часть условия, то мы получим утверждение:

Дано: АВСД — параллелограмм

Доказать: А=90 0 .

Это утверждение легко доказать. Докажите самостоятельно.

Если учащиеся затрудняются, то можно «навести» их на мысль, обратив внимание, что А + Д = 180 0 (АВСД — параллелограмм ). Что осталось теперь доказать? ( А = Д).

Аналогичную работу проводим с установлением признаков ромба, основанных на свойствах его диагоналей. Вспоминаем теорему о

свойствах диагоналей ромба.

Дано: АВСД — ромб.

Доказать: 1) ВД АС;

Для этой теоремы можно составить две обратные:

Теорема 1 Теорема 2

Дано: ВД | АС Дано: ВАС = САД

Доказать: АВСД — ромб. Доказать: АВСД — ромб.

Легко показать, что каждая из этих теорем несправедлива, приведя хотя бы по одному «контрпримеру» ;

Интересен вопрос. А как можно видоизменить первый чертеж чтобы его можно било использовать одновременно для «опровержения» и теоремы 1 и теоремы 2 (Достаточно взять АО=ОС и тогда треугольник AВД равен треугольнику ДВС.

Используя второй способ образования обратных теорем, с которым учащиеся ознакомлены при установлении признака прямоугольника имеем:

Прямая теорема. Дано:

АВСД –параллелограмм, АВ = ВС.

Доказать: ВД АС

Дано: АВСД –параллелограмм, ВД | АС.

Вспоминая уточненное определение ромба, даем такую формулировку обратной теоремы: «Если в параллелограмме диагонали взаимно перпендикулярны, то этот параллелограмм — ромб».

Схема аналитического рассуждения при отыскании доказательства этой теоремы.

АВСД – ромб

АВСД – параллелограмм АВ=ВС

 АВО =  СВО  АОВ =  СОВ

 ВД | АС

АО = ОС ВО – общая  АОВ =  СОВ

АВСД – параллелограмм ВД | АС

Аналогично формулируем второй признак ромба: «Если в параллелограмме диагональ делит угол пополам, то этот параллелограмм — ромб». Аналитическое рассуждение проводится аналогично.

Схематическая запись доказательства

АВСД — параллелограмм АД II ВС ( 1 = 3, 1 = 2)

2 = 3 (АВ=BС, АВСД — параллелограмм) АВСД — ромб.

Обобщая полученные результаты, полезно обратить внимание школьников на тот факт, что равенство диагоналей не выделяет прямоугольник из множества всех четырехугольников, но выделяет его из множества параллелограммов, и предложить им самостоятельно сформулировать аналогичные утверждения (их 2!) для ромба.

Для поверки того, владеют ли учащиеся признаками параллелограмма, ставим перед ними следующую проблему:

Как сформулировать признаки прямоугольника и ромба, основанные на свойствах их диагоналей, чтобы они выделяли прямоугольник и ромб из множества всех четырехугольников? Подсказка, если ученики не справляются: условие АВСД — параллелограмм, каким требованием относительно его диагоналей можно заменить.

1. Если в четырехугольнике диагонали равны и точкой их пересечения делятся пополам, то этот четырехугольник — параллелограмм.

2. Если в четырехугольнике диагонали взаимно перпендикулярны и делятся точкой пересечения пополам, то этот четырехугольник — параллелограмм.

3. Признак формулируем аналогично.

Переходя к выяснению признаков квадрата, подчеркиваем, что квадрат является как частным случаем прямоугольника, так и ромба и следовательно обладает всеми свойствами прямоугольника и всеми свойствами ромба. Ставится проблема: выделить комбинации свойств диагоналей, которые выделяли квадрат из множества прямоугольников, из множества ромбов, из множества параллелограммов, из множества четырехугольников.

Если ученики осмыслили рассмотренный материал о признаках прямоугольника и ромба, то они легко ответят на поставленные вопросы и сформулируют следующие признаки квадрата:

Прямоугольник с взаимно–перпендикулярными диагоналями,

Прямоугольник, у которого диагональ делит угол пополам.

Ромб с равными диагоналями.

Параллелограмм, у которого диагонали равны и взаимно–перпендикулярны.

Параллелограмм, у которого диагонали рваны и делят угол пополам.

Четырехугольник, у которого диагонали равны, взаимно–перпендикулярны и в точке пересечения делятся пополам.

После этого можно перейти к решению задач, требующих применения изученных признаков.

Для приведения в систему материала по теме «Параллелограмм и его виды» очень хороша задача: «Определить вид четырехугольника, который получится, если последовательно соединить отрезками прямых середины сторон произвольного четырехугольника».

После доказательства того факта, что полученный четырехугольник будет параллелограммом, ставится вопрос: «Каким должен быть исходный четырехугольник, чтобы полученный оказался прямоугольником, ромбом, квадратом?».

1. Начертим произвольный четырехугольник.
2. Найдём середины сторон и изобразим схематично на чертеже равенство отрезков.
3. Соединим последовательно полученные точки E, F, M, N.

Вопрос: какой четырехугольник получился?

У разных учащихся ответ будет различным: параллелограмм, прямоугольник, ромб, квадрат. Учитель обращает внимание на то, что прямоугольник, ромб, квадрат — частные виды параллелограмма, поэтому всем придется доказывать, что четырехугольник EFMN — параллелограмм.

Дано: АЕ = ЕB, BF=FC, СМ=МД, ДN=NА.

Доказать: EFMN — параллелограмм.

Вопрос: Для того, чтобы доказать, что EFMN — параллелограмм, что достаточно доказать?

Ответ; параллельность прямых EF и MN, а также ЕN и MF.

Вопрос: Как можно доказать? (или, если не отвечают: Используя какой признак параллельности прямых можно это доказать?).

Ответ: Первый признак параллельности прямых т.к. в других признаках участвуют углы, а в условии задачи об углах ничего не сказано.

Вопрос: В первом признаке параллельности прямых говорятся о трех прямых. Где взять третью прямую?

Ответ: Соединить точки А и С. Получим два треугольника — АВС и АДС.

Вопрос: Какое соотношение известно в этих треугольниках? Или: Чем являются ЕF и MN в  АВС и  АДС?

Ответ; ЕF является средней линией  АВС, ибо АЕ = FВ и ВГ = FC, а MN является средней линией  АДС, т.к. СМ = МД и ДN = NА.

Вопрос: Какой признак средней линии мы знаем?

Ответ: Средняя линия параллельна основанию.

Вопрос: Какой вывод можно сделать о ЕF и MN?

Ответ: ЕF || АС и МN || АС. Значит, по первому признаку параллельности прямых следует, что ЕF || MN.

Аналогично доказывается, что ЕN || FM.

Проведем так называемый «взгляд назад» и попробуем найти другое решение, более рациональное и короткое.

Вопрос: Как еще можно доказать, что четырехугольник EFMN — параллелограмм?

Или: Каким признаком параллелограмма можно воспользоваться, чтобы доказать, что четырехугольник EFMN — параллелограмм?

Ответ: Воспользоваться признаком параллелограмма, который заключается в том, что если в четырехугольнике противоположные стороны попарно параллельны и равны, то этот четырехугольник — параллелограмм. Значит надо доказать, что EF || MN и EF = MN.

Вопрос: Параллельность прямых EF и MN доказывается так, как это было сделано выше. Как доказать равенство ЕF и МN? или: Какое свойство средней линии мы знаем?

Ответ: Так как ЕF — средняя линия  АВС, то ЕF равна половине основания АС; MN средняя линия АДС и М равна половине основания АС. Значит ЕF = MN.

Это решение является более рациональным и коротким.

Теперь надо записать решение задачи. Для этого уже используется синтез.

АЕ = ЕВ ЕF || AC

BF = FC EF = 1/2 AC EF || MN  EFMN – парал–

СМ = МД MN || AC EF = MN лелограмм

ДN = NA MN = 1/2 AC

В классе всегда есть ученики, которые быстро найдут решение этой задачи. Для организации индивидуальной групповой деятельности более сильным учащимся можно дать дополнительные задания:

Какой вид должен иметь исходный четырехугольник, чтобы полученный был

В этом случае целесообразно подойти к распределению дифференцированно: наиболее сильным предложить вариант в), средним — вариант б), остальным — а).

Предлагая учащимся задачи с избыточной и неполной информацией, мы воспитываем в них готовность к практической деятельности. Рассматривая изящное решение той или иной математической задачи, мы способствуем эстетическому воспитанию школьников.
Опыт показывает, что успешность в реализации воспитывающих функций математических задач во многом определяется пробуждением у учащихся интереса к данной задаче, возникновением у них устойчивой потребности в
её решении, наличием интереса к самому процессу решения задач на основе последнего часто возбуждается и формируется интерес учащихся к изучению
самой математики и смежных учебных дисциплин, интерес к учению в целом.
Факторы, существенно влияющие на формирование у учащихся устойчивого
интереса к решению математических задач, весьма разнообразны.

К ним относится доступность предложенной задачи, внешняя или
внутренняя занимательность задачи, осознанная возможность проявить при
этом творческую самостоятельность.

Глава 3. Применение темы « Площадь четырехугольника» к решению задач в ГИА и ЕГЭ.

В своей практической деятельности человек часто имеет дело с площадями. Чтобы найти , например , урожайность с 1 га, надо знать площадь и сколько всего зерна собрано с этого поля. О площади , занимаемой каким- либо государством, узнаем из курса географии. Площадь опоры и поперечного сечения узнаем, решая задачи по физике.

Изучаемые в геометрии фигуры являются отражением реальных форм предметов, с которыми мы постоянно встречаемся в жизни.

Можно сказать , что площадь многоугольника – это величина той части плоскости, которую занимает многоугольник. Измерение площадей проводится с помощью выбранной единицы измерения. За единицу измерения площадей принимают квадрат со стороной 1 см. такой квадрат называется квадратным сантиметром – см 2 . Аналогично определяется квадратный метр ( м 2 ), квадратный миллиметр ( мм 2 ) и т.д.

Как же решаются задачи, связанные с нахождением площадей? Для решения таких задач используется метод площадей. Метод площадей имеет много разновидностей. Его применяют, например, при замене отношения отрезков, расположенных на одной прямой, отношением площадей треугольников с общей вершиной, основаниями которых являются рассматриваемые отрезки. При решение задач используют следующие свойства площадей:

1. Площадь фигуры является положительным числом.
2. Площади равных фигур равны.
3. Если фигура разделена на две части, то площадь всей фигуры равна сумме площадей образовавшихся частей.

Фигуры, имеющие равные площади, называются равновеликими.

При решение задач методом площадей часто используются формулы, выражающие площадь треугольника.

Обозначим, через A, B ,C величины соответствующих углов треугольника ABC, а через a,b,c,как обычно, длины противоположных им сторон, 2p- периметр треугольника, r и R – соответственно радиусы вписанной и описанной окружности.

Для площади треугольника справедливы следующие формулы:

S = 2R 2 sin A sin B sin C,

При решение задач на нахождение площадей четырёхугольников используют формулы соответствующие определенному виду четырехугольников.

Так площадь трапеции равна произведению полусуммы оснований на высоту трапеции S = .

а

Или, площадь равна произведению средней линии на её высоту

А также площадь трапеции можно найти с помощью произведения её диагоналей на синус угла между ними.

Для нахождения площади параллелограмма можно воспользоваться несколькими формулами.

1. Площадь равна произведению его стороны на высоту, опущенную на эту сторону : S = ah a = bh b ;

1. Площадь равна произведению его соседних сторон на синус угла между ними : S = ab ;
2. Площадь равна полупроизведению его диагоналей на синус угла между ними: S = d 1 d 2 .

Для вычисления площади прямоугольника и квадрата используются следующие формулы.

— площадь равна квадрату его сторон S = a 2 .

— площадь равна половине квадрата его диагонали S = d 2 .

— площадь равна произведению его сторон S = ad;

— площадь равна полупроизведению квадрата диагоналей на синус угла между ними S = d 2

Ромб. Его площадь можно найти , если она равна :

— произведению стороны и высоты ромба

— произведению квадрата его стороны на синус угла ромба

-полупроизведению его диагоналей

-удвоенному произведению стороны на радиус окружности, вписанной в ромб S = 2ar.

Рассмотрим опорные задачи , решаемые методом площадей.

Пример 1.Пусть О – точка пересечения диагоналей четырехугольника ABCD. Тогда имеет место равенство = .

Решение. Пусть и h 2 высоты треугольников ABD и CBD, проведенные к стороне BD. Очевидно, что = = = .

C

Пример 2. Стороны параллелограмма 10 см и 6 см, а угол между этими сторонами 150 градусов. Найдите площадь параллелограмма.

Катет АЕ лежит против угла 30 , поэтому = АВ = 3 см.

= BC AE = 10 3 = 30 см 2 .

Пример 3. В треугольнике ABC . На сторонах AC, BC, AB соответственно взяты точки М, Р, К так, что четырехугольник СМРК является квадратом АС =6 см, ВС = 14 см. Найдите сторону МС.

Решение. 1) AC CB = 6 ).

42 = ( 6 – x) (14 – x)

2x 2 + 6x – x 2 + 14x – x 2 = 84

X = 4,2. Ответ: МС = 4,2 см.

Вычислить площадь выпуклого четырехугольника, диагонали которого перпендикулярны, а длины их равны 8 см и 12 см.

Найти площадь равнобокой трапеции, если меньшее основание 18 см, высота 9 см, а острый угол 45 градусов.

Два участка земли огорожены заборами одинаковой длины. Первый прямоугольный участок имеет стороны 220 м и 160 м, а второй имеет форму квадрата. Площадь какого участка больше и на сколько?

Полкомнаты, имеющей форму прямоугольника со сторонами 5,5 м и 6 м, нужно покрыть паркетом прямоугольной формы. Длина каждой дощечки паркета 30 см, а ширина 5 см. Сколько потребуется таких дощечек для покрытия пола?

Дидактический материал на применение метода площадей очень разнообразен. Он направлен на развитие геометрически представлений, выработку умений и навыков нахождения площадей в ходе решения задач. Стали традиционными для ЕГЭ и ГИА по математике задачи на вычисление площади плоской фигуры.

Задание на вычисление площади четырехугольника ( треугольника, круга) представляет собой изображение фигуры, площадь которой требуется найти, на клетчатой бумаге (сетке) со стороной клетки 1.

Площадь искомой фигуры может быть найдена по известной формуле. Например, для параллелограмма во многих случаях достаточно провести мысленно высоту к одной из сторон. Выбирать в качестве стороны и высоты нужно те длины, которые выражаются целыми числом делений сетки. В некоторых случаях для вычисления недостающих элементов можно использовать теорему Пифагора. Ряд задач можно решить, разбив фигуру на части, вычисление площадей которых не представляет труда, или, заметив, что фигура сама является частью другой фигуры, а площадь последней можно найти почти сразу.

Задача. ЕГЭ, 2010г.

Найти площадь квадрата, изображенного на клетчатой бумаге со стороной 1 см. ответ дайте в квадратных сантиметрах.

Решение. Площадь квадрата равна квадрату его стороны, а квадрат стороны в данном случае можно найти по теореме Пифагора, он будет равен 4 2 + 2 2 , т.е.20. Ответ: 20см 2 .

На клетчатой бумаге с клетками размером 1 см 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах

Задача. ЕГЭ, ДЕМО 2012Г.

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см. Ответ дайте в квадратных сантиметрах.

В 2009годудля ЕГЭ по математике использовались задачи на вычисление площади фигуры расположенной на координатной плоскости.

Найдите площадь четырехугольника, вершины которого имеют координаты (2;7), (10;5), (10;8), (2;10)

Найдите площадь четырехугольника, вершины которого имеют координаты (2;7), (6;6), (6;9), (2;10).

Найдите площадь четырехугольника, вершины которого имеют координаты (2;7), (8;6), (8;9), (2;10).

Приложение по теме « Четырехугольники».

В процессе обучения важное место отводится организации повторения изученного материала. Необходимость повторения обусловлена задачами обучения, требующие прочного и сознательного овладения ими.

Указывая на важность процесса повторения и обобщения изученного материала, современные исследователи показали значительную роль при этом таких дидактических приемов, как сравнение, классификация, анализ, синтез, обобщение, содействующие интенсивному протеканию процесса запоминания.

Для этих целей можно использовать тесты, которые являются итоговой формой диагностики знаний учащихся при завершении каждой темы курса.

Т ест по теме « Четырехугольники».

1 .Параллелограмм – это четырехугольник , у которого …

а)… противоположные стороны равны;

б)… противоположные углы равны;

в)… противоположные стороны параллельны.

2 . Что означает следующая формула Р = 2( a + b)

а) периметр трапеции равен удвоенной сумме сторон,

б) периметр ромба равен сумме сторон,

в) периметр прямоугольника равен удвоенной сумме соседних сторон.

3 . Вписанный четырехугольник – это…

а) …, у которого суммы пар противоположных углов равны 180 градусов;

б) …, все вершины которого не принадлежат данной окружности;

в) …, каждая сторона которой касается данной окружности.

4 .Укажите на рисунке равнобокую трапецию.

а) б) в)

1. Найти углы ромба , если его диагонали составляют с его стороной углы, один из которых на 30градусов меньше другого.

6. Средняя линия трапеции равна 30, а меньшее основание равно 20. Найдите большее основание трапеции.

а) 40 , б) 20, в) 60.

7 . Укажите на рисунке вписанный прямоугольник.

8 .Угол А четырехугольника ABCD вписанного в окружность, равен 100 . Найти угол С.

а) 80 . б) 70, в) 60.

9 .Площадь какой фигуры вычисляется по формуле S = a b.

а) ромб, б) квадрат , в) прямоугольник.

10 . Основания трапеции равны 10 и 35 , площадь равна 225. Найти ее высоту.

1 .Ромб – это параллелограмм, у которого …

а) … противоположные углы равны,

б) … диагонали являются биссектрисами его углов ,

в) … все стороны равны.

2 . Что означает следующая формула d 2 = a 2 + b 2 .

а) сумма квадратов двух сторон равна квадрату диагонали трапеции,

б) квадрат диагоналей прямоугольника равен сумме квадратов двух соседних сторон ,

в) квадрат суммы диагоналей равен квадрату высот трапеции.

3. Описанный четырехугольник – это четырехугольник …

а) …, у которого сумма противоположных углов равна 180 градусов,

б) …, у которого суммы длин противоположных сторон равны,

в) …, у которого сумма углов равна 360 градусов.

4 .Укажите на рисунке прямоугольную трапецию.

а) б) в)

5 .В ромбе ABCD биссектриса угла BAC пересекает сторону ВС и диагональ BD соответственно в точках M и N.Найти угол ANB, если угол АМС равен 120 .

а)120 , б) 100 , в)110 .

6 . В прямоугольной трапеции один из углов равен 45 ,средняя линия = 24, основания относятся как 3:5. Найти меньшую боковую сторону трапеции.

а) 18. б) 24 , в) 12.

7 .Укажите на рисунке описанный четырехугольник.

а) б) в)

8 .В четырехугольник ABCD вписана окружность .АВ равна 11, CD = 17. Найти периметр четырехугольника.

9 .Площадь какой фигуры вычисляется по следующей формуле

а ) трапеция , б) квадрат, в) прямоугольник.

10 . Основания трапеции равны 10 и 35 , площадь равна 225. Найти ее высоту.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Четырёхугольники. Творческая работа по теме.

Цель: 1). Систематизировать знания по данной теме.

2). Ещё раз повторить все определения, свойства и признаки фигур.

3). Показать их применение к решению задач.

4). Подвести итоги творческой работы по данной теме.

Для более результативной работы разбиваем класс на пять групп, подразумевается, что класс уже умеет работать в группах. Группа №1- параллелограммы; №2 – прямоугольники; №3 – ромбы; №4 – квадраты.

В начале урока предлагаются задачи для устного решения, на применение определений, свойств и признаков фигур. Каждая группа может заработать жетон — очко за решённую задачу, дополнение, исправление

ошибок в ответах товарищей. В конце занятия, группе получившей большее количество жетонов присваивается звание — «Знатоки четырёхугольников».

I. этап: устная разминка;

II. этап: повторение свойств, признаков и определений фигур;

III. этап: решение задач, защита решения;

IV. этап: подведение итогов, рассматриваем лучшие творческие работы.

А. Дан четырёхугольник АМС D . Докажите,

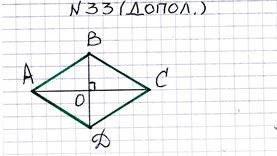
что АМС D – ромб.

Докажите, что четырёхугольник АМСК,

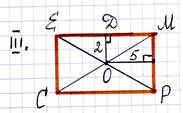
EMPC – прямоугольник, найдите периметр

В. Повторяем определения, свойства и признаки фигур.

(учащиеся показывают инсценировку)

Ученик Вася; Геометрические фигуры: параллелограмм, ромб, прямоугольник, квадрат.

В некоторой школе,

Да в восьмом уж классе,

Был способный ученик,

Он геометрии учился,

Знал доказательств остроту,

Но после лета обленился

И как-то раз попал в беду.

Итак, Василий, расскажи

О свойствах всех квадрата,

И на рисунке покажи

Фигура чем богата?

В а с я: (водит по чертежу указкой)

Ох, я, не знаю, Марь Петровна,

Болела сильно голова!

И не нашел я эти свойства.

Садись, Василий, снова два!

Ставит оценку в дневник.

А ночь тебе, дружок, не спать,

Зачётик завтра, срочно сдать!

Пришел, Василий наш домой,

С досадой сумку пнул,

Учебник взял и сел учить,

О, господи! Заснул!

И снится Васе сущий ад!

Как будто он — больной квадрат.

К в а д р а т (входит охая, голова перевязана):

Я несчастный квадрат,

Нету свойств у меня,

Среди белого дня!

Я и жить не хочу!

Ах, какие мучения!

Где же свойства мои

Вбегают ромб, прямоугольник, параллелограмм входит, хромая,

опираясь на линейку.

Что случилось, брат-квадрат?

Почему ты нам не рад?

Свойства все мои украли,

Так что жить я не хочу!

Что ты, квадрушка, постой!

Ты же братец наш родной,

Всем, что есть у нас в запасе,

Мы поделимся с тобой.

Вот я ромб – такой параллелограмм,

Что у меня все стороны равны,

И я тебе сейчас же их отдам,

Родные и друзья делиться всем должны.

А еще, квадратик! Знай же ты о том,

Мои диагонали под прямым углом.

И еще сказать вам я, друзья, готов.

Они ведь биссектрисы всех моих углов.

Эти чудо — свойства я тебе дарю,

Ну, а за внимание всех благодарю.

П р я м о у г о л ь н и к:

А я прямоугольник, такой параллелограмм

С прямыми, брат, углами

Тебе я их отдам.

Диагоналей свойство позволь тебе вручить!

Они равны, двойняшки. Их можно начертить.

П а р а л л е л о г р а м м:

Расступись, ребята. Дедушке два слова!

Буду рад я видеть наш квадрат здоровым.

Вы меня узнали — я параллелограмм,

Свое определение расскажу я вам.

Я старый и хромой, и с рифмой не в ладах.

Вот определение, но только не в стихах!

Я — параллелограмм, такой четырехугольник у которого противоположные стороны параллельны.

А свойства все мои, отдал я вам давно,

Напомним их, ребята, квадрату заодно!

Мои диагонали, раз я параллелограмм,

Пересеченья точкой разделим пополам.

Если сторона одна, да напротив то другой,

То они всегда равны — это уж само собой.

Если угол то один, а напротив то другой,

То они всегда равны — это уж само собой.

А теперь вы мне скажите,

Как в толпе друзей, родных

Меня, деда, отличите

От фигур вы остальных?

П р я м о у г о л ь н и к:

Знаем, признак существует,

По которому тот час,

Мы тебя узнаем мигом

Среди всех похожих нас.

Вы спросите любого школьника,

Он ответит сразу же вам:

«Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — па раллелограмм».

П а р а л л е л о г р а м м:

А еще, мои внучата,

Я хочу всем рассказать,

Что второй имею признак

Его тоже нужно знать:

Если две стороны четырехугольника

Параллельны и равны,

То перед вами я — ваш дедушка,

Вы сомневаться не должны!

Ну, квадратик, как дела?

К в а д р а т: (снимает повязку с головы)

Голова моя цела,

И в душе волнение!

Спасибо вам, друзья, за все

Ведь вы — мое спасение.

Вернулись свойства все ко мне

Я — прямоугольник, стороны равны,

Еще раз убедился, как вы мне нужны!

Проснулся наш Василий,

Ушел от страшных снов,

И вдруг как осенило: К зачету ведь готов!

Спасибо вам, фигуры,

Дорога в геометрии

Не будет больше двоек,

Их стыдно получать.

Я твердо обещаю

Зачет отлично сдать!

У ребят, исполняющих роли геометрических фигур, соот ветствующие фигуры из картона прикреплены на груди. У всех фигур, кроме квадрата отмечены их свойства и равные элементы. На голову можно сделать четырехугольные шапочки с кисточками. Когда фигуры дарят свои свойства квадрату, они толстым фломастером отмечают их на изображении квадрата, который находится на груди ученика.

С. Хорошее получилось повторение. Спасибо ребятам. Переходим к решению задач.

Дано: АВС D – параллелограмм, АЕ биссектриса угла А, АЕ ∩ ВС в точке Е, АВ=9см, AD =15см

Дано: ABCD – четырёхугольник,

Доказать: ABCD параллелограмм

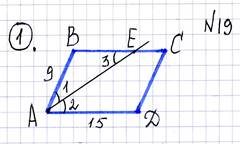
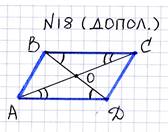
Дано: ABCD – прямоугольник, МО ABCD равен 56см

Найдите : AB, BC, CD, AD

Дано: ABCD — параллелограмм, ∟ A =∟ B = ∟ C =∟ D

Доказать: ABCD прямоугольник

Дано: ABCD параллелограмм, AC ⊥ BD

Доказать: ABCD ромб

Группа квадратов:

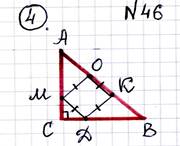
Дано: ∆ АВС – прямоугольный, ∠ С=90 º , АС=СВ,

МОК D – квадрат, АВ=3м

Найти: ОК – сторону квадрата

Дано: ABCD – прямоугольник, АС ⊥ BD

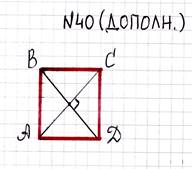
Доказать: ABCD квадрат

D . Защита задач, опрос в группах по четырёхугольникам. Подведение итогов.

Е. Представление лучших творческих работ.

«Пропавшие братья» — геометрический детектив,

автор Каширская Лена 8б (приложение №3);

«Легенда о создании прямоугольника, ромба и квадрата»

Автор Белякова Вика 8б и т.д.

Домашнее задание: повторить теоретический материал, №32, 37.

Видео:Четырехугольники. Вебинар | МатематикаСкачать

Задания, карточки, проблемные вопросы по теме: «Четырехугольники»

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Применение способа диалектического обучения в учебном процессе обеспечивает развитие познавательных универсальных учебных действий, что ведет к формированию способности самостоятельно успешно усваивать новые знания, овладевать предметными и общими умениями, включая самостоятельную организацию процесса учения, т.е. умение учиться.

Познавательные УУД включают в себя умения:

— общеучебные , использующие элементарные учебные умения (чтение, письмо, счет) и развивающие способность работать с текстом, другими источниками информации;

— логические , формирующие мыслительные способности;

— действия постановки и решения проблем , связанные с выявлением противоречий в содержании материала, с поиском путей их решения.

Предложенные ниже предметные задания и карточки, способствующие усвоению информации, содержащейся в учебном материале и тексте, разработаны в соответствии с развиваемыми универсальными умениями.

Система заданий по математике к теме «Четырехугольники».

Учебник (полные библиографические данные): Геометрия, 7-9. Л.С. Атанасян и др.. М: Просвещение, 2015г.

Сформулируйте проблемные вопросы к теме урока «Параллелограмм», которые будут отражать цель урока.

— Что называется параллелограммом?

— Каким образом параллелограммы отличаются от других геометрических фигур?

— Каковы свойства и виды параллелограммов?

Отличать параллелограмм от других фигур.

Указывать существенные признаки прямоугольника, ромба, квадрата.

Анализ объектов с целью выделения признаков (сущ.и несущ.).

Осознанное и произвольное построение речевого высказывания в устной и письменной форме.

Тема урока: «Трапеция». Предположите, на какие вопросы-понятия необходимо ответить, чтобы построить алгоритм действий на уроке, который позволит отразить цель урока.

— Что считается трапецией?

— Каковы виды трапеций и их свойства?

-В чем заключается отличие трапеции от параллелограмма?

Отличать трапецию от других фигур.

Указывать существенные признаки трапеции, прямоугольной и равнобедренной трапеций.

Анализ объектов с целью выделения признаков (сущ.и несущ.).

Осознанное и произвольное построение речевого высказывания в устной и письменной форме.

Прочитав текст §3 ответить на вопросы-понятия по теме «Прямоугольник. Квадрат. Ромб.»

-Что называются прямоугольником?

-Что считается квадратом?

— Что понимается под фигурой ромб?

-Что представляет собой прямоугольник и квадрат?

-Что является ромбом и квадратом?

-Какова сумма углов данных многоугольников?

— Каковы общие свойства прямоугольника, ромба, квадрата?

-В чем заключаются особые свойства ромба?

Определять существенные признаки квадрата, прямоугольника, ромба.

Анализ объектов с целью выделения признаков (сущ.и несущ.).

Осознанное и произвольное построение речевого высказывания в устной и письменной форме.

Выписать из §2 учебника содержание и объем понятия «параллелограмм».

1.по соотношению величин сторон: квадрат, ромб; прямоугольник.

2.по соотношению величин углов: квадрат, прямоугольник; ромб.

Определять существенные признаки параллелограмма, квадрата, прямоугольника, ромба.

Анализ объектов с целью выделения признаков (сущ. и несущ.).

Осознанное и произвольное построение речевого высказывания в устной и письменной форме.

Прочитав выражения, установить, какие из них являются определением понятия, и доказать свою точку зрения:

Квадрат – это прямоугольник.

Прямоугольник – это параллелограмм, у которого все углы прямые.

Первое выражение не является определением понятия «квадрат», т.к. не смотря на то, что указан родовой признак (прямоугольник), и он истинный, нет видовых признаков.

Второе выражение является определением понятия «прямоугольник», т.к. есть родовой признак «параллелограмм», являющийся истинным и видовой признак «у которого все углы прямые», тоже являющийся истинным.

Видовой признак отражает строение прямоугольника, поэтому определение является структурным.

Определя ют существенные признаки квадрата и прямоугольника.

Устанавлива ют истинность признаков, принадлежащих квадрату и прямоугольнику.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Осуществля ют подведение под понятие.

Стро ят логическую цепь рассуждений и доказательство.

Осознанно и произвольно стро ят речевое высказывание в устной и письменной форме

Восстановить пропущенные элементы в определениях понятий:

1. Параллелограмм – это…, у которого … стороны….параллельны.

Пропущенные понятия: четырехугольник, противоположные, попарно.

2. Трапеция – это… , у которого … стороны…,а…стороны… параллельны.

Пропущенные понятия: четырехугольник, две, параллельны, две другие, не.

Восстанавливаем первое понятие с помощью пропущенных элементов. Получаем: параллелограмм-это четырёхугольник, у которого противоположные стороны попарно параллельны.

Второе определение: трапеция-четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Определя ют существенные признаки параллелограмма и трапеции.

Устанавлива ют истинность признаков, принадлежащих параллелограмму и трапеции.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Осуществля ют подведение под понятие.

Стро ят логическую цепь рассуждений и доказательство.

Осознанно и произвольно стро ят речевое высказывание в устной и письменной форме

Выбрать из перечисленных свойств только те, которые являются существенными признаками всех параллелограммов:

четырехугольник, равные углы, прямые углы, диагонали, попарно равные стороны, параллельные стороны, попарно равные углы, середина диагоналей, перпендикулярные диагонали, равные диагонали, диагонали, делящиеся пополам, вершины, противоположные стороны.

Назвать среди указанных признаков родовой и видовые признаки параллелограммов. Сформулировать определение параллелограмма, используя выделенные признаки.

Постоянными признаками всех параллелограммов являются: четырехугольник, попарно равные стороны, параллельные стороны, попарно равные углы, середина диагоналей, диагонали, делящиеся пополам, вершины, противоположные стороны.

Параллелограмм- это четырехугольник, у которого противоположные стороны попарно параллельны.

Родовой признак – четырехугольник – истинный; истинные видовые признаки – противоположные стороны попарно параллельны.

Распознаютсущественные и несущественные признаки параллелограммов.

Формулируют определения понятия «параллелограмм»

Устанавлива ют истинность признаков, принадлежащих параллелограммам.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Осуществляют синтез как составление целого из частей.

Осуществля ют подведение под понятие.

Стро ят логическую цепь рассуждений и доказательство.

Осознанно и произвольно стро ят речевое высказывание в устной и письменной форме

В определениях понятий указать родовой и видовые признаки, установить их истинность.

Четырехугольник- многоугольник, состоящий из четырех точек плоскости, попарно соединенных отрезками.

Ромб-это параллелограмм, у которого все стороны равны.

Родовой признак понятия «четырехугольник» – многоугольник, но он ложный(выпуклый многоугольник); видовые признаки – состоящий из четырех точек плоскости, попарно соединенных отрезками-истинный. Следовательно, это определение не является истинным определением понятия «четырехугольник». Истинное определение « Четырехугольник-это выпуклый многоугольник, состоящий из четырех точек плоскости, попарно соединенных отрезками».

Родовой признак понятия «ромб» — параллелограмм (он истинный); видовой признак – все стороны равны (истинный). Значит, это определение является истинным определением понятия «ромб».

Распозна ют существенные и несущественные признаки четырехугольника и ромба.

Формулиру ют определения понятия «четырехугольник», «ромб».

Устанавлива ют истинность признаков, принадлежащих четырехугольнику и ромбу.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Осуществля ют подведение под понятие.

Стро ят логическую цепь рассуждений и доказательство.

Осознанно и произвольно стро ят речевое высказывание в устной и письменной форме

Отметить знаком «+» правильные определения понятий и знаком «-» неправильные.

Распозна ют существенные и несущественные признаки понятия «Параллелограмм»

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Стро ят логическую цепь рассуждений и доказательство.

Осознанно и произвольно стро ят речевое высказывание в устной и письменной форме.

Найти основание деления понятий выпуклый и невыпуклый четырехугольники

выпуклый и невыпуклый четырехугольники делятся по расположению на плоскости относительно каждой прямой, проходящей через две его соседние вершины.

Распознают выпуклый и невыпуклые четырехугольники по существенному признаку

Анализ объектов с целью выделения признаков (сущ. и несущ.).

Выбор оснований и критериев для сравнения, сериации, классификации объектов.

Установление причинно-следственных связей

Осознанное и произвольное построение речевого высказывания в устной и письменной форме.

Умение структурировать знания

Найти виды понятий по указанным критериям

1.четырехугольники- по параллельности противоположных сторон

2.четырехугольники- по расположению на плоскости относительно каждой прямой, проходящей через две его соседние вершины

не параллелограмм (по параллельности противоположных сторон)

выпуклый, невыпуклый (по расположению на плоскости относительно каждой прямой, проходящей через две его соседние вершины)

Распознают параллелограмм, не параллелограмм, выпуклый и невыпуклые четырехугольники по существенному признаку

Анализ объектов с целью выделения признаков (сущ.и несущ.).

Выбор оснований и критериев для сравнения, сериации, классификации объектов.

Установление причинно-следственных связей

Осознанное и произвольное построение речевого высказывания в устной и письменной форме.

Умение структурировать знания

Установить соответствие между видами параллелограммов и их признаками

Распознают существенные признаки понятий: квадрат, прямоугольник, ромб.

Анализ объектов с целью выделения признаков (сущ.и несущ.).

Выбор оснований и критериев для сравнения, сериации, классификации объектов.

Установление причинно-следственных связей

Осознанное и произвольное построение речевого высказывания в устной и письменной форме.

Умение структурировать знания

Найти лишнее понятие, указав основание деления

Лишнее понятие — трапеция( D ), т.к. этот четырехугольник не является параллелограммом, а квадрат, прямоугольник, ромб – это параллелограммы (по параллельности противоположных сторон)

Распознают существенные признаки понятий: квадрат,прямоугольник, ромб, трапеция

Анализ объектов с целью выделения признаков (сущ.и несущ.).

Выбор оснований и критериев для сравнения, сериации, классификации объектов.

Установление причинно-следственных связей

Осознанное и произвольное построение речевого высказывания в устной и письменной форме.

Умение структурировать знания

Назвать признаки, на основании которых можно сравнить понятия: ромб,квадрат

Принадлежность к параллелограммам

Количество сторон, вершин

Определяют существенные признаки, на основании которых можно сравнить ромб и квадрат

Анализ объектов с целью выделения признаков (сущ.и несущ.).

Выбор оснований и критериев для сравнения, сериации, классификации объектов.

Установление причинно-следственных связей

Осознанное и произвольное построение речевого высказывания в устной и письменной форме.

Умение структурировать знания

Обобщить понятие ромб до ближайшего рода.

Распознают существенные признаки ромба, параллелограмма

Анализ объектов с целью выделения признаков (сущ.и несущ.).

Подведение под понятие.

Установление причинно-следственных связей

Осознанное и произвольное построение речевого высказывания в устной и письменной форме.

Умение структурировать знания

Ограничить до ближайшего вида понятие параллелограмм

Называют вид параллелограмма

Анализ объектов с целью выделения признаков (сущ.и несущ.).

Подведение под понятие.

Установление причинно-следственных связей

Осознанное и произвольное построение речевого высказывания в устной и письменной форме.

Умение структурировать знания

Восстановить пропущенные звенья в цепочке :геометрическая фигура -…. –прямоугольник АВСД.

Геометрическая фигура→ плоская фигура→выпуклый многоугольник→ четырехугольник→параллелограмм→прямоугольник→прямоугольник АВСД

Определяют геометрическую фигуру, плоскую фигуру, выпуклый многоугольник,четырехугольник,параллелограмм, прямоугольник по существенным признакам

Анализ объектов с целью выделения признаков (сущ.и несущ.).

Подведение под понятие.

Установление причинно-следственных связей

Осознанное и произвольное построение речевого высказывания в устной и письменной форме.

Умение структурировать знания

Отразите отношения между понятиями с помощью кругов Эйлера.

А-ромб со стороной 5 см

В-ромб с диагоналями 6см, 8 см

Определяют ромб по существенным признакам

Анализ объектов с целью выделения признаков (сущ. и несущ.).

Синтез как составление целого из частей, в том числе самостоятельное достраивание, восполнение недостающих компонентов.

Установление причинно-следственных связей

Знаково-символические действия, включая моделирование.

Умение структурировать знания

Отразите отношения между понятиями с помощью кругов Эйлера

А-ромб, В-прямоугольник, С-квадрат

Распознают ромб, квадрат, прямоугольник по существенным признакам

Анализ объектов с целью выделения признаков (сущ.и несущ.).

Синтез как составление целого из частей, в том числе самостоятельное достраивание, восполнение недостающих компонентов.

Установление причинно-следственных связей

ОУ ПУУД:

Знаково-символические действия, включая моделирование.

Умение структурировать знания

Отразите отношения между понятиями с помощью кругов Эйлера

Распознают параллелограмм, квадрат по существенным признакам

Анализ объектов с целью выделения признаков (сущ.и несущ.).

Синтез как составление целого из частей, в том числе самостоятельное достраивание, восполнение недостающих компонентов.

Установление причинно-следственных связей

Знаково-символические действия, включая моделирование.

Умение структурировать знания

Отразите отношения между понятиями с помощью кругов Эйлера

Определяют четырехугольники, параллелограмм, трапецию по существенным признакам

Анализ объектов с целью выделения признаков (сущ.и несущ.).

Синтез как составление целого из частей, в том числе самостоятельное достраивание, восполнение недостающих компонентов.

Установление причинно-следственных связей

Знаково-символические действия, включая моделирование.

Умение структурировать знания

Отразите отношения между понятиями с помощью кругов Эйлера

С-тупой угол

Распознают острый,прямой, тупой углы по существенным признакам

Анализ объектов с целью выделения признаков (сущ.и несущ.).

Синтез как составление целого из частей, в том числе самостоятельное достраивание, восполнение недостающих компонентов.

Установление причинно-следственных связей

Знаково-символические действия, включая моделирование.

Умение структурировать знания

Отразите отношения между понятиями с помощью кругов Эйлера

Распознают выпуклый, невыпуклый четырехугольники по существенным признакам

Анализ объектов с целью выделения признаков (сущ.и несущ.).

Синтез как составление целого из частей, в том числе самостоятельное достраивание, восполнение недостающих компонентов.

Установление причинно-следственных связей

Знаково-символические действия, включая моделирование.

Умение структурировать знания

Отразите отношения между понятиями с помощью кругов Эйлера

Распознают выпуклый, невыпуклый многоугольники по существенным признакам

Анализ объектов с целью выделения признаков (сущ.и несущ.).

Синтез как составление целого из частей, в том числе самостоятельное достраивание, восполнение недостающих компонентов.

Установление причинно-следственных связей

Знаково-символические действия, включая моделирование.

Умение структурировать знания

1. Определить структуру суждения, выделив субъект и предикат мысли:

Крышка стола имеет форму прямоугольника.

2. Установить, какие предложения являются суждениями, доказать свою точку зрения:

Некоторые параллелограммы являются прямоугольниками.

Они имеют прямые углы.

3. В форме суждения ответить на вопрос-понятие:

Что представляет собой крышка стола?

Крышка стола – субъект, форма прямоугольника – это предикат, связкой является слово «имеет».

Некоторые параллелограммы являются прямоугольниками. Это суждение, т.к. субъектом является некоторые параллелограммы, а предикатом – прямоугольниками. Связка – являются.

Они имеют прямые углы.

Это не суждение, т.к. нет субъекта.

Крышка стола представляет собой многоугольник, который является прямоугольником.

Распознают понятия прямоугольник, параллелограмм, прямой угол

Осознанно и произвольно строят речевое высказывание в устной и письменной форме.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Осуществля ют подведение под понятие.

Стро ят логическую цепь рассуждений и доказательство.

Сформулировать суждение на сравнение параллелограмма и трапеции, выделив их общие признаки.

Так же, как и параллелограмм, трапеция является выпуклым четырехугольником.

Как параллелограмм, так и трапеция может иметь прямой угол.

Сравнивают параллелограмм и трапецию по существенным признакам.

Осознанно и произвольно строят речевое высказывание в устной и письменной форме.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Выбор оснований и критериев для сравнения, сериации, классификации объектов. Стро ят логическую цепь рассуждений и доказательство.

Сформулировать суждения на сравнение параллелограмма и трапеции, выделив их особенные признаки.

Если для нахождения площади параллелограмм используем одну сторону и высоту, проведенную к ней, то для нахождения площади трапеции используем две параллельные стороны и высоту, проведенную между ними.

В отличие параллелограмма, не всякую трапецию можно разделить на два равных треугольника.

Сравнивают параллелограмм и трапецию по существенным признакам.

Осознанно и произвольно строят речевое высказывание в устной и письменной форме.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Выбор оснований и критериев для сравнения, сериации, классификации объектов. Стро ят логическую цепь рассуждений и доказательство.

Составить карточку №3, сравнив параллелограмм и трапецию.

1.По сравнению с параллелограммом все стороны, которого попарно параллельны, у трапеции только две стороны параллельны.

2.Так же, как и параллелограмм, трапеция является выпуклым четырехугольником.

Как параллелограмм, так и трапеция может иметь прямой угол.

Сравнивая параллелограмм с трапецией, можно сказать , что они являются четырехугольниками.

Кроме параллелограмма, ещё и трапеция имеет диагонали.

Помимо параллелограммов, окружающие нас фигуры имеют форму трапеции.

Параллелограмм имеет больше видов, чем трапеция (трапеция: равнобедренная, прямоугольная; параллелограмм: прямоугольник, квадрат, ромб)

Не только параллелограмм, а и трапеция имеет площадь и периметр.

Наряду с параллелограммом, и трапецию можно разделить на два треугольника.

Если для нахождения площади параллелограмм используем одну сторону и высоту, проведенную к ней, то для нахождения площади трапеции используем две параллельные стороны и высоту, проведенную между ними.

В отличие от параллелограмма, трапецию нельзя разделить на два равных треугольника.

Сравнивают параллелограмм и трапецию по существенным признакам.

Осознанно и произвольно строят речевое высказывание в устной и письменной форме.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Выбор оснований и критериев для сравнения, сериации, классификации объектов. Стро ят логическую цепь рассуждений и доказательство.

В строке выделить сравнимые понятия, обосновать свой выбор:

квадрат, прямоугольник, окружность, трапеция, призма.

Среди понятии ( квадрат, прямоугольник, окружность, трапеция, призма ) сравнимыми являются квадрат, прямоугольник, трапеция, т.к. они имеют общий существенный признак — выпуклый четырехугольник .

Определяют общие признаки квадрата, прямоугольника, окружности, трапеции, призмы.

Осознанно и произвольно строят речевое высказывание в устной и письменной форме.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Выбор оснований и критериев для сравнения, сериации, классификации объектов. Стро ят логическую цепь рассуждений и доказательство.

Найдите признаки, по которым можно сравнивать понятия: параллелограмм и трапеция.

Параллелограмм и трапецию можно сравнить по величине наибольшего угла, по параллельности сторон, по величине площади и периметра, по длине сторон, по видам.

Сравнивают параллелограмм и трапецию по существенным признакам.

Осознанно и произвольно строят речевое высказывание в устной и письменной форме.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Выбор оснований и критериев для сравнения, сериации, классификации объектов. Стро ят логическую цепь рассуждений и доказательство.

Определить вид умозаключений, доказать свою точку зрения:1 .Прямоугольник имеет четыре стороны, четыре угла, две диагонали.

Квадрат имеет четыре стороны, четыре угла, две диагонали.

Ромб имеет четыре стороны, четыре угла, две диагонали.

Прямоугольник, квадрат, ромб – параллелограммы.

Параллелограмм – имеет четыре стороны, четыре угла, две диагонали.

Все умозаключения, в которых мысль движется от частного к общему, считаются индуктивными умозаключениями. В данном умозаключении мысль движется от частного (прямоугольник, квадрат, ромб) к общему (параллелограммы).

Следовательно, данное умозаключение являектся индуктивным.

Определяют существенные признаки параллелограмма, ромба, квадрата, прямоугольника.

Умение структурировать знания. Осознанно и произвольно строят речевое высказывание в устной и письменной форме.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Подведение под понятие. Установление причинно-следственных связей. Стро ят логическую цепь рассуждений и доказательство. Выдвижение гипотез и их обоснование.

2.По данным посылкам сформулировать вывод умозаключений:

Все параллелограммы- выпуклые четырехугольники.

Все параллелограммы — выпуклые четырехугольники.

Ромб – выпуклый четырехугольник .

Определяют существенные признаки параллелограмма, ромба, квадрата, прямоугольника.

Умение структурировать знания. Осознанно и произвольно строят речевое высказывание в устной и письменной форме.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Подведение под понятие. Установление причинно-следственных связей. Стро ят логическую цепь рассуждений и доказательство. Выдвижение гипотез и их обоснование.

Восстановить пропущенные посылки в умозаключении:

Прямоугольник имеет равные противоположные стороны, равные противоположные углы, диагонали, точкой пересечения делящиеся пополам.

Квадратимеет равные противоположные стороны , равные противоположные углы , диагонали, точкой пересечения делящиеся пополам.

Ромб имеет равные противоположные стороны , равные противоположные углы , диагонали, точкой пересечения делящиеся пополам.

Параллелограмм имеет равные противоположные стороны, равные противоположные углы, диагонали, точкой пересечения делящиеся пополам.

Прямоугольник имеет равные противоположные стороны, равные противоположные углы, диагонали, точкой пересечения делящиеся пополам.

Квадратимеет равные противоположные стороны , равные противоположные углы , диагонали, точкой пересечения делящиеся пополам.

Ромб имеет равные противоположные стороны , равные противоположные углы , диагонали, точкой пересечения делящиеся пополам.

Прямоугольник, квадрат, ромб – параллелограммы.

Параллелограмм имеет равные противоположные стороны, равные противоположные углы, диагонали, точкой пересечения делящиеся пополам.

Определяют существенные признаки параллелограмма, ромба, квадрата, прямоугольника.

Умение структурировать знания. Осознанно и произвольно строят речевое высказывание в устной и письменной форме.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Подведение под понятие. Установление причинно-следственных связей. Стро ят логическую цепь рассуждений и доказательство. Выдвижение гипотез и их обоснование.

Прочитав § 37 (8 класс) сформулировать два дедуктивных умозаключения.

1.Все параллелограммы- выпуклые четырехугольники.

Ромб – выпуклый четырехугольник.

2.Все прямоугольники – параллелограммы.

Определяют существенные признаки параллелограмма, ромба, квадрата, прямоугольника.

Умение структурировать знания. Осознанно и произвольно строят речевое высказывание в устной и письменной форме.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Подведение под понятие. Установление причинно-следственных связей. Стро ят логическую цепь рассуждений и доказательство. Выдвижение гипотез и их обоснование.

Проверить правильность формулировки умозаключений.

В четырехугольнике АВСД противоположные стороны равны и параллельны, противоположные углы равны, диагонали точкой пересечения делятся пополам.

В четырехугольнике МКРН противоположные стороны равны и параллельны, противоположные углы равны.

В четырехугольнике МКРН диагонали точкой пересечения делятся пополам.

Умозаключение верное. Умозаключение аналогия свойств.

Определяют существенные признаки параллелограмма, ромба, квадрата, прямоугольника.

Умение структурировать знания. Осознанно и произвольно строят речевое высказывание в устной и письменной форме.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Подведение под понятие. Установление причинно-следственных связей. Стро ят логическую цепь рассуждений и доказательство. Выдвижение гипотез и их обоснование.

Установить пропущенные понятия в высказывании: «В планиметрии выделяют шесть видов выпуклых четырехугольников: …, параллелограмм. квадрат, ромб, … .»

В планиметрии выделяют шесть видов четырехугольников : произвольный , параллелограмм, прямоугольник , квадрат, ромб, трапеция .

Осознанно и произвольно строят речевое высказывание в устной и письменной форме.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Синтез, как составление целого из частей. Стро ят логическую цепь рассуждений и доказательство.

Прочитав текст §2 « Параллелограмм и трапеция» выписать признаки параллелограммов.

Признаками параллелограммов являются: выпуклость, параллельность противоположных сторон, равенство противоположных сторон, равенство противоположных углов, деление диагоналей точкой пересечения пополам, деление диагональю на два равных треугольника.

Осознанно и произвольно строят речевое высказывание в устной и письменной форме. Поиск и выделение необходимой информации.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Синтез, как составление целого из частей. Стро ят логическую цепь рассуждений и доказательство.

Изучив содержание § 1 «Многоугольники», указать, на основании каких значимых признаков выделены многоугольники

Ответы: 1.-количество углов, 2-параллельность противоположных сторон, 3- расположение относительно прямой, проходящей через любую сторону, 4-все углы прямые, 5- все стороны равны.

Осознанно и произвольно строят речевое высказывание в устной и письменной форме. Поиск и выделение необходимой информации.

Анализиру ют объекты с целью выделения признаков (сущ., несущ.).

Синтез, как составление целого из частей. Стро ят логическую цепь рассуждений и доказательство.

Указать существенные признаки данной геометрической фигуры. Сформулировать вопрос-суждение, овеет на который позволить отнести данную фигуру к определенному виду. Ответить на него в форме умозаключения.

🔥 Видео

ЧЕТЫРЕХУГОЛЬНИК 8 класс РЕШЕНИЕ ЗАДАЧ АтанасянСкачать

Подготовка к контрольной работе. Четырехугольники. Геометрия 8 класс.Скачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

ЧетырехугольникиСкачать

Как правильно решить задание про четырёхугольник? / Разбор заданий на ОГЭ по геометрииСкачать

Математика 5 класс (Урок№29 - Четырёхугольники.)Скачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Геометрия 10 класс (Урок№2 - Четырехугольники.)Скачать

Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

ЧЕТЫРЕХУГОЛЬНИК и его элементы. §1 геометрия 8 классСкачать

Четырехугольники №1 в ЕГЭ | Профильная математика ЕГЭ 2024 | УмскулСкачать

Задача про четырёхугольник - задание из ОГЭСкачать

Четырехугольники на ЕГЭ - bezbotvyСкачать

Геометрия 8. Урок 13 - Площадь четырехугольников. ЗадачиСкачать

ЧЕТЫРЕХУГОЛЬНИК сложные задачи 8 класс АтанасянСкачать