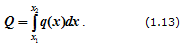Распределенная нагрузка по треугольнику

Видео:Распределенная нагрузкаСкачать

Расчеты в режиме online

Видео:Балка с линейно распределенной нагрузкойСкачать

1.5. Треугольная распределенная нагрузка

Построить эпюры поперечных сил и изгиба­ющих моментов для балки, нагруженной распределенной по закону треугольника нагрузкой, если величина максимальной интенсивности нагрузки равна p₀ = 20 кН/м (рис. 1.13).

Решение. Определим опорные реакции балки, для чего заменим распределенную нагрузку сосредоточенной силой Fc, прило­женной в центре тяжести треугольника и равной его площади:

Составим уравнения моментов относительно опор В и D:

Проведем от опоры В на расстоянии х₁ сечение и составим выражения для Q_x и М_х , для чего найдем величину интенсив­ности нагрузки в сечении х₁ . Из подобия треугольников полу­чим:

Заменим треугольную нагрузку на длине х₁ равнодейству­ющей силой F_x, приложенной в центре тяжести треугольника:

I участок: 0 ≤ х₁ ≤ 2,4 м ;

Из уравнений Q_x и М_х следует, что эпюра Q_x представляет квадратичную параболу, а эпюра М_х — кубическую.

Подставив числовые значения x₁ на границах участка, по­лучим

Так как поперечная сила пересекает ось х, найдем коорди­нату поперечного сечения, в котором Q равна нулю, а изгиба­ющий момент имеет максимальное значение:

По вычисленным данным, в соответствии с правилами построения эпюр, строим эпюры Q и M на первом участке.

II участок: 0 ≤ х₂ ≤ 2,4 м ;

Из эпюр следует, что максимальное значение изгибающий момент имеет в сечении, в котором поперечная сила равна ну­лю, М_max = 14,8 кН*м.

Видео:Эпюры изгибающего момента и поперечной силы от треугольной распределенной нагрузкиСкачать

iSopromat.ru

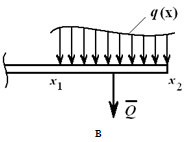
Распределенной нагрузкой называют внешние или внутренние усилия, которые приложены не в одной точке твердого тела (т.е. не сосредоточены в одной точке), а равномерно, случайным образом или по заданному закону распределены по его определенной длине, площади или объему.

Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.

Размерность для линейной нагрузки — Н/м, для нагрузки распределенной по площади — Н/м 2 , для объемной (например при учете собственного веса элементов конструкции) — Н/м 3 .

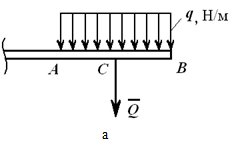
Например, на рисунке 1.23, а приведена равномерно распределенная по длине AB нагрузка интенсивностью q, измеряемая в Н/м. Эта нагрузка может быть заменена сосредоточенной силой

приложенной в середине отрезка AB.

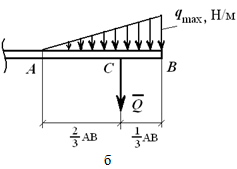
На рисунке 1.23, б показана равномерно убывающая (возрастающая) нагрузка, которая может быть заменена равнодействующей силой

приложенной в точке C, причем AC = 2/3AB.

В произвольном случае, зная функцию q(x) (рисунок 1.23, в), рассчитываем эквивалентную силу

Эта сила приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x).

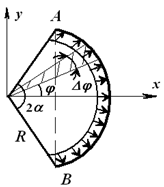
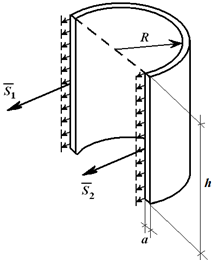
Примером может служить расчет усилий, разрывающих стенки баллона со сжатым газом. Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м]; R – радиус трубы, 2α – центральный угол, ось Ox – ось симметрии (рисунок 1.24).

Выделим элемент сектора с углом ∆φ и определим силу ∆Q, действующую на плоский элемент дуги:

В силу симметрии элемента трубы (с дугой AB) относительно оси Ox проекция результирующей силы на ось Oy:

где АВ – хорда, стягивающая концы дуги.

Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует нагрузка интенсивностью q = p [Н/м, 2 ]. Если цилиндр рассечен по диаметру (рисунок 1.25), то равнодействующая этих сил равна F = q ∙ d ∙ h ( d – внутренний диаметр) или

Разрывающие баллон по диаметру усилия:

Если принять a – толщина стенки, то (пренебрегая усилиями в крышке и дне цилиндра) растягивающее напряжение в стенке равно

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Несимметричная нагрузка. Схема соединения "треугольник"Скачать

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Видео:Преобразование равномерно распределенной нагрузки.Скачать

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Видео:Построение эпюр в балке с треугольной нагрузкой / строительная механикаСкачать

Сосредоточенные силы и распределенные нагрузки

Содержание:

Такие силы называются сосредоточенными. Однако в инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности или линии по тому или иному закону. Распределенные силы прежде всего характеризуются интенсивностью q, т.е. величиной силы, приходящейся на единицу поверхности или линии.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Видео:Максимальный момент от распределенной нагрузки однопролетной балкиСкачать

Сосредоточенные силы и распределенные нагрузки

Мы рассматривали силы, которые были представлены в виде вектора, приложенного к точке. Однако в природе существует большое количество взаимодействий тел, осуществляются не в точке и которые нельзя представить в виде вектора, приложенного к точке.

Такими силовыми факторами являются силы давления жидкости или газа в поверхность твердых тел, силы тяжести, как массовые силы, электромагнитные силы тому подобное. Поэтому в теоретической механике вводится понятие о распределенных силах, которые делятся на поверхностные и объемные.

Поверхностные силы действуют на некоторую поверхность тела. Объемные силы действуют на каждый элемент объема тела, рассматривается. Примером последних сил является сила притяжения.

В теоретической механике рассматривается воздействие на тело только сосредоточенных сил, приложенных к абсолютно твердым телам. А потому
распределенную нагрузку необходимо заменить его равнодействующей, то есть
сосредоточенной силой. Введем несколько общих положений.

Распределенная нагрузка характеризуется его интенсивностью , то есть величиной силы, приходящейся на единицу объема тела (в случае объемных сил), на единицу площади (в случае поверхностных сил) и на единицу длины (если поверхность, на которую действует нагрузка, можно считать линией, то есть шириной поверхности можно пренебречь). В последнем случае распределенная нагрузка называется плоской, на
силовых схемах оно изображается в виде эпюры элементарных сил, то есть графика интенсивности нагрузки, приложенная к линейному элементу тела.

В общем случае распределенная нагрузка изображается в виде определенной кривой, отражающей данный закон изменения интенсивности нагрузки на участке тела (рис. 1.20). Направление действия нагрузки показывается стрелками.

Сначала рассмотрим равномерно распределенную нагрузку и нагрузку, распределенную по линейному закону. Заменяем распределенную нагрузку сосредоточенной силой.

Рассмотрим эти два случая:

— равномерно распределенная нагрузка (или нагрузка, распределенная по закону прямоугольника) изображается на схемах в виде прямоугольника, размеры которого таковы: высота — это интенсивность нагрузки , длина — это длина l участка тела, на которой действует нагрузка. Стрелки показывают направление действия нагрузки (рис. 1.21). Для того, чтобы заменить эту нагрузку равнодействующей силой , надо определить ее. В данном случае

где q — интенсивность нагрузки, Н/м; l — длина участка тела, на которой приложенная нагрузка, м.

Точка C приложения равнодействующей силы размещается посередине участка тела, на которой действует нагрузка. То есть , а направление совпадает с направлением распределенной нагрузки.

— нагрузка распределена по линейному закону (то есть по закону треугольника). В этом случае (рис. 1.22) интенсивность распределенной нагрузки на участке l меняется от 0 до максимального значения q_max. Равнодействующая сила от этой нагрузки по величине равна

Точка C приложения равнодействующей расположена на расстоянии или , а направление совпадает с направлением нагрузки.

Плоская система параллельных сил

Когда линии действия всех сил параллельны, то всегда в плоскости можно так
расположить оси координат, одна из них будет обязательно параллельной заданным силам, а вторая — перпендикулярной. А потому, чтобы тело под действием плоской системы параллельных сил находилось в равновесии, необходимо приравнять к нулю алгебраическую сумму проекций всех сил на параллельную ось и алгебраическую сумму моментов всех сил относительно произвольной точки. В данном случае система условий равновесия (1.54) упрощается и будет иметь такой вид

Для равновесия тела, находящегося под действием системы параллельных сил
на плоскости, необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил
на ось, параллельная силам, и алгебраическая сумма моментов всех сил относительно произвольной точки А плоскости равны нулю.

Для системы параллельных сил на плоскости можно использовать и такие условия равновесия

Для равновесия тела, находящегося под действием системы параллельных сил на плоскости, необходимо и достаточно, чтобы алгебраические суммы моментов всех
сил относительно любых двух точек плоскости равны нулю.

Однако для этих условиях существует ограничение: линия АВ, которой можно соединить
центры моментов, не должна быть параллельной силам.

Данные условия наиболее пригодны при расчетах двухопорных балок. Используя эти условия, составляют алгебраические суммы моментов всех сил относительно точек A и B, в которых установлены опоры балки.

Рассмотрим примеры задач на равновесие тела под действием плоской системы произвольных сил.

Пример:

Однородная балка АВ прямоугольного сечения весом 400 Н имеет один конец А, который закреплен шарнирно, и опирается на точечную опору O (рис. 1.23). Ко второму концу балки В подвешен груз весом 200 Н. Длина балки 4 м, точечная опора расположена на расстоянии ¾ длины балки от шарнирной опоры. Угол наклона балки к горизонту составляет α = 30º.

Определить реакции опор балки.

Краткое условие задачи:

Решение.

Составляем расчетно–силовую схему задачи. Приложим к оси балки заданные активные силы: силу тяжести самой балки и силу притяжения груза. Сила притяжения балки приложена посередине балки в точке C (поскольку балка однородна) и направлена ​​вертикально вниз. Сила притяжения груза приложена к концу балки В и направлена ​​вертикально вниз.

Далее условно освобождаем балку от связей и заменяем их соответствующими реакциями связей. В точке A размещена неподвижная шарнирная опора, она имеет
две составляющие реакции _A и _A, которые расположены вдоль соответствующих осей
координат. В точке O — точечная опора, которая имеет одну реакцию _o, что направлена ​​перпендикулярно к балке.

Таким образом, балка находится в равновесии под действием плоской системы произвольных сил. Для решения этой задачи используем условия равновесия (1.54),

Поскольку оси координат x и y заданные по условию задачи, то составим соответствующие уравнения равновесия

Если подставить значения известных величин в эти уравнения равновесия, то получим

С третьего уравнения вычислим реакцию R_o:

R_o = = 461,86 Н,

и подставим ее значение в первые два уравнения. Будем иметь

Х_А = = R_o = 230,93 Н;

Y_А = 400 + 200 – 0,866 · 461,86 = 160,04 Н.

Поскольку определены две составляющие реакции, приложенные в точке A, — Х_А и Y_А, то геометрическим добавлением можно вычислить модуль полной реакции R_A. А именно:

Таким образом определении все искомые реакции.

Пример.

Определить реакции опоры однородной балки АВ прямоугольного сечения, один конец которого A жестко закреплен в стене и находящийся под действием сосредоточенной силы P = 4,0 kH, пары сил с моментом m = 2,0 kH · м и равномерно распределенной нагрузки интенсивностью q = 1,5 . Длина балки АВ — 5 м, равномерно распределенная
нагрузка действует на участке 3 м от точки A. Угол наклона сосредоточенной силы к горизонту составляет α = 30º, оси x и y показаны на рис. 1.24.

Краткое условие задачи:

q = 1,5 ;

Решение.

Составляем расчетно-силовую схему. Покажем все силы, приложенные к балке АВ. Прежде всего, это заданные активные силы — сила , приложена к концу балки В и направлена под углом α к горизонту. Равномерно распределенную нагрузка заменяем сосредоточенной силой , которая равна

= q · AC =1,5 · 3 = 4,5 kH .

Сила приложена посредине участка AC и направлена ​​в ту же сторону, что и сама нагрузка, то есть вертикально вниз. Покажем на силовой схеме пару сил, которая определяется моментом m.

Далее условно освобождаем балку от вязи и заменяем ее соответствующими реакциями вязи. В точке A — жесткое закрепление балки в стене, а потому оно имеет две составляющие реакции: _A, _A, которые расположены вдоль соответствующих осей
координат, и реактивный момент M_A. Направление этого неизвестного момента
показываем на силовой схеме произвольно, например, — против направления стрелки
часов. Если же при окончательном определении момента M_A получим отрицательный знак, то получим, что действительное направление момента — противоположно. Покажем на силовой схеме линейные и угловые размеры. Оси координат показаны на схеме.

Как видно из построенной расчетно–силовой схемы, балка находится под действием плоской системы произвольных сил. Используем условия равновесия (1.54). А именно = 0.

Составим соответствующие уравнения равновесия

Если подставить значения известных величин в эти уравнения равновесия, то получаем

Из первого уравнения вычислим X_A:

X_A = 4,0 = = 3,46 kH.

Из второго уравнения вычислим Y_A:

Y_A = 4,5 + 4,0 · = 6,50 kH.

С третьего уравнения вычислим M_A:

M_A = 2,0 + 4,5 + 4,0 · 5 = 2,0 + 6,75 + 10,0 = 18,75 kH.

Поскольку составляющие реакций X_A и Y_A, приложенных в точке A, вычислены, то можно найти модуль R_A полной реакции в точке A. Будем иметь

Таким образом, определены все искомые реакции.

Равновесие системы тел

Системой тел называется совокупность нескольких тел, или которые опираются друг на друга, или соединены шарнирами, которые дают возможность относительного движения тел.

При решении задач на систему тел различают силы внешние и внутренние.

Внешние силы — это силы взаимодействия тел данной системы с другими телами, которые не входят в состав системы.

Внутренние силы — это силы взаимодействия между отдельными телами, которые входят в состав данной системы. Внутренние силы существуют попарно, как действие и
противодействие.

Статически обозначенные и статически неопределенные задачи

Задача является статически обозначенной, если для нее можно составить такое
количество уравнений равновесия материальной системы, не меньше, чем число
неизвестных.

Задача, является статически неопределенной, если число уравнений равновесия
системы меньше, чем число неизвестных.

В теоретической механике рассматриваются только статически обозначенные
материальные системы.

Методика решения задач на равновесие системы тел

Равновесие системы тел можно рассматривать в целом под действием только
внешних сил. Но может так случиться, что количество уравнений равновесия будет
меньше, чем количество неизвестных. Тогда необходимо рассматривать равновесие
отдельных тел системы, условно разделяя ее обязательно по внутренним связям. Причем необходимо учитывать, что внутренние силы реакций входят попарно, как действие и противодействие.

Рассмотрим пример решения задач на равновесие системы тел.

Пример.

На трех-шарнирную арку А В С (рис. 1.25) действует вертикальная сила Р = 10 kH. Вес каждой части балки Q₁ = Q₂ = 6 kH. Определить реакции шарниров А, В, С арки, размеры которой данные на рисунке.

Решение.

Как видно из схемы, заданная система тел состоит из двух пиварок I и II, которые соединены шарниром в точке С. Составим расчетно–силовую схему, где покажем заданные активные силы Q₁, Q₂, и реакции связей: в точках A и B (неподвижные шарнирные опоры) — _{A ,A} и _{В , В} и в точке C (шарнирное соединение) — _C , ´_C и _{C ,} ´_С. Эти неизвестные реакции в точке С являются внутренними силами системы тел, а потому _C = ´_C и _C = ´_С.

Покажем оси прямоугольной декартовой системы координат Axy.

Условно разделяем систему тел на два отдельных тела по шарниру С. Действие отброшенной части заменяем двумя реакциями _C и _C, которые равны

Теперь рассмотрим отдельно равновесие каждого тела, для чего составим две системы уравнений равновесия. Используем условия равновесия.

Для первого тела (левая половина арки):

= 0; Х_А — Х_С = 0,

= 0; Y_A + Y_C — Q₁ — P = 0,

= 0; Х_С · 4 + Y_C · 5 — Q₁ · 1 — P · 4 = 0.

Для второго тела (правая половина арки):

= 0; Х_B — Х´_С = 0,

= 0; Y_B + Y´_C — Q₂ — P = 0,

= 0; Q₂ · 1 — Х´_{С ·} 4 + Y´_C · 5 = 0.

Определим эти неизвестные величины. С третьего уравнения второй системы определим Y´_{C .} Перепишем это уравнение следующим образом:

Поскольку численно Y´_C = Y_C , а Х_С = Х´_С, то подставив значения этих реакций в третье уравнение первой системы, получаем

Теперь есть возможность определить неизвестную реакцию Y´_C . Подставив значение X_C в третье уравнение второй системы, будем иметь

Из первого уравнения первой системы имеем X_A = X_C = 6,5 kH. А с первого уравнения второй системы должны X_B = – X´_C = – 6,5 kH. Направление этой реакции противоположно показанному на силовой схеме. Из второго уравнения первой системы получаем

Из второго уравнения второй системы вычислим последнюю неизвестную реакцию Y_B. Она будет равняться Y_B = Y´_C + Q₂ = 4,0 + 6,0 = 10,0 kH.

Таким образом вычислено все искомые величины.

Ответ:

Услуги по теоретической механике:

Учебные лекции:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

🎥 Видео

Нагрузка, распределенная по дугеСкачать

Определение опорных реакций балки. Сопромат для чайников ;)Скачать

БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!Скачать

Консольный стержень, загруженный равномерно распределенной нагрузкой. ПРАВИЛЬНЫЙ СОПРОМАТ. Видео 4.Скачать

Определение усилий, напряжений и перемещений. СопроматСкачать

Определение реакций опор в балке. Сопромат.Скачать

Распределённая нагрузка описанная функцией, определение результирующей силы с помощью интеграла.Скачать

Урок 1.6: Активная и реактивные нагрузкиСкачать

Составная рама с линейно распределенной нагрузкойСкачать

Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Классификация сил. Волшебное преобразование нагрузок. Сопромат-Тайные Знания 3.Скачать

Статический расчет балки с распределенной нагрузкой аналитическим методомСкачать

Определение усилий в сечениях арки с треугольной нагрузкойСкачать