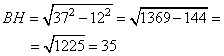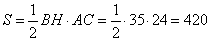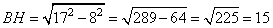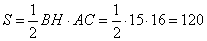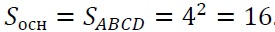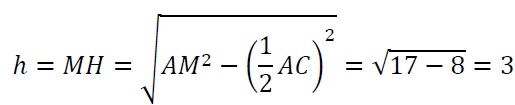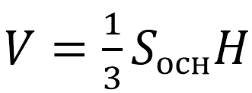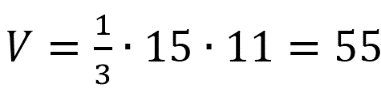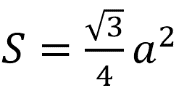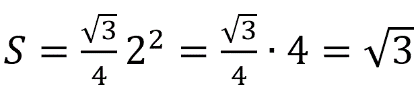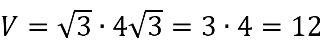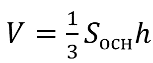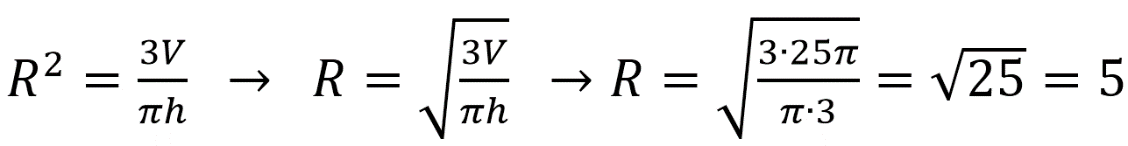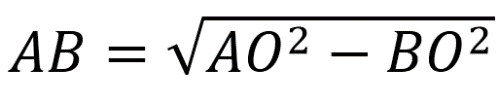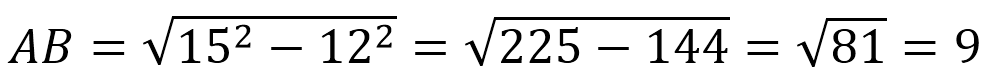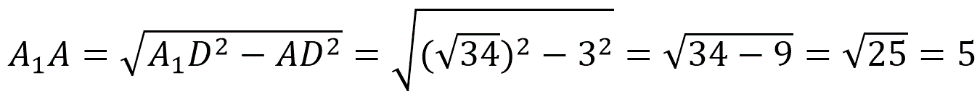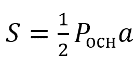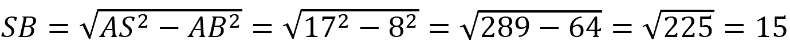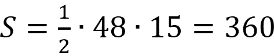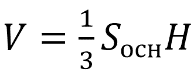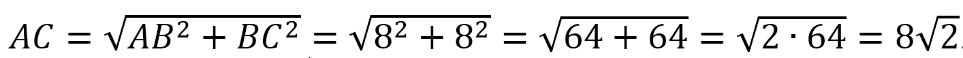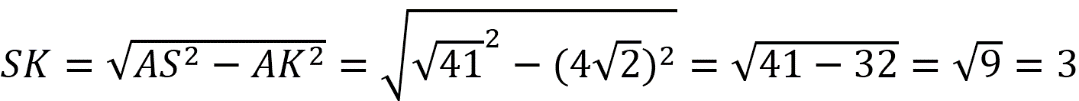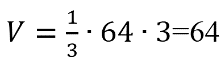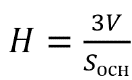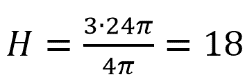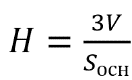Основанием наклонной четырехугольной призмы авсда1в1с1д1 является четырехугольник авсд в котором 6 4

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Ваш ответ

Видео:№341. Основанием четырехугольной пирамиды с вершиной Р является трапеция ABCDСкачать

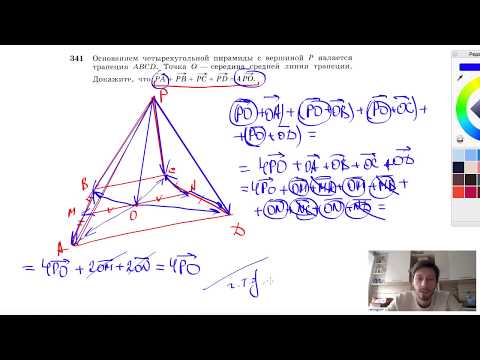
решение вопроса

Видео:№225. Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол в 30°.Скачать

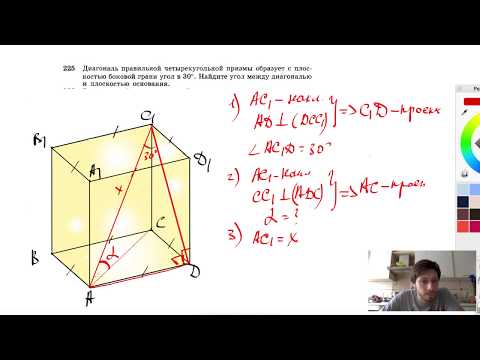
Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,739
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:№224. Диагональ правильной четырехугольной призмы наклонена к плоскости основания под углом 60°Скачать

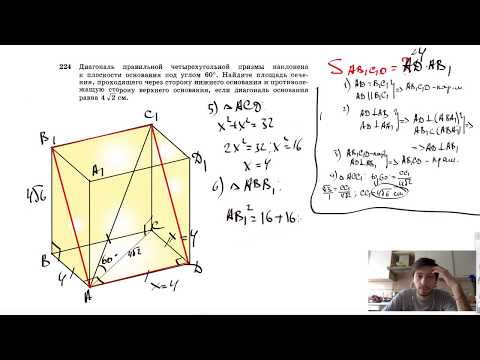
Задание №16 ЕГЭ по математике базового уровня

Видео:№226. В правильной четырехугольной призме через диагональ основания проведено сечениеСкачать

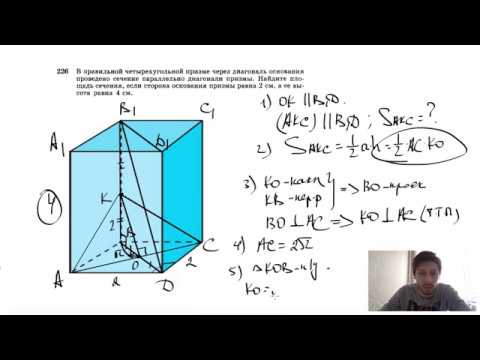
Стереометрия

В задании №16 базового уровня ЕГЭ по математике нам предстоит столкнуться со стереометрией. Как таковой «стереометрии» мы не встретим, обычно условие задания содержит объемную фигуру, в которой нам необходимо найти какое-либо расстояние. В данном задании необходимо правильно применить пространственное мышление и выбрать нужное сечение, остальные расчеты происходят в плоскости, причем по несложным формулам (теорема Пифагора и т.д.). Какой-либо конкретной теории я пока приводить не буду, а рассмотрю типовые варианты, на которых мы и рассмотрим алгоритмы решения задач данного типа.

Разбор типовых вариантов заданий №16 ЕГЭ по математике базового уровня

Вариант 16МБ1

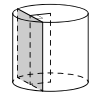
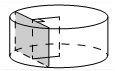
Радиус основания цилиндра равен 13, а его образующая 18. Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12. Найдите площадь этого сечения.

Алгоритм выполнения:

1. Определить тип фигуры, образующей сечение.
2. Записать формулу для нахождения площади фигуры, образующей сечение.
3. Вычислить недостающие данные.
4. Вычислить искомую площадь сечения.

Решение:

Из рисунка видно, что сечение является прямоугольником, одна из сторон которого образующая цилиндра.

Площадь прямоугольника равна произведению длины на ширину.

Длина прямоугольника – 18, из условия. Осталось вычислить ширину. Сделаем дополнительный чертеж цилиндра сверху:

Ширина прямоугольника – CD.

По условию «Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12». Расстояние от точки до прямой – это длина перпендикуляра, проведенного из этой точки на прямую. То есть на чертеже АВ = 12.

СD = СВ + ВD. СВ = ВD

Рассмотрим треугольник ВСА. Треугольник ВСА – прямоугольный.

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

В данном случае СА 2 = СВ 2 + АВ 2

СВ 2 — неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.

СВ 2 = СА 2 — АВ 2

СВ = √(13 2 — 12 2 ) = √(169 — 144) = √25 = 5

Для решения задачи необходимо знать СD = СВ + ВD = 5 + 5 = 10

Вычислим искомую площадь сечения.

Вариант 16МБ2

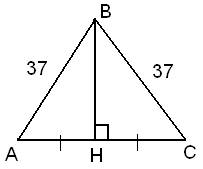
Стороны основания правильной треугольной пирамиды равны 24, а боковые рёбра равны 37. Найдите площадь боковой поверхности этой пирамиды.

Алгоритм выполнения:

1. Проанализировать какие данные необходимо вычислить для ответа на вопрос задачи.
2. Найти площади треугольников.
3. Найти площадь боковой поверхности пирамиды.

Решение:

Проанализируем, какие данные необходимо вычислить для ответа на вопрос задачи.

В основании правильной треугольной пирамиды лежит равносторонний треугольник. Боковые ребра пирамиды, равные 37, образуют три равнобедренных треугольника, которые составляют ее боковую поверхность.

Найдем площади треугольников.

Так как треугольник равнобедренный, то высота BH делит сторону AC пополам, то есть, AH=AC:2=24:2=12. Рассмотрим треугольник АВН. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. В данном случае АВ 2 = ВН 2 + АН 2

ВН 2 — неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.

ВН 2 = АВ 2 — АН 2 Следовательно, высота BH, равна:

Площадь треугольника равна половине произведения основания на высоту.

Тогда, площадь треугольника может быть вычислена как

Найдем площадь боковой поверхности пирамиды.

Боковая поверхность пирамиды состоит из трех треугольников. Найдем ее площадь:

Ответ: 1260.

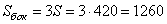
Вариант 16МБ3

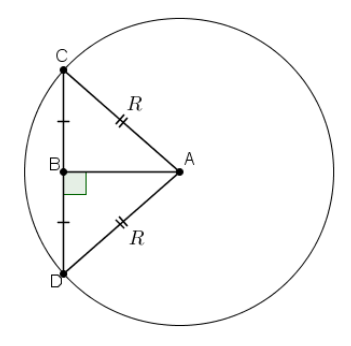
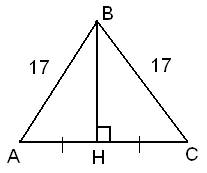
Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.

Алгоритм выполнения:

1. Проанализировать какие данные необходимо вычислить для ответа на вопрос задачи.
2. Найти площади треугольников.
3. Найти площадь боковой поверхности пирамиды.

Решение:

Проанализируем, какие данные необходимо вычислить для ответа на вопрос задачи.

В основании правильной треугольной пирамиды лежит равносторонний треугольник. Боковые ребра пирамиды, равные 17, образуют три равнобедренных треугольника, которые составляют ее боковую поверхность.

Найдем площади треугольников.

Так как треугольник равнобедренный, то высота BH делит сторону AC пополам, то есть, AH=AC:2=16:2=8.

Рассмотрим треугольник АВН.

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

В данном случае АВ 2 = ВН 2 + АН 2

ВН 2 — неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.

ВН 2 = АВ 2 — АН 2

Следовательно, высота BH, равна:

Площадь треугольника равна половине произведения основания на высоту.

Тогда, площадь треугольника может быть вычислена как

Найдем площадь боковой поверхности пирамиды.

Боковая поверхность пирамиды состоит из трех треугольников. Найдем ее площадь:

Ответ: 360.

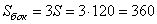
Вариант 16МБ4

Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно √17.

Вспомним формулу площади правильной пирамиды — одна треть от произведения площади основания и высоты.

Площадь основания рассчитываем по формуле площади квадрата — квадрат стороны:

После этого перейдем к нахождению высоты. Для этого нам необходимо рассмотреть прямоугольный (так как основание перпендикулярно высоте) треугольник AMH. AH — половина диагонали квадрата, которая равна √2 его стороны, то есть в нашем случае диагональ равна 4√2, ну а половина — AH = 2√2. Зная гипотенузу и один из катетов, найдем высоту:

После этого легко вычисляем объем:

V = 1/3 • 16 •3 = 16

Вариант 16МБ5

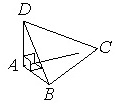
В треугольной пирамиде АВСD ребра АВ, АС и АD взаимно перпендикулярны. Найдите объем этой пирамиды, если АВ=2, АС=15 и AD=11.

Алгоритм выполнения

1. Записываем формулу для определения объема пирамиды.
2. Находим площадь основания по формуле для площади прямоугольного треугольника.
3. Показываем, что высота пирамиды совпадает с ребром AD. Вычисляем искомый объем.

Решение:

Т.к. в основании пирамиды лежит прямоугольный треугольник с катетами АВ и АС (по условию АВ перпендикулярно АС), то S_осн=АВ·АС/2.

Т.к. AD перпендикулярно АВ и АС и пересекается с ними в одной точке, то (по признаку перпендикулярности прямой и плоскости) AD перпендикулярно плоскости основания пирамиды.

Значит AD – высота пирамиды. Т.е. Н=AD=11.

Вариант 16МБ6

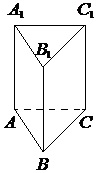
Сторона основания правильной треугольной призмы АВСА₁В₁С₁ равна 2, а высота этой призмы равна 4√3. Найдите объем призмы АВСА₁В₁С₁.

Алгоритм выполнения

1. Находим площадь основы призмы через формулу для площади правильного треугольника.
2. Записываем формулу для объема призмы. Подставляем в нее числовые данные, вычисляем искомую величину.

Решение:

Площадь правильного треугольника равна:

Здесь а – сторона основания призмы.

Объем призмы: V=Sh, где h – высота призмы, S– площадь ее основания (в нашем случае – площадь правильного треугольника, лежащего в основании).

Вариант 16МБ7

Объем конуса равен 25π, а его высота равна 3. Найдите радиус основания конуса.

Алгоритм выполнения

1. Записываем формулу для объема конуса. Из нее выражаем площадь основания.
2. Площадь основания расписываем по формуле площади круга, поскольку именно круг лежит в основании конуса.
3. Из этих двух формул выражаем искомую величину. Вычисляем ее.

Решение:

Объем конуса равен:

Площадь круга составляет:

Вариант 16МБ8

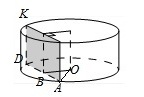
Радиус основания цилиндра равен 15, а его образующая равна 14. Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12. Найдите площадь этого сечения.

Алгоритм выполнения

1. Определяем, что образующая цилиндра – это одна из сторон сечения-прямоугольника. Вводим обозначения для точек, которые необходимы для выполнения расчетов. Получаем, что образующая – это отрезок DK.
2. Делаем дополнительное построение – соединяем точки О и А в основании цилиндра. Получаем прямоугольный ∆АВО.
3. Из ∆АВО по т.Пифагора находим значение АВ. Этот отрезок – половина AD. Отсюда находим AD.
4. Зная величину DK и AD, вычисляем площадь сечения-прямоугольника.

Решение:

Поскольку образующая цилиндра и его высота совпадают, то DK=14. Это – одна из сторон прямоугольника, форму которого и имеет сечение.

Найдем 2-ю сторону этого прямоугольника. Из прямоугольного ∆АВО по т.Пифагора АО 2 =АВ 2 +ВО 2 .

АО – радиус основания, поэтому АО=15. ВО=12, поскольку ВО – это расстояние от оси до плоскости сечения.

Площадь сечения равна:

Вариант 16МБ9

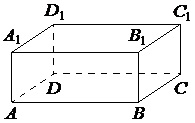
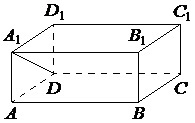
В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ ребра DA, DC и диагональ DA₁ боковой грани равны соответственно 3, 5 и √34. Найдите объем параллелепипеда ABCDA₁B₁C₁D₁.

Алгоритм выполнения

1. Соединяем вершины А₁ и D. Получаем прямоугольный ∆А₁АD. Из этого треугольника находим АА₁.
2. Записываем формулу для вычисления объема параллелепипеда. Находим значение для объема.

Решение:

Т.к. ABCDA₁B₁C₁D₁ параллелепипед, то угол А₁АD равен 90 0 . Поэтому ∆А₁АD – прямоугольный. Тогда по т.Пифагора А₁А 2 +AD 2 =A₁D 2 . Отсюда получаем:

Объем параллелепипеда найдем по формуле:

Вариант 16МБ10

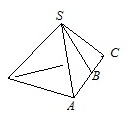
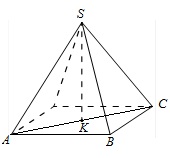
Стороны основания правильной треугольной пирамиды равны 16, а боковые ребра равны 17. Найдите площадь боковой поверхности этой пирамиды.

Алгоритм выполнения

1. Записываем формулу для площади боковой поверхности через периметр основания и апофему.
2. Находим периметр треугольника, лежащего в основании пирамиды.
3. Доказываем, что апофема является не только высотой, но и медианой для боковой стороны пирамиды.
4. Из прямоугольного треугольника, образованного апофемой, боковым ребром и половиной стороны основания, по т.Пифагора находим величину апофемы.
5. Вычисляем площадь боковой поверхности пирамиды.

Решение:

Площадь боковой поверхности пирамиды равна:

Находим периметр основания:

Т.к. пирамида правильная, то ее боковые грани – равнобедренные треугольники. Тогда апофема, которая является высотой боковой грани, проведенной к основанию, является еще и медианой. Значит, SB – медиана и АВ=АС/2=16/2=8.

Из прямоугольного ∆ABS по т.Пифагора АВ 2 +SB 2 =AS 2 .

Вариант 16МБ11

Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 8, а боковое ребро равно √41.

Алгоритм выполнения

1. Записываем формулу для объема пирамиды через площадь ее основания и высоту.
2. Находим площадь основания, учитывая, что в основании пирамиды лежит квадрат.
3. Находим диагональ квадрата, лежащего в основании, как гипотенузу из ∆АВС. Используем для этого т.Пифагора Делим полученную величину пополам.
4. Из треугольника, построенного на половине диагонали основания, высоте пирамиды и ее боковом ребре, по т.Пифагора определяем высоту.
5. Вычисляем объем.

Решение:

Т.к. пирамида правильная, то четырехугольник в ее основании – это квадрат. Поэтому S_осн=а 2 , где а – сторона основания.

Из прямоугольного ∆АВС по т.Пифагора АС 2 =АВ 2 +ВС 2 .

Из прямоугольного ∆АКS по т.Пифагора AS 2 =AK 2 +SK 2 .

Значит, объем пирамиды составляет:

Вариант 16МБ12

Два ребра прямоугольного параллелепипеда равны 8 и 5, а объем параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.

Алгоритм выполнения

1. Записываем формулу для объема прямоугольного параллелепипеда. Из нее выражаем 3-е (неизвестное) ребро. Вычисляем величину этого ребра.
2. Записываем формулу для площади поверхности. Подставляем в него числовые данные, находим искомое значение.

Решение:

Объем прямоугольного параллелепипеда равен:

V=abc, где a, b, c – ребра. Будем считать, что a и b нам известны, а с – неизвестно.

Тогда из этой формулы:

Площадь поверхности прямоугольного параллелепипеда вычисляется так:

Вариант 16МБ13

Объем конуса равен 24π, а радиус его основания равен 2. Найдите высоту конуса.

Алгоритм выполнения

1. Записываем формулу для объема конуса. Из нее выражаем высоту.
2. Записываем формулу для площади круга, лежащего в основе конуса. Вычисляем эту площадь.
3. Подставляем числовые данные в формулу для объема, вычисляем искомую величину.

Решение:

Объем конуса составляет:

.

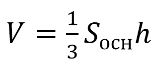
Площадь основания (как площадь круга) равна:

Тогда высота конуса:

Вариант 16МБ14

Основанием четырехугольной пирамиды является прямоугольник со сторонами 3 и 12. Найдите высоту этой пирамиды, если ее объем равен 60.

Алгоритм выполнения

1. Записываем формулу для объема пирамиды через площадь ее основания и высоту. Из нее выражаем высоту.
2. Находим площадь основы-прямоугольника.
3. Подставляем числовые данные в формулу для высоты, вычисляем искомую величину.

Решение:

Объем пирамиды вычисляется так:

Отсюда:

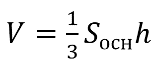
S_осн=ab, a и b – стороны прямоугольника, лежащего в основе пирамиды.

Видео:Площадь поверхности призмы. 11 класс.Скачать

Вариант 1

Вариант 1.

А1. A1 D

Какие из следующих пар прямых являются B1 C1 скрещивающимися? A

Укажите плоскость, параллельную прямой, D C

проходящей через точки пересечения B

диагоналей граней AA1B1B и BB1C1C A

Основание призмы – правильный треугольник со A1 B1

стороной 6, а её боковое ребро равно 8 и

наклонено к плоскости основания под углом 600. C1

Найдите объём призмы.

1)

A B

А4. B1 C1

Высота правильной четырёхугольной призмы

ABCDA1B1C1D1 равна 4, а сторона основания A1

– 4. Найдите расстояние между вершиной C и

точкой пересечения диагоналей боковой

грани AA1B1B C

1) 2 2) 4 3) 4 4) 2

Основание прямой призмы – прямоугольник со сторонами 4 и 3, а её высота равна 3. Найдите тангенс угла между диагональю призмы и плоскостью большей по площади боковой грани.

1) 2) 3) 4)

Высота правильной шестиугольной призмы равна 3, а площадь основания — . Найдите длину большей диагонали призмы.

Высота правильной четырёхугольной призмы ABCDA1B1C1D1 равна , а сторона основания — . На продолжении бокового ребра BB1 за точку B1 отложен отрезок B1K, равный ребру BB1. Найдите площадь сечения, проходящего через точки A,C и K.

Сторона основания правильной четырёхугольной призмы ABCDA1B1C1D1 равна 8, а боковое ребро – 6. Точка К – середина отрезка ВС, точка О – середина отрезка СD1. Найдите объём многогранника AA1KO.

В правильной четырёхугольной призме боковое ребро равно стороне основания. Найдите угол между диагональю призмы и скрещивающейся с ней диагональю боковой грани.

А1. A B

Какие из следующих пар прямых являются D C

Укажите плоскость, параллельную прямой, B C

проходящей через точки пересечения

диагоналей граней AA1D1D и AA1B1B A D

1) B1C1D1 2) BDA1 3) BDD1 4) B1CC1 B1 C1

A1 D1

Основание призмы – правильный треугольник с A1 B1

высотой, равной , а её боковое ребро равно и

наклонено к плоскости основания под углом 600. C1

Найдите объём призмы.

1) 2)

A B

А4. B1 C1

Высота правильной четырёхугольной призмы

ABCDA1B1C1D1 равна , а сторона основания A1

– 2. Найдите расстояние между вершиной C и

точкой пересечения диагоналей боковой

грани AA1B1B C

1) 2,5 4)

Основание прямой призмы – прямоугольник со сторонами 4 и 3, а её высота равна 3. Найдите тангенс угла между диагональю призмы и плоскостью меньшей по площади боковой грани.

1) 2) 3) 4)

Высота правильной шестиугольной призмы равна 2, а площадь основания — . Найдите меньшую диагональ призмы.

Высота правильной четырёхугольной призмы ABCDA1B1C1D1 равна , а сторона основания — 8. На продолжении ребра АА1 за точку А1 отложен отрезок А1М, равный высоте призмы. Найдите площадь сечения, проходящего через точки B,D и M.

Сторона основания правильной четырёхугольной призмы ABCDA1B1C1D1 равна 16, а боковое ребро – 12. Точка М – середина стороны основания АD, точка Р – середина отрезка АВ1. Найдите объём многогранника СС1РМ.

В правильной четырёхугольной призме боковое ребро равно стороне основания. Найдите угол между диагональю призмы и скрещивающейся с ней диагональю боковой грани.

А1. A B

Какие из следующих пар прямых являются D C

1) A1D1 и B1C1 2) BC1 и AD13) AD1 и A1D 4) AB1 и A1D1

Укажите плоскость, параллельную прямой, B C

проходящей через точки пересечения

диагоналей граней AA1D1D и B1BCC1 A D

1) B1C1D 2) BDA1 3) AA1B 4) B1CC1 B1 C1

A1 D1

Основание призмы – правильный треугольник. А1 В1

Радиус окружности, описанной около основания равен , С1

а её боковое ребро равно и наклонено к плоскости

основания под углом 600.

Найдите объём призмы. А В

1) К

А4. B1 C1

Основание прямой четырёхугольной призмы

ABCDA1B1C1D1 — прямоугольник со сторонами А1

АВ=6 и ВС=12. Высота призмы равна 8.

Найдите расстояние между вершиной С и точкой

пересечения диагоналей грани AA1B1B .

1) 6,5 4)

Основание прямой четырёхугольной призмы – прямоугольник со сторонами 8 и 6, а её высота равна 6. Найдите синус угла между диагональю призмы и плоскостью большей по площади боковой грани.

1) 2) 3) 4)

Высота правильной шестиугольной призмы равна 3, а радиус окружности, вписанной в основание, . Найдите длину большей диагонали призмы.

Высота правильной четырёхугольной призмы ABCDA1B1C1D1 равна , а сторона основания — 6. На продолжении ребра BB1 за точку B1 отложен отрезок B1К, равный половине ребра BB1. Найдите площадь сечения, проходящего через точки А, С и К.

В основании прямоугольного параллелепипеда MNPQM1N1P1Q1 лежит квадрат со стороной 8, боковое ребро равно 6. Точка К – середина отрезка M1N1, точка О – середина отрезка N1P. Найдите объём многогранника QQ1КО.

В правильной четырёхугольной призме боковое ребро равно стороне основания. Найдите угол между диагональю призмы и скрещивающейся с ней диагональю боковой грани.

А1. A B

Какие из следующих пар прямых являются D C

Укажите плоскость, параллельную прямой, B C

проходящей через точки пересечения

диагоналей граней ABCD и AA1B1B A D

1) B1C1D 2) B1CC1 3) BDD1 4) BDA1 B1

A1 D1

В основании наклонной призмы лежит правильный А1 В1

треугольник. Радиус окружности, вписанной в основание, С1

равен , а её боковое ребро, равное 4, наклонено к

плоскости род углом 600. Найдите объём призмы.

1) 54 2) 18

А В

А4. B1 C1

В основании прямой четырёхугольной призмы

ABCDA1B1C1D1 лежит прямоугольник со А1

сторонами АВ=6 и ВС=12. Высота призмы — 8.

Найдите расстояние между вершиной А и точкой

пересечения диагоналей грани B1BСС1. С

1) 4)

В основании прямой четырёхугольной призмы лежит прямоугольник со сторонами 4 и 3, а её высота равна 3. Найдите синус угла между диагональю призмы и плоскостью меньшей по площади боковой грани.

1) 2) 3) 4)

Высота правильной шестиугольной призмы равна 2, а радиус окружности, вписанной в основание, . Найдите меньшую диагональ призмы.

Высота правильной четырёхугольной призмы ABCDA1B1C1D1 равна , а сторона основания — 12. На продолжении ребра АА1 за точку А1 отложен отрезок А1М, равный половине высоте призмы. Найдите площадь сечения, проходящего через точки B,D и M.

Сторона основания правильной четырёхугольной призмы EFGHE1F1G1H1 – квадрат со стороной 16, а боковое ребро равно 12. Точка М – середина отрезка E1H1, точка Р – середина отрезка GH1. Найдите объём многогранника FF1РМ.

В правильной четырёхугольной призме боковое ребро равно стороне основания. Найдите угол между диагональю призмы и скрещивающейся с ней диагональю боковой грани.

А1. A B

Какие из следующих пар прямых являются D C

Укажите плоскость, параллельную прямой, B C

проходящей через точки пересечения

диагоналей граней СС1D1D и AA1B1B A D

1) B1C1D 2) BDA1 3) BDD1 4) B1CС1 B1

A1 D1

Основание наклонной призмы – ромб с

меньшей диагональю 4 и углом 600, а её боковое D1 C1

ребро, равное , наклонено к плоскости

основания под углом 600. A B

Найдите объём призмы.

1) 2)K

А4. B1 C1

Высота правильной четырёхугольной призмы

ABCDA1B1C1D1 равна 8, а сторона основания A1

– 8. Найдите расстояние между вершиной A и

точкой пересечения диагоналей

грани DD1C1C. C

1) 4 2) 8 3) 8 4) 4

В основании прямой четырёхугольной призмы лежит прямоугольник со сторонами 12 и 9, а её высота равна 9. Найдите котангенс угла между диагональю призмы и плоскостью большей по площади боковой грани.

1) 2) 3) 4)

Большая диагональ правильной шестиугольной призмы равна 5, а площадь основания — . Найдите высоту призмы.

Высота правильной четырёхугольной призмы ABCDA1B1C1D1 равна , а сторона основания — . На продолжении бокового ребра BB1 за точку B1 отложен отрезок B1K так, что отношение BK : B1K=2:1. Найдите площадь сечения, проходящего через точки A,C и K.

Сторона основания правильной четырёхугольной призмы ABCDA1B1C1D1 равна 4, а боковое ребро – 3. Точка К – середина отрезка АD, точка О – середина отрезка СD1. Найдите объём многогранника ВВ1KO.

В правильной четырёхугольной призме боковое ребро равно стороне основания. Найдите угол между диагональю призмы и скрещивающейся с ней диагональю боковой грани.

Какие из следующих пар прямых являются В

скрещивающимися? С1

1) А1В1 и СВ 2) DС и D1С1 D

Укажите плоскость, параллельную прямой, B C

проходящей через точки пересечения

диагоналей граней СС1D1D и A1B1С1D1 A D

1) B1C1D 2) B1CС1 3) BDD1 4) BDA1 B1 С1

A1 D1

Основание призмы – ромб с меньшей диагональю

4 и углом 1200, её боковое ребро наклонено к D1 C1

плоскости основания под углом 600 и равно

. Найдите объём призмы. А

1) 2)

А4. B1 C1

Высота правильной четырёхугольной призмы

ABCDA1B1C1D1 равна , а сторона основания A1

– 2. Найдите расстояние между вершиной A и

точкой пересечения диагоналей

грани DD1C1C. C

1) 2,5 4)

Основание прямой призмы — прямоугольник со сторонами 4 и 3, а её высота равна 3. Найдите котангенс угла между диагональю призмы и плоскостью большей по площади боковой грани.

1) 2) 3) 4)

Длина меньшей диагонали правильной шестиугольной призмы равна 4, а площадь основания — . Найдите высоту призмы.

Высота правильной четырёхугольной призмы ABCDA1B1C1D1 равна , а сторона основания — 8. На продолжении ребра АА1 за точку А1 отложен отрезок А1М так, что отношение высоты призмы к отрезку АМ равно 1:2. Найдите площадь сечения, проходящего через точки B,D и M.

Сторона основания правильной четырёхугольной призмы ABCDA1B1C1D1 равна 4, а боковое ребро – 3. Точка М – середина стороны основания СD,

точка Р – середина отрезка А1D . Найдите объём многогранника ВВ1РМ.

В правильной четырёхугольной призме боковое ребро равно стороне основания. Найдите угол между диагональю призмы и скрещивающейся с ней диагональю боковой грани.

Какие из следующих пар прямых являются В

скрещивающимися? С1

1) MQ и P1N1 2) QP и MN D

Укажите плоскость, параллельную прямой, B C

проходящей через точки пересечения

диагоналей граней D1D СС1 и ABСD A D

1) B1CС1 2) BDA1 3) B1C1D 4) BDD1 B1 С1

A1 D1

Основание призмы – ромб с большей диагональю

и углом 1200, а её боковое ребро равно D1

и наклонено к плоскости основания C1

Найдите объём призмы.

1) 2) К

D C

А4. B1 C1

В основании прямой четырёхугольной призмы

ABCDA1B1C1D1 — прямоугольник с основаниями А1

АВ=12 и ВС=24. Высота призмы равна 16.

Найдите расстояние между вершиной А и точкой

пересечения диагоналей грани DD1С1С. С

1) 4)

В основании прямой четырёхугольной призмы лежит прямоугольник со сторонами 4 и 3, а её высота равна 3. Найдите косинус угла между диагональю призмы и плоскостью большей по площади боковой грани.

1) 2) 3) 4)

Площадь основания правильной шестиугольной призмы равна . Найдите длину большей диагонали призмы, если она составляет с плоскостью основания угол 450.

Высота правильной четырёхугольной призмы ABCDA1B1C1D1 равна , а сторона основания -6. На продолжении бокового ребра BB1 за точку B1 отложен отрезок B1Т так, что отношение B1Т : ВB1 равно 1 : 2. Найдите площадь сечения, проходящего через точки A,C и Т.

Боковое ребро прямого параллелепипеда MNPQM1N1P1Q1 равно 9, основание — квадрат со стороной 12. Точка К – середина отрезка M1N1, точка О – середина отрезка N1P. Найдите объём многогранника QQ1КО.

В правильной четырёхугольной призме боковое ребро равно стороне основания. Найдите угол между диагональю призмы и скрещивающейся с ней диагональю боковой грани.

💥 Видео

Задача о вычислении диагонали четырёхугольной призмыСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

№292. В правильной четырехугольной призме сторона основания равна 6 см, боковое ребро равно 8Скачать

№233. Основанием прямой призмы АВСA1B1C1 является прямоугольный треугольник ABCСкачать

10 класс, 30 урок, ПризмаСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

№259. В правильной четырехугольной пирамиде сторона основания равна 6 см, а угол наклона боковойСкачать

Пространственные фигуры. Прямые и плоскости. Математика 10 класс. Вебинар | TutorOnlineСкачать

Как строить сечения параллелепипедаСкачать

Стереометрия, номер 10.1Скачать

Занятие 1. Пространственные фигуры. Прямые и плоскости. Математика 10 классСкачать

Призма и пирамида. Площадь и объем. Вебинар | Математика 10 классСкачать

Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основанияСкачать