Прототипы заданий 15 ОГЭ по математике. Материал для подготовки к ОГЭ.
Для выполнения задания 15 необходимо уметь выполнять действия с геометрическими фигурами, координатами и векторами (т реугольники, четырёхугольники, многоугольники и их элементы)
Подробнее узнать виды заданий на данной позиции в КИМах можно по кодификатору
| Карточки для отработки задания 15 с ответами → скачать |
| Прототипы задания 15 ОГЭ по математике (треугольники) Опубликовано: Гармс Людмила Павловна → скачать |
| Материалы для отработки задания 15 Автор: Е. А. Ширяева Решение типовых задач № 15 на ОГЭ по математике 111 Содержание Видео:Задание №16 ОГЭ. Треугольники, четырёхугольники, многоугольники и их элементы.Скачать  Четырехугольники и многоугольникиВидео:Задание 15 ОГЭ 2023 математика | Треугольники, четырёхугольники и их элементыСкачать  Четырехугольники и многоугольники.Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Свойства параллелограмма:1. В параллелограмме противоположные стороны и углы попарно равны. 2. Диагональ делит параллелограмм на два равных треугольника. 3. Диагонали точкой пересечения делятся пополам. 4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. 5. Биссектриса угла в параллелограмме отсекает от него равнобедренный треугольник. 6. В параллелограмме биссектрисы углов, прилежащих к одной стороне (соседних углов), пересекаются под углом в $90°$.
Прямоугольник — это параллелограмм, у которого все углы прямые.
Площадь прямоугольника равна половине произведения смежных (соседних) сторон. $S=a·b$, где $а$ и $b$ — смежные стороны. Ромб — это параллелограмм, у которого все стороны равны.
1. Площадь ромба равна половине произведения его диагоналей. $S=/$, где $d_1$ и $d_2$ — диагонали ромба 2. Площадь ромба равна произведению квадрата стороны на синус острого угла ромба. $S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами. Квадрат – это прямоугольник, у которого все стороны равны.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие нет. Параллельные стороны называются основаниями: $ВС$ и $AD$ — основания. Непараллельные стороны называются боковыми сторонами: $АВ$ и $CD$ – боковые стороны. Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции. Свойства средней линии трапеции: 1. Средняя линия параллельна основаниям трапеции. 2. Средняя линия равна полусумме оснований. 3. Диагональ делит среднюю линию на две части, каждая из которых является средней линией получившихся треугольников. $МК$ — средняя линия треугольника $ABD; MK=/$. $KN$ — средняя линия треугольника $BCD; KN=/$. Трапеция, у которой боковые стороны равны, называется равнобедренной. Свойства равнобедренной трапеции: 1. Углы при основаниях равны. 2. Диагонали в равнобедренной трапеции равны. 3. Основание высоты равнобедренной трапеции, опущенной из меньшего основания, делит другое основание на отрезки, больший из которых равен полусумме оснований. 4. Основания высот равнобедренной трапеции, опущенных из меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований. 5. Если трапеция является равнобедренной, то около неё можно описать окружность. 6. Если в равнобедренной трапеции диагонали пересекаются под прямым углом, то высота рана длине средней линии данной трапеции. В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Соотношение между сторонами и углами в прямоугольном треугольнике: В прямоугольном треугольнике $АВС$, с прямым углом $С$ Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет. Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
В прямоугольном треугольнике $АВС$ для острого угла $В$: Два многоугольника называются подобными, если их углы соответственно равны, а стороны одного многоугольника больше сходственных сторон другого многоугольника в некоторое число раз. Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного многоугольника больше сторон другого многоугольника.)
Часто встречаются задания, в которых на клетчатой бумаге изображен многоугольник и надо найти его площадь. Площадь можно вычислить несколькими способами:
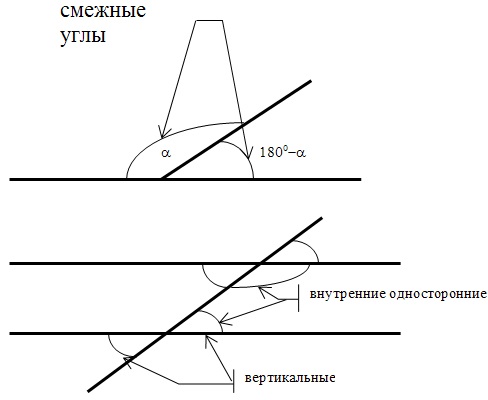
$S=/+В-1$, где $Г$ — количество узлов на границе фигуры (на сторонах и вершинах); $В$ — количество узлов внутри фигуры. Узел — это уголок клетки или пересечение линий Найдите площадь четырёхугольника, изображённого на клетчатой бумаге с размером клетки $1$ см $×$ $1$ см. Ответ дайте в квадратных сантиметрах. Отметим красными точками узлы на границе фигуры (Г), а желтыми – узлы внутри фигуры (В). Видео:Урок 6. Треугольники, четырёхугольники, многоугольники. ОГЭ. Вебинар | МатематикаСкачать  Задание №15 ОГЭ по математикеВ задании 16 проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами. По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей. Проверьте, что вы не ошибаетесь в определениях тригонометрических функций острого угла в прямоугольном треугольнике. Кроме того, убедитесь, что все данные задачи отражены на вашем чертеже. При необходимости применяйте теорему Пифагора. Если сюжет задачи развивается в равнобедренном треугольнике, то учтите, что высота, опущенная из вершины такого треугольника, делит его на два равных прямоугольных треугольника и далее задача решается в прямоугольном треугольнике. Если события происходят в окружности, то, помимо всего прочего, надо учесть, что вписанный угол равен половине центрального угла, который опирается на ту же дугу. Пусть треугольник вписан в окружность. Если этот треугольник остроугольный, то центр окружности лежит внутри треугольника. Если этот треугольник тупоугольный, то центр окружности лежит вне треугольника. А если это прямоугольный треугольник, то центр окружности лежит на середине гипотенузы. В 16 задании нам предстоит продемонстрировать свои знания в нахождении неизвестных элементов треугольника. Это могут быть углы, стороны, высоты, медианы или биссектрисы. Могут встретится задания на нахождение площади. Теория к заданию №15Так как задания №16 основаны на теории по теме «треугольники», рассмотрим базовые понятия, определения и формулы. Вначале предлагаю рассмотреть углы на плоскости: Многие задачи построены на нахождении медиан и биссектрис треугольника: Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
Средняя линия – отрезок, соединяющий середины двух сторон треугольника.
Равнобедренный треугольник — треугольник, у которого две стороны равны. Свойства равнобедренного треугольника:
Рассмотрим равносторонний треугольник: Равносторонний треугольник — треугольник, у которого все стороны равны.
Для решения этого задания достаточно знать правило — сумма углов в треугольнике равна 180°. Нам известны два угла, значит можем найти третий: 180 — 73 — 48 = 59 pазбирался: Даниил Романович | обсудить разбор | оценить Для решения этой задачи не нужно пользоваться всеми данными в условии. Для успешного решения необходимо знать, что такое средняя линия треугольника. Средняя линия — это линия соединяющая середины сторон и параллельная основанию. Средняя линия равна половине основания, которому она параллельна. Таким образом, если точки M и N являются серединами сторон AB и BC, значит эта линия параллельна AC — третьей стороне. А это в свою очередь означает, что она равна половине AC: MN =½ • AC = 64 / 2 = 32 pазбирался: Даниил Романович | обсудить разбор | оценить Если в треугольнике две стороны равны — значит он равнобедренный. А в равнобедренном треугольнике углы при основании равны. Так как сумма углов в треугольнике равна 180°, угол в вершине равен 122°, значит сумма углов при основании равна: Так как углы при основании равны, значит угол BCA равен углу BAC: 58° = ∠BCA + ∠BAC = 2 ∠BCA pазбирался: Даниил Романович | обсудить разбор | оценить Для решения этой задачи необходимо знать формулу медианы в равностороннем треугольнике, или уметь выводить её из теоремы Пифагора. В данном случае мы воспользуемся готовой формулой, и я советую вам её запомнить, чтобы не тратить время на вывод в каждом случае: Где m — медиана в равностороннем треугольнике, а a — сторона. Таким образом, для решения данной задачи подставим значение в формулу: m = ( 10√3 • √3 )/ 2 = ( 10 • 3 )/ 2 = 30 / 2 = 15 pазбирался: Даниил Романович | обсудить разбор | оценить Так как сумма углов в треугольнике равна 180°, а в прямоугольном треугольнике один из углов прямой, то сумма двух острых углов равна 90°. Отсюда можно вывести следующее правило: Сумма острых углов в прямоугольном треугольнике равна 90°. Следовательно, второй острый угол равен: pазбирался: Даниил Романович | обсудить разбор | оценить Для решения необходимо вспомнить определение медианы. Медиана — отрезок, проведенный из вершины и делящий противоположную сторону на два равных отрезка. Таким образом, медиана BM делит сторону AC (противоположную вершине B) пополам, следовательно^ AM = ½ AC = ½ 56 = 28 pазбирался: Даниил Романович | обсудить разбор | оценить Формула площади для прямоугольного треугольника выглядит следующим образом: Площадь прямоугольного треугольника равна половине произведения его катетов. Это следует из того, что один из катетов является высотой к основанию, которым является второй катет. Исходя из вышесказанного, можем решить задачу: pазбирался: Даниил Романович | обсудить разбор | оценить Вспоминаем, что в равностороннем треугольнике высота является и медианой и биссектрисой. Для медианы, а значит и для высоты, формулу я приводил чуть выше: m = ( 12√3 • √3 )/ 2 = ( 12 • 3 )/ 2 = 36 / 2 = 18 pазбирался: Даниил Романович | обсудить разбор | оценить Воспользуемся теоремой Пифагора: c² = 12² + 16² = 144 + 256 = 400 pазбирался: Даниил Романович | обсудить разбор | оценить До этого мы искали медиану, биссектрису или высоту равностороннего треугольника по формуле: Здесь же нам необходимо решить обратную задачу, найти a, если известно m. a = ( 2 • m ) / √3 = ( 2 • 11 • √3 ) / √3 = 22 pазбирался: Даниил Романович | обсудить разбор | оценить Для решения этого задания нужно помнить два факта:
Из первого пункта следует, что угол BCA = 180 — 123 = 57° Из второго — что ∠BCA = ∠BAC = 57° pазбирался: Даниил Романович | обсудить разбор | оценить В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах. Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0 pазбирался: Даниил Романович | обсудить разбор | оценить 🎦 Видео16 задание ОГЭ. 11299052. Треугольники, четырёхугольники, многоугольники и их элементыСкачать  Математика ОГЭ Задание 16. Треугольники, четырехугольники, многоугольники и их элементыСкачать  Все типы 15 задания ОГЭ 2022 математика | Геометрия на ОГЭСкачать  Математика ОГЭ Задание 16. Треугольники, четырехугольники, многоугольники и их элементыСкачать  Математика ОГЭ Задание 16. Треугольники, четырехугольники, многоугольники и их элементыСкачать  Математика ОГЭ Задание 16. Треугольники, четырехугольники, многоугольники и их элементыСкачать  Задание 16. Треугольники, четырёхугольники, многоугольники и их элементыСкачать  Математика ОГЭ. Задание 16. Треугольники, четырехугольники, многоугольники и их элементы. Углы.Скачать  Многоугольники. Математика 8 класс | TutorOnlineСкачать  Задание 15 (часть 5) | ОГЭ 2024 Математика | Четырёхугольники, многоугольники и их элементыСкачать  Задание № 15. ОГЭ - 2021. ТРЕУГОЛЬНИКИ и ЧЕТЫРЕХУГОЛЬНИКИСкачать  ОГЭ по математике 2019. Задание 16. Треугольники, четырёхугольники, многоугольники (часть 1)Скачать  Геометрия. Решение задания №15 ОГЭ: четырехугольники, многоугольники и их элементыСкачать  Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать  Математика ОГЭ Задание 16. Треугольники, четырехугольники, многоугольники и их элементыСкачать  Геометрия. Решение задания №15 ОГЭ: четырехугольники, многоугольники и их элементыСкачать  ОГЭ по математике 2021. Стрим №2. Треугольники, четырёхугольники, многоугольники и их элементы.Скачать  |
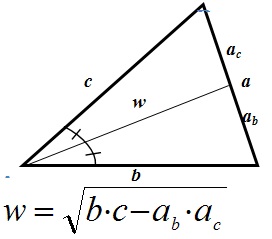 Медиана:
Медиана: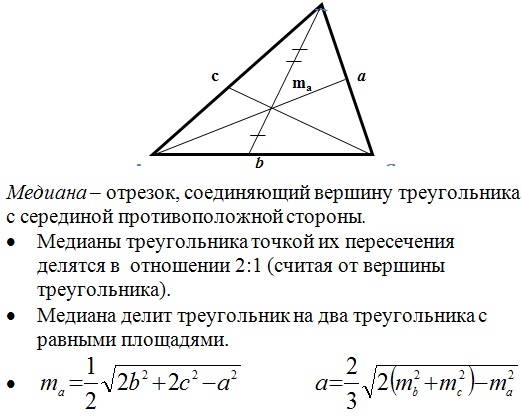 Теперь вспомним основные формулы нахождения площади треугольника:
Теперь вспомним основные формулы нахождения площади треугольника: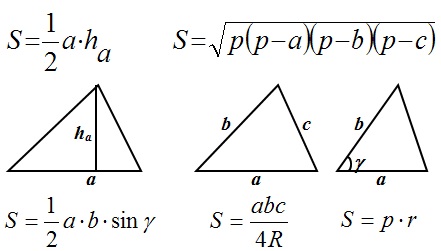 Во многих задачах встречается понятие средняя линия:
Во многих задачах встречается понятие средняя линия: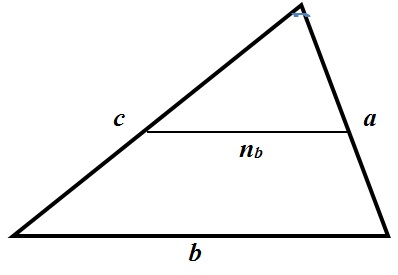 Теперь рассмотрим частные случаи треугольников — равнобедренный, равносторонний, прямоугольный. Перейдем к рассмотрению равнобедренного треугольника:
Теперь рассмотрим частные случаи треугольников — равнобедренный, равносторонний, прямоугольный. Перейдем к рассмотрению равнобедренного треугольника: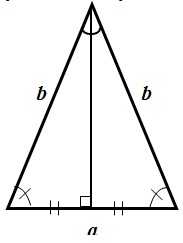
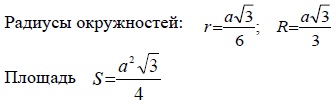 Прямоугольный треугольник:
Прямоугольный треугольник:
