В пространстве расположен параллелограмм abcd и произвольный четырехугольник a1b1c1d1 докажите (3 видео)

В пространстве расположен параллелограмм abcd и произвольный четырехугольник a1b1c1d1 докажите

Вопрос по математике:

В пространстве расположен параллелограмм abcd и произвольный четырехугольник a1b1c1d1

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Содержание

Как написать хороший ответ?
Как доказать, что четырехугольник является параллелограммом?
Определение параллелограмма
Свойства фигуры
Основные признаки
Пошаговое доказательство
💡 Видео

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Видео:№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать

Как доказать, что четырехугольник является параллелограммом?

Согласно определению,геометрическая фигура параллелограмм является четырехугольником с попарно параллельными противоположными сторонами и равными противолежащими углами. Доказать, что фигура параллелограмм позволяет как определение, так и ее признаки. Применяя на практике эти свойства, можно решать геометрические задачи разной сложности.

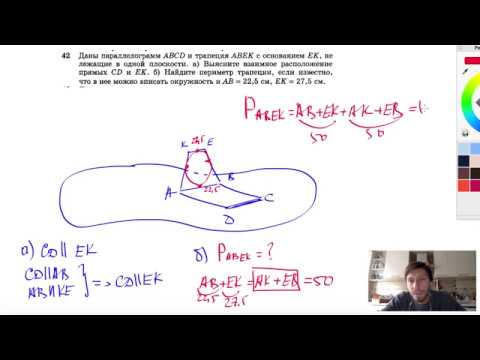
Видео:№42. Даны параллелограмм ABCD и трапеция ABEK с основанием ЕК, не лежащие в одной плоскости,Скачать

Определение параллелограмма

Четырехугольник является параллелограммом с параллельными противоположными сторонами. Эта фигура имеет по 2 тупых и острых угла, произвольную величину которых определяют при решении задач. Для этого используют не только признаки параллелограмма или треугольника, но и таблицу синусов с косинусами.

Квадрат, прямоугольник и ромб — это параллелограммы, обладающие общими свойствами. Фигура, у которой диагонали совпадают с биссектрисами, является ромбом. Согласно определению, прямоугольник — это четырехугольник, имеющий все прямые углы. Если стороны этой фигуры равны между собой, то прямоугольник является квадратом.

Параллелограмм — геометрическая фигура с равными противоположными сторонами. Если каждую из них возвести в квадрат и сложить их между собой, то полученная величина будет равна сумме квадратов диагоналей, проведенных через противоположные вершины углов фигуры. Диагонали этого четырехугольника пересекаются в точке, определить которую позволяют прямоугольные координаты.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Свойства фигуры

Зная различные свойства четырехугольников, можно решать простые и сложные задачи по геометрии, начиная с определения периметра, заканчивая нахождением координаты вершины параллелограмма. Для решения задач используют 7 основных свойств параллелограмма, учитывая что его стороны попарно образуют:

смежные углы, сумма которых составляет 180 градусов;
равные отрезки;
одинаковые по величине противоположные углы;
четырехугольник, сумма углов которого равна 360 градусов;
фигуру, диагонали которой пересекаются в точке, разделяющей их на 2 равных отрезка;
равнобедренный треугольник, одна из сторон которого является биссектрисой фигуры;
симметричные фигуры, дополняемые линией, проходящей через точку пересечения диагоналей.

Доказать последнее свойство позволяет II признак равенства треугольников. Известен отрезок, принадлежащий линии, проведенной через точку, в которой пересекаются диагонали. В четырехугольнике КМРТ он обозначен НП. Отсюда следует равенство треугольников КОП и НОР, поэтому НО=ОП.

Сумма смежных углов параллелограмма составляет 180 градусов, поскольку они являются односторонними при параллельных прямых. Существует свойство равенства острого угла и образованного высотами тупого угла четырехугольника АВСД. Параллелограмм имеет смежные углы А и Д, а высоты ВМ и ВН проведены из вершины В, поэтому угол МВН в сумме с Д равен 180 градусам.

Доказательство равенства противолежащих сторон и углов фигуры заключается в следующем. Например, диагонали ABCD делят фигуру на 2 равных треугольника, имеющих общую сторону в виде диагонали BD. При этом углы ADВ и ABC при противолежащих вершинах A и C являются накрест лежащими.

Параллелограмм состоит из равных треугольников ABD, BCD и ABC, ACD, образуемых диагоналями AC и ВD, значит AB=CD и AD=BC. Отсюда углы при вершинах A и C, В и D имеют одинаковую величину.

Свойства можно представить в виде формул для решения уравнений и примеров, а также доказать теоретически. Их следует запомнить, чтобы правильно применять на практике. Для решения более сложных задач по геометрии следует доказать основные свойства фигуры.

Видео:8 класс, 4 урок, ПараллелограммСкачать

Основные признаки

Существует 5 признаков параллелограмма, доказательство которых основано на свойствах прямых и образованных ими углов либо фигур. Выпуклый четырехугольник, вершины которого обозначены МНКП, имеет диагонали МП и НК. Признаки того, что фигура МНКП представляет собой параллелограмм, следующие:

попарное равенство противоположных сторон: МН=КП и НК=МП;
попарное равенство противоположных углов: МНК=КПМ и НКП=НМП;
равенство и параллельность противоположных сторон: МН=КП и МН||КП;
пересечение диагоналей в точке, которая делит их пополам;
МН2 + КП2 = МН2 + НК2 + КП2 + МП2

Если четырехугольник имеет 2 равные и параллельные стороны, то он представляет собой параллелограмм. Четырехугольник MNPK имеет параллельные и равные MN и KP, отсюда следует доказательство I признака:

Если провести диагональ MP, то она образует треугольники MNP и MPK.

Фигуры имеют общую сторону MP, а MN=KP по условию.

Поскольку прямая MP пересекает параллельные прямые MN и PK, то образуемые этими прямыми накрест лежащие углы равны.

Параллельность других сторон MK и NP при диагонали MP основана на равенстве накрест лежащих углов, поэтому четырехугольник MNPK — параллелограмм.

Если четырехугольник имеет противоположные стороны, которые равны попарно, то он является параллелограммом. Перед тем как доказать, что фигура является параллелограммом, следует провести диагонали. Пошаговое доказательство II признака:

Доказать деление точкой пересечения каждой из диагоналей фигуры АМКД на равные отрезки позволяет II признак равенства треугольников. При этом AОД и КОМ равны. Следовательно, AО=КО и АО=ДО.

Согласно III признаку, четырехугольник, диагонали которого пересекаются, а точка пересечения делит их пополам, представляет собой параллелограмм. В четырехугольнике MNPQ она обозначена буквой К. Поскольку в ней пересекаются диагонали MP и NQ, то образуемые ими треугольники MNК и КPQ равны по I признаку. Это следует из равенства вертикальных углов MКN и PКQ, а также MК и NК, КP и КQ, которые равны по условию.

В треугольниках MNК и КPQ стороны MN и PQ равны между собой. Углы NMК и КPQ равны как накрест лежащие при MN и PQ и секущей MP. Отсюда следует, что прямые MN||PQ. Итак, четырехугольник MNPQ — это параллелограмм по I признаку, поскольку MN и PQ равны и параллельны.

Видео:Геометрия На сторонах AB и CD параллелограмма ABCD отложены равные отрезки AM и CK. Докажите, чтоСкачать

Пошаговое доказательство

Перед тем как доказать, что четырехугольник параллелограмм, нужно провести высоты треугольников МНК и МПК, пересекающие МК в точках О и С. По данным задачи, МНК, МПК и НПК имеют одинаковые площади. Доказательство параллельности МК и НП состоит из следующих шагов:

Чтобы доказать, что МН и ПК параллельны, нужно опустить из вершин треугольников МНК и НКП высоты Н и П, которые пересекут прямую ПК в точках Р и Т. По построению НР=ПТ, а по указанному условию площади треугольников МНК и НПК совпадают. Сторона МН параллельна ПК, следовательно, МНПК — параллелограмм. Итак, порядок доказательства параллельности МН и ПК аналогичен с доказательством, что МК и НП параллельны.

Доказательство признака образования равнобедренного треугольника и трапеции при пересечении противолежащей стороны параллелограмма биссектрисой АМ одного из углов состоит из следующих утверждений:

Зная, как доказать, что фигура параллелограмм, если известно, что 2 из его сторон равны и параллельны, можно использовать I признак равенства для доказательства другого. Согласно II признаку, стороны параллелограмма попарно равны между собой.