Теорема косинусов для четырехугольника (2 видео)

Проект для НПК по математике учащегося 10 кл «Две теоремы косинусов для четырёхугольников»

Содержание

«Управление общеобразовательной организацией: новые тенденции и современные технологии»
Теорема косинусов. Доказательство теоремы косинусов.
Следствие из теоремы косинусов.
Теорема косинусов
Формулировка теоремы косинусов
Доказательство теоремы косинусов
Следствия из теоремы косинусов
Значение теоремы косинусов
🔥 Видео

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Муниципальное бюджетное общеобразовательное учреждение

«Копьёвская средняя общеобразовательная школа

с углублённым изучением отдельных предметов»

Две теоремы косинусов для четырёхугольника

Давыдович Антон Юрьевич,

учащийся 10Б класса

Загородних Ольга Иосифовна,

п. Копьёво, 2014 г.

1. Теорема косинусов для четырехугольника №1……………………………….4

2. Теорема косинусов для четырехугольника №2……………………………….5

В практике не редко возникают задачи, решение которых опирается на метрические соотношения в четырехугольнике. Так, в геодезии часто приходиться иметь с выяснением взаимного расположения четырех пунктов, в технике – с расчетами четырехзвенных шарнирных механизмов и т. п. Из всего многообразия возникших здесь вопросов нами рассматриваются лишь две теоремы, которые по аналогии с соответствующими теоремами для треугольника естественно называют теоремами косинусов для четырехугольника. Эти теоремы интересны сами по себе, богаты вытекающими из ник следствиями и могут с успехом применяться при решении различных метрических задач.

Объект исследования: две теоремы косинусов для четырехугольника.

Предмет исследования: метрические соотношения в четырехугольнике.

Гипотеза: для четырехугольника существуют теоремы, которые по аналогии с соответствующими теоремами для треугольника, называются теоремами косинусов.

Цели исследования: изучение двух теорем косинусов для четырехугольника и некоторых следствий из второй теоремы.

Задачи исследования: изучить два доказательства первой теоремы, формулировку второй и доказательства некоторых следствий из второй теоремы.

1.Теорема косинусов для четырехугольника №1

Квадрат стороны выпуклого четырехугольника равен сумме квадратов трех других сторон без удвоенных произведений пар этих сторон и косинусов углов между ними.

Учитывая, что KN 2 = а 2 , LN 2 = c 2 , после подстановки значений KL , KN , LN в равенство KL 2 = KN 2 + LN 2 – 2 KN ∙ LN cos μ, получаем

Подставим эти значения в выражение x 2 = l 2 + f 2 — b 2 – 2 ac cos μ , получим требуемое соотношение

Наиболее экономный вывод достигается средствами векторной алгебры.

Действительно, и, возведя в квадрат обе части этого равенства, получим:

Если скалярные произведения записать в виде произведения длин соответствующих векторов и косинусов углов между ними

то получим соотношение

2.Теорема косинусов для четырехугольника №2

Втора теорема косинусов (теорема Бретшнейдера, 1843 г.), редко встречается в русской и иностранной учебной литературе по элементарной геометрии.

Теорема 2. Квадрат произведения диагоналей простого четырехугольника равен сумме квадратов произведений его противоположных сторон без удвоенного произведения всех четырех сторон четырехугольника и косинуса суммы двух его противолежащих углов.

Четырехугольник называют простым , если: а) из каждой его вершины выходит две стороны; б) стороны не имеют внутренних общих точек; в) ни одна из вершин не является внутренней точкой стороны. Если хотя бы одно из этих условий не выполняется, то такой четырехугольник называют непростым. В школе изучают свойства только простых четырехугольников.

Эта теорема называется теоремой косинусов для четырехугольника потому, что она аналогична теореме косинусов для треугольника, стороны которого пропорциональны произведениям lf, ac , bd , где a , b , c , d – последовательные стороны данного четырехугольника, l и f — его диагонали. Существование такого треугольника легко может быть установлено.

3. Следствия из теоремы №2

1. Если сумма какой- либо пары противолежащих углов равна 90˚, то квадрат произведения диагоналей равен сумме квадратов произведений противолежащих сторон четырехугольника.

Действительно, если сумма углов А и С равна 90 ˚ (или же 270˚), то ( lf ) 2 = ( ac ) 2 + + ( bd ) 2 . Это соотношение представляет собой аналог теоремы Пифагора и в известном смысле может быть названа теоремой Пифагора для четырехугольника.

2. В параллелограмме с острым углом, равным 45˚, квадрат произведения диагоналей равен сумме четвертых степеней неравных сторон.

Это следствие вытекает из предыдущего при а = с и b = d .

3. Расстояние от вершины С прямого угла прямоугольного треугольника АВС
до произвольной точки D его гипотенузы выражается формулой CD 2 = (а 2 m 2 + b 2 n 2 )/с 2 , где a и b – катеты, m и n – отрезки гипотенузы АВ треугольника АВС.

4. Во всяком выпуклом четырехугольнике, вписанном в окружность, произведение диагоналей равно сумме произведений противоположных сторон (теорема Птолемея).

Во вписанном четырехугольнике сумма углов А и С равна 180˚, значит,

5. Расстояние BD между вершиной в треугольнике АВС и произвольной точкой D стороны АС определяется равенством

BD 2 = (AB 2 ∙ DC + BC 2 ∙ AD – AC ∙ AD ∙ DC).

Это соотношение известно как теорема Стюарта.

Рассмотрим вырожденный четырехугольник ABCD c углом CDA равным 180˚; диагонали его равны BD и AC = DA + DC .

Вырожденным четырехугольником называют четырехугольник ABCD , у которого вершина D лежит между вершинами А и С. Фактически здесь четырехугольник АВСВ «выродился» в треугольник с обозначенной на его стороне АС точкой D .

(BC ∙ AC) 2 = (AB ∙ DC) 2 + (BC ∙ AD) 2 – 2AB ∙ BC ∙ DC ∙ AD cos (∟B + 180˚).

Но cos (∟B + 180˚) = -cos∟B = — (AB 2 + BC 2 – AC 2 ) : (2AB ∙ BC), поэтому

BD 2 ∙ AC 2 = AB 2 ∙ DC 2 + DC 2 ∙ AD 2 + CD ∙ DA ∙ (AB 2 + BC 2 – AC 2 ), или

BD 2 ∙ AC 2 = AB 2 ∙ DC ∙ (DC + AD) + DC 2 ∙ AD ∙ (AD + CD) — CD ∙ AD ∙ AC 2 , то есть BD 2 = (AB 2 ∙ DC + BC 2 ∙ AD – BC 2 ∙ AC ∙ AD ∙ DC).

6. Если па плоскости даны четыре точки A , B , C , D , то определяемые ими шесть отрезков удовлетворяют неравенству

AB ∙ CD ≤ AC ∙ BD + AD + BC,

при чем знак равенства имеет место только в двух случаях: когда данные точки лежат на одной окружности или же эти точки лежат на одной прямой и, кроме того, пара точек А и В разделяет пару точек С и D .

В самом деле, учитывая, что

AB 2 ∙ CD 2 ≤ AC 2 ∙ BD 2 + AD 2 ∙ BC 2 + 2 AC ∙ BD ∙ AD ∙ BC ,

AB ∙ CD ≤ AC ∙ BD + AD + BC.

Если имеет место знак равенства, то ∟ B + ∟ D = 180˚ и данные четыре точки лежат на одной окружности или же на одной прямой.

Видео:9 класс, 14 урок, Теорема косинусовСкачать

Теорема косинусов. Доказательство теоремы косинусов.

Теорема косинусов — теорема евклидовой геометрии, которая обобщающает теорему Пифагора.

Теорема косинусов:

Для плоского треугольника, у которого стороны a, b, c и угол α, который противолежит стороне a, справедливо соотношение:

Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Видео:Теорема косинусов для треугольникаСкачать

Следствие из теоремы косинусов.

Теорема косинусов используется для определения cos угла треугольника:

h 2 = a 2 — (c – b cos α) 2 (2)

Приравниваем правые части уравнений (1) и (2):

b 2 — (b cos α) 2 = a 2 — (c — b cos α) 2

a 2 = b 2 + c 2 — 2bc cos α.

Если 1-н из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определить стороны b и c:

Видео:Теоремы синусов и косинусов | Ботай со мной #029 | Борис ТрушинСкачать

Теорема косинусов

Чтобы найти строну или угол треугольника применяют Теорему Косинусов.
Эта теорема обобщает теорему Пифагора. Доказать Теорему
Косинусов достаточно просто через треугольник, который
разделяют высотой на два прямоугольных треугольника.

Мы рассмотрим доказательство, формулировку,
следствия из Теоремы Косинусов.

Наряду с одной из известных теорем геометрии — теоремой Пифагора,
существует теорема косинусов. Теорема косинусов похожа по теорему
Пифагора, но отличается. Теорему косинусов, можно применить к абсолютно
любым треугольникам. А теорема Пифагора применяется исключительно
для прямоугольных треугольников.

Теорема косинусов — это теорема геометрии, обобщающая
теорему Пифагора, применяющаяся при нахождении углов
и сторон в любых треугольниках.

Видео:ТЕОРЕМА КОСИНУСОВ. Задачи на произвольные треугольникиСкачать

Формулировка теоремы косинусов

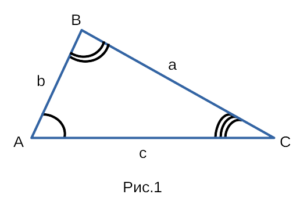
Формулировка у теоремы косинусов такая: в треугольнике квадрат любой из сторон
равен сумме квадратов двух других сторон минус удвоенное
произведение этих сторон на косинус угла между ними. Запишем эту
формулировку более кратко, используя рисунок 1, на котором изображен
произвольный треугольник ABC: ( BC^2 = AB^2 + AC^2 — 2 * (AB * AC) * cos ∠A ) .
Или, же еще более кратко: ( a^2 = b^2 + c^2 — 2bc * cos ∠A ) .

Видео:ЗАДАЧА НА ТЕОРЕМУ КОСИНУСОВСкачать

Доказательство теоремы косинусов

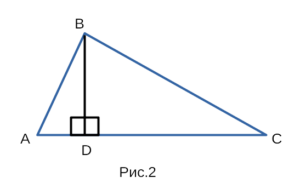
Для доказательства теоремы косинусов воспользуемся
рисунком 2, на котором изображен треугольник ABC.

Докажем, что ( BC^2 = AB^2 + AC^2 — 2 * (AB * AC) * cos ∠A: )

Доп. построение: высота BD.
Рассмотрим △BDC:
( BC^2= BD^2 + DC^2. )
Рассмотрим △ABD:
( AD = AB * cos ∠A, )
( BD = AB * sin ∠A, )
( CD = AC — AD = AC — AB cos ∠A. )
Из всего этого следует, что:
( ВС^2 = (AB * sin ∠A)^2 + (AC — AB * cos ∠A)^2 = )
( AB^2 * sin^2 ∠A + AC^2 — 2AB * AC * cos ∠A + AB^2 * cos^2 ∠A = )
( AB^2 + AC^2 — 2 * (AB*AC) * cos ∠A. )
Следовательно, ( BC^2 = AB^2 + AC^2 — 2 * (AB * AC) * cos ∠A. ) ч.т.д.
Теорема косинусов доказана.

Видео:Теорема синусов и теорема косинусовСкачать

Следствия из теоремы косинусов

Квадрат любой из сторон треугольника равен сумме квадратов двух
других сторон минус удвоенное произведение этих
сторон на косинус угла между ними.
( a^2 = b^2 + c^2 — 2bc * cos ∠A ) ;
( b^2 = c^2 + a^2 — 2ca * cos ∠B ) ;
( c^2 = a^2 + b^2 — 2ab * cos ∠C ) ;
Так, как в прямоугольном треугольнике один из углов равен 90 градусам,
следовательно теорема косинусов преобразуется в теорему Пифагора.
С помощью теоремы косинусов, можно определить косинус
любого из углов треугольника.
Если, b 2 + c 2 — a 2 > 0, ∠A будет острый.
Если b2+c2—a2= 0, ∠A будет прямым.
Если b2+c2—a2∠A будет тупым.

Видео:ТЕОРЕМА СИНУСОВ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Значение теоремы косинусов

Где применяется теорема косинусов?

Теорема косинусов применяется в тригонометрии, в частности
при нахождение сторон и углов в любых треугольниках. Например, зная
формулировку теоремы косинусов, косинус одно из угла треугольника,
и две стороны можно найти неизвестную сторону треугольника.

Виды теорем косинусов.

В зависимости от свойств треугольника, длины его сторон, градусной меры
его углов — теорема косинусов немного видоизменяется. Например, в
прямоугольных треугольниках теорема косинусов преобразуется в теорему Пифагора.