Соответственные элементы равных треугольников (6 видео)

Соответственные элементы равных треугольников

Сроки проведения: 10 декабря 2008 — 15 декабря 2008

1.Возьмем полоску бумаги.
Отметим точки A и В. Согнем по прямой АВ.

Соответственные элементы равных треугольников

2. Отметим произвольную точку С и проведем прямую АС.

Получим геометрическую фигуру — треугольник АВС. А, В, С — вершины. АВ, ВС, АС — стороны треугольника. Разогнем полоску в первоначальное положение.

3.Рассмотрим АВС и ABD.
Сравним АС и АD и углы, лежащие против этих сторон

СВА и

DВА.
При наложении они совпадают.
Аналогично АС и ВD, ВА.

Вывод: в равных треугольниках против равных сторон лежат равные углы, и обратно — против равных углов лежат равные стороны.

(Равные углы и равные стороны в равных треугольниках называются соответственными)

Определите соответственные элементы равных треугольников, полученных с помощью сгибов.

1 способ.


Сделайте намеченный сгиб.	Отметим произвольную точку О и сделайт соответствующие сгибы. Раскройте полоску.
3. Получим два равных треугольника АОВ= СОD (так как совпали при наложении).
Назовите соответственные элементы АВ СD 5= 6 АО ОС 1= 2 ВО ОD 4= 3 (так как они совпадают при наложении)

2 способ.


	Получаем АВС= MNP (так как совпали при наложении).
Назовите соответственные элементы:	NP AB M= C MN BС P= A MP АC N= B

Получаем АВС= MNP (так как совпали при наложении).

Назовите соответственные элементы:

В математике каждое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а сами рассуждения называются доказательством теоремы.

Рассмотрите:

Два треугольника, у которых равны сторона и два прилежащих к ней угла.
Соотношение между сторонами и углами произвольного треугольника.

С помощью сгибов построим два треугольника, у которых равны сторона и два прилежащих к ней угла.


Согните по намеченной линии.	Отметьте точки А и В. Отложите l = 2, 3 = 4 Прямые АМ и ВМ пересекутся в точке М. Прямые AD и BD пересекутся в точке D.
Убедитесь, что точка М и D совпали при наложении. Следовательно, АМВ= АВD

Вывод: (формулировка теоремы) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум другим прилежащим к ней углам другого треугольника, то такие треугольники равны.

Возьмите произвольный треугольник, с помощью сгибов сравните его стороны, и отметьте большую.


1. Сравните АВ и ВС.	2. ВС — часть АВ, следовательно, АВ > ВС. Выберите большую и сравните со следующей стороной.

3. Сравните АВ и АС.	4. А В — часть АС, следовательно, АС >АВ.

АС — большая сторона. ВС — меньшая сторона.

Сравните углы АВС

Содержание

Соответственные элементы равных треугольников
Медиана, биссектриса и высота треугольника
Равные треугольники
Признаки равенства треугольников
Признаки равенства треугольников
Первый признак равенства треугольников
Второй признак равенства треугольников
Третий признак равенства треугольников
📽️ Видео

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Соответственные элементы равных треугольников

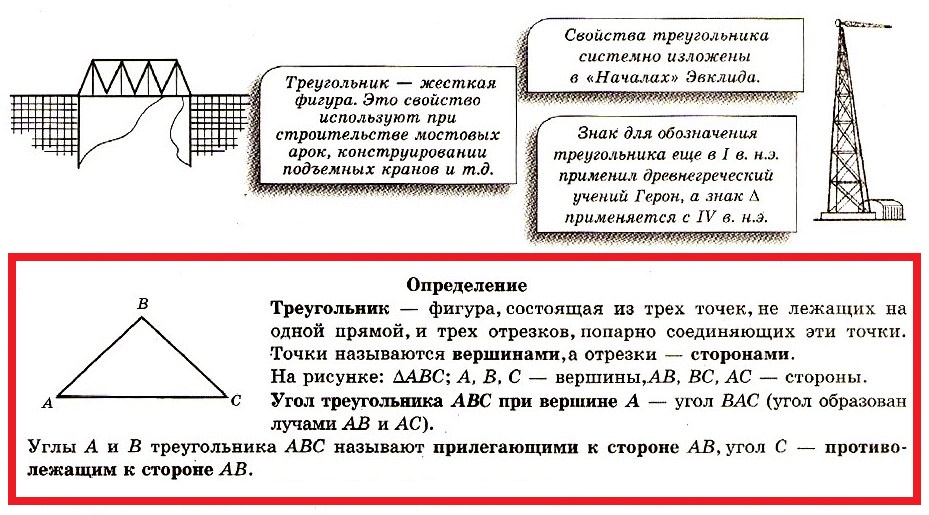
Треугольник — фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами.

Треугoльник — жесткая фигура. Это свойство используют при строительстве мостовых арок, конструировании подъемных кранов и т.д. Свойства треугольника системно изложены в «Началах» Эвклида. Знак для обозначения треугольника еще в I в. н.э. применил древнегреческий учений Герон, а знак Δ применяется с IV в. н.э.

Медиана, биссектриса и высота треугольника

Равные треугольники

Аксиома существования треугольника, равного данному.
Каким бы ни был треугольник, существует треугольник, равный ему в заданном расположении относительно данной полупрямой.

Свойства равных треугольников
1. В равных треугольниках соответствующие стороны равны.
2. В равных треугольниках соответствующие углы равны.
3. Периметры равных треугольников равны.
4. Площади равных треугольников равны.
5. Против равных сторон лежат равные углы.
6. Против равных углов лежат равные стороны.

Признаки равенства треугольников

Дополнительные признаки равенства
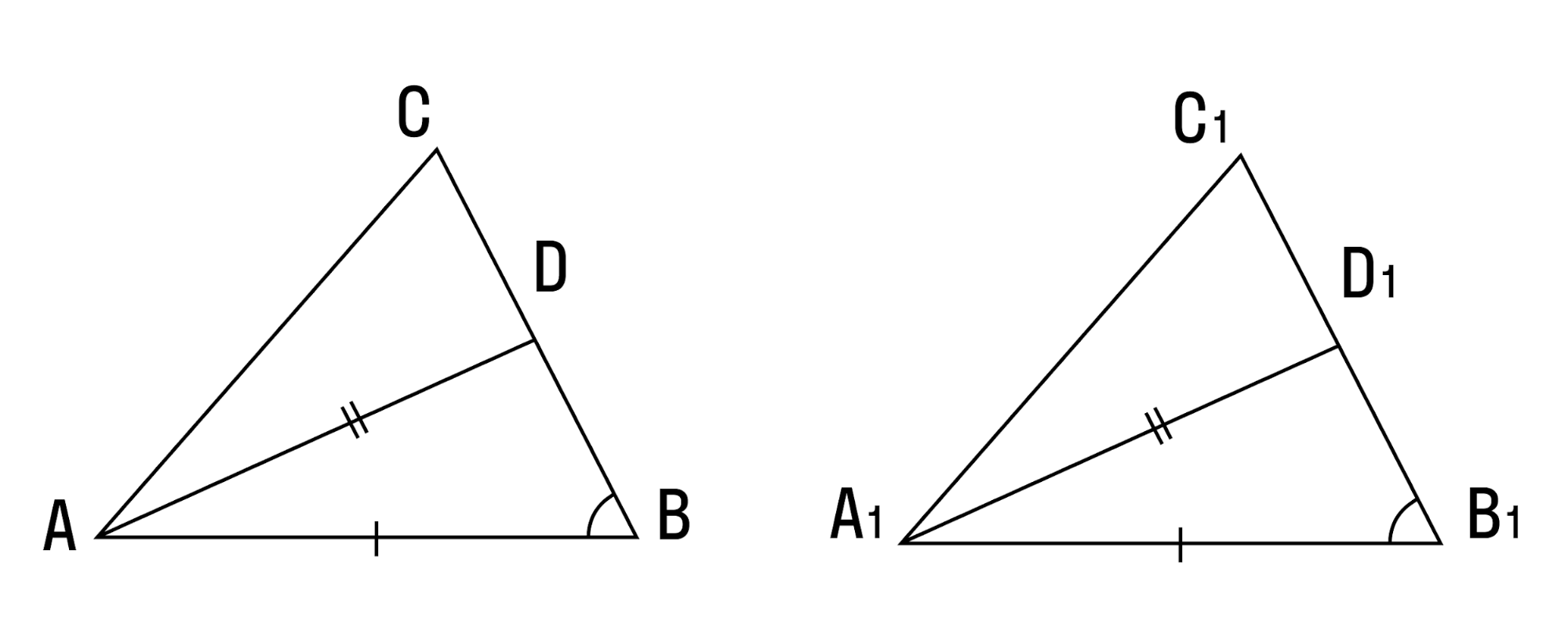
• Если две стороны и медиана, проведенная к третьей стороне треугольника, соответственно равны двум сторонам и медиане, проведенной к третьей стороне другого треугольника, такие треугольники равны.
• Если два угла и высота,проведенная к стороне, к которой прилегают эти углы, одного треугольника, соответственно равны двум углам и высоте, проведенной к стороне, к которой прилегают эти углы, другого треугольника, то такие треугольники равны.
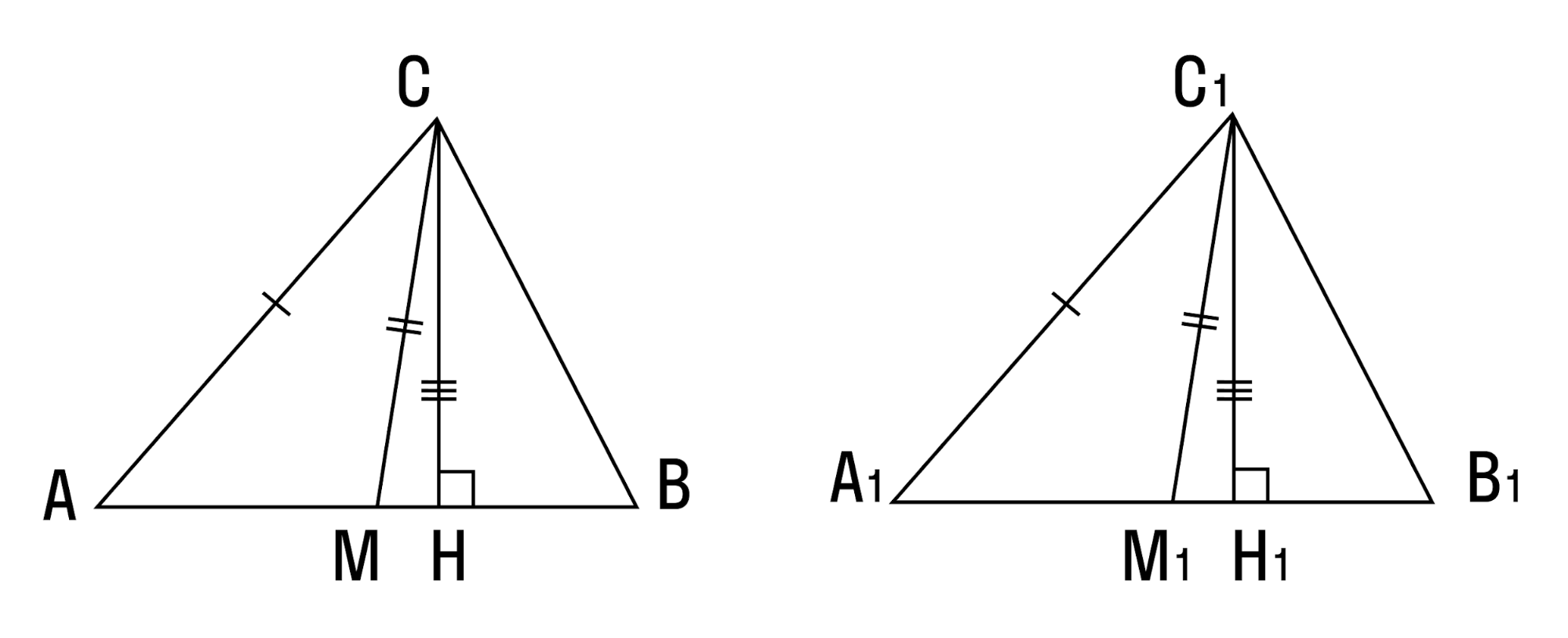
• Если сторона, высота и медиана, проведенные к стороне одного треугольника, соответственно равны стороне, высоте и медиане, проведенным к этой стороне другого треугольника, то эти треугольники равны.
• Если медиана и углы, на которые она делит угол, одного треугольника, соответственно равны медиане и углам,на которые она делит угол, другого треугольника, эти треугольники равны.

Это конспект по теме «Треугoльник. Равенство треугольников». Выберите дальнейшие действия:

Видео:Признаки равенства треугольников. 7 класс.Скачать

Признаки равенства треугольников

О чем эта статья:

Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Видео:Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Второй признак равенства треугольников

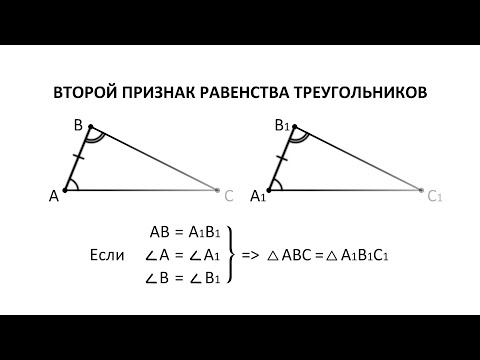
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Видео:Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

Третий признак равенства треугольников

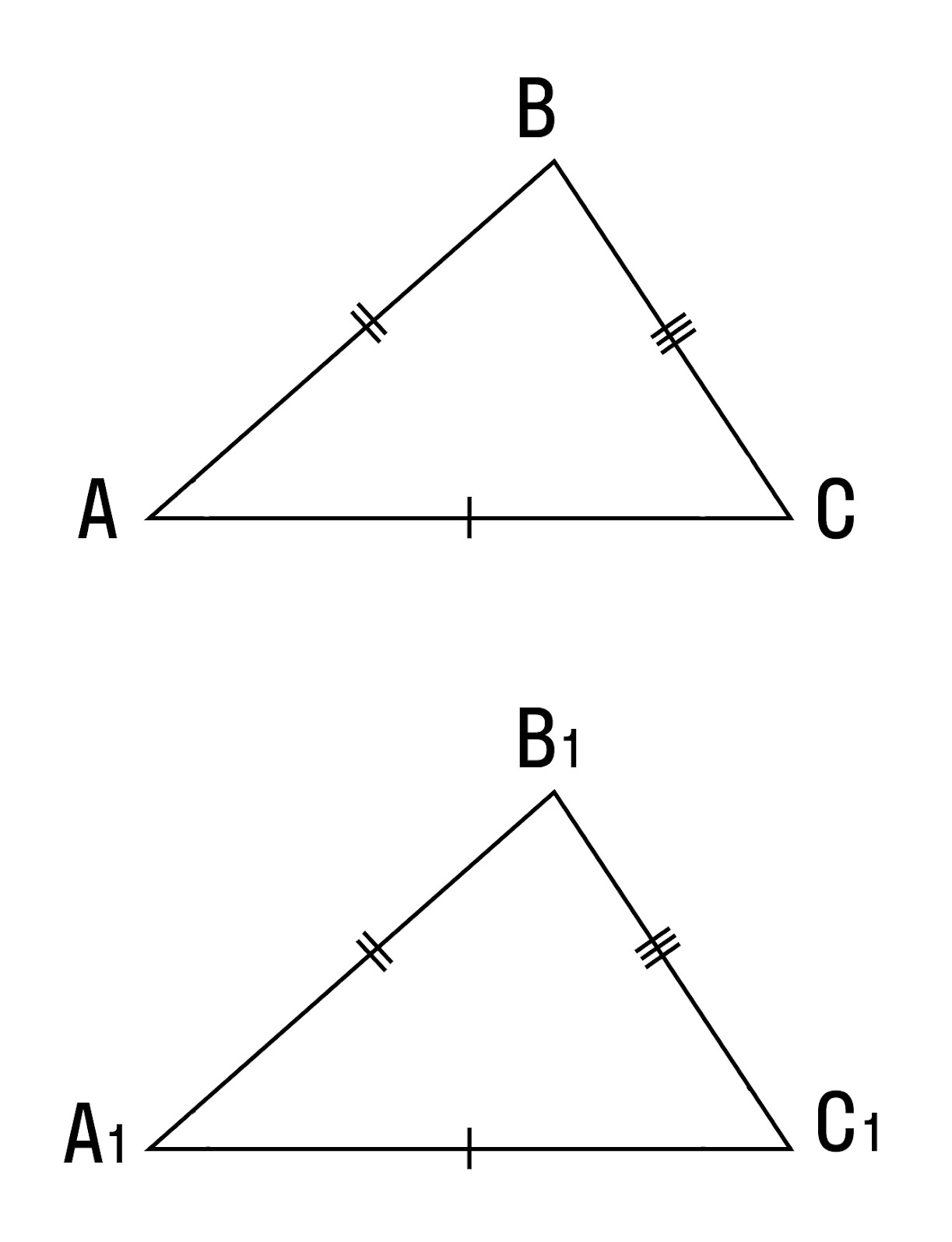
Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

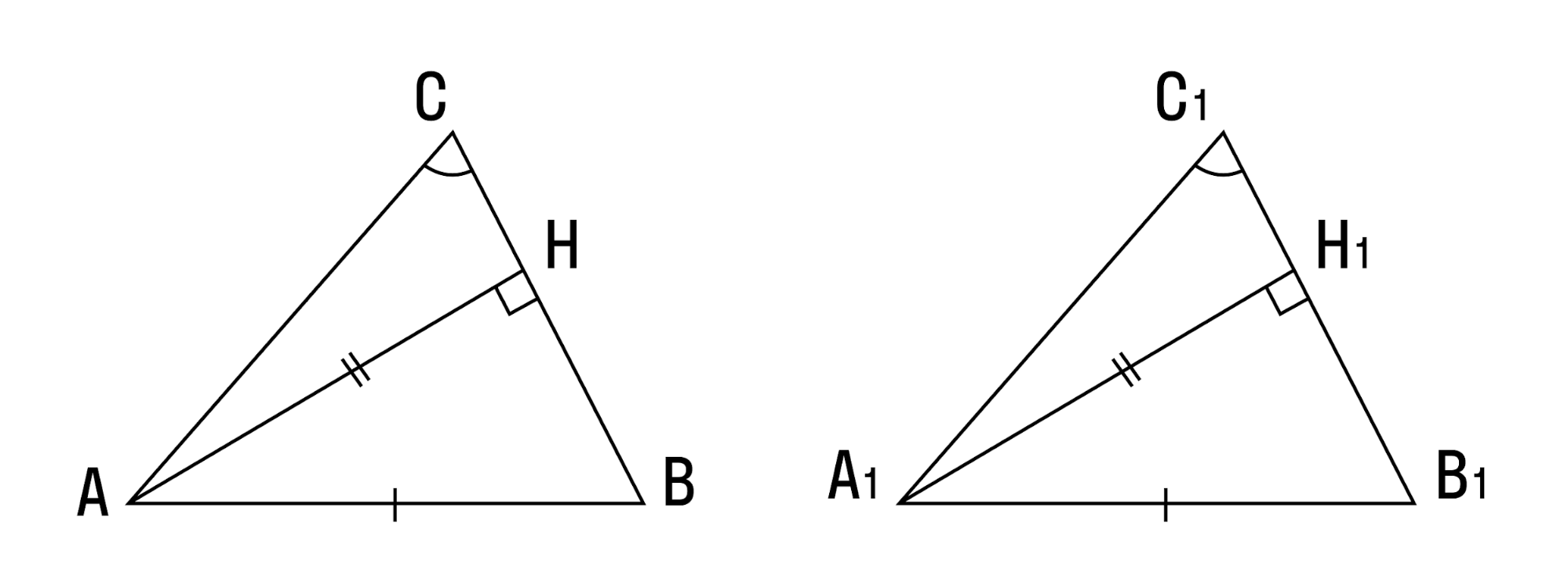
Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
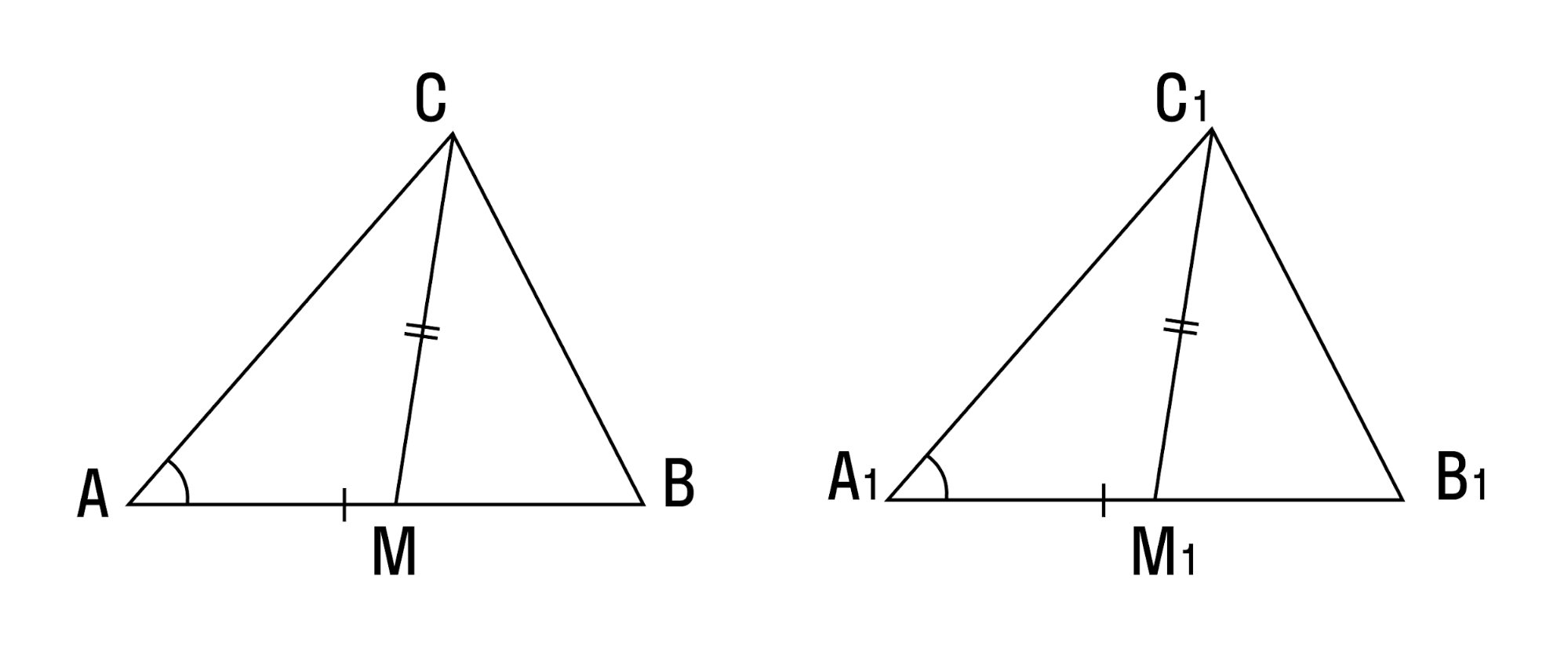
Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.