Все свойства тупоугольных треугольников (3 видео)

Тупоугольный треугольник

Содержание

Что такое тупоугольный треугольник
Элементы тупоугольного треугольника
Формулы площади тупоугольного треугольника
Пример решения задачи
Треугольник. Формулы определения и свойства треугольников.
Определение треугольника
Классификация треугольников
1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
Свойства треугольника
1.Свойства углов и сторон треугольника.
2.Теорема синусов.
3. Теорема косинусов.
4. Теорема о проекциях
Медианы треугольника
Свойства медиан треугольника:
Формулы медиан треугольника
Тупоугольный треугольник
Определения
Пример решения задачи
Что мы узнали?
📸 Видео

Видео:7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Что такое тупоугольный треугольник

Тупоугольный треугольник — геометрическая фигура на плоскости, которая представляет собой треугольник, один из углов которого является тупым, то есть больше 90º.

Такой треугольник не может быть прямоугольным и равносторонним, но может быть равнобедренным.

Сумма углов треугольника равна 180º. Именно поэтому только один из них может быть больше 90º, два других всегда острые. Это единственная особенность данной фигуры. Подход к решению задач с такой фигурой не отличается от решения задач с треугольниками других типов.

Видео:Виды треугольниковСкачать

Элементы тупоугольного треугольника

Помимо сторон и углов, тупоугольный треугольник имеет следующие элементы:

Внешний угол — тот, который смежен с внутренним, всего их шесть, по два на один внутренний. Внешний угол тупого всегда будет острым, острого — тупым.
Медиана — отрезок, который соединяет вершину треугольника с противолежащей стороной и делит ее пополам. Все медианы пересекаются друг с другом в одной точке (центроиде). Эта точка делит медианы в соотношении 2:1, считая от вершины.
Высота — перпендикуляр, который проведен из высоты треугольника на противоположную сторону. В тупоугольном треугольнике может лежать за пределами фигуры.
Биссектриса — прямая, делящая угол пополам. Делит противоположную сторону на отрезки, которые пропорциональны прилежащим сторонам фигуры. Точка, которая является пересечением биссектрис, также является центром вписанной окружности.

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Формулы площади тупоугольного треугольника

Для нахождения площади, периметра и других показателей тупоугольного треугольника используются те же формулы, что и для вычисления любого произвольного треугольника.

Площадь данной фигуры можно найти при помощи следующих формул:

S = ½ * x * h , где х — сторона;

S = √ p * ( p — x ) * ( p — y ) * ( p — z ) ,

p — полупериметр, p = ( x + y + z ) / 2

S = x * y * z / 4 * R , R — радиус описанной окружности;

S = p * r , p — полупериметр, r — радиус вписанной окружности.

Видео:Треугольники и их свойстваСкачать

Пример решения задачи

Найти площадь тупоугольного треугольника, у которого стороны равны x=9, y=5, z=6.

Для решения задачи стоит использовать формулу площади с полупериметром.

p = ( x + y + z ) / 2 , p = ( 9 + 5 + 6 ) / 2 = 20 / 2 = 10 .

S = √ p * ( p — x ) * ( p — y ) * ( p — z ) , S = √ 10 * ( 10 — 9 ) * ( 10 — 5 ) * ( 10 — 6 ) = √ 10 * 1 * 5 * 4 = √ 200 = 10 √ 2

Видео:Тупоугольный треугольник для острого умаСкачать

Треугольник. Формулы определения и свойства треугольников.

В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры — треугольника. А также разберем некоторе примеры решения задач на треугольники.

Содержание:

Видео:Треугольники: остро-, тупо- и прямоугольныеСкачать

Определение треугольника

Треугольник — это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC.

Треугольник ABC (△ABC)

Точки A, B и C — вершины треугольника. Принято писать их большими буквами.
Отрезки AB, BC и СА — стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b — β, с — γ.

Углы треугольника, также, можно обозначать специальным символом — ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Классификация треугольников

Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.

1.Разносторонний – треугольник, у которого все стороны имеют разную длину.

2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β

3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°

5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.

6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).

Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

Свойства треугольника

1.Свойства углов и сторон треугольника.

Сумма всех углов треугольника равна 180°:

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

2.Теорема синусов.

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c
sin α	=	sin β	=	sin γ

3. Теорема косинусов.

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

4. Теорема о проекциях

Для остроугольного треугольника:

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Медианы треугольника

Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника:

1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)

2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

AO	=	BO	=	CO	=	2
OD	=	OE	=	OF	=	1

3. Медиана треугольника делит треугольник на две равновеликие по площади части

4. Треугольник делится тремя медианами на шесть равновеликих треугольников.

5. Из векторов, образующих медианы, можно составить треугольник.

Формулы медиан треугольника

Формулы медиан треугольника через стороны:

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Тупоугольный треугольник

Средняя оценка: 4.6

Всего получено оценок: 108.

Средняя оценка: 4.6

Всего получено оценок: 108.

Тупоугольный треугольник мало чем отличается от обычных произвольных остроугольных треугольников, но тупой угол делает треугольник непривычным для восприятия. Это зачастую приводит в недоумение, поэтому стоит рассмотреть различные варианты решения задач на нахождение параметров тупоугольного треугольника.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Определения

Тупоугольным треугольником будет называться любой треугольник, содержащий тупой угол. Тупоугольный треугольник может быть равнобедренным, но при этом не может быть равносторонним или прямоугольным. Собственно на этом свойства этой фигуры заканчиваются. В остальном, это обычный треугольник и подход к решению таких фигур ничем не отличается.

Рис. 1. Тупоугольный треугольник.

В треугольнике сумма углов равна 180 градусам, поэтому только один угол треугольника может быть тупым, два других при этом всегда острые. Площадь тупоугольного треугольника находится так же, как площадь произвольного треугольника.

Только в тупоугольном треугольнике высота может лежать за пределами треугольника.

Рассмотрим несколько интересных задач на нахождение данных в тупоугольном треугольнике.

Видео:32. Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Пример решения задачи

Для решения любой задачи можно найти несколько способов. В данной ситуации можно пойти через площадь треугольников, достроить тупоугольный треугольник до прямоугольного или воспользоваться теоремой косинусов. Каждый из способов дает представление о том, как можно решать задачи с тупоугольным треугольником. Воспользуемся каждым из них.

Ответ в каждом случае должен быть одинаков. Но если округлять неточные ответы, то в одной задаче при одинаковых решениях можно получить разные величины. Будьте внимательны, результат не должен отличаться больше, чем на 1.

Через площадь треугольников. Площадь можно найти как половину произведения основания на высоту, проведенную к этому основанию. А можно – как половину произведения двух сторон на синус угла между ними. Нам известен косинус угла, а через косинус всегда можно найти синус.

Теперь запишем две формулы площади, выразим через них высоту и найдем ее значение.

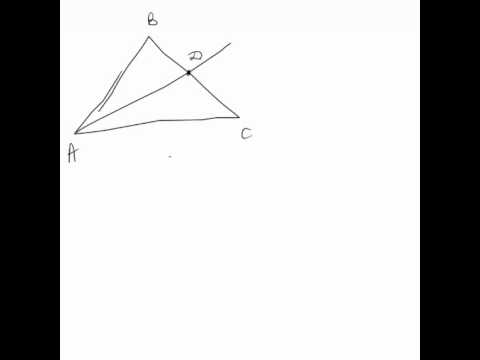
Второй способ – это достроить тупоугольный треугольник до прямоугольного. Если присмотреться, то можно заметить на чертеже два прямоугольных треугольника – это треугольники АМС и АМВ. В треугольнике АМВ можно найти косинус угла АВМ с помощью формул-приведений. Затем, через значение косинуса найти значение синуса того же угла. А синус – это отношение противолежащего катета к гипотенузе. Противолежащей катет – это искомая нами высота, а гипотенуза – это сторона АВ прямоугольного треугольника.

Тогда синус, как и в первом способе, выразим через основное тригонометрическое тождество.

Третий метод – это теорема синусов и косинусов. Для того, чтобы воспользоваться этим способом, через теорему косинусов найдем значение АС, потом через теорему синусов найдем синус угла АСВ и определим АМ из синуса угла АСВ большого прямоугольного треугольника АМС.

$$sqrt=sqrt=5$$ – по теореме косинусов.

Значение синуса угла АВС определим по основному тригонометрическому тождеству.

Выразим искомый синус угла АСВ.

Выразим из треугольника АМС и найденного значения синуса сторону АМ.

Ответы всех трех способов совпали, а, значит, задача решена верно.

Видео:ВСЕ ВИДЫ ТРЕУГОЛЬНИКОВ😉 #егэ #огэ #математика #профильныйегэ #shorts #геометрия #образованиеСкачать

Что мы узнали?

Мы поговорили об определении тупоугольного треугольника. Узнали и посмотрели на практике, какие методы решения тупоугольных треугольников существуют, а также выяснили ,какие формулы и теоремы необходимо знать для успешного решения тупоугольного треугольника.