Алгоритм построения прямоугольного треугольника (6 видео)

Урок математики «Прямоугольный треугольник»

Презентация к уроку «Прямоуголный треугольник» 3класс ПНШ

Содержание

Просмотр содержимого документа «Урок математики «Прямоугольный треугольник»»
Конспект к уроку по математике по УМК ПНШ «Прямоугольный треугольник»
Определение натуральной величины отрезка
Метод прямоугольного треугольника
Способ параллельного переноса
Поворот вокруг оси
💡 Видео

Просмотр содержимого документа
«Урок математики «Прямоугольный треугольник»»

3, 4, 5, 6, 8, 10, 12, 16, 20, 24, 32, 40

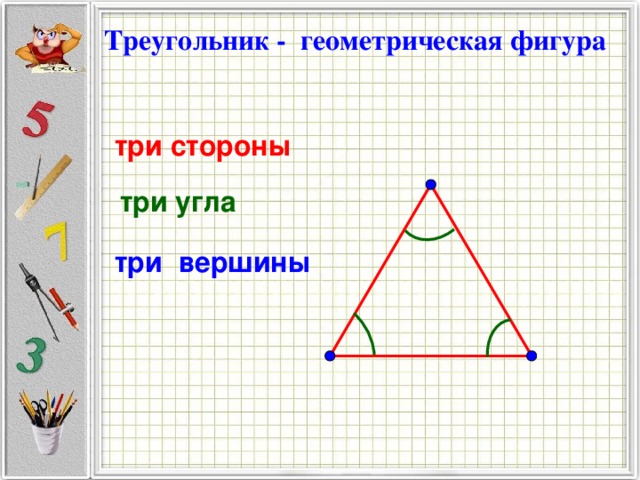
Треугольник — геометрическая фигура

УЗНАЕМ какой треугольник называется прямоугольным;

НАУЧИМСЯ чертить прямоугольный треугольник

на глаз, по заданным значениям;

ПОПРОБУЕМ применить полученные знания на практике.

у которого есть прямой угол.

Алгоритм построения прямоугольного треугольника

1. Построй прямой угол с помощью угольника.

2. Отметь на каждой стороне угла

3. Соедини эти точки отрезком.

4. Закрась полученный треугольник.

Алгоритм построения прямоугольного треугольника

1. Построй прямой угол с помощью угольника.

2. На одной стороне прямого угла отложи,

начиная от его вершины, отрезок длиной 3 см.

3. На другой стороне прямого угла отложи,

начиная от его вершины, отрезок длиной 4 см.

4. Соедини концы этих отрезков еще одним отрезком.

УЗНАЕМ какой треугольник называется прямоугольным;

НАУЧИМСЯ чертить прямоугольный треугольник

на глаз, по заданным значениям;

ПОПРОБУЕМ применить полученные знания на практике.

Видео:Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Конспект к уроку по математике по УМК ПНШ «Прямоугольный треугольник»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Тема: Прямоугольный треугольник (По УМК ПНШ)

Сформировать представление учащихся о прямоугольном треугольнике, как геометрической фигуре;

Развивать интерес к истории математических открытий;

Воспитывать уважительное отношение к соученикам, иной точке зрения.

Высказывать свою и принимать иную точку зрения;

Проявлять познавательную инициативу в оказании помощи соученикам, работая в паре и группе;

Принимать и сохранять учебную задачу;

Формировать умение контролировать свою деятельность по алгоритму, с помощью инструментов (модели прямого угла или угольника, линейки);

Формировать умение продуктивно взаимодействовать (сотрудничать с соседом по парте, в группе), способности договариваться и приходить к общему мнению;

Подводить под понятие (формулировать правило) на основе выделения существенных признаков;

Выполнять задания с использованием материальных объектов (прямоугольники, треугольники из цветного картона);

Выполнять задания на основе рисунков и схем, сделанных самостоятельно;

Строить объяснение в устной форме по предложенному плану;

Выполнять задание по заданному алгоритму;

Выдвигать гипотезы и строить логическую цепочку рассуждений при их доказательстве;

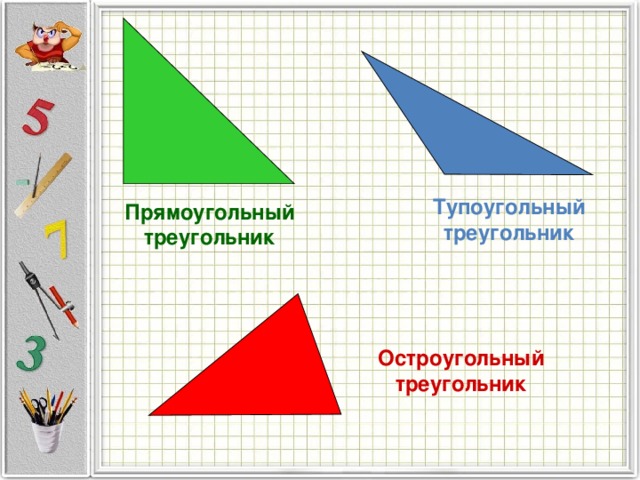
Знакомство с классификацией треугольников по величине угла (прямоугольный, тупоугольный, остроугольный);

Знакомство с понятием «прямоугольный треугольник» (треугольник, у которого есть прямой угол);

Построение прямоугольного треугольника на основе алгоритма построения прямого угла;

Освоение алгоритма построения прямоугольного треугольника по заданным катетам;

Установление существования прямоугольного треугольника со сторонами 3 см, 4 см, 5 см (Пифагорова тройка чисел: 3, 4, 5).

Методы и приемы организации деятельности учащихся: объяснение нового материала с опорой на практические действия учащихся по построению прямоугольных треугольников по заданным параметрам,индивидуальная,работа в парах, работа в группах.

Оборудование: мультимедиа, доска, презентация, учебник-1, ТПО-1, угольник, простой и цветные карандаши, модель прямоугольного треугольника со сторонами 3 см, 4 см, 5 см, модели тупоугольного и остроугольного треугольников, черновики; карточки с заданиями для групп; цветные прямоугольники.

Чекин А.Л. Математика. 3 класс: учебник в 2 ч. – М.: Академкнига/учебник, 2013 г.

Юдина Е.П. Математика: тетрадь для самостоятельных работ №1 – 3 класс. – М.:Академкнига/учебник, 2013 г.

1. Вводная часть урока

— Посмотрите на слайд

1) Что изображено?

2) Как называются эти геометрические фигуры?

3) Какая фигура лишняя и почему?

4) Что общего у треугольника и прямоугольника?

5) Сколько прямых углов у прямоугольника?

6) Есть ли прямоугольные углы в треугольнике?

7) Сколько прямых углов у треугольника?

8)Как можем проверить и доказать, что у треугольника и прямоугольника есть прямые углы? Какой инструмент поможет?

9)Четырехугольник, у которого прямые углы, называют прямоугольником. А как мы можем назвать треугольник, у которого есть прямой угол?

2 . Определение темы урока, целеполагание, мотивация

О пределите тему нашего урока?

Сегодня, мы с вами подробнее изучим прямоугольный треугольник.

Какую цель мы перед собой поставим?

Чему научимся, и что узнаем на уроке?

Чтобы нам было легче во всем разобраться, составим план наших действий:

узнать какой треугольник называют прямоугольным

научиться чертить прямоугольный треугольник

понять чем отличается прямоугольный треугольник от других видов треугольников, и как это проверить

оценить свою работу на уроке.

— Откройте содержание учебника, найдите страницу с темой урока (с.126)

Итак, №416 читает задание ______________________________

Отвечает на требование ___________________________________

— Кто может пояснить, какие треугольники называются прямоугольными?

Прямоугольный треугольник – это фигура, у которой 3 стороны, 3 угла один из которых прямой!

4. Построение прямоугольного треугольника по алгоритму

— Прочитайте задание самостоятельно.

— Сколько требований в этом задании? (4)

1.надо построить прямой угол отметить его дугой

2.на каждой стороне угла отметить по одной точке

3.соединить эти точки отрезком

4.закрасить получившийся треугольник

— Кто повторит все требования этого задания? (Слайд)

— Какой треугольник в результате построен? (прямоугольный, т.к. у него есть прямой угол)

5.Построение прямоугольного треугольника на глаз

— Прочитает задание _____________________

Постройте от руки прямоугольный треугольник на белом листе.

Проверьте свой глазомер угольником.

Поднимите руку, у кого точно получилось изобразить прямой угол?

— Предлагаю выполнить построение прямоугольного треугольника с помощью угольника на белом листе бумаги.

— Но для этого повторяем порядок построения прямоугольного треугольника

— С чего будем начинать? (С построения прямого угла по угольнику)

— Что будем делать дальше? (На сторонах угла отметим по одной точке)

— Чем завершим построение? (С помощью линейки соединим точки отрезком)

— Выполните самостоятельно построение! (помощь уч-ся, если нужна)

-Измерьте длины сторон, которые лежат на сторонах прямого угла.

Назовите их длины.

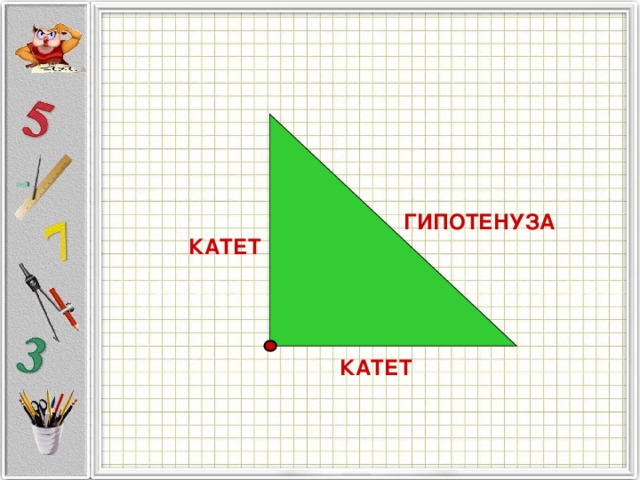
— стороны, которые лежат на сторонах прямого угла, называются КАТЕТАМИ.(Обозначьте их красным цветом К-красным,катеты!)

А теперь измерьте сторону против прямого угла, она должна быть больше чем любая из сторон-катетов. Так ли это?

— Итак, сторона, которая лежит против прямого угла, называется гипотенузой! (Г-Гипотенуза, Голубым цветом!)

— Запоминать названия сторон прямоугольного треугольника необязательно, но на математических олимпиадах эти названия иногда встречаются.

6.Построение прямоугольного треугольника по двум катетам

— Прочитайте задание. Это задание сложнее, так как заданы 2 стороны – катеты прямоуг.треугольника

-Будет ли алгоритм построения отличаться от предыдущего? (нет)

1. надо построить прямой угол отметить его дугой

2.на 1 стороне от угла отметить 3 см, поставить точку

3. на 2 стороне от угла отметить 4 см, поставить точку

3.соединить эти точки отрезком

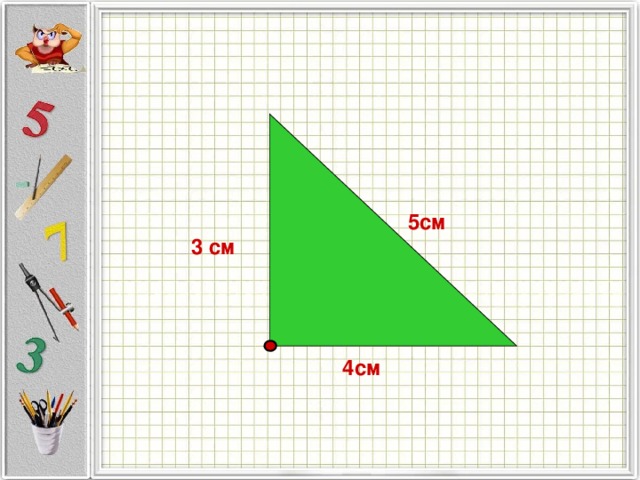
-Измерьте 3 сторону (гипотенузу) Какова ее длина? (5 см)

— Ребята, у нас получился знаменитый прямоугольный треугольник со сторонами 3 см, 4 см, 5 см.

Он называется треугольником Пифагора (или египетский треугольник). Древние египтяне не имели модели прямого угла, но при строительстве сооружений и отведении полей у них получались очень точные прямые углы. Для этого они использовали свое изобретение, египетский треугольник, и держали его в тайне.

Пифагор – это древнегреческий ученый, который жил очень давно, в 6 веке до нашей эры, т.е. больше, чем 2,5 тысячи лет тому назад, сумел разгадать секрет древних египтян и рассказать всем. Если ученики Пифагора знали, что треугольник, у которого стороны равны 3 см, 4 см и 5 см, — прямоугольный, то учащимся 21 века не знать этого просто нельзя. Это самый простой треугольник Пифагора.

Чтобы получить следующий треугольник Пифагора, нужно длину каждой стороны умножить на 2. Назовите стороны следующего треугольника Пифагора: 6 см, 8 см, 10 см, а следующего: 12 см, 16 см, 20 см. Более подробно о Пифагоре и его открытиях вы узнаете в старших классах.

7.Установление связи между прямоугольным треугольником и прямоугольником

— Прочитайте задание. Выполните

Проверь, являются ли эти треугольники прямоугольными. Обсудите с соседом, чему будут равны стороны треугольников. Измерь и запиши длины катетов и гипотенузы каждого треугольника.

Запись: АВС, АВ=3см, ВС=4см, СА=5см. АСД, СД=3см, АД=4см,АС =5см

— Таким образом, если в прямоугольнике со сторонами 3 см и 4см провести диагональ, то получатся два треугольника Пифагора с катетами 3 см и 4 см и гипотенузой 5 см.

— Вспомните тему и цели урока.

— Кто достиг своих целей?

— Что вы узнали? Чему научились?

— Откройте задний форзац (левый разворот)

— Какие бывают треугольники?

— Начертите в тетради тупоугольный треугольник

— Начертите в тетради остроугольный треугольник

9. Игра «Да-нет»: Да-хлопаем в ладоши, нет – легли на парту.

У прямоугольного треугольника есть 2 или 3 прямых угла.

Треугольник, у которого есть один прямой угол, называется прямоугольным.

Стороны треугольника, которые лежат на сторонах прямого угла, называются катетами.

Гипотенуза – это самая длинная сторона прямоугольного треугольника.

Знаменитый прямоугольный треугольник со сторонами 3 см, 4 см, 5 см называется треугольником Пифагора.

Будет ли треугольник со сторонами 6 см, 8 см и 10 см называться треугольником Пифагора.

А теперь возьмите карточки с таблицей «Плюс-минус-интересно»

Я предлагаю вам заполнить таблицу из трех граф.

В графу «П» – «плюс» вы записываете все, что понравилось на уроке, информация и задания, которые вызвали положительные эмоции.

В графу «М» – «минус» записываете все, что показалось скучным, осталось непонятным,

В графу «И» – «интересно» записываете все любопытные факты, о которых узнали на уроке и что бы еще хотелось узнать по данной теме, вопросы к учителю.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Определение натуральной величины отрезка

Если отрезок параллелен плоскости, то он проецируется на неё без искажений. В остальных случаях для нахождения его натуральной величины применяют метод прямоугольного треугольника или способы преобразования ортогональных проекций.

Видео:Построение прямоугольного треугольника по гипотенузе и острому углу.Скачать

Метод прямоугольного треугольника

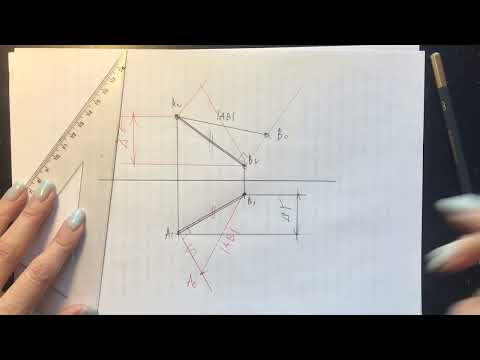
Сущность данного метода заключается в нахождении гипотенузы прямоугольного треугольника, у которого один катет равен горизонтальной (или фронтальной) проекции отрезка, а величина другого катета представляет собой разность удаления концов отрезка от горизонтальной (или, соответственно, фронтальной) плоскости проекции.

Для того чтобы найти натуральную величину отрезка AB (рисунок выше), строим прямоугольный треугольник A₀A’B’. Его первый катет A’B’ – это горизонтальная проекция AB. Второй катет A’A₀ равен величине Z_A – Z_B, то есть разности удаления точек A и B от горизонтальной плоскости П₁.

Откладываем A’A₀ = Z_A – Z_B перпендикулярно A’B’. Затем проводим гипотенузу A₀B’ треугольника A₀A’B’. На рисунке она обозначена красным цветом. Её величина соответствует настоящей длине AB.

Видео:Построение прямоугольного треугольника по 2 катетамСкачать

Способ параллельного переноса

Параллельный перенос представляет собой перемещение геометрической фигуры параллельно одной из плоскостей проекций. При этом величина проекции фигуры на эту плоскость не меняется. Например, если перемещать отрезок EF параллельно горизонтальной плоскости П₁, то длина его проекции E’F’ не изменится, когда она займет новое положение E’₁F’₁ (как это показано на рисунке ниже).

Еще одно важное свойство параллельного переноса заключается в том, что при любом перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. Если точка перемещается параллельно фронтальной плоскости, то её горизонтальная проекция движется по прямой, параллельной оси X.

Чтобы определить действительный размер отрезка EF, на свободном месте чертежа строим его новую горизонтальную проекцию E’₁F’₁ = E’F’ так, чтобы она была параллельна оси X . Затем по линиям связи находим точки E»₁ и F»₁. Расстояние между ними и есть искомая величина, поскольку мы перенесли EF в положение, параллельное фронтальной плоскости.

Метод параллельного переноса, описанный здесь, иногда называют параллельным перемещением. Посмотреть дополнительные примеры и получить более подробную информацию по данной теме можно в этой статье.

Видео:Построение прямоугольного треугольника по гипотенузе и острому углу. 7 класс. Геометрия.Скачать

Поворот вокруг оси

Для того, чтобы отрезок стал параллелен плоскости проекции и без искажения отразился на ней, он может быть повернут вокруг проецирующей прямой, проходящей через один из его концов.

Определим длину произвольного отрезка MN. Для этого через точку N проводим горизонтально проецирующую прямую i. Вокруг неё поворачиваем MN так, чтобы его проекция M’N’ заняла положение M’₁N’₁, параллельное оси X.

По линиям связи находим точку M»₁. При этом исходим из того, что M» в процессе вращения движется параллельно горизонтальной плоскости.

Точка N не изменит своего положения, так как лежит на оси поворота. Поэтому осталось только соединить N»₁ и M»₁ искомым отрезком. На рисунке он выделен красным цветом.