В треугольнике напротив большего угла

§ 30. СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА.

Теорема 1. Против большей стороны в треугольнике лежит и больший угол.

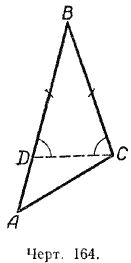
Пусть в / АВС сторона АВ больше стороны ВС. Докажем, что угол С, лежащий против большей стороны АВ, больше угла А, лежащего против меньшей стороны ВС (черт. 164).

Отложим на стороне АВ от точки В отрезок ВD, равный стороне ВС, и соединим отрезком , точки D и С.

Треугольник DВС равнобедренный. Угол ВDС равен углу ВСD, так как они лежат против равных сторон в треугольнике.

Угол ВDС — внешний угол треугольника АDС, поэтому он больше угла А.

Так как / ВСD = / ВDС, то и угол ВСD больше угла А: / ВСD > / A. Но угол ВСD составляет только часть всего угла С, поэтому угол С будет и подавно больше угла A.

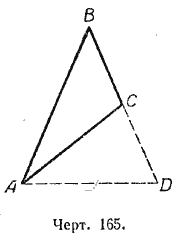
Доказать самостоятельно ту же теорему по чертежу 165, когда ВD = АВ.

В § 18 мы доказали, что в равнобедренном треугольнике углы при основании равны, т. е. в треугольнике против равных сторон лежат равные углы. Докажем теперь обратные теоремы.

Теорема 2. Против равных углов в треугольнике лежат и равные стороны.

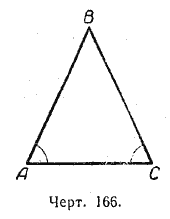
Пусть в / AВС / A = / С (черт. 166). Докажем, что AВ = ВС, т. е. треугольник АBС равнобедренный.

Между сторонами АВ и ВС может быть только одно из трёх следующих соотношений:

Докажем, что АВ > АС.

Здесь также может быть одно из трёх следующих соотношений:

1) АВ = АС;
2) АВ АС.

Если бы сторона АВ была равна стороне АС, то / С был бы равен / В. Но это противоречит условию теоремы. Значит, АВ не может равняться АС

Точно так же АВ не может быть меньше АС, так как в этом случае угол С был бы меньше угла B, что также противоречит данному условию.

Следовательно, возможен только один случай, а именно:

Мы доказали: против большего угла в треугольнике лежит и большая сторона.

Следствие. В прямоугольном треугольнике. гипотенуза больше любого из его катетов.

Теорема о соотношениях между углами и сторонами треугольника

Теорема о соотношениях между углами и сторонами
треугольника звучит так:

В треугольнике напротив большего угла лежит
большая сторона, и обратно, напротив большей
стороны лежит больший угол.

Доказательство теоремы

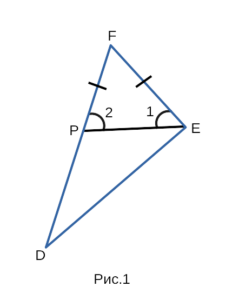
Эту теорему мы докажем, используя рисунок 1, где изображен
треугольник DFE.

1. Предположим, что в треугольнике DFE сторона FE ∠D.

Отложим на стороне DF отрезок FP = FE. В результате ∠1 = ∠2,
а сторона PF = FE, следовательно треугольник PFE — равнобедренный.

∠1 является частью ∠E, значит ∠1 ∠D. Так, как ∠1 и ∠2 равны, а ∠1
является частью ∠E, ∠2 > ∠D, значит ∠E > ∠D.

2. Допустим, что в треугольнике DFE ∠E > ∠D. Докажем,
что сторона FD > FE.

Предположим, что это не так. Тогда сторона FD = FE, или сторона FD ∠E — напротив большей стороны лежит больший угол.
Утверждение в первом и втором случае противоречит условию: ∠E > ∠D. Из этого
следует то, что наше предположение неверно, и, следовательно DF > FE, ∠E >∠D, ч.т.д.
Теорема доказана.

Следствия из доказанной теоремы

Из теоремы, которую мы сейчас доказали следует вот что:

1. Гипотенуза в прямоугольном треугольнике больше катета,
   так как катеты лежат напротив острых углов, а гипотенуза
   лежит напротив прямого угла.
2. Если две стороны или два угла треугольника равны, то
   треугольник равнобедренный, действительно, если в
   треугольнике два угла равны, значит и стороны
   напротив этих углов равны.
3. В равнобедренном треугольнике при равных сторонах два
   угла равны, а третий больший угол лежит
   напротив большей стороны.

Свойства сторон и углов треугольника

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.

a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Сумма углов треугольника равна 180°

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Величина большего угла треугольника не может быть меньшей, чем 60°.

,

где α – больший угол треугольника.

Величина меньшего угла треугольника не может быть большей, чем 60°.

,

где β – меньший угол треугольника.

,

Фигура	Рисунок	Формулировка
Треугольник
Большая сторона треугольника		Против большей стороны треугольника лежит больший угол
Больший угол треугольника		Против большего угла треугольника лежит большая сторона
Меньшая сторона треугольника		Против меньшей стороны треугольника лежит меньший угол
Меньший угол треугольника		Против меньшего угла треугольника лежит меньшая сторона
Длины сторон треугольника
		Углы треугольника
Внешний угол треугольника
Больший угол треугольника
Меньший угол треугольника
Теорема косинусов
Теорема синусов

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.

a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Сумма углов треугольника равна 180°

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Величина большего угла треугольника не может быть меньшей, чем 60°.

,

где α – больший угол треугольника.

Величина меньшего угла треугольника не может быть большей, чем 60°.

,

где β – меньший угол треугольника.

,

Треугольник
Большая сторона треугольника
	Против большей стороны треугольника лежит больший угол
Больший угол треугольника
	Против большего угла треугольника лежит большая сторона
Меньшая сторона треугольника
	Против меньшей стороны треугольника лежит меньший угол
Меньший угол треугольника
	Против меньшего угла треугольника лежит меньшая сторона
Длины сторон треугольника
	Углы треугольника
Внешний угол треугольника
Больший угол треугольника
Меньший угол треугольника
Теорема косинусов
Теорема синусов

Треугольник

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Большая сторона треугольника

Свойство большей стороны треугольника:

Против большей стороны треугольника лежит больший угол

Больший угол треугольника

Свойство большего угла треугольника:

Против большего угла треугольника лежит большая сторона

Меньшая сторона треугольника

Свойство меньшей стороны треугольника:

Против меньшей стороны треугольника лежит меньший угол

Меньший угол треугольника

Свойство меньшего угла треугольника:

Против меньшего угла треугольника лежит меньшая сторона

Длины сторон треугольника

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.

a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Углы треугольника

Свойство углов треугольника:

Сумма углов треугольника равна 180°

Внешний угол треугольника

Свойство внешнего угла треугольника:

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Больший угол треугольника

Свойство большего угла треугольника:

Величина большего угла треугольника не может быть меньшей, чем 60°.

,

где α – больший угол треугольника.

Меньший угол треугольника

Свойство меньшего угла треугольника:

Величина меньшего угла треугольника не может быть большей, чем 60°.

,

где β – меньший угол треугольника.

Теорема косинусов

Теорема синусов

Свойство меньшего угла треугольника:

,

🌟 Видео