Ключевые слова: многоугольник, правильный многоугольник, сторона, угол, вписанная, описанная окружность
Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.
Центром правильного многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон.
Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.
 |
| Около любого треугольника можно описать окружность. |
Доказательство
Дано: произвольный 
Доказать: около 
Доказательство:
1. Проведем серединные перпендикуляры к сторонам 
Точка О равноудалена от вершин 

Замечание 1
| Около треугольника можно описать только одну окружность. |
Доказательство
Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.
Замечание 2
| Около четырехугольника не всегда можно описать окружность. |
Доказательство
Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.
Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:
| В любом вписанном четырехугольнике сумма противоположных углов равна 180 0 . |
Доказательство
Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).
Углы В и D — вписанные, тогда по теореме о вписанном угле: 















Верно и обратное утверждение:
| Если сумма противоположных углов четырехугольника равна 180 0 , то около него можно описать окружность. |
Доказательство
Дано: четырехугольник АВСD, 

Доказать: около АВСD можно описать окружность.
Доказательство:
Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.
Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.
Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).





Углы ВFD и FDE — вписанные. По теореме о вписанном угле 



















Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. 




Итак, мы получили, что 




Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).
По теореме о сумме углов треугольника в 
















Подставим (3) и (4) в (2), получим:




















Примечание:
Окружность всегда можно описать:
Поделись с друзьями в социальных сетях:
🎦 Видео
Окружность, описанная около треугольника. Как найти центр и радиус. Геометрия 7-8 классСкачать

ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Центр окружности описанной вокруг треугольникаСкачать

9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Описанная окружность 1. Центр окружности, описанной около треугольника.Скачать

ОГЭ 2020 задание 17Скачать

110. Окружность, описанная около правильного многоугольникаСкачать

Задание 24 ОГЭ по математике #7Скачать

Через центр О окружности, описанной около остроугольного треугольника ДВИ МГУСкачать

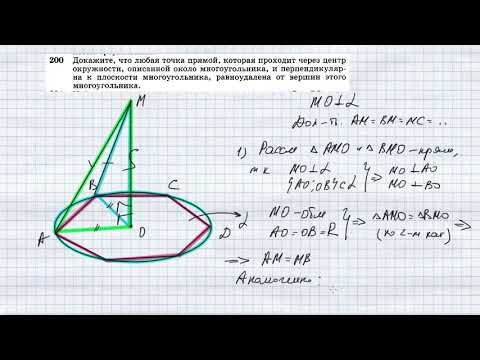
№200. Докажите, что любая точка прямой, которая проходит через центр окружности, описанной около мноСкачать
Центр окружности, описанной около треуг ABC лежит на стороне AB Радиус равен 25 Найти AC если BC=48Скачать

ОГЭ ЗАДАНИЕ 16 ЦЕНТР ОКРУЖНОСТИ ОПИСАННОЙ ОКОЛО ТРЕУГОЛЬНИКА АБС ЛЕЖИТ НА СТОРОНЕ АБ РАДИУС 14,5Скачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать





 Соединим отрезками точки O и A, O и C.
Соединим отрезками точки O и A, O и C. По свойству равнобедренного треугольника, высота и медиана, проведенные к основанию AC, совпадают):
По свойству равнобедренного треугольника, высота и медиана, проведенные к основанию AC, совпадают):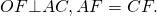
 Аналогично доказывается, что точка O лежит на серединном перпендикуляре к стороне AB.
Аналогично доказывается, что точка O лежит на серединном перпендикуляре к стороне AB.








