Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
- Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
- 1. Основные понятия и аксиомы стереометрии
- Главная > Документ
- Самостоятельная работа N 1
- Самостоятельная работа N 2
- В1. 3. ( -1) a . В2. 3. .
- Сколько пар равных векторов задаются вершинами треугольной призмы?
- Ваш ответ
- Похожие вопросы
- 💡 Видео
Видео:Разложение вектора по базису. 9 класс.Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Тема: Введение. Векторы на плоскости и в пространстве. Действия над векторами. Разложение вектора на составляющие. Полярная и декартовая система координат. Действие над векторами, заданными своими координатами .
Цель урока: Рассмотреть основные понятия векторной алгебры, правила действий над векторами, заданными своими координатами. Ввести понятие полярной системы координат.
Объяснение нового материала.
Закрепление нового материала.
Провести краткий обзор по данной дисциплине.
Начнём рассмотрение нового материала.
Определение : Отрезок называется направленным , если один из его концов считается началом отрезка, а другой—его концом.
Определение : Вектором называется направленный отрезок.
Вектор, заданный парой (А, В) несовпадающих точек, обозначается символом 
Определение : Расстояние 

Для обозначения векторов употребляются также строчные латинские буквы со стрелкой наверху: а, b, . х, у.
Определение : Вектор А А, концы которого совпадают, называется нулевым вектором.
Длина нулевого вектора равна нулю. Понятие направления для нулевого вектора не вводится.
Каждый вектор, отличный от нулевого, вполне характеризуется своим направлением и длиной.
Определение : Два вектора называются коллинеарными , если они лежат на одной прямой или на параллельных прямых.
Нулевой вектор считается коллинеарным любому вектору.
Определение : Если два ненулевых вектора а и b коллинеарные, то они могут быть направлены либо одинаково, либо противоположно. В первом случае векторы а и b называются сонаправленными ( а 

Определение : Два вектора называются равными , если они:
б) равны по модулю.
Т. е. если а= b то а 





Любой вектор равен самому себе: а=а. Если а= b и b =с, то а=с.
Откладывание вектора от данной точки.
Из любой точки плоскости а но отложить единственный вектор, равный данному вектору. Построение вектора MN, равного вектору а, называют откладыванием вектора а от точки М.
Чтобы построить вектор MN = a, проведем из точки М луч, сонаправленный с вектором а, и отложим на нем отрезок MN такой, что MN =
Задачи для самостоятельного решения:
Сколько векторов задают всевозможные упорядоченные пары точек, составленные из вершин: 1) треугольника; 2) параллелограмма?
Даны пары точек: 1) (-2; -3); (5; 4); 2) (6; -2), (13; 5); 3) (—8;—5), (—1; 1). Укажите, какие пары определяют равные векторы.
Ответ: пары 1) и 2).
3 * . Дан параллелограмм ABCD; О— точка пересечения его диагоналей. Какие пары, составленные из точек А, В, С, D и О определяют один и тот же вектор?
Действия над векторами.
а). Сложение векторов. Для того чтобы построить сумму двух данные векторов а и b, нужно выбрать произвольную точку А и отложить от неё вектор АВ=а, а затем от точки В отложить вектор ВС = b. Тогда вектор АС является искомой суммой: а+b=АВ+ ВС=АС=а.
Вектор с = а + b называют замыкающим вектором, а векторы а и b— составляющими векторами. Этот способ построения называется правилом треугольника .
Правило треугольника можно сформулировать и так: если А, В и С произвольные точки плоскости, то АВ +ВС=АС.
Это равенство называют правилом трех точек.
Сумму двух данных векторов а и b можно построить и следующим образом:
откладывая от произвольной точки О векторы ОА= а и ОВ = b, построим параллелограмм ОАСВ. Тогда вектор ОС (где [ОС>— диагональ параллелограмма) является искомой суммой: а+b=ОА+ОВ=ОА+АС=ОС=с. Этот способ построения называется правилом параллелограмма .
Для того чтобы построить сумму п данных векторов а 1, а 2 , . а n , нужно от произвольной точки О отложить вектор a 1 , затем от конца вектора а 1 отложить вектор а 2 . наконец, от конца вектора а n-1 отложить вектор а n . Тогда вектор, начало которого совпадает с началом вектора а 1, а конец — с концом вектора а n , является искомой суммой: с= а 1 + а 2 + … + а n .
б) Вычитание векторов.
Определение : Два вектора называются противоположными , если их сумма равна нулевому вектору.
Вектор, противоположный вектору а обозначают — а . Таким образом, а +(- а )=0. Ненулевые противоположные векторы имеют равные длины и противоположные направления.
Чтобы вычесть из вектора а вектор b, достаточно прибавить к вектору вектор, противоположный вектору b, т. е. a — b =a+ (- b) .
Другой способ построения разности векторов а и b состоит в следующем. Откладывая от произвольной точки О векторы ОА=а и ОС =-b (вектор, противоположный вектору b), получим ОВ==а— b.
в) Умножение вектора на число.
Определение : Произведением ненулевого вектора а на число т называется вектор, имеющий направление вектора а, если т>0 , и противоположное направление, если т . Длина этого вектора равна произведению длины вектора а на модуль числа т.
Произведение вектора а на число т обозначается та. При любых т и а векторы та и а коллинеарные и 


г) Угол между двумя векторами.
Определение : Углом между двумя ненулевыми векторами а и b называется угол между направлениями этих векторов:
(а, 
Частные случаи: 1) если а 

Прямоугольная система координат.
Определение : Прямая, на которой выбрано положительное направление и задана единица измерения длины, называется осью .
Определение : Вектор е , имеющий длину 
Пусть на плоскости задана пара взаимно перпендикулярных векторов i и j ., отложенных от некоторого начала — точки О . Такую пару векторов называют прямоугольным базисом на плоскости.
Определение : Совокупность начала О и прямоугольного базиса ( i; j ) называют прямоугольной системой координат на плоскости. Точку О называют началом координат, а вектора i и j – координатными векторами .
Определение : Вектор, направленный из начала координат в произвольную точку М плоскости хОу , называется радиусом-вектором точки М и обозначается r : ОМ = r .
Определение : Проекции вектора r на координатные оси называются координатами вектора .
Координаты радиуса-вектора r =ОМ являются одновременно координатами точки М, т. е. конца радиуса-вектора r.
Если начало вектора а=АВ не совпадает с началом координат, то координаты вектора а и координаты его конца различны. В этом случае проекции вектора а=АВ на оси координат соответственно равны х=Хв-Ха и у=Ув-Уа, т.е.
Разложение вектора по координатным осям.
Разложение вектора а в базисе ( i; j ) имеет вид
где i — единичный вектор на оси Ох, а j — единичный вектор на оси Оу . Числа х и у называются координатами вектора а в базисе (i , j).
Векторы xi и yj называются составляющими (или компонентами ) вектора а по осям координат.
Если начало вектора а находится в точке А(Ха; Уа), а конец—в точке В (Хb; Ув), то разложение вектора а записывается в виде
Правила действий над векторами, заданными своими координатами.
координаты произведения вектора на число равны произведениям соответствующих координат данного вектора на это число, т. е. ma = (mx 1 ; my 2 ).
8. Длина вектора. Расстояние между двумя точками на плоскости.
Длина радиус – вектора а = (х;у) находится по формуле

Длина вектора а = АВ = (Хв-Ха; Ув-Уа) находится по формуле

С помощью формулы (2) вычисляется также расстояние между двумя точками на плоскости.
9. Деление отрезка в данном отношении.
Если отрезок АВ разделён точкой С в отношении АС:СВ =λ , то координаты точки с находятся по формулам
Хс=
Ус=
Если λ =1, то получаются формулы для нахождения координат середины отрезка
Хс=
Ус=
10. Скалярное произведение двух векторов.
Определение : Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

Скалярное произведение векторов а=(х 1 ; у 1 ) и b=( х 2 ; у 2 ) находится по формуле:

11. Полярные координаты.
Элементами полярной системы координат являются:
луч, выходящий из точки О,— полярная ось Ор;
единица измерения длины /.
Положение точки М на плоскости задается расстоянием этой точки от полюса—длиной радиуса-вектора, выраженной в принятых единицах измерения, и углом между радиусом-вектором и полярной осью. Числа φ и г называются полярными координатами точки М, r— полярным радиусом , а φ — полярным углом . Полярные координаты точки записываются так: М( r ; φ) .
Если точка М совпадает с полюсом, то г=0, а значение φ не определено. Для любой другой точки плоскости г>0, а значение φ определяется с точностью до слагаемого, кратного 2π.
Если полюс полярной системы координат находится в начале прямоугольной системы координат, а положительная полуось Ох совпадает с полярной осью, то прямоугольные координаты точки выражаются через ее полярные координаты по формулам
Для выражения полярных координат точки через ее прямоугольные координаты используются формулы

3. После рассмотрения данной теории, разобрать решения следующих задач в тетради: Учебник Н.В. Богомолов “Практические занятия по математике” №17, №25(1), №35, №41, №58, №77.
4. Подводится итог урока. Анализируется работа учащихся.
Решить задачи №25(3), №33, №36, №64, №70, №78,
Изучить самостоятельно и выполнить конспект главы 21, § 1,2.
Практическая работа №1.
Тема: “Действия над векторами”.
Цель урока: Закрепить основные понятия векторной алгебры в ходе выполнения различных заданий. Оценить знания студентов по данной теме.
Цель урока. Проверка домашнего задания.
Сообщаю учащимся цель урока. Выполняю проверку домашнего задания на доске.
В рабочих тетрадях выполняют математический диктант.
Вопрос 1: Что называется вектором. Способы обозначения векторов.
Вопрос 2: Сформулировать определения коллинеарных векторов. Привести примеры.
Вопрос 3: Сформулировать определение соноправленных векторов. Привести примеры.
Вопрос 4: Сформулировать определение равных векторов. Привести примеры.
Вопрос 5: Сколько равных векторов можно отложить на плоскости от данной точки? Способ построения.
Вопрос 6: Что называется суммой векторов? Сформулировать правила треугольника и параллелограмма.
Вопрос 7: Что называется углом между векторами?
Вопрос 8: Сформулировать определение скалярного произведения векторов. Записать формулу вычисления скалярного произведения.
Вопрос 9: Записать условие коллинеарности, перпендикулярности векторов.
Вопрос 10: Что называется базисом на плоскости? Сформулировать определение прямоугольной системы координат.
Вопрос 11: что называется полярной системой координат? Записать формулы перехода из одной системы в другую.
Вопрос 12: Что называется длиной вектора. Записать формулу вычисления длины вектора.
Вопрос 13: Записать формулы нахождения координат середины отрезка.
В рабочих тетрадях выполняют решения задач, предложенных преподавателем.
Учебник Н.В. Богомолов “Практические занятия по математике” №118, №121, стр. 285.
После выполнения заданий рабочие тетради сдаются на проверку преподавателю. В контрольных тетрадях выполняется практическая работа. Каждый студент получает индивидуальное задание по карточкам.
Подводится итог урока. Выполняется анализ работы студентов.
Разработать кейс-папку на тему “Векторы на плоскости”.
Тема: Общее уравнение прямой и плоскости. Линии и поверхности II порядка.
Цель урока: Рассмотреть общее уравнение прямой и плоскости. Ввести определения кривых второго порядка: окружности, эллипса, гиперболы, параболы с вершиной в начале координат. Закрепит рассмотренные понятия в ходе выполнения заданий.
Цель урока. Анализ практической работы.
Объяснение нового материала.
Закрепление нового материала.
Сообщаю учащимся цель урока. Выполняю анализ практической работы.
В тетрадях записывают лекционный материал.
п.1. Общее уравнение прямой.
Определение: Уравнение первой степени относительно переменных х и у , т. е. уравнение вида
при условии, что коэффициенты А и В одновременно не равны нулю. называется общим уравнением прямой.
Отметим частные случаи общего уравнения прямой.
Проходит через начало координат Параллельна оси Ох
Параллельна оси Оу
Совпадает с осью Ох
Совпадает с осью Оу
п. 2. Векторное уравнение прямой.
Пусть l —прямая на плоскости х0у , Мо(хо,уо )— точка на этой прямой, а п=(А; В) — ненулевой вектор, перпендикулярный прямой / (он называется нормальным вектором прямой ). Возьмём точку М (х, у) — произвольная точка на прямой /, отличная от Мо. Рассмотрим вектор МоМ . Он имеет следующие координаты
Проведём радиус – векторы в каждую из данных точек : r и r 0 . Рассмотри треугольник ОМ 0 М . По правилу треугольника сложения векторов получаем:
Выразим из данного равенства вектор МоМ, получаем
Так как вектор МоМ принадлежит прямой l , а вектор п=(А; В) перпендикулярен прямой l , то данные вектора будут перпендикулярными, т.е. п┴ МоМ . По необходимому и достаточному условию перпендикулярности векторов их скалярное произведение должно быть равно нулю. Получаем равенство:
Подставим в полученное равенство вместо вектора МоМ правую часть равенства (**), получим:
Уравнение (1) называется векторное уравнение прямой .
Если его переписать в координатной форме, то получится уравнение
п. 3. Каноническое уравнение прямой.
Пусть l —прямая на плоскости х0у , Мо(хо,уо )— точка на этой прямой, а q=(m; n) — ненулевой вектор, коллинеарный прямой / (он называется направляющим вектором прямой ). Возьмём точку М (х, у) — произвольная точка на прямой /, отличная от Мо. Рассмотрим вектор МоМ . Он имеет следующие координаты
Так как вектор МоМ принадлежит прямой l , а вектор q=(m; n) коллинеарен прямой l , то данные вектора будут коллинеарными. По условию коллинеарности векторов их координаты должны быть пропорциональными. Получаем равенство:
Уравнение (2) называется каноническим уравнением прямой .
п. 4. Уравнение прямой с угловым коэффициентом.
Уравнение прямой с угловым коэффициентом имеет вид:
где k= tga – угловой коэффициент, равный тангенсу угла наклона прямой к оси Ох, а b – ордината точки пересечения прямой с осью Оу.
п.5. Условие параллельности двух прямых.
Условие параллельности прямых, заданных уравнениями с угловыми коэффициентами у = k 1 х +b 1 и у = k 2 х +b 2 имеет вид
п.6. Уравнение прямой, проходящей через две данные точки.
Уравнение прямой, проходящей через две данные точки А(х а ; у а ) и В(х в ; у в ) имеет вид:
у – у а = 
Определение: Окружностью называется множество всех точек плоскости, равноудаленных от данной точки этой плоскости, называемой центром.
Уравнение окружности с центром в начале координат и радиусом r имеет вид

Уравнение окружности с центром в точке 0 1 (а, b ) и радиусом r имеет вид

Уравнение окружности в общем виде записывается так:

где А, В. Си D — постоянные коэффициенты.
Пример: Составить уравнение окружности с центром в начале координат и радиусом, равным
Решение: Так как центр окружности находится в начале координат, то для составления уравнения
окружности используем формулу (1):
х 2 + у 2 =( 
Ответ: х 2 + у 2 =3.
Пример: Составить уравнение окружности с центром в точке (-2;-5) и радиусом равным
Решение: Так как центр окружности находится в (-2;-5), то для составления уравнения
окружности используем формулу (2):
(х-(-2)) 2 +( у-(-5)) 2 =(3) 2 или (х+2) 2 + (у+5) 2 =9.
Ответ: (х+2) 2 + (у+5) 2 =9.
Определение: Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (2а), большая расстояния между фокусами (2с).
Уравнение эллипса, фокусы которого лежат на оси Ох, имеет вид

где а— длина большой полуоси; b — длина малой полуоси (рис. ). Зависимость между параметрами а, b и с выражается соотношением

Эксцентриситетом эллипса называется отношение фокусного расстояния 2с к большой оси 2а:

Если фокусы эллипса лежат на оси Оу (рис. ), то его уравнение имеет вид

Во всех задачах на эллипс предполагается, что оси симметрии эллипса совпадают с осями координат.
Определение: Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (2а), меньшая расстояния между фокусами (2с).
Уравнение гиперболы, фокусы которой лежат на оси Ох, имеет вид

где а— длина действительной полуоси; b— длина мнимой полуоси (рис.) Зависимость между параметрами а, b и с выражается соотношением

Эксцентриситетом гиперболы называется отношение фокусного расстояния к ее действительной оси:

Гипербола имеет две асимптоты, уравнения которых

Если действительная и мнимая оси гиперболы равны (т. е. a= b ), то гипербола называется равносторонней. Уравнение равносторонней гиперболы записывается в виде

а уравнения ее асимптот

Если фокусы гиперболы лежат на оси Оу (рис. ), то ее уравнение имеет вид

а уравнения асимптот такой гиперболы

п. 4. Парабола с вершиной в начале координат.
Определение: Параболой называется множество точек на плоскости, равноудалённых от данной точки, называемой фокусом и отданной прямой, называемой директрисой.
Уравнение параболы с вершиной в начале координат, осью симметрии которой служит ось Ох и ветви направлены вправо, имеет вид

где р>0 (параметр параболы)—расстояние от фокуса до директрисы. Уравнение ее директрисы х=—р/2 . (рис. а)
Уравнение параболы с вершиной в начале координат, осью симметрии которой служит ось Ох и ветви направлены влево (рис. б), имеет вид

Уравнение ее директрисы х=р/2 .
После рассмотрения новой темы разбираем в тетрадях примеры задач из учебника Н.В. Богомолов “Практические задачи по математике”, стр. 310, №48, №74, №90.
Подводится итог урока. Анализируется работа учащихся.
Задачи из учебника №52, №72, №91.
Практическая работа №2.
Тема: Кривые второго порядка.
Цель урока: Обеспечить усвоение знаний по теме “Кривые второго порядка”. Закрепить полученные знания по данной тема. Оценить знания студентов.
Цель урока. Проверка домашнего задания.
Сообщаю учащимся цель урока. Выполняю проверку домашнего задания. Разбираю на доске задачи, вызвавшие затруднения.
Вопрос 1: Что называется общим уравнением прямой? Привести примеры.
Вопрос 2: Записать всевозможные случаи общего уравнения прямой. Привести примеры.
Вопрос 3: Сформулировать условие параллельности прямых. Привести примеры параллельных прямых.
Вопрос 4: Какие кривые второго порядка вы знаете?
Вопрос 5: Сформулировать определение окружности. Записать уравнения окружностей в зависимости от расположения центра.
Вопрос 6: Что называется эксцентриситетом эллипса? Записать формулу вычисления е .
Вопрос 7: Перечислить координаты вершин и фокусов у эллипса.
Вопрос 8: Что называется гиперболой? Записать уравнение гиперболы.
Вопрос 9: Сколько вершин у гиперболы? Записать их координаты.
Вопрос 10: Записать уравнения асимптот гиперболы.
Вопрос 11: Что называется параболой? Записать уравнение параболы, ветви которой направлены вправо; влево?
После устного опроса разбираем решение задач на доске:
Учебник Н.В. Богомолов “Практические задания по математике”, стр. 312, №55, №58, №79, №95(1).
Рабочие тетради сдаются на проверку преподавателю. В контрольных тетрадях выполняется практическая работа. Каждый студент получает индивидуальное задание по карточкам.
Подводится итог урока.
Учебник Н.В. Богомолов “Практические задания по математике”, стр. 312, №60, №81, №96.
Разработать кейс-папку по теме “Кривые второго порядка”
Тема: Предел функции. Теоремы о пределах. Два “замечательных” предела.
Цель урока: Ввести определение предела функции. Сформулировать теоремы о пределах. Рассмотреть способы вычисления пределов. Записать два “замечательных” предела.
Объяснение нового материала.
Закрепление нового материала.
Сообщаю учащимся цель урока. Выполняю анализ практической работы.
Начнём рассмотрение новой темы с рассмотрения графика функции:

Определение: Число А называется пределом функции f(x) при х → а, если для любого числа ε>0 можно указать такое δ>0, что для любого х
f(x) —A . В этом случае пишут lim f(x) =A.
Определение: Функция f(x) называется бесконечно малой при х→а, если lim f (x)=0.
Функция f(x) называется бесконечно большой при х→а, если lim f (x)=∞.
Отметим свойства бесконечно малых и бесконечно больших функций
1°. Если функции f(x) и g(х ) — бесконечно малые при х→а, то их сумма f(x)+ g(х ) при х→а также является бесконечно малой.
2°. Если функция f(x)—бесконечно малая при х→а, a F(x)—ограниченная функция, то их произведение f(x) F (х) есть функция бесконечно малая.
Следствие . Произведение конечного числа бесконечно малых функций есть величина бесконечно малая.
3°. Если при х→а функция f(x) имеет конечный предел limf(x)=A, a
функция φ (х)— бесконечно большая, то
4°. Если функция f(x) —бесконечно малая при х→а, то функция 1 /f(x) — бесконечно большая, причем предполагается, что в окрестности точки а функция f(x) не обращается в нуль. Наоборот, если при х→а функция φ (х) — бесконечно большая, то функция 1 / φ(х) — бесконечно малая.
Между бесконечно малой функцией и функцией, имеющей конечный предел, существует следующая зависимость:
Если функция f(x) имеет конечный предел при х→а, то ее можно представить в виде суммы постоянной и бесконечно малой функции при х→а. Наоборот, если функция f(x) может быть представлена в виде суммы постоянной и бесконечно малой функции при х→а, то эта функция имеет конечный предел при х→а, который равен значению постоянной.
Теоремы о пределах.
Теорема 1. Если существуют пределы функций f(x) и φ(х), то существует также и предел их суммы, равный сумме пределов функций f(x) и φ(х)
Теорема 2 . Если существуют пределы функций f(x) и φ(х) при х→а, то существует также и предел их произведения, равный произведению пределов функций f(x) и φ(х) :
Теорема 3 . Если существуют пределы функций f(x) и φ(х) при х → а и предел функции φ(х) отличен от нуля, то существует также предел отношения f(x)/ φ(х), равный отношению пределов функций f(x) и φ(х)
1 . Постоянный множитель можно вынести за знак предела:
2 . Если n —натуральное число, то
3 . Предел многочлена (целой рациональной функции)
4. Предел дробно-рациональной функции
при х→а равен значению этой функции при х=а, если а принадлежит области определения функции, т. е. lim R(x)=R(a).
Пример 1: Вычислить пределы
а) 

а) Здесь пределы числителя и знаменателя при x →0 равны нулю. Непосредственной подстановкой вместо аргумента его предельного значения вычислить предел нельзя, так как при x→0 получается отношение двух бесконечно малых величин.
Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю, и, следовательно, сделать возможным применение теоремы 3. Нужно иметь в виду, что здесь не производится сокращение на нуль, что недопустимо. По определению предела функции аргумент х стремится к своему предельному значению, никогда не принимая этого значения; поэтому до перехода к пределу можно произвести сокращение на множитель, стремящийся к нулю. Имеем
б) Пределы числителя и знаменателя при х→3 равны нулю. Разложим квадратный трехчлен в числителе на линейные множители по формуле ax 2 + bx + c = a(x—х 1 )(x—x 2 ), где х 1 и х 2 — корни трехчлена. Разложив на множители и знаменатель, сократим дробь на х-3 . Используя следствие 4, получим
в) Пределы числителя и знаменателя при х→0 равны нулю. Умножим числитель и знаменатель на сопряженный знаменателю множитель 
Пример 2: Вычислить пределы
а) 



а) Первые три слагаемых при х→ ∞ пределов не имеют, поэтому следствием 3 непосредственно воспользоваться нельзя. Вынося х 3 за скобки, получим
б) При х→∞ знаменатель 4х+1 неограниченно растет, т.е. является
величиной бесконечно большой, а обратная величина бесконечно малой. Произведение 
в) При х→ ∞ числитель и знаменатель—величины бесконечно большие. Поэтому при непосредственном применении теоремы 3 получаем выражение ∞ /∞ , которое представляет собой неопределенность. Для вычисления предела этой функции нужно числитель и знаменатель разделить
г) Разделим числитель и знаменатель на наивысшую степень аргумента в знаменателе, т.е. на х 3 :
Так как знаменатель есть величина ограниченная, то
Учащимся предлагается на закрепление решить следующие задания:
Учебник Н. В. Богомолов “Практические занятия по математике”, стр. 80, №5 — №19.
Два “замечательных” предела.
Многие пределы решаются с помощью замечательных пределов:
1) lim (1+ 

Разбираются несколько примеров на вычисление пределов с использованием первого и второго замечательного предела.
Подводится итог урока. Оценивается работа учащихся.
Разобрать примеры, рассмотренные на лекции.
Решить примеры, которые не успевают решить в классе.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

1. Основные понятия и аксиомы стереометрии
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
§ 2. САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
1. Основные понятия и аксиомы стереометрии
Самостоятельная работа N 1
1. Изобразите прямую a и точки A , B и C , не принадлежащие данной прямой. Сделайте необходимые записи.
2. Изобразите плоскость b, точки E , F , принадлежащие ей, и точку G , ей не принадлежащую. Сделайте необходимые записи.
3. Изобразите прямую a , лежащую в плоскости a. Сделайте необходимую запись.
4. Изобразите две пересекающиеся плоскости a и b. Сделайте необходимую запись.
1. Изобразите две пересекающиеся в точке O прямые a и b и точки A , B , C , причем точка A принадлежит прямой a , B принадлежит прямой b , точка C не принадлежит данным прямым.
2. Изобразите плоскость g, не принадлежащие ей точки K , L и принадлежащую ей точку M . Сделайте необходимые записи.
3. Изобразите прямую b , пересекающую плоскость b в точке O . Сделайте необходимую запись.
4. Изобразите три пересекающиеся по прямой a плоскости a, b и g. Сделайте необходимую запись.
Самостоятельная работа N 2
1. Из следующих предложений укажите аксиомы, определения, теоремы:
1) Углы при основании равнобедренного треугольника равны.
2) Через две точки пространства проходит единственная прямая.
3) Вертикальные углы равны.
4) Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
2. Определите взаимное расположение плоскостей a и b, если в них лежит треугольник ABC . Ответ обоснуйте.
3. Сколько плоскостей может проходить через три точки?
4. Найдите наибольшее число прямых, проходящих через различные пары из четырех точек.
1. Из следующих предложений укажите аксиомы, определения, теоремы:
1) Если две плоскости имеют общую точку, то они пересекаются по прямой.
2) Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
3) Для прямых и плоскостей в пространстве выполняются аксиомы планиметрии.
4) Диагонали параллелограмма точкой пересечения делятся пополам.
2. Определите взаимное расположение двух плоскостей b и g, если им принадлежат точки B и C . Ответ обоснуйте.
3. Найдите наибольшее число прямых, проходящих через различные пары из 5 точек.
4. Найдите наибольшее число плоскостей, проходящих через различные тройки из четырех точек.
2. Следствия из аксиом стереометрии
1. В плоскости двух пересекающихся прямых a и b задана точка C , не принадлежащая этим прямым. Прямая c , лежащая в данной плоскости, проходит через точку C . Как может быть расположена прямая c относительно данных прямых?
2. Даны три точки, не принадлежащие одной прямой. Докажите, что все прямые, пересекающие два из трех отрезков, соединяющих данные точки, лежат в одной плоскости.
3. Плоскость задана прямой c и не принадлежащей ей точкой C . Постройте в этой плоскости прямую a , отличную от данной прямой и не проходящую через данную точку.
4. Плоскость задана двумя пересекающимися в точке O прямыми a и b . Нарисуйте прямую c , которая пересекает данные прямые и не лежит в данной плоскости.
1. Прямая d , лежащая в плоскости треугольника ABC , пересекает его сторону AB . Каким может быть взаимное расположение прямых d и BC ?
2. В плоскости a проведены две параллельные прямые a и b . Докажите, что все прямые, пересекающие данные прямые, лежат в одной плоскости.
3. Плоскость задана двумя пересекающимися в точке O прямыми m и n . Постройте в этой плоскости прямую k , отличную от данных прямых и не проходящую через точку O .
4. Плоскость задана тремя точками D , E , F , не принадлежащими одной прямой. Нарисуйте прямую a , которая пересекает стороны DE и DF треугольника DEF и не лежит в данной плоскости.
3. Пространственные фигуры
1. Нарисуйте пятиугольную призму и разделите ее на тетраэдры.
2. Определите число вершин, ребер и граней: а) куба; б) 7-угольной призмы; в) n -угольной пирамиды.
3. Определите вид призмы, если она имеет: а) 10 вершин; б) 21 ребро; в) 5 граней.
4. Каким образом можно окрасить грани 4-угольной призмы, чтобы соседние (имеющие общее ребро) грани были окрашены в разные цвета? Какое наименьшее число цветов потребуется?
1. Нарисуйте пятиугольную пирамиду и разделите ее на тетраэдры.
2. Определите число вершин, ребер и граней: а) прямоугольного параллелепипеда; б) 6-угольнойной пирамиды; в) n -угольной призмы.
3. Определите вид пирамиды, если она имеет: а) 5 вершин; б) 14 ребер; в) 9 граней.
4. Каким образом можно окрасить грани октаэдра, чтобы соседние (имеющие общее ребро) грани были окрашены в разные цвета. Какое наименьшее число цветов потребуется?
4. Моделирование многогранников
1. Нарисуйте несколько разверток куба.
2. Нарисуйте фигуру, состоящую из четырех равных равносторонних треугольников, не являющуюся разверткой правильного тетраэдра.
3. Нарисуйте развертку правильной четырехугольной пирамиды и раскрасьте ее таким образом, чтобы при склеивании соседние грани имели разные цвета. Какое наименьшее число цветов нужно взять?
4. Нарисуйте развертку прямоугольного параллелепипеда и раскрасьте ее таким образом, чтобы при склеивании соседние грани имели разные цвета. Какое наименьшее число цветов нужно взять?
1. Нарисуйте несколько разверток правильного тетраэдра.
2. Нарисуйте фигуру, состоящую из шести квадратов, не являющуюся разверткой куба.
3. Нарисуйте развертку куба и раскрасьте ее таким образом, чтобы при склеивании соседние грани имели разные цвета. Какое наименьшее число цветов нужно взять?
4. Нарисуйте развертку правильной 6-угольной пирамиды и раскрасьте ее таким образом, чтобы при склеивании соседние грани имели разные цвета. Какое наименьшее число цветов нужно взять?
5. Параллельность прямых в пространстве
1. Запишите в правильной 4-угольнойой пирамиде SABCD все пары параллельных ребер.
2. В плоскости двух параллельных прямых a и b дана точка C , не принадлежащая этим прямым. Через точку C проведена прямая c . Как может быть расположена прямая c относительно прямых a и b .
3. Через точку, не принадлежащую данной прямой, проведите прямую, параллельную данной.
4. Найдите геометрическое место прямых, пересекающих две данные параллельные прямые.
1. Запишите четыре пары параллельных ребер куба A … D 1 .
2. Даны три прямые a , b и с . Как могут располагаться эти прямые, чтобы можно было провести плоскость, содержащую все данные прямые.
3. Даны две параллельные прямые a и b . Докажите, что любая плоскость, пересекающая одну из них, пересечет и другую.
4. Найдите геометрическое место прямых, параллельных данной прямой и пересекающих другую прямую, пересекающуюся с первой.
6. Скрещивающиеся прямые
1. В кубе A … D 1 запишите ребра, скрещивающиеся с ребром AB .
2. Запишите пары скрещивающихся ребер 4-угольной пирамиды SABCD .
3. Как расположены относительно друг друга прямые a и b на рисунке 1? Ответ обоснуйте.
4. Даны две скрещивающиеся прямые a и b и не принадлежащая им точка C . Постройте прямую c , проходящую через точку C и пересекающую прямые a и b .
1. Запишите ребра, скрещивающиеся с ребром SA правильной 4-угольной пирамиды SABCD .
2. Запишите ребра, скрещивающиеся с диагональю B 1 D куба A…D 1 .
3. Плоскости a и b пересекаются по прямой c (рис. 1). Прямая a лежит в плоскости a и пересекает прямую c . Можно ли в плоскости b провести прямую, параллельную прямой a ? Ответ обоснуйте.
4. Существуют ли две параллельные прямые, каждая из которых пересекает две данные скрещивающиеся прямые? Ответ обоснуйте.
7. Параллельность прямой и плоскости
1. Запишите ребра, параллельные плоскости грани CC 1 D 1 D правильной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 .
2. Прямая a параллельна плоскости a; прямая b пересекает плоскость a в точке B ; прямая c , пересекающая прямые a и b соответственно в точках E и F , пересекает плоскость a в точке C . Сделайте рисунок. Как могут располагаться относительно друг друга прямые a и b ?
3. Плоскости a и b пересекаются по прямой c . Точка A принадлежит плоскости a, точка B – плоскости b. Постройте: а) прямую a , лежащую в плоскости a, проходящую через точку A и параллельную плоскости b; б) прямую b , лежащую в плоскости b, проходящую через точку B и параллельную плоскости a. Как будут располагаться относительно друг друга прямые a и b ?
4. Точки A и B принадлежат смежным боковым граням пирамиды. Проведите в этих гранях через данные точки два отрезка, параллельные между собой.
1. Запишите плоскости граней, параллельных ребру CC 1 параллелепипеда A … D 1 .
2. Прямая a параллельна плоскости a; прямые b и c , пересекающие прямую a соответственно в точках B и C , пересекают плоскость a соответственно в точках D и E . Сделайте рисунок. Как могут располагаться относительно друг друга прямые a и b ?
3. Плоскости a и b пересекаются по прямой c . Прямая a лежит в плоскости a. Докажите, что если: а) a пересекает плоскость b в точке A , то A принадлежит прямой c ; б) a параллельна плоскости b, то она параллельна прямой c .
4. Точки A и B принадлежат смежным боковым граням призмы. Проведите в этих гранях через данные точки два отрезка, параллельные между собой.
8. Параллельность двух плоскостей
1. Запишите параллельные плоскости параллелепипеда A … D 1 .
2. Верны ли утверждения:
1) Через точку, не принадлежащую данной плоскости, проходит единственная плоскость, параллельная данной.
2) Если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым, лежащим в другой плоскости, то эти плоскости параллельны.
3) Существует бесконечно много прямых, параллельных данной плоскости и проходящих через точку, не принадлежащую этой плоскости.
4) Если одна из двух данных плоскостей параллельна двум пересекающимся прямым, лежащим в другой плоскости, то эти плоскости параллельны.
3. Докажите, что две плоскости, параллельные одной и той же третьей плоскости, параллельны между собой.
4. Отрезки AB и CD лежат соответственно в параллельных плоскостях a и b (рис. 2). Как могут располагаться относительно друг друга прямые AC и BD ? Могут ли они быть параллельными?
1. В треугольной пирамиде SABC проведите плоскость, параллельную ее основанию ABC .
2. Верны ли утверждения:
1) Если прямая, лежащая в одной плоскости, параллельна прямой, лежащей в другой плоскости, то эти плоскости параллельны.
2) Если плоскость пересекает две данные плоскости по параллельным прямым, то эти плоскости параллельны.
3) Существует бесконечно много плоскостей, параллельных данной прямой и проходящих через точку, не принадлежащую этой прямой.
4) Если две плоскости параллельны одной и той же прямой, то они параллельны.
3. Докажите, что если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и другую.
4. Отрезки AB и CD лежат соответственно в параллельных плоскостях a и b (рис. 3). Как могут располагаться относительно друг друга прямые AD и BC ? Могут ли они пересекаться?
9. Векторы в пространстве
1. Для данного вектора 




2. Сколько векторов задают всевозможные пары точек, составленные из вершин правильной четырехугольной пирамиды?
3. Изобразите правильный тетраэдр ABCD и нарисуйте вектор: а) 


4. Дан параллелепипед A … D 1 . Найдите сумму векторов: а) 


1. Для данного вектора 




2. Сколько векторов задают всевозможные пары точек, составленные из вершин треугольной призмы?
3. Изобразите правильный тетраэдр ABCD и нарисуйте вектор: а) 


4. Дан параллелепипед A … D 1 . Найдите сумму векторов: а) 


10. Коллинеарные и компланарные векторы
1. На какое число нужно умножить ненулевой вектор 



2. Даны два противоположно направленных вектора 





3. Дан тетраэдр ABCD . Запишите три пары его вершин, задающие компланарные векторы.
4. Дан куб A … D 1 . Запишите тройки некомпланарных векторов с началами и концами в его вершинах.
1. На какое число нужно умножить ненулевой вектор 



2. Даны два противоположно направленных вектора 





3. Дан тетраэдр ABCD . Запишите три пары его вершин, задающие некомпланарные векторы.
4. Дан куб A … D 1 . Запишите тройки компланарных векторов с началами и концами в его вершинах.
11. Параллельный перенос
1. Постройте фигуру, которая получается параллельным переносом прямой a на вектор 
2. Задайте параллельный перенос, который середину отрезка GH переводит в некоторую точку M .
3. Постройте фигуру, которая получается из квадрата ABCD параллельным переносом на вектор: а) 

4. Постройте фигуру, которая получается из тетраэдра ABCD параллельным переносом на вектор 
1. Постройте фигуру, которая получается параллельным переносом окружности с центром в точке O на вектор 
2. Задайте параллельный перенос, который точку пересечения O двух прямых a и b переводит в некоторую точку N .
3. Постройте фигуру, которая получается из правильного треугольника ABC параллельным переносом на вектор: а) 

4. Постройте фигуру, которая получается из тетраэдра ABCD параллельным переносом на вектор 
12. Параллельное проектирование
1. Сколько точек получится при параллельном проектировании двух различных точек пространства? Сделайте соответствующие рисунки и обоснование.
2. Перечислите свойства прямоугольника, которые сохраняются при параллельном проектировании.
3. Как должны быть расположены две прямые, чтобы они проектировались на плоскость в прямую и точку, не принадлежащую этой прямой?
4. Параллельные прямые a и b пересекают параллельные плоскости a и b в четырех точках. Три из них A , B и C изображены на рисунке 4. Изобразите четвертую точку D . Ответ обоснуйте.
1. Сколько точек получится при проектировании трех различных точек пространства? Сделайте соответствующие рисунки и обоснование.
2. Перечислите свойства ромба, которые сохраняются при параллельном проектировании.
3. Как должны быть расположены прямая и точка, чтобы они проектировались на плоскость в прямую и точку, принадлежащую этой прямой?
4. Пересекающиеся прямые a и b пересекают параллельные плоскости a и b в четырех точках. Три из них A , B и C изображены на рисунке 5. Изобразите четвертую точку D . Ответ обоснуйте.
13. Параллельные проекции плоских фигур
1. Изобразите параллельную проекцию прямоугольного равнобедренного треугольника, лежащего в плоскости, параллельной плоскости проектирования.
2. Изобразите параллельную проекцию равностороннего треугольника ABC и на ней постройте изображения перпендикуляров, опущенных из точки M – середины стороны AB на стороны AC и BC .
3. Изобразите параллельную проекцию правильного шестиугольника ABCDEF , взяв за исходную фигуру прямоугольник ABDE .
4. Изобразите параллельную проекцию равностороннего треугольника ABC и постройте на ней изображение перпендикуляра, опущенного из точки K – середины отрезка BO ( O – центр треугольника) на сторону AB .
1. Изобразите параллельную проекцию равностороннего треугольника, лежащего в плоскости, параллельной плоскости проектирования.
2. Изобразите параллельную проекцию квадрата ABCD и на ней постройте изображение перпендикуляров, опущенных из точки E – середины стороны BC на прямые BD и AC .
3. Изобразите параллельную проекцию правильного шестиугольника ABCDEF , взяв за исходную фигуру равносторонний треугольник ACE .
4. Изобразите параллельную проекцию прямоугольника ABCD , у которого AD = 2 AB . Постройте изображение перпендикуляра, опущенного из вершины C на диагональ BD .
14. Изображение пространственных фигур
1. Изобразите правильную четырехугольную пирамиду и ее высоту.
2. Изобразите куб, две грани которого параллельны плоскости проектирования.
3. На рисунке 6 изображена параллельная проекция куба A … D 1 . Как расположен куб относительно плоскости проектирования?
4. Дан тетраэдр ABCD . Площадь его грани ADC равна S . Найдите площадь проекции его грани BDC на плоскость ADC в направлении прямой AB .
1. Изобразите правильную треугольную пирамиду и ее высоту.
2. Изобразите куб, грани которого не параллельны плоскости проектирования.
3. На рисунке 7 изображена параллельная проекция куба A … D 1 . Как расположен куб относительно плоскости проектирования?
4. Дан тетраэдр ABCD . Площадь его грани ABD равна Q . Найдите площадь проекции его грани BDC на плоскость ADB в направлении прямой CM , где M – середина ребра AB .
15. Сечения многогранников
1. В шестиугольной призме A … F 1 (рис. 8) постройте точку пересечения прямой PQ с плоскостью ABC , где точки Q и P принадлежат соответственно боковым ребрам призмы BB 1 и DD 1 .
2. На боковых ребрах четырехугольной призмы A … D 1 заданы три точки K , L , M (рис. 9). Постройте линию пересечения плоскости KLM с плоскостью ABC .
3. Постройте сечение куба плоскостью, проходящей через точки X , Y , Z , принадлежащие соответственно ребрам AD , AA 1 , BB 1 и такие, что AX : XD = 1:2, A 1 Y : YA = 2:1, B 1 Z : ZB = 1:2.
4. В правильной пирамиде SABCD постройте сечение, проходящее через сторону основания AD и точку M , принадлежащую боковому ребру SB .
1. На боковых ребрах BB 1 и EE 1 призмы ABCDEA 1 B 1 C 1 D 1 E 1 заданы соответственно точки F и G (рис. 10). Постройте точку пересечения прямой FG с плоскостью ABC .
2. Дан куб A … D 1 . На его ребрах AA 1 , CC 1 и DD 1 заданы соответственно три точки X , Y , Z (рис. 11). Постройте линию пересечения плоскостей XYZ и ABC .
3. В правильной треугольной призме A … C 1 постройте сечение, проходящее через точки K , L и M , принадлежащие соответственно ребрам AA 1 , AC и BB 1 и такие, что: AK = KA 1 ; AL : LC = 1:2 и BM = MB 1 .
4. В правильной пирамиде SABCD постройте сечение, проходящее через диагональ AC основания и параллельное боковому ребру SD .
16. Угол между прямыми в пространстве. Перпендикулярность прямых
1. В кубе A … D 1 найдите угол между прямыми: а) AB и BB 1 ; б) BD и ВВ 1 ; в) AB 1 и CC 1 ; г) AB 1 и CD 1 .
2. В правильной треугольной призме A … C 1 отрезок CD перпендикулярен ребру AB . Найдите угол между прямыми: а) CD и AA 1 ; б) CD и A 1 B 1 .
3. В правильной четырехугольной пирамиде SABCD с равными ребрами найдите угол между диагональю AC основания и боковым ребром SC .
4. Найдите угол между скрещивающимися ребрами правильного тетраэдра.
1. В кубе A … D 1 найдите угол между прямыми: а) BC и BB 1 ; б) A 1 C 1 и AD ; в) BB 1 и BD ; г) A 1 D и BC 1 .
2. В правильной треугольной призме A … C 1 AM – медиана основания ABC . Найдите угол между прямыми: а) AM и C 1 B 1 ; б) AM и A 1 C 1 .
3. В правильном тетраэдре ABCD точка M – середина ребра CB . Найдите угол между прямыми AM и DC .
4. Найдите угол между непересекающимися ребрами правильной треугольной пирамиды.
17. Перпендикулярность прямой и плоскости
1. Докажите, что прямая, перпендикулярная плоскости, пересекает эту плоскость.
2. Через центр O квадрата ABCD проведена прямая OK , перпендикулярная плоскости этого квадрата. Докажите, что прямая AK перпендикулярна прямой BD .
3. Найдите геометрическое место точек, принадлежащих прямым, проходящим через данную точку и перпендикулярным данной прямой.
4. Точка M принадлежит боковой грани ABD треугольной пирамиды ABCD , у которой AB = BD и AC = CD . Постройте сечение этой пирамиды плоскостью, проходящей через точку M и перпендикулярной прямой AD .
1. Прямая a , перпендикулярная плоскости a, пересекает эту плоскость в точке A . Докажите, что прямая b , проходящая через точку A и перпендикулярная прямой a , лежит в плоскости a.
2. Через точку M – середину стороны AB равностороннего треугольника ABC проведена прямая MH , перпендикулярная плоскости этого треугольника. Докажите перпендикулярность прямых AB и HC .
3. Даны прямая a и не принадлежащая ей точка A . Найдите геометрическое место прямых, проходящих через точку A и перпендикулярных прямой a .
4. В прямоугольном параллелепипеде A … D 1 постройте сечение, проходящее через точку K , внутреннюю точку диагонального сечения AA 1 C 1 C , и перпендикулярное прямой BB 1 .
18. Перпендикуляр и наклонная
1. Дана плоскость a. Из точки A проведены к ней две наклонные AB = 20 см и AC = 15 см. Проекция первой наклонной на эту плоскость равна 16 см. Найдите проекцию второй наклонной.
2. Из точки M , не принадлежащей плоскости g, проведены к ней равные наклонные MA , MB и MC . Докажите, что основания наклонных принадлежат одной окружности. Найдите ее центр.
3. Из точки B проведены к плоскости b две равные по 2 см наклонные. Угол между ними равен 60 0 , а между их проекциями – 90 0 . Найдите перпендикуляр, опущенный из точки B на плоскость b.
4. Дан треугольник со сторонами 13 см, 14 см и 15 см. Точка M , не принадлежащая плоскости этого треугольника, удалена от сторон треугольника на 5 см. Найдите перпендикуляр, опущенный из точки M на плоскость данного треугольника.
1. Из точки A проведены к плоскости a наклонная AB = 9 см и перпендикуляр AO = 6 см. Найдите проекцию этого перпендикуляра на данную наклонную.
2. Найдите геометрическое место точек в пространстве, равноудаленных от всех точек данной окружности.
3. Из данной точки проведены к данной плоскости две равные наклонные, образующие между собой угол 60 0 . Угол между их проекциями – прямой. Найдите угол между каждой наклонной и ее проекцией.
4. Точка M удалена от каждой вершины правильного треугольника на 
19. Угол между прямой и плоскостью
1. В пирамиде боковые ребра одинаково наклонены к плоскости основания. В какую точку проектируется вершина пирамиды?
2. В кубе A … D 1 найдите косинус угла между ребром AA 1 и плоскостью AB 1 D 1 .
3. К плоскости a проведена наклонная MH ( H принадлежит плоскости a). Докажите, что если проекция наклонной MH образует равные углы с прямыми AH и BH , лежащими в плоскости a, то и сама наклонная MH образует с ними равные углы.
4. Проведите к данной плоскости через данную на ней точку прямую, образующую с плоскостью угол 90 0 .
1. Докажите, что в правильной пирамиде боковые ребра одинаково наклонены к плоскости основания.
2. В кубе A … D 1 найдите косинус угла между ребром A 1 D 1 и плоскостью AB 1 D 1 .
3. К плоскости b проведена наклонная BP ( P принадлежит плоскости b), которая образует равные углы с прямыми PE и PF , лежащими в плоскости b. Докажите, что углы, образованные прямыми PE и PF с проекцией наклонной BP на плоскость b, равны.
4. Через точку, не принадлежащую данной плоскости, проведите прямую, образующую с плоскостью угол 90 0 .
20. Расстояние между точками, прямыми и плоскостями
1. В прямоугольном треугольнике ABC ( 
2. В единичном кубе A … D 1 найдите расстояние между вершиной A и: а) вершиной C 1 ; б) ребром CC 1 ; в) гранью BB 1 C 1 C .
3. Точка M удалена от всех вершин прямоугольного треугольника на расстояние a . Гипотенуза треугольника равна c . Найдите расстояние от точки M до плоскости данного треугольника.
4. В кубе A … D 1 с ребром a найдите расстояние между скрещивающимися ребрами AB и B 1 C 1 .
1. Катеты прямоугольного треугольника ABC ( 
2. В единичном кубе A … D 1 найдите расстояние между вершиной D 1 и: а) вершиной B ; б) ребром AB ; в) гранью BB 1 C 1 C .
3. Из точки K на плоскость b опущен перпендикуляр длиной d и проведены две наклонные, углы которых с перпендикуляром составляют 30 0 . Угол между наклонными равен 60 0 . Найдите расстояние между основаниями наклонных.
4. В кубе A … D 1 с ребром a найдите расстояние между скрещивающимися ребрами DC и BB 1 .
21. Двугранный угол
1. Наклонная, проведенная к плоскости, равна a . Найдите ортогональную проекцию этой наклонной на плоскость, если угол между наклонной и плоскостью равен 30 0 .
2. На одной грани двугранного угла взяты две точки A и B . Из них опущены перпендикуляры AA 1 , BB 1 на другую грань и AA 2 , BB 2 на ребро двугранного угла. Найдите BB 2 , если AA 1 = 6 см, BB 1 = 3 см, AA 2 = 24 см.
3. Два равных прямоугольника имеют общую сторону и их плоскости образуют угол 45 0 . Найдите отношение площадей двух фигур, на которые ортогональная проекция стороны одного прямоугольника разбивает другой.
4. Докажите, что перпендикуляры, проведенные из точек данной прямой на плоскость, лежат в одной плоскости и геометрическим местом оснований этих перпендикуляров является линия пересечения этих плоскостей.
1. Наклонная, проведенная к плоскости, равна a . Найдите ортогональную проекцию этой наклонной на плоскость, если угол между наклонной и плоскостью равен 60 0 .
2. На одной грани двугранного угла взяты две точки, отстоящие от его ребра на 9 см и 12 см. Расстояние от первой точки до другой грани двугранного угла равно 20 см. Найдите расстояние от этой грани до второй точки.
3. Два равнобедренных треугольника имеют общее основание, а их плоскости образуют угол 60 0 . Общее основание равно 16 см, боковая сторона одного треугольника равна 17 см, а боковые стороны другого перпендикулярны. Найдите расстояние между вершинами треугольников, лежащими против общего основания.
4. Докажите, что точка пересечения ортогональных проекций двух прямых на плоскость является ортогональной проекцией точки пересечения данных прямых на ту же плоскость.
22. Перпендикулярность плоскостей
1. Дан куб A … D 1 . Докажите перпендикулярность плоскостей: а) ABD и DCC 1 ; б) AB 1 C 1 и ABB 1 .
2. Через данную прямую, лежащую в данной плоскости, проведите плоскость, перпендикулярную этой плоскости.
3. Две перпендикулярные плоскости a и b пересекаются по прямой AB . Прямая CD лежит в плоскости a, параллельна AB и находится на расстоянии 60 см от нее. Точка E принадлежит плоскости b и находится на расстоянии 91 см от AB . Найдите расстояние от точки E до прямой CD .
4. Докажите, что прямая a и плоскость a, перпендикулярные одной и той же плоскости b, параллельны, если прямая a не лежит в плоскости a.
1. Дан куб A … D 1 . Докажите перпендикулярность плоскостей: а) AA 1 D 1 и D 1 B 1 C 1 ; б) A 1 B 1 D и BB 1 C 1 .
2. Через наклонную к плоскости проведите плоскость, перпендикулярную этой плоскости.
3. Отрезок MN имеет концы на двух перпендикулярных плоскостях и составляет с ними равные углы. Докажите, что точки M и N одинаково удалены от линии пересечения данных плоскостей.
4. Докажите, что две плоскости a и b параллельны, если они перпендикулярны плоскости g и пересекают ее по параллельным прямым.
23*. Центральное проектирование
Самостоятельная работа N 1
1. Куда при центральном проектировании переходит прямая, параллельная плоскости проектирования?
2. Плоская фигура лежит в плоскости, параллельной плоскости проектирования, и находится между центром и плоскостью проектирования. Как при этом определяется коэффициент подобия фигуры и ее проекции?
3. Радиус основания конуса равен R . Через середину высоты проведена плоскость, параллельная основанию. Найдите площадь сечения.
4. В треугольной пирамиде ABCD (рис. 12) через точки M и N , принадлежащие соответственно граням ABD и BCD , проведите сечение, параллельное ребру AC .
1. В каком случае центральной проекцией двух прямых будут две параллельные прямые?
2. Плоская фигура лежит в плоскости, параллельной плоскости проектирования. Плоскость проектирования расположена между центром проектирования и плоскостью данной фигуры. Как при этом определяется коэффициент подобия фигуры и ее проекции?
3. Радиус основания конуса равен R . Он пересечен плоскостью, параллельной основанию и делящей высоту конуса в отношении m : n , считая от вершины. Найдите площадь сечения.
4. В треугольной пирамиде ABCD (рис. 13) через точку M , принадлежащую высоте пирамиды DO , проведите сечение, параллельное грани BCD .
Самостоятельная работа N 2
1. Прямая m пересекает плоскость проектирования p и не проходит через центр проектирования S . Изобразите центральную проекцию части данной прямой, расположенной в одном полупространстве с точкой S относительно плоскости p.
2. Изобразите центральную проекцию куба A … D 1 на плоскость, параллельную плоскости AA 1 C 1 .
3. Изобразите центральную проекцию правильной шестиугольной призмы на плоскость, параллельную ее основаниям.
4. Дана правильная четырехугольная пирамида SABCD , у которой двугранный угол при основании равен 60 0 . Найдите расстояние между прямыми AB и SC , если AB = 1.
1. Прямая m пересекает плоскость проектирования p и не проходит через центр проектирования S . Изобразите центральную проекцию части данной прямой, расположенной в разных полупространствах с точкой S относительно плоскости p.
2. Изобразите центральную проекцию куба A … D 1 на плоскость, параллельную плоскости AB 1 C 1 .
3. Изобразите центральную проекцию правильной шестиугольной призмы на плоскость, не параллельную ее основаниям.
4. Дана правильная треугольная призма A … C 1 , все ребра которой равны 1. Найдите расстояние между прямыми AA 1 и BC 1 .
24. Многогранные углы
1. Запишите, при каких условиях углы a, b и g могут быть плоскими углами трехгранного угла.
2. В трехгранном угле все плоские углы прямые. На его ребрах от вершины отложены отрезки 2 см, 4 см, 6 см и через их концы проведена плоскость. Найдите площадь получившегося сечения.
3. По скольким прямым попарно пересекаются плоскости всех граней четырехгранного угла?
1. Два плоских угла трехгранного угла равны a и b, причем a > b. Запишите, в каких границах возможны значения третьего плоского угла g данного трехгранного угла.
2. В трехгранном угле все двугранные углы – прямые. Из вершины этого угла в его внутренней области проведен отрезок, проекции которого на ребра равны a , b и c . Найдите данный отрезок.
3. По скольким прямым попарно пересекаются плоскости всех граней пятигранного угла?
25*. Выпуклые многогранники
1. Определите число вершин (В), ребер (Р) и граней (Г) n -угольной призмы: а) выпуклой; б) невыпуклой.
2. Нарисуйте выпуклый многогранник с 5 вершинами.
3. В выпуклом многограннике известно число граней Г, причем каждая грань имеет одно и то же число сторон n . Найдите число: а) плоских углов ( 

4. Выпуклый многогранник имеет В вершин, Р ребер и Г граней. От него отсекли m -гранный угол. Найдите число вершин, ребер и граней полученного многогранника.
1. Определите число вершин (В), ребер (Р) и граней (Г) n -угольной пирамиды: а) выпуклой; б) невыпуклой.
2. Нарисуйте выпуклый многогранник с 6 вершинами.
3. В выпуклом многограннике известно число вершин В, причем в каждой вершине сходится одно и то же число ребер m . Найдите число: а) плоских углов ( 

4. Выпуклый многогранник имеет В вершин, Р ребер и Г граней. К его n -угольной грани пристроили пирамиду. Найдите число вершин, ребер и граней нового многогранника.
26*. Теорема Эйлера
1. Нарисуйте невыпуклый многогранник, для которого выполняется теорема Эйлера.
2. Докажите, что для всякого выпуклого многогранника справедливо соотношение 

4. Найдите сторону основания правильной треугольной пирамиды с высотой h и боковым ребром b .
1. Нарисуйте невыпуклый многогранник, для которого не выполняется теорема Эйлера.
2. Докажите, что для всякого выпуклого многогранника справедливо соотношение 

4. Найдите высоту правильной треугольной пирамиды со стороной основания a и высотой боковой грани h .
27. Правильные многогранники
1. Нарисуйте: а) развертку тетраэдра; б) многогранник, двойственный гексаэдру.
2. Постройте сечение октаэдра плоскостью, проходящей через одну из его вершин и середины двух параллельных ребер, которым не принадлежит данная вершина. Определите вид сечения.
3. В тетраэдр ABCD вписана правильная треугольная призма с равными ребрами таким образом, что вершины одного ее основания находятся на боковых ребрах AD , BD , CD , а другого – в плоскости ABC . Ребро тетраэдра равно a . Найдите ребро призмы.
4. В тетраэдре ABCD проведите сечение плоскостью, проходящей через точку M – середину высоты DO тетраэдра, параллельно плоскости грани ADC . Определите вид сечения.
1. Нарисуйте: а) развертку куба; б) многогранник, двойственный тетраэдру.
2. Постройте сечение октаэдра плоскостью, проходящей через два его параллельных ребра. Определите вид сечения.
3. В октаэдр вписан куб таким образом, что его вершины находятся на ребрах октаэдра. Ребро октаэдра равно a . Найдите ребро куба.
4. В тетраэдре ABCD проведите сечение плоскостью, проходящей через точку M , принадлежащую грани ABC параллельно плоскости грани BCD . Определите вид сечения.
28*. Полуправильные многогранники
1. Найдите число вершин (В), ребер (Р) и граней (Г) усеченного гексаэдра.
2. Как можно получить 5-угольную антипризму?
3. Нарисуйте многогранник, двойственный правильной 6-угольной призме.
4. Правильный треугольник ABC и другой треугольник ADC имеют общую сторону AC и расположены в разных плоскостях, угол между которыми равен 30 0 . Вершина D ортогонально проектируется на плоскость треугольника ABC в его центр. Высота правильного треугольника равна h . Найдите сторону AD треугольника ADC .
1. Найдите число вершин (В), ребер (Р) и граней (Г) усеченного октаэдра.
2. Как можно получить 8-угольную антипризму?
3. Нарисуйте многогранник, двойственный 6-угольной антипризме.
4. Квадрат ABCD и треугольник ABE имеют общую сторону AB и расположены в разных плоскостях, угол между которыми равен 45 0 . Вершина E треугольника ортогонально проектируется на плоскость квадрата в его центр O . Высота EH треугольника равна h . Найдите площадь ортогональной проекции треугольника на плоскость квадрата и ортогональную проекцию отрезка OE на плоскость треугольника.
29*. Звездчатые многогранники
1. Как получить звезду Кеплера из октаэдра?
2. Найдите число вершин (В), ребер (Р) и граней (Г) малого звездчатого додекаэдра.
3. Каким образом из куба получается усеченный куб? Чему равно его ребро, если ребро куба равно a ?
4. Докажите, что если плоскость пересекает треугольную пирамиду и параллельна двум ее скрещивающимся ребрам, то в сечении будет параллелограмм.
1. Как получить звезду Кеплера из гексаэдра?
2. Найдите число вершин (В), ребер (Р) и граней (Г) большого додекаэдра.
3. Каким образом из куба получается кубооктаэдр? Чему равно его ребро, если ребро куба равно a ?
4. Докажите, что правильный тетраэдр можно пересечь плоскостью таким образом, чтобы в сечении получился квадрат.
30*. Кристаллы – природные многогранники
1. Нарисуйте кристалл горного хрусталя.
2. Нарисуйте ромбододекаэдр. Чему равно число его вершин, ребер и граней.
3. Найдите сумму всех плоских углов кристалла исландского шпата.
4. Найдите сумму площадей всех граней кристалла алмаза (в виде кубооктаэдра), если его ребро равно a .
1. Нарисуйте кристалл исландского шпата.
2. Нарисуйте ромбододекаэдр. Определите число его плоских углов, двугранных углов; многогранных углов и их тип.
3. Найдите сумму всех плоских углов кристалла граната.
4. Найдите сумму площадей всех граней кристалла алмаза (в виде усеченного октаэдра), если его ребро равно a .
31. Сфера и шар. Взаимное расположение сферы и плоскости
1. Шар, радиус которого равен 10 см, пересечен плоскостью, находящейся на расстоянии 9 см от центра. Найдите площадь сечения.
2. Сечения шара радиуса R двумя параллельными плоскостями имеют радиусы r 1 и r 2 . Найдите расстояние между этими плоскостями, если они расположены по разные стороны от центра.
3. Стороны треугольника касаются сферы. Найдите расстояние от центра сферы до плоскости треугольника, если радиус сферы равен 5 см, а стороны треугольника равны 12 см, 10 см, 10 см.
4. Каждая сторона ромба касается сферы радиуса 10 см. Плоскость ромба удалена от центра сферы на 8 см. Найдите площадь ромба, если его сторона равна 12,5 см.
1. Через середину радиуса шара проведена перпендикулярно к нему плоскость. Как относится площадь большого круга данного шара к площади получившегося сечения?
2. Сечения шара радиуса R двумя параллельными плоскостями имеют радиусы r 1 и r 2 . Найдите расстояние между этими плоскостями, если они расположены по одну сторону от центра.
3. Стороны ромба касаются сферы радиуса 13 см. Найдите расстояние от плоскости ромба до центра сферы, если диагонали ромба равны 30 см и 40 см.
4. Через конец радиуса шара проведена плоскость, составляющая с ним 30 0 . Найдите площадь сечения шара этой плоскостью, если радиус шара равен 6 см.
32. Многогранники, вписанные в сферу
1. Перечислите свойства, которым должна удовлетворять призма, чтобы около нее можно было описать сферу.
2. На рисунке 14 изображена треугольная пирамида ABCD , у которой ребро DB перпендикулярно плоскости ABC и угол ACB равен 90 0 . Найдите центр сферы, описанной около данной пирамиды.
3. В правильной четырехугольной пирамиде SABCD сторона основания ABCD равна 4 см, двугранный угол при основании 45 0 . Найдите радиус описанной сферы. Где будет находиться ее центр?
4. Радиус сферы, описанной около правильной четырехугольной призмы, равен R . Найдите высоту этой призмы, зная, что ее диагональ образует с боковой гранью угол a.
1. Перечислите свойства, которым должна удовлетворять пирамида, чтобы около нее можно было описать сферу.
2. На рисунке 15 изображена пирамида ABCD , у которой углы ADB , ADC и BDC прямые. Найдите центр сферы, описанной около данной пирамиды.
3. В правильной треугольной пирамиде SABC центр описанной сферы делит высоту на части, равные 6 см и 3 см. Найдите сторону основания ABC пирамиды.
4. В правильной 4-угольной призме диагональ основания и диагональ боковой грани равны соответственно 16 см и 14 см. Найдите радиус описанной сферы.
33. Многогранники, описанные около сферы
1. Можно ли вписать сферу в пирамиду, у которой равны двугранные углы при основании? Ответ поясните.
2. Около сферы описана прямая призма, основанием которой является ромб с диагоналями 6 см и 8 см. Найдите площадь основания и высоту призмы.
3. Сторона основания правильной четырехугольной пирамиды равна a , двугранный угол при основании равен 60 0 . Найдите радиус вписанного шара.
4. Стороны оснований правильной 4-угольной усеченной пирамиды равны 1 см и 7 см. Боковое ребро наклонено к основанию под углом 45 0 . Найдите радиус описанного шара.
1. Каким свойством должна обладать прямая треугольная призма, чтобы в нее можно было вписать сферу?
2. В основании пирамиды лежит равнобедренный треугольник, каждый из равных углов которого равен a и основание которого равно a . Боковые грани пирамиды наклонены к плоскости основания под углом b. Найдите радиус сферы, вписанной в эту пирамиду.
3. Найдите радиус шара, вписанного в правильную пирамиду, у которой высота равна h , а двугранный угол при основании равен 45 0 .
4. В правильной треугольной усеченной пирамиде высота равна 17 см, радиусы окружностей, описанных около оснований, равны 5 см и 12 см. Найдите радиус описанного шара.
34. Цилиндр. Конус
1. В цилиндре, радиус основания которого равен 4 см и высота 6 см, проведено сечение, параллельное оси. Расстояние между диагональю сечения и осью цилиндра равно 2 см. Найдите площадь сечения.
2. Через вершину конуса проведено сечение под углом 60 0 к его основанию. Найдите расстояние от центра основания конуса до плоскости сечения, если высота конуса равна 12 см.
3. Точка M принадлежит высоте конуса. Точка N принадлежит плоскости основания конуса, но находится вне этого основания. Постройте точку пересечения прямой MN с поверхностью конуса.
4. Диагонали осевого сечения усеченного конуса перпендикулярны, высота равна 2 см. Найдите площадь сечения усеченного конуса, проведенного через середину высоты параллельно основаниям.
1. Высота цилиндра равна 15 см, радиус основания 10 см. Дан отрезок, концы которого принадлежат окружностям обоих оснований и длина которого равна 3 
2. Через вершину конуса проведено сечение под углом 30 0 к его высоте. Найдите площадь сечения, если высота конуса равна 3 
3. В конусе задано осевое сечение. Точки K и L принадлежат двум образующим конуса, не лежащим в данном сечении. Постройте точку пересечения прямой KL с плоскостью данного осевого сечения.
4. Радиусы оснований усеченного конуса относятся как 1:3, образующая составляет с плоскостью основания угол 45 0 , высота равна h . Найдите площади оснований.
35. Поворот. Фигуры вращения
1. Нарисуйте фигуру, которая получается при вращении квадрата ABCD вокруг прямой a , проходящей через вершину B и перпендикулярной диагонали BD .
2. Нарисуйте фигуру, которая получается вращением круга вокруг касательной.
3. Кривая задана уравнением y = sin x , 0 

4. Плоскость проходит через ось цилиндра, причем площадь осевого сечения цилиндра относится к площади его основания как 4: p. Найдите угол между диагоналями осевого сечения.
1. Нарисуйте фигуру, которая получается при вращении ромба ABCD вокруг прямой a , проходящей через вершину C и перпендикулярной диагонали AC .
2. Нарисуйте фигуру, которая получается вращением круга вокруг хорды, не являющейся диаметром.
3. Кривая задана уравнением y = 


4. Высота конуса равна 20 см, угол между нею и образующей 60 0 . Найдите площадь сечения, проведенного через две взаимно перпендикулярные образующие конуса.
36. Вписанные и описанные цилиндры
1. В сферу радиуса 10 см вписан цилиндр, диагональ осевого сечения которого наклонена к плоскости основания под углом 30 0 . Найдите высоту цилиндра и радиус его основания.
2. Найдите радиус основания цилиндра, описанного около сферы радиуса R .
3. В равносторонний цилиндр (высота равна диаметру основания), радиус основания которого равен r , вписана правильная треугольная призма. Найдите площадь сечения призмы, проходящего через ось цилиндра и боковое ребро призмы.
4. Около равностороннего цилиндра, радиус основания которого равен r , описана правильная четырехугольная призма. Найдите площади ее граней.
1. В сферу вписан цилиндр, образующая которого равна 8 см и диагональ осевого сечения наклонена к плоскости основания под углом 60 0 . Найдите радиусы сферы и основания цилиндра.
2. Найдите образующую цилиндра, описанного около сферы радиуса R .
3. В равносторонний цилиндр (высота равна диаметру основания), радиус основания которого равен r , вписана правильная четырехугольная призма. Найдите площадь сечения призмы, проходящего через ось цилиндра и боковое ребро призмы.
4. Около равностороннего цилиндра, радиус основания которого равен r , описана правильная треугольная призма. Найдите площади ее граней.
37*. Сечения цилиндра плоскостью. Эллипс
1. Изобразите цилиндр и эллипс, являющийся пересечением боковой поверхности цилиндра плоскостью, образующей с основанием цилиндра угол 45 0 .
2. Боковая поверхность цилиндра пересечена плоскостью, образующей с осью цилиндра угол 30 0 . Найдите большую ось эллипса, получившегося в сечении, если радиус основания цилиндра равен R .
3. Плоскость пересекает боковую поверхность цилиндра и образует с плоскостью основания угол 30 0 . Найдите расстояние между фокусами эллипса, получившегося в сечении, если радиус основания цилиндра равен 3 см.
4. Цилиндр, радиус основания которого равен R , пересечен плоскостью, образующей с основанием цилиндра угол 45 0 . Найдите сумму расстояний от точек эллипса, получившегося в сечении, до фокусов.
1. Изобразите цилиндр и эллипс, являющийся пересечением боковой поверхности цилиндра плоскостью, образующей с основанием цилиндра угол 60 0 .
2. Под каким углом к плоскости основания цилиндра нужно провести плоскость, чтобы в сечении боковой поверхности получить эллипс, у которого большая ось в два раза больше малой?
3. Плоскость пересекает боковую поверхность цилиндра и образует с плоскостью основания угол 45 0 . Найдите расстояние между фокусами эллипса, получившегося в сечении, если радиус основания цилиндра равен 2 см.
4. Цилиндр, радиус основания которого равен R , пересечен плоскостью, образующей с основанием цилиндра угол 30 0 . Найдите сумму расстояний от точек эллипса, получившего в сечении, до фокусов.
38. Вписанные и описанные конусы
1. В сферу радиуса 4 см вписан конус. Найдите высоту этого конуса и радиус его основания, если угол при вершине осевого сечения равен 60 0 .
2. Радиус основания конуса равен r , образующая наклонена к плоскости основания под углом 60 0 . Найдите радиус вписанной в конус сферы.
3. Можно ли вписать в конус 4-угольную пирамиду, у которой углы основания последовательно относятся как: а) 1:5:9:7; б) 4:2:5:7?
4. Основанием пирамиды является равнобедренная трапеция с основаниями 8 см и 18 см; двугранные углы при основании пирамиды равны. В пирамиду вписан конус. Найдите радиус основания конуса и его высоту, если меньшее боковое ребро пирамиды составляет с меньшей стороной трапеции угол 60 0 .
1. В конусе образующая равна 15 см и составляет с основанием угол 60 0 . Найдите радиус описанной сферы.
2. В конус вписана сфера, радиус которой равен R . Найдите радиус основания конуса, если угол при вершине осевого сечения равен 60 0 .
3. Можно ли описать около конуса 4-угольную пирамиду, у которой стороны основания последовательно относятся как: а) 5:6:8:7; б) 3:10:15:7?
4. Основанием пирамиды является прямоугольный треугольник; боковые ребра равны между собой, а боковые грани, проходящие через катеты, составляют с основанием углы 30 0 и 60 0 . Около пирамиды описан конус таким образом, что у них общая высота. Найдите радиус основания конуса, если высота пирамиды равна h .
39*. Конические сечения
1. Образующая конуса наклонена к плоскости его основания под углом 60 0 . Радиус основания конуса равен R . Через центр основания проведена плоскость под углом 60 0 к плоскости основания. Найдите радиус сферы, вписанной в коническую поверхность и касающуюся этой плоскости.
2. Изобразите конус и плоскость, пересекающую коническую поверхность по эллипсу.
3. Угол при вершине осевого сечения конуса равен 90 0 . Под каким углом к плоскости основания конуса нужно провести плоскость, чтобы в сечении конической поверхности получить: а) эллипс; б) параболу; в) гиперболу?
4. Угол между осью конуса и его образующей равен 45 0 . Через точку образующей, отстоящую от вершины конуса на расстояние a , проведена плоскость, перпендикулярная этой образующей. Найдите расстояние между фокусом и директрисой параболы, получающейся в сечении конической поверхности этой плоскостью.
1. Угол при вершине осевого сечения конуса равен 90 0 . Через точку образующей, отстоящей от вершины конуса на расстояние a , проведена плоскость, перпендикулярная этой образующей. Найдите радиус сферы, вписанной в коническую поверхность, касающуюся этой плоскости.
2. Изобразите конус и плоскость, пересекающую коническую поверхность по параболе.
3. Образующая конуса наклонена к плоскости его основания под углом 60 0 . Под каким углом к плоскости основания нужно провести плоскость, чтобы в сечении конической поверхности получить: а) эллипс; б) параболу; в) гиперболу?
4. Угол при вершине осевого сечения конуса равен 30 0 . Через точку образующей, отстоящей от вершины на расстояние b , проведена плоскость, перпендикулярная этой образующей. Найдите большую ось эллипса, получившегося в сечении конической поверхности этой плоскостью.
40. Симметрия пространственных фигур
1. Для двух точек пространства найдите точку, относительно которой они центрально симметричны.
2. Постройте прямую, зеркально-симметричную данной прямой относительно данной плоскости a. Рассмотрите различные случаи.
3. Докажите, что при осевой симметрии плоскость, перпендикулярная оси, переходит в себя.
4. Найдите элементы симметрии правильной треугольной призмы.
1. Для двух точек пространства найдите прямую, относительно которой они симметричны.
2. Постройте плоскость, центрально-симметричную данной плоскости относительно точки O . Рассмотрите различные случаи.
3. Докажите, что при осевой симметрии прямые, перпендикулярные оси, переходят в прямые, также перпендикулярные оси.
4. Найдите элементы симметрии правильной 6-ной пирамиды.
1. Докажите, что композиция двух движений (последовательное их выполнение) является движением.
2. Найдите движения, которые переводят вершину A куба A … D 1 в вершину C 1 .
3. Найдите движения, которые переводят вершину A правильного тетраэдра ABCD в вершину C .
4. Каким движением является композиция (последовательное выполнение) двух осевых симметрий с параллельными осями?
1. Докажите, что преобразование, обратное движению, тоже является движением.
2. Найдите движения, которые переводят вершину B 1 куба A … D 1 в вершину D .
3. Найдите движения, которые переводят вершину D правильного тетраэдра ABCD в вершину B .
4. Каким движением является композиция (последовательное выполнение) двух центральных симметрий?
42*. Ориентация поверхности. Лист Мебиуса
1. Сколько сторон имеет поверхность: а) пирамиды; б) призмы; в) дважды перекрученной ленты Мебиуса?
2. Изобразите лист Мебиуса.
3. Лист Мебиуса получен из прямоугольника со сторонами a , b ( a b ) склеиванием сторон длины a . Какова площадь поверхности листа Мебиуса?
4. Можно ли одностороннюю поверхность склеить из шестиугольника?
1. Сколько сторон имеет поверхность: а) конуса; б) цилиндра; в) листа Мебиуса?
2. Изобразите дважды перекрученную ленту Мебиуса.
3. Лист Мебиуса получен из прямоугольника со сторонами a , b ( a b ) склеиванием сторон длины a . Какова длина края листа Мебиуса?
4. Можно ли одностороннюю поверхность склеить из восьмиугольника?
43. Объем фигур в пространстве. Объем цилиндра
1. Осевое сечение прямого кругового цилиндра — квадрат со стороной 3 см. Найдите объем цилиндра.
2. От куба A … D 1 , ребро которого равно 1, отсечены 4 треугольные призмы плоскостями, которые проходят через середины смежных сторон грани ABCD , параллельно ребру AA 1 . Найдите объем оставшейся части куба.
3. Прямая треугольная призма пересечена плоскостью, которая проходит через боковое ребро и делит площадь противолежащей ему боковой грани в отношении m : n . В каком отношении делится объем призмы?
4. Основанием прямого параллелепипеда является ромб, диагонали которого относятся как 5:2. Зная, что диагонали параллелепипеда равны 17 дм и 10 дм, найдите объем параллелепипеда.
1. Диагональ осевого сечения цилиндра равна 2 см и наклонена к плоскости основания под углом 60 0 . Найдите объем цилиндра.
2. Объем правильной шестиугольной призмы равен V . Определите объем призмы, вершинами которой являются середины сторон оснований данной призмы.
3. В каком отношении делится объем прямой треугольной призмы плоскостью, проходящей через средние линии оснований.
4. Основанием прямого параллелепипеда является ромб, диагонали которого равны 1 дм и 7 дм. Зная, что диагонали параллелепипеда относятся как 13:17, найдите объем параллелепипеда.
44. Принцип Кавальери
1. Верно ли, что два конуса, имеющие равные основания и высоты, равновелики?
1. Найдите объем наклонной призмы, площадь основания которой равна S , а боковое ребро b наклонено к плоскости основания под углом 60 0 .
3. В наклонном параллелепипеде две боковые грани имеют площади S 1 и S 2 , их общее ребро равно a , и они образуют между собой двугранный угол 150 0 . Найдите объем параллелепипеда.
4. В наклонной треугольной призме площадь одной из боковых граней равна Q , а расстояние от нее до противоположного ребра равно d . Найдите объем призмы.
1. Верно ли, что две пирамиды, имеющие равновеликие основания и равные высоты, равновелики?
2. Найдите объем наклонного цилиндра, радиус основания которого равен R , а боковое ребро b наклонено к плоскости основания под углом 45 0 .
3. В наклонном параллелепипеде основание и боковая грань являются прямоугольниками и их площади равны соответственно 20 см 2 и 24 см 2 . Угол между их плоскостями равен 30 0 . Еще одна грань параллелепипеда имеет площадь 15 см 2 . Найдите объем параллелепипеда.
4. В наклонной треугольной призме две боковые грани перпендикулярны и имеют общее ребро, равное a . Площади этих граней равны S 1 и S 2 . Найдите объем призмы.
45. Объем пирамиды
1. Пирамида, объем которой равен V , а в основании лежит прямоугольник, пересечена четырьмя плоскостями, каждая из которых проходит через вершину пирамиды и середины смежных сторон основания. Найдите объем оставшейся части пирамиды.
2. Основанием пирамиды является равносторонний треугольник со стороной, равной 1. Две ее боковые грани перпендикулярны плоскости основания, а третья образует с основанием угол 60 0 . Найдите объем пирамиды.
3. В основании прирамиды лежит прямоугольный треугольник, один из катетов которого равен 3 см, а прилежащий к нему острый угол равен 30 0 . Все боковые ребра пирамиды наклонены к плоскости основания под углом 60 0 . Найдите объем пирамиды.
4. Центры граней куба, ребро которого равно 2 a , служат вершинами октаэдра. Найдите его объем.
1. Найдите объем правильной четырехугольной пирамиды, если ее диагональным сечением является правильный треугольник со стороной, равной 1.
2. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60 0 . Высота пирамиды равна 3 см. Найдите объем пирамиды.
3. Боковые грани пирамиды, в основании которой лежит ромб, наклонены к плоскости основания под углом 30 0 . Диагонали ромба равны 10 см и 24 см. Найдите объем пирамиды.
4. В куб с ребром, равным a , вписан правильный тетраэдр таким образом, что его вершины совпадают с четырьмя вершинами куба. Найдите объем тетраэдра.
46. Объем конуса
Вариант 1
1. Диаметр основания конуса равен 12 см, а угол при вершине осевого сечения равен 90 0 . Найдите объем конуса.
2. Два конуса имеют общую высоту и параллельные основания. Найдите объем их общей части, если объем каждого конуса равен V .
3. В конус, объем которого равен V , вписан цилиндр. Найдите объем цилиндра, если отношение диаметров оснований конуса и цилиндра равно 10:9.
4. Каждое ребро правильной 4-угольной пирамиды равно a . Плоскость, параллельная плоскости основания пирамиды, отсекает от нее усеченную пирамиду. Найдите объем усеченной пирамиды, если сторона сечения равна b .
Вариант 2
1. Осевым сечением конуса служит равнобедренный прямоугольный треугольник площади 9 см 2 . Найдите объем конуса.
2. В конус вписан другой конус таким образом, что центр основания вписанного конуса делит высоту данного конуса в отношении 3:2, считая от вершины конуса, а вершина вписанного конуса находится в центре основания данного конуса. Найдите отношение объемов данного и вписанного конусов.
3. Докажите, что если два равных конуса имеют общую высоту и параллельные плоскости оснований, то объем их общей части составляет 
4. Радиусы оснований усеченного конуса равны 3 см и 5 см. Найдите отношение объемов частей усеченного конуса, на которые он делится средним сечением.
47. Объем шара и его частей
Вариант 1
1. Найдите отношение объема шара к объему вписанного в него куба.
2. Найдите отношение объема шара к объему описанного около него октаэдра.
3. В шаре проведена плоскость, перпендикулярная диаметру и делящая его на части, равные 3 см и 9 см. Найдите объемы частей шара.
4. Радиус шарового сектора R , угол в осевом сечении 120 0 . Найдите объем шарового сектора.
Вариант 2
1. Найдите отношение объема шара к объему вписанного в него октаэдра.
2. Найдите отношение объема шара к объему описанного около него куба.
3. В шаре радиуса 13 см проведены по разные стороны от центра два равных параллельных сечения радиуса 5 см. Найдите объем полученного шарового слоя.
4. Найдите объем шарового сектора, если радиус окружности его основания равен 60 см, а радиус шара 75 см.
48. Площадь поверхности
Вариант 1
1. Плоскость, проходящая через сторону основания правильной треугольной призмы и середину противолежащего ребра, образует с основанием угол 45 0 , а сторона основания равна a . Найдите площадь боковой и полной поверхности призмы.
2. Основанием пирамиды является квадрат, сторона которого равна a . Две грани пирамиды перпендикулярны основанию, а остальные две боковые грани наклонены к нему по углом 60 0 . Найдите площадь боковой поверхности пирамиды.
3. В правильной четырехугольной призме сторона основания равна b ; сечение, проведенное через противоположные стороны оснований, составляет с плоскостью основания угол j. Найдите площадь боковой поверхности цилиндра, описанного около данной призмы.
4. Угол при вершине осевого сечения конуса равен 60 0 ; площадь большого круга, вписанного в этот конус шара, равна Q . Найдите площадь полной поверхности конуса.
Вариант 2
1. В правильной 4-угольной призме сторона основания равна a . Плоскость, проведенная через противоположные стороны оснований, составляет с одним из них угол 60 0 . Найдите площадь боковой и полной поверхности призмы.
2. Две боковые грани треугольной пирамиды перпендикулярны ее основанию; высота пирамиды равна h ; плоские углы при вершине равны 60 0 , 60 0 и 90 0 . Найдите площадь боковой поверхности пирамиды.
3. В правильной треугольной призме боковое ребро равно b ; отрезок, соединяющий середину бокового ребра с центром основания, составляет с основанием угол j. Найдите площадь боковой поверхности цилиндра, вписанного в данную призму.
4. В конусе образующая составляет с основанием угол 60 0 ; площадь большого круга описанного шара равна Q . Найдите площадь полной поверхности конуса.
49. Площадь поверхности шара и его частей
Вариант 1
1. Докажите, что площадь полной поверхности равностороннего конуса (осевое сечение – равносторонний треугольник) равна площади поверхности шара, имеющего диаметром высоту конуса.
2. Найдите площадь поверхности шара, вписанного в равносторонний цилиндр (осевое сечение – квадрат), диагональ осевого сечения которого равна a .
3. Радиусы оснований шарового пояса равны 10 см и 12 см, а его высота равна 11 см. Найдите площадь поверхности шарового пояса.
4. Радиус шарового сегмента равен R , дуга осевого сечения составляет 90 0 . Найдите площадь полной поверхности сегмента.
1. Докажите, что если равносторонний конус (осевое сечение – равносторонний треугольник) и полушар имеют общее основание, то площадь боковой поверхности конуса равна площади поверхности полушара.
2. Найдите отношение площадей поверхностей двух шаров, один из которых вписан, а второй описан около равностороннего цилиндра (осевое сечение – квадрат).
3. Радиус шара равен 25 см. Найдите площади частей, на которые делится поверхности шара сечением, площадь которого равна 49p см 2 .
4. Высота шарового сегмента равна h , дуга осевого сечения равна 120 0 . Найдите площадь полной поверхности сегмента.
50. Прямоугольная система координат в пространстве
1. Постройте по координатам точки: A (1,2,3); B (-2,0,3); C (0,0,-4); D (3,-1,0).
2. Среди данных точек K (-6,0,0), L (10,-5,0), M (0,6,0), N (7,-8,0), P (0,0,-20), Q (0,11,-2) найдите те, которые принадлежат: а) оси Oy ; б) оси Oz ; в) плоскости Oxy ; г) плоскости Oyz .
3. Найдите координаты оснований перпендикуляров, опущенных из данных точек E (6,-2,8) и F (-3,2,-5) на: а) ось Ox ; б) плоскость Oxz .
4. Найдите координаты середины отрезка GH , если G (2,-3,5), H (4,1,-3).
5. Найдите координаты точек, симметричных точкам U (8,0,6), V (20,-14,0) относительно: а) плоскости Oyz ; б) оси Ox .
1. 1. Постройте по координатам точки: E (-1,2,0); F (1,0,-4); G (2,3,-1); H (0,-2,0).
2. Среди точек A (0,-1,0), B (0,1,-3), C (4,0,0), D (0,0,-5), E (-1,0,7), F (0,10,10) найдите те, которые принадлежат: а) оси Ox ; б) оси Oy ; в) плоскости Oyz ; г) плоскости Oxz .
3. Найдите координаты оснований перпендикуляров, опущенных из точек M (9,-1,-6) и N (-12,5,8) на: а) ось Oz ; б) плоскость Oxy .
4. Найдите координаты середины отрезка GH , если G (3,-2,4), H (5,2,-6).
5. Найдите координаты точек, симметричных точкам P (0,0,5), V (0,-1,-2) относительно: а) плоскости Oxy ; б) оси Oy .
51. Расстояние между точками в пространстве
1. Определите, являются ли точки A (2,3,4), B (1,2,3), C (3,4,5) вершинами треугольника.
2. Найдите координаты точки, принадлежащей оси Oz и одинаково удаленной от точек M (-1,-2,0) и N (3,0,4).
3. Запишите уравнение сферы с центром в точке C (-2,0,3) и: а) радиусом 
4. Найдите координаты центра и радиус сферы, заданной уравнением x 2 + 8 y + y 2 + z 2 – 6 x =0.
5. Сфера x 2 + y 2 + z 2 +4 x – 2 y =0 пересечена плоскостью Oyz . Найдите координаты центра и радиус окружности, лежащей в сечении.
1. Определите, являются ли точки E (-4,-5,-6), F (-1,-2,-3), G (-2,-3,-4) вершинами треугольника.
2. Найдите координаты точки, принадлежащей оси Oy и одинаково удаленной от точек K (1,3,0) и L (4,-1,3).
3. Запишите уравнение сферы с центром в точке C (0,-5,6) и: а) радиусом 10; б) проходящей через точку H (2,-3,5).
4. Найдите координаты центра и радиус сферы, заданной уравнением x 2 + y 2 + z 2 – 8 z — 20 =0.
5. Сфера x 2 + y 2 + z 2 +2 x – 6 z =0 пересечена плоскостью Oxy . Найдите координаты центра и радиус окружности, лежащей в сечении.
52. Координаты вектора
1. Найдите координаты вектора: а) 2 







2. Найдите длину вектора: а) 





3. Найдите координаты точки C , если: а) 


4. Найдите числа x , y , z , чтобы выполнялось равенство 





1. Найдите координаты вектора: а) 3 







2. Найдите длину вектора: а) 





3. Найдите координаты точки E , если: а) 

4. Найдите числа u , v , w , чтобы выполнялось равенство 





53. Скалярное произведение векторов
1. Определите знак скалярного произведения векторов 


2. Угол между векторами 





3. Докажите равенство: а) 



4. В правильном тетраэдре ABCD с ребром, равным 1, найдите скалярное произведение: а) 


1. Определите, в каком промежутке находится угол 





2. Угол между векторами 





3. Докажите равенство: а) 


4. В правильном тетраэдре ABCD с ребром, равным a , найдите скалярное произведение: а) 


54. Уравнение плоскости в пространстве
1. Напишите уравнение плоскости, проходящей через точку H (-3,0,7) и перпендикулярную вектору с координатами (1,-1,3).
2. Найдите координаты точки пересечения плоскости 2 x – y + 3 z – 1 = 0 с осью: а) абсцисс; б) ординат.
3. Напишите уравнение плоскости, если она проходит через точку B (3,-2,2) и: а) параллельна плоскости Oyz ; б) перпендикулярна оси Ox .
4. Напишите уравнение плоскости, которая проходит через точку M (5,-1,3) и перпендикулярна вектору 
1. Напишите уравнение плоскости, проходящей через точку P (5,-1,0) и перпендикулярную вектору с координатами (0,-6,10).
2. Найдите координаты точки пересечения плоскости x + 4 y — 6 z – 7 = 0 с осью: а) ординат; б) аппликат.
3. Напишите уравнение плоскости, если она проходит через точку C (2,-4,-3) и: а) параллельна плоскости Oxz ; б) перпендикулярна оси Oy .
4. Напишите уравнение плоскости, которая проходит через точку E и перпендикулярна вектору 
55*. Уравнение прямой в пространстве
1. Найдите значение d , при котором прямая
пересекает ось Oz .
2. Найдите условия, которым должны удовлетворять коэффициенты в уравнениях прямой
для того, чтобы прямая: а) была параллельна оси Ox ; б) лежала в плоскости Oxz ; в) пересекала ось Oy .
3. Найдите координаты точек пересечения прямой
с координатными плоскостями.
4. Запишите параметрические уравнения прямой
1. Найдите значения b и d , при которых прямая
пересекает плоскость Oxy .
2. Найдите условия, которым должны удовлетворять коэффициенты в уравнениях прямой
для того, чтобы прямая: а) совпадала с осью Oz ; б) была параллельна плоскости Oyz ; в) проходила через начало координат.
3. Найдите координаты точек пересечения прямой
с координатными плоскостями.
4. Запишите параметрические уравнения прямой
56. Аналитическое задание пространственных фигур
1. Выясните, какую геометрическую фигуру задает уравнение: а) x 2 + y 2 + z 2 = 1; б) x 2 = 1; в) xyz = 0.
2. Выясните, какую геометрическую фигуру задает система:
а) 
3. Даны точки A (2,5,12), B (1,0,0), C (-1,-5,4) и плоскости 

4. Дана плоскость 3 x – y +4 z +1 = 0. Лежат ли по одну и ту же сторону от нее точки: а) O (0,0,0) и D (2,1,0); б) E (1,2,1) и F (5,15,-1)?
1. Выясните, какую геометрическую фигуру задает уравнение: а) x 2 + y 2 +(z+1) 2 = 1; б) x 2 – y 2 = 0; в) x 2 = 0.
2. Выясните, какую геометрическую фигуру задает система:
а) 
3. Даны точки E (-14,22,0), F (1,-5,12), G (0,0,5) и плоскости 

4. Дана плоскость 3 x – y +4 z +1 = 0. Лежат ли по одну и ту же сторону от нее точки: а) A (-1,2,-5) и B (-15,1,0); б) K (1, 
57*. Многогранники в задачах оптимизации
1. Вершины тетраэдра имеют следующие координаты: O (0,0,0), A (1,1,0), B (0,2,0), C (1,5,7). Запишите неравенства, характеризующие внутреннюю область данного тетраэдра.
2. Найдите область, определяемую следующей системой неравенств:
а) 
3. Запишите систему неравенств, определяющую внутреннюю область прямой треугольной призмы OABO 1 A 1 B 1 , если O (0,0,0), A (0,2,0), B (0,0,2), O 1 (5,0,0). Изобразите ее и найдите ее объем.
4. Найдите наибольшее и наименьшее значения линейной функции u = x + y – 2 z + 1 на треугольной призме из предыдущей задачи.
1. Даны вершины тетраэдра A (-1,1,0), B (-2,2,0), C (-2,0,0), D (-1,5,7). Какие из точек M (2,3,-1), N (- 





2. Найдите область, определяемую следующей системой неравенств: а) 
3. Запишите систему неравенств, определяющих внутреннюю область тетраэдра OABC , если O (0,0,0), A (5,0,0), B (0,3,0), C (0,0,6). Изобразите ее и найдите ее объем.
4. Найдите наибольшее и наименьшее значения линейной функции u = x – y + z – 1 на тетраэдре из предыдущей задачи.
58*. Полярные координаты на плоскости
1. Изобразите в полярной системе координат точки A (2, 







2. Запишите декартовы координаты точек G (2, 




3. Найдите полярные координаты вершин и точки пересечения диагоналей единичного квадрата, приняв за начало координат одну из его вершин, а за полярную ось – сторону, которая проходит через выбранную вершину.
4. Найдите полярные координаты точек, симметричных точкам M (1, 





1. Изобразите в полярной системе координат точки A (3, 







2. Запишите полярные координаты точек K (0,6), L (-2,0), M (-1,1), N ( 
3. Найдите полярные координаты вершин правильного шестиугольника, сторона которого равна 1, приняв за начало координат одну из его вершин, а за полярную ось – сторону, которая проходит через выбранную вершину.
4. Найдите полярные координаты точек, симметричных точкам G (2, 




59*. Сферические координаты в пространстве
1. Найдите декартовы координаты следующих точек пространства, заданных сферическими координатами: (1,45 0 ,60 0 ), (2,30 0 ,90 0 ), (1,90 0 , 20 0 ).
2. Найдите сферические координаты следующих точек пространства, заданных декартовыми координатами: A (1,1, 
3. Найдите геометрическое место точек пространства, сферические координаты которых удовлетворяют условиям: а) y = 45 0 ; б) j= 60 0 .
4. Какая фигура в пространстве задается неравенствами: а) r 


1. Найдите декартовы координаты следующих точек пространства, заданных сферическими координатами: (1,-45 0 ,60 0 ), (2,30 0 ,-90 0 ), (3,-90 0 , 50 0 ).
2. Найдите сферические координаты следующих точек пространства, заданных декартовыми координатами: A (2,2 
3. Найдите геометрическое место точек пространства, сферические координаты которых удовлетворяют условиям: а) y= 30 0 ; б) j = 90 0 .
4. Какая фигура в пространстве задается неравенствами: а) r 




60*. Использование компьютерной программы «Математика» для изображения пространственных фигур
1. Получите изображение тетраэдра.
2. Произведите операцию усечения тетраэдра и получите октаэдр.
3. Как из октаэдра получить звезду Кеплера?
4. Получите изображение поверхности z = xy .
1. Получите изображение куба.
2. Произведите операцию усечения куба и получите кубооктаэдр.
3. Как из куба получить ромбододекаэдр?
4. Получите изображение поверхности z = cos x cos y .
Самостоятельная работа N 2
В1. 4. 6. В2. 3. 10. 4. 4.
В1. 2. а) В=8, Р=12, Г=6; б) В=14, Р=21, Г=9; в) В= n +1, Р=2 n , Г= n +1. 3. а) 5-угольная; б) 7-угольная; в) 3-угольная. 4. Три цвета. В2. 2. а) В=8, Р=12, Г=6; б) В=7, Р=12, Г=7; в) В=2 n , Р=3 n , Г= n +2. 3. а) 4-угольная; б) 7-угольная; в) 8-угольная. 4. Два цвета.
В1. 3. 3. 4. 3. В2. 3. 3. 4. 3.
В1. 3. Скрещиваются. В2. 3. Нет. 4. Нет.
В1. 3. Параллельны.
В1. 2. Верны утверждения 1), 3), 4). 4. Если AB || CD , то AC || BD ; если AB скрещивается с CD , то AC скрещивается с BD . В2. 2. Верно утверждение 3). 4. Если AB || CD , то AD и BC пересекаются; если AB и CD скрещиваются, то AD и BC скрещиваются.
В1. 2. 26. 3. а) 











В1. 1. 















В1. 1. Одна, если прямая, проходящая через них, параллельна направлению проектирования; две в противном случае. 2. Параллельность и равенство противоположных сторон; деление диагоналей пополам в точке пересечения. 3. Прямые скрещиваются и одна из них параллельна направлению проектирования. В2. 1. Одна, если все точки принадлежат одной прямой, параллельной направлению проектирования; две, если прямая, проходящая через какие-нибудь две из данных точек, параллельна направлению проектирования, а третья точка не принадлежит этой прямой; три в остальных случаях. 2. Параллельность и равенство противоположных сторон; деление диагоналей в точке пересечения пополам. 3. Прямая не параллельна направлению проектирования и точка принадлежит прямой или плоскость, проходящая через эту точку и прямую, параллельна направлению проектирования.
В1. 3. Грани куба не параллельны плоскости проектирования и направление проектирования параллельно диагонали BD . 4. S . В2. 3. Две грани параллельны плоскости проектирования и направление проектирования перпендикулярно ей. 4. Q /2.
В1. 1. а), б), г) 90 0 ; в) 45 0 . 2. а), б) 90 0 . 3. 45 0 . 4. 90 0 . В2. 1. а), в), г) 90 0 ; б) 45 0 . 2. а) 90 0 ; б) 30 0 . 3. cos 

В1. 1. 9 см. 3. 
В1. 2. cos 



В1. 1. 6 см. 2. а) 





В1. 1. 



Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Самостоятельная работа N 1
В1. 3. 

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Самостоятельная работа N 2
В1. 4. 

В1. 2. 14 см 2 . 3. По 6 прямым. В2. 2. 
В1. 1. а), б) В = 2 n , Р = 3 n , Г = n + 2. 3. 





В1. 4. 

В1. 1. б) Октаэдр. 2. Ромб. 3. 

В1. 1. В=24, Р=36, Г=14. 4. 


В1. 3. (  -1) a . В2. 3.
-1) a . В2. 3.  .
.
В1. 2. В=14, Р=24, Г=12. 3. 2160 0 . 4. 


В1. 1. 19p см 2 . 2. 

В1. 3. 3 см. 4. 2 R 
В1. 1. Да. 2. 24 см 2 , 4,8 см. 3. 


В1. 1. 24 



В1. 4. 90 0 . В2. 4. 800 см 2 .
В1. 1. 10 см, 5 




В1. 2. 4 R . 3. 2 


В1. 1. 6 см, 2 





В1. 1. R 








В1. 4. Одна ось симметрии третьего порядка; Три оси симметрии; Четыре плоскости симметрии. В2. Одна ось симметрии 6-го порядка; Шесть плоскостей симметрии.
В1. 4. Параллельным переносом. В2. 4. Параллельным переносом.
В1. 1. а), б), в) Две. 3. 2 ab . 4. Да. В2. 1. а), б) Две; в) одну. 3. 2 b . 4. Да.
В1. 1. 27p см 3 . 2. 


В1. 1. Да. 2. S 






В1. 1. 






В1. 1. 72 



В1. 1. 











В1. 1. 3 









В1. 2. 






В1. 2. а) M ; б) P ; в) K , L , M , N ; г) M , P , Q . 3. а) (6,0,0), (-3,0,0); б) (6,0,8), (-3,0,-5). 4. (3,-1,1). 5. а) (-8,0,6), (-20,-14,0); б) (8,0,-6), (20,14,0). В2. 2. а) C ; б) A ; в) A , B , D , F ; г) C , D , E . 3. а) (0,0,-6), (0,0,8); б) (9,-1,0), (-12,5,0). 4. (4,0,-1). 5. а) (0,0,-5), (0,-1,2); б) (0,0,-5), (0,-1,2).
В1. 1. Нет. 2. (0,0, 
В1. 1. а) (2,3,-4); б) (-5,0,10); в) (0,-1, 







В1. 1. а) 











В1. 1. x – y + 3 z – 18 = 0. 2. а) ( 


В1. 1. d = 3. 2. а) a 1 = a 2 = 0; б) a 1 : a 2 = c 1 : c 2 = d 1 : d 2 ; в) b 1 : b 2 = d 1 : d 2 . 3. (-1,7 



В1. 1. а) Сфера с центром в точке O (0,0,0) и радиусом 1; б) две параллельные плоскости; в) три координатные плоскости. 2. а) Прямоугольный параллелепипед; б) окружность. 3. Для 



В1. 1.
2. а) Внутренняя область тетраэдра с вершинами (0,0,0), (1,0,0). (0,1,0), (0,0,1); б) внутренняя область прямоугольного параллелепипеда с вершинами (5,5,0), (5,3,0), (7,3,0), (7,5,0), (5,5,10), (5,3,10), (7,3,10), (7,5,10).
3. 
В2. 1. Точки N и H . 2. а) Область между двумя параллельными плоскостями; б) внутренняя область прямой треугольной призмы с вершинами (0,0,0), (0,3,0). (0,0,3), (-2,0,0), (-2,3,0), (-2, 0,3).
3. 
В1. 2. G (1, 










































В1. 1. ( 










В1. 3. Применить операцию Stellate. В2. 3. Применить операцию Stellate.
Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Сколько пар равных векторов задаются вершинами треугольной призмы?
Видео:Линейные комбинации, span и базисные вектора | Сущность Линейной Алгебры, глава 2Скачать

Ваш ответ
Видео:Коллинеарность векторовСкачать

Похожие вопросы
- Все категории
- экономические 43,279
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,962
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
💡 Видео
Как разложить вектор по базису - bezbotvyСкачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Все типы 2 задание векторы ЕГЭ по математике профиль 2024Скачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Вектора. Что нужно знать про вектор, когда идешь на первый курс.Скачать

Образуют ли данные векторы базисСкачать

Решение задач на векторное и смешанное произведения векторовСкачать

Физика | Ликбез по векторамСкачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Векторы и действия над ними, проекция вектора на координатные оси. Практическая часть. 9 класс.Скачать
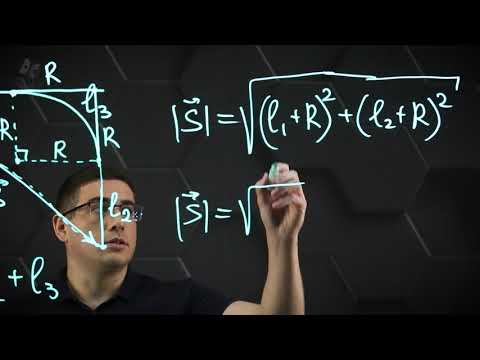
Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

























































 .
.
