Сформулируйте используя законы де моргана отрицания следующих утверждений четырехугольник

Видео:3.8 Де Морган правилаСкачать

Сформулируйте используя законы де моргана отрицания следующих утверждений четырехугольник

Вопрос по математике:

Сформулируйте, используя законы де Моргана, отрицания следующих утверждений :
а) Четырехугольник АВСД – прямоугольник или параллелограмм;
б) Число 12 – четное и делится на 3.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Видео:Законы де Моргана || Формулы де Моргана || Правило де МорганаСкачать

Разработка урока «Построение отрицаний высказываний»

Разработка урока по теме «Построение отрицаний высказываний» по дисциплине ЕН.01. Математика для студентов , обучающихся по специальности 44.02.03. Педагогика дополнительного образования.

Просмотр содержимого документа
«Разработка урока «Построение отрицаний высказываний»»

ОБПОУ «Советский социально-аграрный техникум имени В.М.Клыкова».

Тема: Построение отрицаний высказываний.

Учебная дисциплина: ЕН.01. Математика

Специальность: 44.02.03. Педагогика дополнительного образования

Выполнила: преподаватель ОБПОУ «Советский социально-аграрный техникум имени В.М. Клыкова» Горбовская Т.Л.

Тема урока: Построение отрицаний высказываний.

Цель урока: Способствовать: формированию умения строить отрицания высказываний; обучению навыкам самостоятельного решения задач; развитию умения применять теоретические факты при решении задач;

Содействовать формированию навыков групповой работы, умения представлять свое решение, совместно устранять недочеты в решении; совершенствованию навыков монологической речи, приобретению умения видеть и исправлять недочеты своего доклада.

Создавать условия для развития критичности мышления.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 4. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и выполнения профессиональных задач, профессионального и личностного развития.

Тип урока: практический.

Форма проведения: математический бой

Учебная группа: 23

Оборудование: листы с распечатанными задачами, памятки для участников.

Организация начала урока.

Инструктаж по проведению математического боя.

Подведение итогов. Домашнее задание.

Организация начала урока. Сообщение целей и задач урока.

Инструктаж по проведению математического боя.

Учебная группа делится на две команды. Выбирается капитан каждой команды. Заранее готовятся преподавателем члены жюри (из числа обучающихся). Команды получают условия задач и время на их решение. Команды могут использовать записи в тетрадях, но не имеют права общаться по поводу решения задач ни с кем, кроме жюри. По истечении времени решения задач начинается бой, когда команды в соответствии с правилами рассказывают друг другу решение задач.

Если одна команда рассказывает решение, то другая оппонирует его, то есть ищет в нем ошибки или недостатки, и, если решения нет, то приводит свое. При этом выступление оппонента и докладчика оцениваются жюри в баллах (за решение и оппонирование). Если команды, обсудив предложенное решение, все – таки до конца задачу не решили или не обнаружили допущенные ошибки, то часть баллов (или все баллы) забирает себе жюри. Побеждает команда, которая по окончании боя набирает больше баллов.

Бой состоит из нескольких раундов. В начале каждого раунда одна из команд вызывает другую на одну из задач, решение которой еще не рассматривалось. После этого вызванная команда сообщает, принимает ли она вызов. Если вызов принят, то команда выставляет докладчика (который рассказывает и при необходимости записывает на доске) решение задачи, а вызвавшая команда выставляет оппонента, обязанность которого – искать ошибки. Если команда вызов не принимает, то докладчика обязана выставить та команда, которая сделала вызов, а команда отказавшаяся отвечать, выставляет оппонента. Если же команда, которая сделала вызов тоже отказывается рассказывать решение задачи, то ее вызов считается некорректным. Некорректным считается вызов и в том случае, если вызвавшая команда рассказала решение, но с ним не согласился оппонент, и это несогласие подтвердило жюри.

В начале раунда докладчик рассказывает решение. Доклад должен содержать ответ на все поставленные вопросы и доказательство правильности и полноты полученных ответов. Время доклада ограничивается 4 минутами.

Пока доклад не окончен, оппонент может задать вопросы докладчику только с согласия докладчика, но имеет право просить повторения части решения или разрешить докладчику не доказывать какие – то очевидные с точки зрения оппонента факты. После окончания доклада оппонент имеет право задавать вопросы докладчику.

Оппонент имеет право:

признать решение правильным;

решение (ответ) в основном правильным, но имеющим недостатки и (или) пробелы с обязательным их указанием;

признать решение (ответ) неправильным с указанием ошибок.

Если оппонент согласился с решением, то он и его команда в этом раунде больше не участвуют.

Оппонент обязан формулировать свои вопросы в вежливой, корректной форме; критикуя доклад, не допускать критики обидчика; повторять и уточнять свои вопросы по просьбе докладчика и жюри.

По окончании диалога докладчика и оппонента жюри задает свои вопросы. При необходимости оно может вмешиваться раньше.

Если оппонент доказал, что у докладчика нет решения, то оппонент получает право представить свое решение. При этом бывший докладчик становится оппонентом и может зарабатывать баллы за оппонирование.

Смена раундов влечет за собой смену вызывающей команды.

Каждый член команды имеет право выйти к доске в качестве докладчика или оппонента не больше двух раз за весь бой. Команда имеет право не более двух раз за бой заменять докладчика или оппонента, но при этом выход засчитывается как тому, кого заменили, так и тому, кто вышел на замену.

В любой момент боя команда, которая должна вызывать, может отказаться сделать это (если нет решения задач). Тогда другая команда получает право (но не обязана) рассказывать решение оставшихся задач. При этом вторая команда выставляет оппонентов и может получать баллы за оппонирование, но рассказывать решение она не имеет права.

Право первого вызова устанавливается конкурсом капитанов, который проводится в начале боя.

Каждая задача оценивается в 12 баллов, которые по итогам раунда распределяются между докладчиком, оппонентом и жюри. Если докладчик представил правильное и полное решение, то все 12 баллов достаются ему. Если же оппонент доказал, что докладчик не дал решения задачи, то происходит «смена ролей».

Размер штрафа за некорректный вызов объявляется командам до боя (до 6 баллов). Жюри является верховным толкователем правил боя. Решения жюри являются обязательными для команд.

Во время боя только капитан может от имени команды обращаться к жюри и соперникам: сообщать о вызове или отказе и т.д. если капитан у доски, то он оставляет за себя заместителя, исполняющего в это время обязанности капитана. Имена капитана и заместителя сообщаются жюри до начала боя. Во время решения задач главная обязанность капитана – координировать действия членов команды так, чтобы имеющимися силами решить как можно больше задач. Капитан с учетом пожеланий членов команды распределяет между ними задачи для решения, следит, чтобы каждая задача кем – то решалась, организует проверку найденных решений. Капитан заранее выясняет, кто будет докладчиком или оппонентом на той или иной задаче.

Жюри ведет на доске протокол боя. Если одна из команд не согласна с принятым жюри решением по задаче, то она имеет право немедленно потребовать перерыв на несколько минут для разбора ситуации с участием Председателя жюри.

После начала следующего раунда счет предыдущего раунда не может быть изменен. Жюри также следит за порядком во время боя (может оштрафовать команду за шум, некорректное поведение, общение со своим представителем, находящимся у доски).

Командам предлагаются следующие задачи (распечатаны для каждого участника):

Сформулируйте, используя законы де Моргана, отрицания следующих утверждений:

а) Четырехугольник ABCD – прямоугольник или параллелограмм.

б) Число 12 четное и делится на 3.

в) Число 28 нечетное или не делится на 4.

Какие из нижеприведенных предложений являются отрицанием высказывания «Все натуральные числа кратны 5»; свой выбор обоснуйте:

а) Все натуральные числа не кратны 5.

б) Существуют натуральные числа, не кратные 5.

в) Существуют натуральные числа, кратные 5.

г) Неверно, что все натуральные числа кратны 5.

д) Не все натуральные числа кратны 5.

Постройте двумя способами отрицание высказывания:

а) Всякое свойство квадрата присуще прямоугольнику.

б) Некоторые простые числа являются четными.

Определите, являются данные предложения отрицаниями друг друга, или нет; объясните почему:

а) Число 12 четное, число 12 – нечетное.

б) Все простые числа нечетны. Все простые числа четны.

в) Все простые числа нечетны. Существуют четные простые числа.

г) Некоторые углы острые. Некоторые углы тупые.

Переформулируйте данные предложения так, чтобы они не содержали слов «неверно, что», но имели тот же смысл:

а) Неверно, что число 9 – четное или простое.

б) Неверно, что треугольник ABC – равнобедренный и прямоугольный.

в) Неверно, что каждый четырехугольник является прямоугольником.

г) Неверно, что хотя бы в одном прямоугольнике диагонали взаимно перпендикулярны.

Постройте отрицания следующих высказываний и выясните, что истинно – данное высказывание или его отрицание:

а) Среди чисел есть такие, которые делятся на 5 и на 7.

б) Существуют числовые выражения, значения которых нельзя найти.

в) Частное чисел 25842 и 6 меньше разности чисел 14150 и 9833.

Сформулируйте отрицания следующих предложений двумя способами:

а) Число 123 делится на 9.

б) При делении числа 32 на 5 в остатке получится 7.

г) Треугольник ABC – прямоугольный.

Сформулируйте предложения, которые начинаются словами «неверно, что» и имеют тот же смысл, что и данные:

а) Прямые AB и CD не параллельны и не пересекаются;

б) Стороны четырехугольника ABCD не параллельны или не равны;

в) Существуют уравнения, не имеющие действительных корней;

г) Все прямоугольники не имеют равных смежных сторон.

Проводится конкурс капитанов, который не приносит очков, но даёт право вызова команде.

Вопрос для капитанов:

Как проверить, правильно ли построено отрицание высказывания?

В ходе математического боя оценивается не только работа команды, но и работа каждого участника команды (преподаватель ведет протокол).

Оценка каждого участника команды складывается из результатов защиты решения задачи (роль докладчика), работы в качестве оппонента, оценки команды.

Выступление жюри. Подведение итогов урока преподавателем. Отметки за урок.

Постройте двумя способами отрицание высказывания:

Произведение чисел 4070 и 8 меньше, чем сумма чисел 18396 и 14174;

Среди различных прямоугольников есть такие, площади которых равны.

Постройте отрицания следующих высказываний и выясните, что истинно – данное высказывание или его отрицание:

Сумма двух любых четных чисел есть число четное;

Хотя бы одно натуральное число является решением уравнения 7:х=2;

При делении числа 58 на 7 в остатке получится 3 или 7.

Видео:Законы алгебры логики / Закон де Моргана + доказательство [Алгебра логики] #5Скачать

Элемент ИЛИ. Логическое сложение

Элемент ИЛИ реализует функцию логического сложения или дизъюнкции.

Логическое сложение двух операндов x₁ и x₂, записывается следующим образом: ,

Условное графическое обозначение элемента И (рис. 6):

Рис.6 Условное графическое обозначение элемента ИЛИ

Математическое описание в форме таблице истинности элемента ИЛИ:

Таблица 3 — ТИ элемента ИЛИ

Словесно описание работы элемента ИЛИ выглядит следующим образом: на выходе будет присутствовать логическая единица тогда, и только тогда, когда хотя бы на одном входе есть логическая единица. Проиллюстрируем работу элемента ИЛИ следующими рисунками

Рис. 7 а, б, в, г. Иллюстрация работы элемента ИЛИ. Низкий уровень напряжения будет только в том случаи, когда на обоих входах присутствует низкий уровень напряжения а).

Описанные выше три логические элемента НЕ, И, ИЛИ являются основными и функционально достаточными элементами булевой алгебры.

Видео:2.4 Разность множеств, законы де Моргана | Константин Правдин | ИТМОСкачать

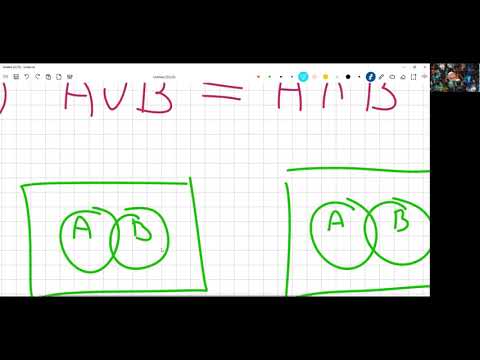
Законы де Моргана. Закон двойного отрицания

В системе булевой алгебры (далее булева алгебра) применяются три операции — конъюнкция, дизъюнкция, и отрицание. Эти операции выполняют цифровые элементы описанные выше И, ИЛИ, НЕ соответственно. Также выделяются две константы — 0 и 1. Для того чтобы производить преобразования над логическими выражениями, булева алгебра предоставляет ряд законов, аксиом и свойств.

Здесь не будут приводиться все аксиомы, свойства и законы булевой алгебры. Ограничимся рассмотрением трех законов — законов де Моргана и закона двойного отрицания. Свойства булевой алгебры, которые необходимо будет применить в следующих параграфах, будут оговариваться отдельно.

Законы де Моргана включают в себя два закона, которые связывают логические операции при помощи инверсии. Запишем их для двух операндов:

Т.е. при “разрыве” отрицания над логическим выражением меняется операция конъюнкция на дизъюнкцию (в первом законе) или дизъюнкции на конъюнкцию (во втором законе). Заметим, что отрицание, стоящее в правой части над всем выражением, исчезает в левой части, но остается в над каждым операндом по отдельности. Следует сделать ещё один вывод: операцию И можно реализовать с помощью элементов ИЛИ, и наоборот, операцию ИЛИ можно реализовать с помощью элементов И (что даёт создать полный базис, и значит реализовать любую логическую функцию, из операций И-НЕ или ИЛИ-НЕ, не используя систему из всех трёх основных операций И-ИЛИ-НЕ). Далее, говоря о применении закона де Моргана имеется в виду применение того закона из двух, которое ближе по смыслу.

Для примера преобразуем с помощью законов де Моргана следующие выражения:

Закон двойного отрицания или закон снятия двойного отрицания гласит: если неверно, что неверно утверждение x, то утверждение x верно. Или .

Отметим, что если два раза проинвертировать некое выражение, например , то его верность не изменится .

1. Преобразуем конъюнкцию операндов в дизъюнкцию:

Проинвертирует выражение два раза (смысл выражение не изменится):

Применим закон де Моргана:

2. Преобразуем конъюнкцию операндов в дизъюнкцию:

3. Преобразуем дизъюнкцию операндов в конъюнкцию:

Таким образом, применяя описанные выше законы, можно проводить преобразования в логических выражениях.

🔍 Видео

Конъюнкция, дизъюнкция, импликация, эквиваленция, отрицание. На примерах из жизни. Логика.Скачать

Логика и множества. Утверждения и отрицанияСкачать

Законы де Моргана. ЛогикаСкачать

Закон поглощения + доказательство. Преобразование логических выражений [Алгебра логики] #7Скачать

Секретный Квест "Изобильное Море" | Куча Скрытых Сундуков | Царство Фарахкерт Геншин 3.6Скачать

Удивительные примеры логикиСкачать

Операции над множествамиСкачать

Правила Де Моргана. Доказательство. Теория множеств.Скачать

Как устроено отрицание кванторов? Душкин объяснитСкачать

Лекция 67. Теорема де МорганаСкачать

Закон отрицания отрицания, 1982Скачать

Предикаты и кванторы. Отрицание предложений с кванторами.Скачать

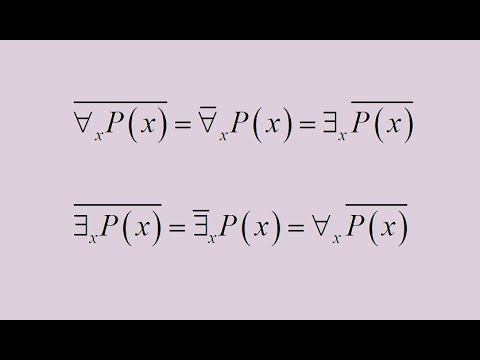
ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

Введение в логику, урок 4: Предикаты и кванторыСкачать

Отрицание, Дизъюнкция и Конъюнкция. Графическое решение логических выражений. Алгебра логики основыСкачать

Отрицание высказываний и высказывательных форм. (пункт 21. по учебнику Стойловой Л.П. Математика)Скачать