Delaunay.h — заголовочный файл
Delaunay.cpp — реализация.
- 1. Определения
- 1.1.Жадный алгоритм триангуляции
- 1.2. Триангуляция Делоне
- 2. Методы построения триангуляции Делоне
- 2.1. Итеративные алгоритмы
- 2.2. Алгоритмы триангуляции Делоне слиянием
- 2.3. Алгоритмы прямого построения
- 2.4. Двухпроходные алгоритмы
- 3. Имеющаяся реализация триангуляции Делоне
- 3.1. Описание алгоритма
- 3.2. Тонкое место
- 3.3. Время работы алгоритма
- 4. Литература
- 5. Реализация
- 6. Пример работы
- Триангуляция многоугольника
- Триангуляция многоугольников
- 📹 Видео
Видео:Построение натуральной величины треугольника методом вращенияСкачать

1. Определения
Определение. Триангуляцией называется планарный граф, все внутренние области которого являются треугольниками.
Определение. Триангуляция называется оптимальной, если сумма длин всех рёбер минимальна среди всех возможных триангуляций, построенных на тех же исходных точках.
Для большинства реальных задач существующие алгоритмы построения оптимальной триангуляции неприемлемы ввиду слишком высокой трудоёмкости. При необходимости на практике применяют приближенные алгоритмы, например «жадный» алгоритм построения триангуляции или триангуляцию Делоне.
1.1.Жадный алгоритм триангуляции
Шаг 1. Генерируется список всех возможных отрезков, соединяющих пары исходных точек, и он сортируется по длинам отрезков.
Шаг 2. Начиная с самого короткого, последовательно выполняется вставка отрезков в триангуляцию. Если отрезок не пересекается с другими ранее вставленными отрезками, то он вставляется, иначе он отбрасывается.
Заметим, что если все возможные отрезки имеют разную длину, то результат работы этого алгоритма однозначен, иначе он зависит от порядка вставки отрезков одинаковой длины.
Трудоемкость работы жадного алгоритма при некоторых его улучшениях составляет
O(N 2 logN) [3]. В связи со столь большой трудоемкостью на практике он почти не применяется.
1.2. Триангуляция Делоне
Пусть на плоскости дан набор точек <Pi=(xi,yi)>. Триангуляцией Делоне называется такое разбиение плоскости на треугольники с вершинами в заданных точках, что ни одна окружность, описанная вокруг любого из треугольников, не содержит других точек из разбиения.
Другое определение триангуляции Делоне дают два следующих определения.
Определение. Говорят, что пара соседних треугольников триангуляции удовлетворяет условию Делоне, если этому условию удовлетворяет триангуляция, составленная только из этих двух треугольников.
Определение. Говорят, что треугольник триангуляции удовлетворяет условию Делоне, если этому условию удовлетворяет триангуляция, составленная только из этого треугольника и трёх его соседей (если они существуют).
Триангуляция Делоне всегда существует. Чаще всего она единственная, но в некоторых случаях (см.ниже) таких триангуляций существует несколько.
Многие алгоритмы построения триангуляции Делоне используют следующую теорему:
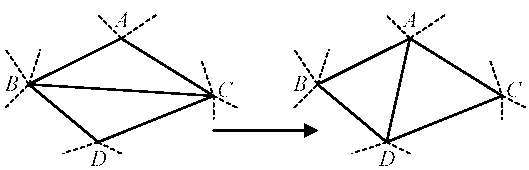
Теорема 1. Триангуляцию Делоне можно получить из любой другой триангуляции по той же системе точек, последовательно перестраивая пары соседних треугольников (ABC) и (BCD), не удовлетворяющих условию Делоне, в пары треугольников (ABD) и (ACD) (см.рис.). Такая операция перестроения также часто называется флипом (flip).
Теорема 2. Триангуляция Делоне обладает максимальной суммой минимальных углов всех своих треугольников среди всех возможных триангуляций.
Теорема 3. Триангуляция Делоне обладает минимальной суммой радиусов окружностей, описанных около треугольников, среди всех возможных триангуляций.
Видео:Математика без Ху!ни. Вычисление определителя методом треугольников.Скачать

2. Методы построения триангуляции Делоне
В настоящее время известно значительное количество различных алгоритмов построения триангуляции Делоне. Их можно разделить на следующие группы:
- Итеративные алгоритмы
- Алгоритмы слияния
- Алгоритмы прямого построения
- Двухпроходные алгоритмы.
2.1. Итеративные алгоритмы
Все итеративные алгоритмы имеют в своей основе очень простую идею последовательного добавления точек в частично построенную триангуляцию Делоне. Формально это выглядит так.
Итеративный алгоритм построения триангуляции Делоне.
Дано множество из N точек.
- Шаг 1. На первых трех исходных точках строим один треугольник.
- Шаг 2. В цикле по n для всех остальных точек выполняем шаги 3–5.
- Шаг 3. Очередная n-я точка добавляется в уже построенную структуру триангуляции следующим образом. Вначале производится локализация точки, т.е. находится треугольник (построенный ранее), в который попадает очередная точка. Либо, если точка не попадает внутрь триангуляции, находится треугольник на границе триангуляции, ближайший к очередной точке.
- Шаг 4. Если точка попала на ранее вставленный узел триангуляции, то такая точка обычно отбрасывается, иначе точка вставляется в триангуляцию в виде нового узла. При этом если точка попала на некоторое ребро, то оно разбивается на два новых, а оба смежных с ребром треугольника также делятся на два меньших. Если точка попала строго внутрь какого-нибудь треугольника, он разбивается на три новых. Если точка попала вне триангуляции, то строится один или более треугольников.
- Шаг 5. Проводятся локальные проверки вновь полученных треугольников на соответствие условию Делоне и выполняются необходимые перестроения.
- Конец алгоритма.
Различные версии этого алгоритма различаются способом выбора очередной точки и методом локализации, последовательностью перестроений.
2.2. Алгоритмы триангуляции Делоне слиянием
В целом, все алгоритмы слияния предполагают разбиение исходного множества точек на несколько подмножеств, построение триангуляций на этих подмножествах, а затем объединение (слияние) нескольких триангуляций в одно целое.
Например, множество точек разбивается на две как можно более равные части с помощью горизонтальных и вертикальных линий. Алгоритм триангуляции рекурсивно применяется к подчастям, а затем производится слияние (объединение, склеивание) полученных подтриангуляций.
В других вариантах триангуляции разбиение на части производится путем выбора диаметра – самого длинного отрезка между данными точками, путем разбиения точек на горизонтальные и/или вертикальные полосы и т.д.
2.3. Алгоритмы прямого построения
(Алгоритм такого типа а у нас и используется в настоящее время)
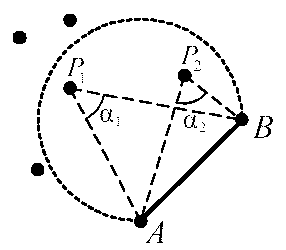
Во всех вариантах этого алгоритма мы начинаем с некоторого начального (базового) отрезка, расположенного на границе. Далее для него необходимо найти соседа Делоне – узел, который вместе с концами данного базового отрезка в триангуляции Делоне является вершинами одного треугольника. Процесс поиска можно представить как рост «пузыря» от базового отрезка, пока не встретится какой-нибудь узел. «Пузырь» – это окружность, проходящая через точки A и B, и центр которой находится на срединном перпендикуляре к базовому отрезку.
В пошаговом алгоритме для поиска соседа Делоне нужно выбрать среди всех точек Pi триангуляции такую, что угол APiB будет максимальным. Найденный сосед Делоне соединяется отрезками с концами базовой линии и образует треугольник APiB. Новые рёбра APi и BPi построенного треугольника помечаются как новые базовые отрезки, и процесс поиска треугольников продолжается.
Трудоемкость пошагового алгоритма составляет
O(N 2 ) в среднем и в худшем случае.
Цитата из книги [1]: «Из-за столь большой трудоемкости на практике такой алгоритм почти не применяется». Но мы как раз его и используем. В основном из-за того, что этот алгоритм несколько проще в реализации. Кроме того, при количестве точек
100-500 алгоритм все-таки работает достаточно быстро.
2.4. Двухпроходные алгоритмы
При построении триангуляции Делоне итеративными алгоритмами и алгоритмами слияния для каждого нового треугольника должно быть проверено условие Делоне. Если оно не выполняется, то должны последовать перестроения треугольников и новая серия проверок. На практике довольно большую долю времени отнимают как раз проверки на условие Делоне и перестроения. Для уменьшения числа проверок условия Делоне и упрощения логики работы алгоритмов можно использовать следующий подход. Вначале за первый проход нужно построить некоторую триангуляцию, игнорируя выполнение условия Делоне. А после этого за второй проход проверить то, что получилось, и провести нужные улучшающие перестроения для приведения триангуляции к условию Делоне.
Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

3. Имеющаяся реализация триангуляции Делоне
3.1. Описание алгоритма
Имеющаяся на сегодняшний день реализация алгоритма триангуляции Делоне, с точки зрения описанной выше классификации, является одной из разновидностей алгоритма «прямого построения триангуляции».
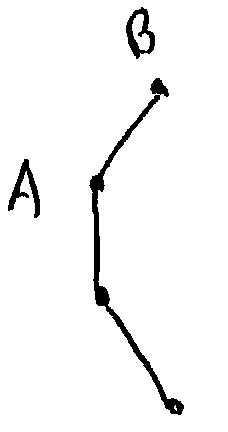
Опишем сначала общую схему алгоритма. В начале найдем первое ребро, которое заведомо должно войти в триангуляцию. Первая его точка (A на рисунке справа) выбирается как точка с наименьшей координатой x (самая левая точка), а среди точек с одинаковой координатой x – как точка с наименьшей координатой y (самая верхняя). Вторая точка начального ребра (B на рисунке) – это точка с наибольшим коэффициентом наклона отрезка [AB].
Список edges – сплошные ребра,
edges_all – сплошные и пунктирные
В процессе работы алгоритма поддерживаются список активных ребер edges. «Активные» ребра – это те, у которых с одной стороны уже есть треугольник, а с другой еще надо пристраивать.
В начале работы он состоит из единственного ребра [AB]. В это список одни ребра добавляются, другие удаляются. Алгоритм заканчивает работу, когда этот список становится пустым.
Дальнейший алгоритм состоит в повторении следующих шагов: выбор очередного ребра из списка edges (и удаление его из списка), и нахождении для него присоединенной вершины – узла, который вместе с концами выбранного ребра в триангуляции Делоне образует вершины одного треугольника. Процесс поиска можно представить как рост «пузыря» от выбранного ребра [AB], пока не встретится какой-нибудь узел. «Пузырь» – это окружность, проходящая через точки A и B, и центр которой находится на срединном перпендикуляре к отрезку.
Фактически, мы выбираем среди всех заданных точек Pi такую, что угол APiB будет максимальным, или, что то же самое – радиус окружности, проходящей через точки APiB будет наименьшим. Найденная присоединенная вершина соединяется отрезками с концами отрезка и образует треугольник APiB. Новые рёбра APi и BPi построенного треугольника добавляются в список edges (если их там еще нет), и процесс поиска треугольников продолжается.
При добавлении ребер в список активных, мы вначале проверяем, нет ли там уже этого ребра. Если нет – то просто добавляем. Если уже есть, это означает, что обработка ребра завершена и его надо удалить из списка.
3.2. Тонкое место
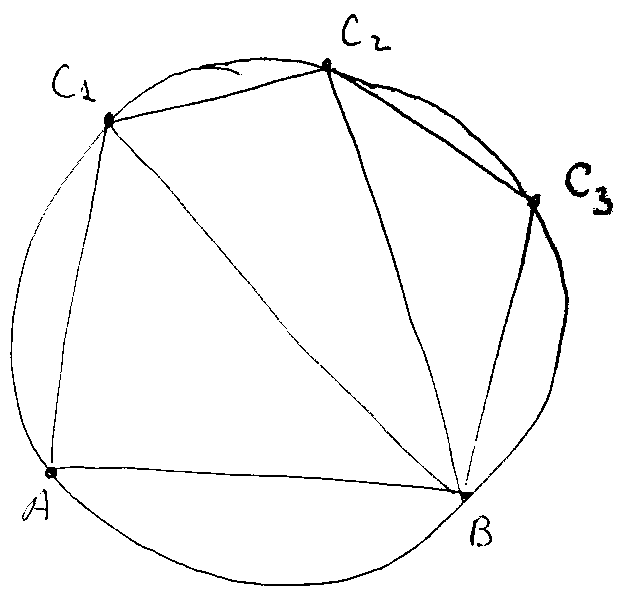
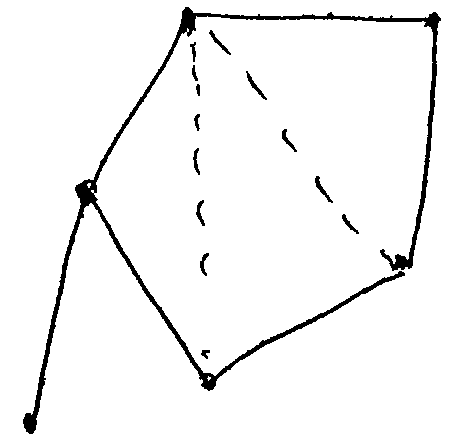
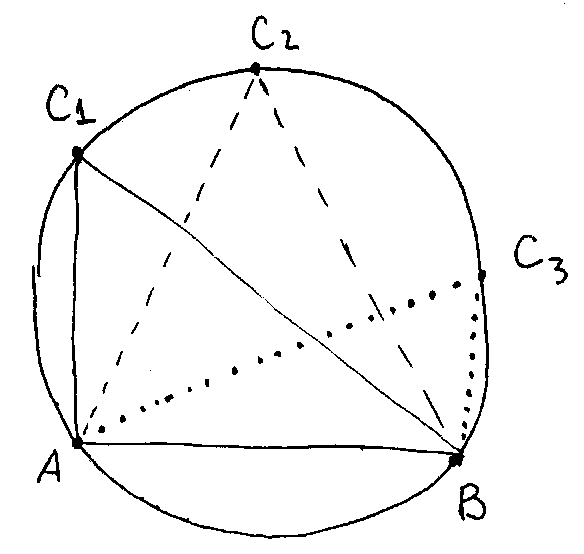
Если точек P с наименьшим радиусом окружности оказывается несколько (рис. слева), надо не выбирать какую-то одну из этих точек, а сразу добавить все получающиеся треугольники и, соответственно, модифицировать список активных ребер. На рисунке справа добавляемые треугольники – это AC1B, C1C2B, C2C3B и активные ребра AC1, C1C2, C2C3, C2C3B.
3.3. Время работы алгоритма
Этот алгоритм для вычисления триангуляции Делоне по набору из n точек выполняется за время О(n 2 ), поскольку при каждой итерации в полный список ребер добавляется ровно одно ребро. Поэтому число итераций равно числу ребер в триангуляции Делоне. Согласно теореме о триангуляции набор точек любая триангуляция содержит не более, чем О(n) ребер, поэтому алгоритм выполняет О(n) итераций. Поскольку на каждую итерацию тратится время О(n), то полностью алгоритм выполняется за время О(n 2 ).
Приведем результаты более точных экспериментов на процессоре Pentium 2.4 Ghz. Так как алгоритм не требует большого объема памяти и не обращается к внешним устройствам, то остальные характеристики компьютера не должны оказывать влияния на скорость работы.
| Количество узлов | Время триангуляции (миллисекунд) |
|---|---|
| 10 | 0.025 |
| 100 | 1.9 |
| 1000 | 172 |
| 10000 | 17500 |
Видео:Лекция 1. Точка на прямой. Метод прямоугольного треугольникаСкачать

4. Литература
- Скворцов А.В. Триангуляция Делоне и её применение. Томск. 2002. 128 с.
- Ruppert J., A Delaunay Refinenent Algorith for Quality 2-Dimensional Mesh Generation. NASA Research Center Journal, 1994-feb.
- Gilbert P.N. New results on planar triangulations. Tech. Rep. ACT-15, Coord. Sci. Lab., University of Illinois at Urbana, July 1979.
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

5. Реализация
Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

6. Пример работы
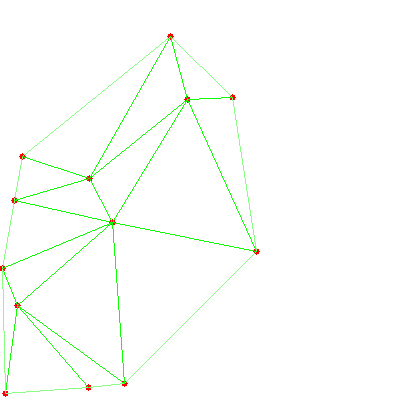
Пример работы: 

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Триангуляция многоугольника
Системы синтеза реалистических изображений должны обеспечивать передачу всех свойств моделируемого объекта: объемность, расположение, передачу полутонов, тени, освещение, текстуры поверхности. Чем выше степень реалистичности изображения, тем больше требуется вычислений для его формирования.
Генерация объемных изображений представляет сложную вычислительную задачу, в связи этим на практике выполняют ее декомпозицию. Сложные изображения формируют из фрагментов объектов, для чего их разбивают на составные части. Процесс разбиения поверхности объектов на полигоны получил название тесселяции.
В настоящее время появилось большое разнообразие графических акселераторов, которые имеют различные аппаратные графические функции для закраски трехмерных объектов, удаления невидимых частей, наложения текстур и т.п. Для использования преимуществ 3D-ускорителей необходимо сначала программно произвести тесселяцию исходных объектов, а затем передать полученные полигональные области для дальнейшей обработки акселератору.
На практике наиболее часто производится разбиение изображений на треугольники.
Это объясняется следующими причинами:
• треугольник является простейшим полигоном, вершины которого однозначно задают грань;
• любую область можно гарантировано разбить на треугольники;
• вычислительная сложность алгоритмов разбиения на треугольники существенно меньше, чем при использовании других полигонов;
• реализация процедур рендеринга наиболее проста для области, ограниченной треугольником;
• для треугольника легко определить три его ближайших соседа, имеющих с ним общие грани.
Процесс разбиения полигональной области со сложной конфигурацией в набор треугольников называется триангуляцией. При анализе или синтезе сложных поверхностей их аппроксимируют сеткой треугольников, и впоследствии оперируют с простейшими полигональными областями, т.е. с каждым из треугольников.
Алгоритм триангуляции:
1. Берем три вершины A1, A2, A3
2. Проверяем образуют ли вектора A1A3, A1A2 и их векторное произведение левую тройку векторов.
3. Проверяем нет ли внутри треугольника A1A2A3 какой-либо из оставшихся вершин многоугольника.
4. Если оба условия выполняются, то строим треугольник A1A2A3, а вершину A2 исключаем из многоугольника, не трогая вершину A1, сдвигаем вершины A2 (A2 на A3), A3 (A3 на A4)
5. Если хоть одно условие не выполняется, переходим к следующим трем вершинам.
6. Повторяем с 1 шага, пока не останется три вершины.
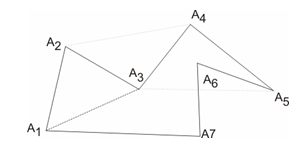
Рис.1 Алгоритм триангуляции невыпуклого многоугольника
На рисунке 1
• треугольник A1A2A3 удовлетворяет обоим условиям (п.2, п.3);
• треугольник A2A3A4 не удовлетворяет условию (п.2);
• треугольник A3A4A5 не удовлетворяет условию (п.3).
Видео:Вычислить определитель 3 порядка. Правило треугольникаСкачать

Триангуляция многоугольников
Задача: разбить произвольный многоугольник на треугольники.
- Клас, что-то наподобие списка, где можно двигаться вперед-назад и конец соединен с началом. То есть замкнутый круг, элементами которого будут объекты описаны пунктом ниже.
- Клас для представления точки. В нем, как полагается, должны быть координаты х и у. Так же еще одно поле в котором записано значение угла соответствующего этой точке в многоугольнике
- Функция, на вход которой идут два векторы, а на выход — угол между ними
- Функция, на вход которой идет точка и треугольник, на выход — признак, лежит ли точка внутри треугольника.
Теперь сам алгоритм.
Подготовка рабочих объективов.
Результатом работы должен быть список треугольников (result), потому создаем пустой список. Рабочий двунаправленный замкнутый список (points), представляющий многоугольник.
Перед стартом просчитываем углы для всех точек многоугольника.
Выбираем любую точку многоугольника как «рабочую» (p(i)).
- Создаем пустой список для хранения временных треугольников.
Если точка слева от «рабочий» (p(i)->left) имеет угол меньше чем 180 градусов и треугольник (p(i), p(i)->left, p(i)->left->left) не содержит внутри себя других точек многоугольника — заносим этот треугольник в наш временный список.
Если точка справа от «рабочий» (p(i)->right) имеет угол меньше чем 180 градусов и треугольник (p(i), p(i)->right, p(i)->right->right) не содержит внутри себя других точек многоугольника — заносим этот треугольник в наш временный список.
Если «рабочая» точка (p(i)) имеет угол меньше чем 180 градусов и треугольник ( p(i)->left, p(i),p(i)->right) не содержит внутри себя других точек многоугольника — заносим этот треугольник в наш временный список. - Если временный список не содержит треугольников — выбираем вместо «рабочий», точку слева от нее и возвращаемся к первому пункту.
Если содержит — выбираем треугольник с минимальной разницей между минимальным и максимальным углом (нужно пересчитать значение углов), заносим его в список result, удаляем из points среднюю точку из треугольника который выбрали а соседним точкам от нее (в points) пересчитываем значения углов, первую точку выбираем в качестве «рабочей» (p(i)).Если в points осталось только две точки — прекращаем работу, список треугольников содержится в res, иначе возвращаемся к первому пункту.
Теперь пара слов об оптимизации алгоритма.
На втором этапе выбирается треугольник с минимальной разницей между минимальным и максимальным углом для того, чтобы треугольник был максимально подобный к правильному, иногда это важно. Если же вам нет разницы как выглядит треугольник — тогда можно не создавать временный список треугольников, а выбрать первый из трех возможных треугольников который не содержит внутри себя другую точку многоугольника и угол, который образует средняя точка треугольника в многоугольнике меньше 180 градусов. Такое упрощение значительно снизит вычислительные затраты.
Еще, если уверены, что многоугольник выпуклый — тогда не нужно проверь содержит ли треугольник другие точки многоугольника.
П.С. Я не встречал такой алгоритм на просторах инета, хотя и уверен, что что-то подобное уже есть.
📹 Видео
Метод прямоугольников для нахождения определенного интегралаСкачать

🔥 ФОКУС с треугольником #shortsСкачать

Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Как строить сеченияСкачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Определение натуральной величины треугольника АВС методом совмещенияСкачать

Треугольники. 7 класс.Скачать

Нахождение натуральной величины треугольника. Метод замены плоскостей проекцийСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Приведение определителя к треугольному видуСкачать

Подобные треугольники с нуля до ОГЭ | Математика ОГЭ 2023 | УмскулСкачать