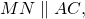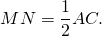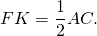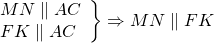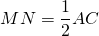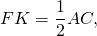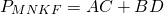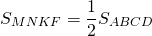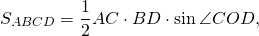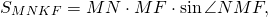Середины сторон выпуклого четырехугольника являются вершинами

В школьном курсе теорема Вариньона часто фигурирует в качестве обычной задачи, в которой требуется доказать, что середины сторон четырёхугольника являются вершинами параллелограмма.

Её доказательство основано на свойствах средней линии треугольника.

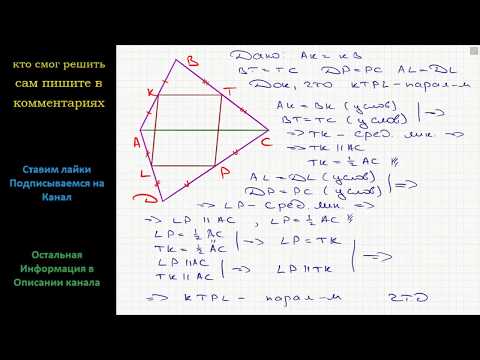
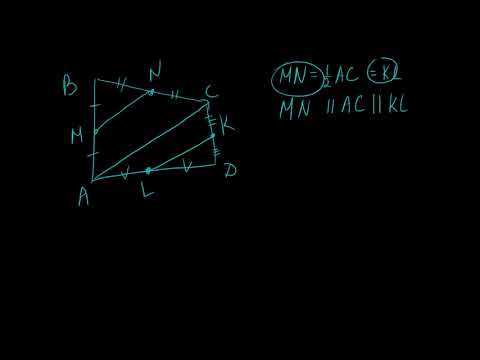
Середины сторон четырёхугольника являются вершинами параллелограмма.

Дано: ABCD — четырёхугольник,

M, N, K, F — середины его сторон.

Доказать : MNKF — параллелограмм.

1) Проведём диагональ AC.

2) Рассмотрим треугольник ABC.

Так как точки M и N — середины сторон AB и BC, отрезок MN — средняя линия треугольника ABC.

3) Аналогично, FK — средняя линия треугольника ADC и

4) По признаку параллельности прямых, две прямые, параллельные третьей прямой, параллельны между собой:

5) В четырёхугольнике MKNF противоположные стороны параллельны и равны. Следовательно, MKNF — параллелограмм (по признаку).

Что и требовалось доказать.

Поскольку в школьном курсе геометрии рассматриваются только выпуклые четырёхугольники, доказательство приведено только для этого случая. Но и для невыпуклых четырёхугольников (в том числе, и для самопересекающихся), теорема также верна (доказывается аналогично).

Параллелограмм, образованный серединами сторон четырёхугольника, называется параллелограммом Вариньона (вариньоновским, вариньоновым).

Периметр параллелограмма Вариньона равен сумме диагоналей исходного параллелограмма:

(так как стороны MNKF равны половине диагонали AC или BD).

Площадь параллелограмма Вариньона равна половине площади исходного параллелограмма:

углы COD и NMF равны (как внутренние накрест лежащие при параллельных прямых AC и MN и секущей BD),

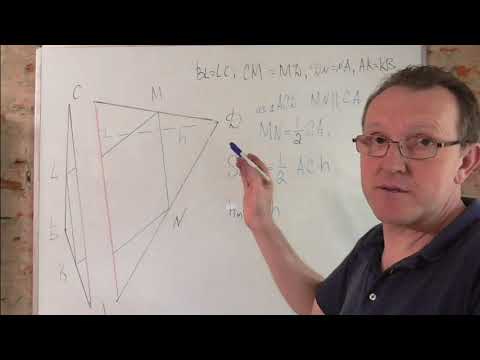
Видео:№43. Докажите, что середины сторон пространственного четырехугольника* являютсяСкачать

Докажите, что середины сторон выпуклого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади данного четырёхугольника.

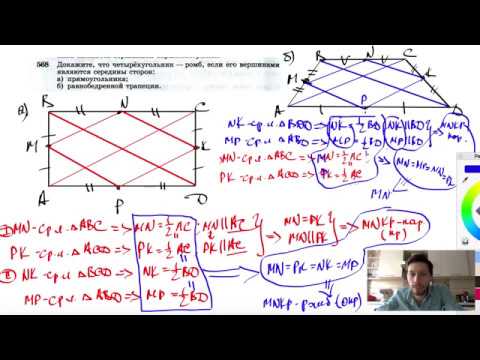
Видео:№568. Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон:Скачать

Ваш ответ

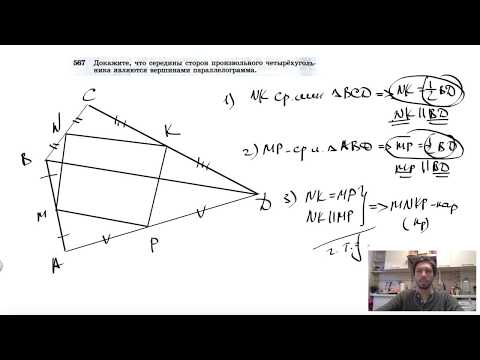
Видео:№567. Докажите, что середины сторон произвольного четырехугольника являютсяСкачать

решение вопроса

Видео:Геометрия Вершины четырехугольника являются середины сторон прямоугольника с диагональю 12 смСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,658
• разное 16,822

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

Урок геометрии по теме «Теорема Вариньона. Решение задач». 8-й класс

Класс: 8

Презентация к уроку

Загрузить презентацию (276 кБ)

Цель: изучить теорему Вариньона и научиться применять ее на практике с наименьшими временными затратами.

Задачи:

1. Изучить теоретический материал: понятия «параллелограмм Вариньона», бимедианы четырехугольника, разобрать доказательство теоремы Вариньона и следствия из нее.
2. Сравнить количество времени, необходимое для решения задач традиционным способом и, используя теорему Вариньона.
3. Показать решение олимпиадных заданий с помощью параллелограмма Вариньона.

Видео:№163. Докажите, что середины сторон равнобедренного треугольника являются вершинами другого равнобедСкачать

Ход урока

Введение

В 21 век, в век информационных технологий, главным ресурсом является время. Тысячи людей желают посещать тренинги, семинары и лекции по тайм-менеджменту, где бы их научили, как рационально, с минимальными потерями и максимальной пользой использовать свое время. Большую часть времени у ученика занимает обучение в школе и приготовление домашнего задания. Одним из самых сложных предметов в школе является геометрия. В частности, задачи на доказательство требуют значительной траты времени, поэтому у многих отсутствует интерес к решению подобных заданий. В теме «Четырехугольники» эту проблему может решить использование теоремы Вариньона.

Пьер Вариньон – французский математик и механик 18 века, который первым доказал, что середины сторон выпуклого четырехугольника являются вершинами параллелограмма. Эта теорема вызвала интерес у отечественных ученых лишь в 20 веке. Подробно ее применение показал украинский геометр – Г.Б.Филипповский и кандидат физико-математических наук, доцент МГУ В.В. Вавилов. В школе теорема Вариньона не входит в курс программы, но считаю изучение её необходимым.

1. Теоретическая часть

Вариньон Пьер [1] (1654–1722)

Пьер Вариньон родился во Франции в 1654 году. Обучался в иезуитском коллеже и университете в Кане, где стал магистром в 1682 году. Вариньон готовился к религиозной деятельности, но, изучая сочинения Эвклида и Декарта, увлекся математикой и механикой. Труды Вариньона посвящены теоретической механике, анализу бесконечно малых, геометрии, гидромеханике и физике. Вариньон был одним из первых ученых, ознакомивших Францию с анализом бесконечно малых. В конце 17 и начале 18 в. Вариньон руководил «Журналом ученых», в котором помещали свои работы по исчислению бесконечно малых братья Бернулли. В геометрии Вариньон изучал различные специальные кривые, в частности ввел термин «логарифмическая спираль». Главные заслуги Вариньона относятся к теоретической механике, а именно к геометрической статике. В 1687 Вариньон представил в Парижскую АН сочинение «Проект новой механики. », в котором сформулировал закон параллелограмма сил. В 1725 в Париже был издан трактат Вариньона «Новая механика или статика», представляющий собой систематическое изложение учения о сложении и разложении сил, о моментах сил и правилах оперирования ими, почти без изменений сохранившееся в учебниках статики до нашего времени. Написал учебник по элементарной геометрии (издан в 1731).

Теорема Вариньона [2]

Четырехугольник, образованный путем последовательного соединения середин сторон выпуклого четырехугольника, является параллелограммом, и его площадь равна половине площади данного четырехугольника.

ABCD – выпуклый четырехугольник

AK=KB; BL=LC; CM=MD; AN=ND

1) KLMN – параллелограмм;

1. Рассмотрим одну из сторон четырехугольника KLMN, например KL. KL– средняя линия треугольника ABC(по определению),следовательно, KL║AC. Аналогично, так как MN– средняя линия треугольника ADC,то MN║AC. Так как KL║AC и MN║AC следовательно, KL║NM и KL=MN=AC/2. Таким образом, KLMN – параллелограмм. Этот параллелограмм называется параллелограммом Вариньона данного четырехугольника.
2. Средняя линия треугольника отсекает от него треугольник, площадь которого в четыре раза меньше площади исходного треугольника,
3. т.е. S_KBL = S_ABC/4, S_MDN=S_ADS/4. Следовательно, S₁+S₃=S_ABCD /4. Аналогично, S₂+S₄=S_ABCD/4. Следовательно, S₁+S₃ + S₂+S₄ = S_ABCD /4 + S_ABCD/4 = S_ABCD/2.

Т.е., SKLMN = S_ABCD/2. Что и требовалось доказать.

Определение. Бимедианы четырехугольниках [3] – это отрезки, соединяющие середины противоположных сторон (диагонали параллелограмма Вариньона)

Следствия из теоремы Вариньона

Параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны 2) бимедианы перпендикулярны.

Доказать: KLMN – ромб

Так как AC=BD (диагонали исходного четырехугольника равны по условию), то стороны параллелограмма Вариньона будут равны KL=LM=MN=NK (используя свойство средних линий треугольников, образованных при пересечении диагоналей исходного четырехугольника). Параллелограмм c равными сторонами является ромбом.

KLMN – параллелограмм Вариньона;

KM и LN перпендикулярны

Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом (по признаку ромба).

Что и требовалось доказать.

Параллелограмм Вариньона является прямоугольником тогда и только тогда, когда в исходном четырехугольнике: 1) диагонали перпендикулярны; 2) бимедианы равны

KLMN – параллелограмм Вариньона;

диагонали AC и BD – перпендикулярны

Так как диагонали AC и BD – перпендикулярны, то стороны параллелограмма Вариньона будут перпендикулярны. Следовательно, параллелограмм Вариньона является прямоугольником.

KLMN – параллелограмм Вариньона;

бимедианы KM и LN – равны

Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником (по признаку прямоугольника).

Что и требовалось доказать.

Параллелограмм Вариньона является квадратом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны и перпендикулярны; 2) бимедианы равны и перпендикулярны

KLMN – параллелограмм Вариньона;

диагонали AC и BD – перпендикулярны; AC=BD

Так как диагонали исходного четырехугольника AC и BD равны и перпендикулярны, то стороны параллелограмма Вариньона будут равны и перпендикулярны. Следовательно, параллелограмм Вариньона является квадратом.

KLMN – параллелограмм Вариньона;

бимедианы KM и LN – перпендикулярны; KM=LN

Доказать: KLMN – квадрат

Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом (по признаку квадрата).

Что и требовалось доказать.

2. Практическая часть. Решение задач.

Докажите, что а) середины сторон прямоугольника являются вершинами ромба. И наоборот, б) середины сторон ромба являются вершинами прямоугольника.

а) Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба (см. следствие 1);

Стороны прямоугольника перпендикулярны, поэтому бимедианы перпендикулярны, тогда середины сторон прямоугольника являются вершинами ромба (см. следствие 1).

б) диагонали ромба перпендикулярны, поэтому середины сторон ромба являются вершинами прямоугольника (см. следствие 2);

Стороны ромба равны, поэтому середины сторон ромба являются вершинами прямоугольника (см. следствие 2).

У четырехугольника диагонали равны aи b. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

Периметр параллелограмма Вариньона равен a+b.

Докажите, что середины сторон четырехугольника являются вершинами параллелограмма.

См. теорему Вариньона.

Докажите, что средние линии четырехугольника делятся точкой пересечения пополам.

Т.к. средние линии четырехугольника являются диагоналями параллелограмма Вариньона, то точка пересечения делит их пополам.

Олимпиадные задачи

1. Докажите, что если диагонали четырехугольника равны, то его площадь равна произведению средних линий [5].

Доказать: S_ABCD= KM*LN

Так как диагонали AC = BD, параллелограмм Вариньона является ромбом, площадь ромба равна половине произведения его диагоналей.

Что и требовалось доказать.

2. Докажите, что суммы площадей накрест лежащих четырехугольников, образованных пересечением бимедиан LN и KM выпуклого четырехугольника ABCD равны [6].

Воспользуемся теоремой о средней линии треугольника.

Что и требовалось доказать.

Заключение

«Нет ничего нового под солнцем, но есть кое-что старое, чего мы не знаем», – сказал американский литератор Лоренс Питер.

Пьер Вариньон жил в 18 веке, но теорема Вариньона как нельзя актуальна именно в наши дни, когда чтобы всё успеть, необходимо гораздо больше, чем 24 часа в сутки.

Поэтому была поставлена цель: изучить теорему Вариньона и научиться применять ее на практике с наименьшими временными затратами.

Для этого был разобран весь теоретический материал, решены задачи базового уровня, а также повышенной сложности (олимпиадные). Было подсчитано, что на решение задачи традиционным способом затрачивается 15-20 минут, а зная теорему Вариньона и следствия из нее, доказательство сводится к одному-двум предложениям и занимает 1-2 минуты. При этом экономия времени на доказательство в среднем составляет 15 минут. Таким образом, уже даже решение трех задач добавит дополнительные сорок пять минут (т.е. целый урок) на доказательство других, более сложных.

От этого повышается не только интерес к изучению данного предмета, но и сам процесс работы приносит удовлетворение. Цель работы считаю достигнутой.

🎥 Видео

Геометрия Вершинами четырехугольника являются середины сторон ромба с диагоналями 8 см и 14 смСкачать

Геометрия Докажите, что середины сторон четырехугольника являются вершинами параллелограммаСкачать

Задача первоклассника в 1 шаг! Невероятное решение!Скачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Геометрия Диагонали выпуклого четырехугольника ABCD перпендикулярны. Через середины сторон AB и ADСкачать

Планиметрия_03_01Скачать

Четырехугольники. Геометрия 8 класс.Скачать

9 класс. Геометрия. ОГЭ. Окружность. Четырехугольники.Скачать

Теорема Вариньона. Середины сторон четырёхугольника.Скачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

8 класс, 3 урок, ЧетырехугольникСкачать

ЕГЭ Математика Задание 6#27845Скачать

Теорема Вариньона | Середины сторон четырехугольникаСкачать

Диагонали четырехугольника равны 4 и 5.Скачать