Четырехугольники его элементы презентация

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

ЧЕТЫРЕХУГОЛЬНИК И ЕГО ЭЛЕМЕНТЫ

Ц Е Л Ь — ознакомить учащихся с понятием четырехугольника; — ввести терминологию, связанную с элементами четырехугольника; — распознавать выпуклые многоугольники; — сумма углов выпуклого четырехугольника;

ЧЕТЫРЕХУГОЛЬНИКОМ Называется фигура, которая состоит из четырех точек (это вершины четырехугольника) и четырех отрезков, последовательно соединяющих эти точки (это стороны четырехугольника). При этом никакие три из этих точек не лежат на одной прямой, а отрезки, их соединяющие, не пересекаются. А В С D

невыпуклый P Q L R A B C D выпуклый ВЫПУКЛЫЙ И НЕВЫПУКЛЫЙ ЧЕТЫРЕХУГОЛЬНИК

M N F K СОСЕДНИЕ ВЕРШИНЫ

M N F K ПРОТИВОЛЕЖАЩИЕ ВЕРШИНЫ

M N F K Д И А Г О Н А Л И

M N F СОСЕДНИЕ СТОРОНЫ

M N F K ПРОТИВОЛЕЖАЩИЕ СТОРОНЫ

СУММА УГЛОВ ВЫПУКЛОГО ЧЕТЫРЕХУГОЛЬНИКА (n – 2)·180º 360º

АУКЦИОН «ЧЕТЫРЕХУГОЛЬНИК» В С А D

Вилкова Ирина Борисовна учитель математики МОУ лицей «МОК №2» г. Джанкой 2015 г.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 958 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 333 человека из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 683 человека из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Вилкова Ирина БорисовнаНаписать 4549 11.08.2015

Номер материала: ДA-003951

11.08.2015 4642

11.08.2015 666

11.08.2015 586

11.08.2015 411

11.08.2015 519

11.08.2015 355

11.08.2015 1526

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Россия направит $10,3 млн на развитие школьного питания в нескольких странах

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Во всех педвузах страны появятся технопарки

Время чтения: 1 минута

Названы главные риски для детей на зимних каникулах

Время чтения: 3 минуты

Все школы РФ с 2023 года подключат к государственной информационной системе «Моя школа»

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:ЧЕТЫРЕХУГОЛЬНИК и его элементы. §1 геометрия 8 классСкачать

Презентация по теме «Четырехугольник и его элементы»
презентация к уроку по геометрии (8 класс) по теме

Презентация к уроку геометрии 8 класса по теме «Четырехугольник и его элементы» (учебник «Геометрия, 8 класс», автор А.Г.Мерзляк)

Видео:Четырёхугольник и его элементы – 8 класс геометрияСкачать

Скачать:

Бесплатный марафон подготовки к ЕГЭ на зимних каникулах

Учи.Дома запускает бесплатный марафон в котором каждый день. В течении 5 дней утром ты будешь получать одно задание по выбранному предмету, а вечером его решение. Твоя задача, успеть выполнение задание до того как получишь ответ.

Бесплатно, онлайн, подготовка к ЕГЭ

Предварительный просмотр:

Видео:Геометрия 8 класс. Урок 1. Четырехугольник и его элементыСкачать

Подписи к слайдам:

ЧЕТЫРЕХУГОЛЬНИК И ЕГО ЭЛЕМЕНТЫ

Рассмотрим фигуру, состоящую из четырех точек A , B , C , D A B C D и четырех отрезков AB, BC, CD, DA, таких, что никакие два соседних отрезка не лежат на одной прямой и никакие два несоседних отрезка не имеют общих точек Фигура, образованная этими отрезками, ограничивает часть плоскости. Эту часть плоскости называют ЧЕТЫРЕХУГОЛЬНИКОМ Вершины четырехугольника Стороны четырехугольника

Задание . Среди фигур, изображенных на рисунке, укажите четырехугольники.

Стороны четырехугольника, являющиеся соседними отрезками, называются соседними сторонами четырехугольника Вершины четырехугольника, являющиеся концами одной стороны, называют соседними вершинами четырехугольника Стороны четырехугольника, не являющиеся соседними, называют противолежащими сторонами четырехугольника Несоседние вершины четырехугольника, называют противолежащими вершинами четырехугольника Отрезок, соединяющий противолежащие вершины четырехугольника, называют диагональю четырехугольника

Задание . 1.Какие вершины четырехугольника являются соседними, противолежащими? 2.Какие стороны четырехугольника являются соседними, противолежащими?

Укажите: 1.вершины четырехугольника; Задание. Назовите четыре каких-нибудь обозначения четырехугольника. 2.стороны четырехугольника; 3.пары соседних вершин; 4.пары противолежащих вершин; 5.пары соседних сторон; 6.пары противолежащих сторон.

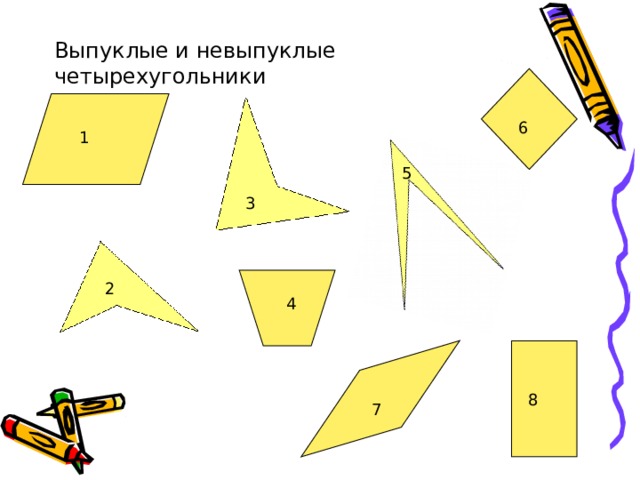
Углы ABC,BCD,CDA,DAB называют углами четырехугольника ABCD В этом четырехугольнике все они меньше развернутого угла. Такой четырехугольник называют выпуклым. В четырехугольнике ABCD ˪ ABC больше развернутого. Такой четырехугольник не является выпуклым.

Задание . Среди четырехугольников, изображенных на рисунке, назовите выпуклые.

Теорема . Сумма углов четырехугольника равна 360 º Дано : А BCD – четырехугольник Доказать : ˪А+˪В+˪С+˪ D =360 º Доказательство: Диагональ BD разбивает четырехугольник на два треугольника. Сумма углов треугольника равна 180°. Сумма углов четырехугольника ABCD равна сумме углов треугольников ABD и CBD. Значит, ˪А+˪В+˪С+˪ D =360 º Теорема доказана

Задание . Чему равен четвертый угол четырехугольника, если три его угла равны 78 º , 89 º и 93 º ? 100 º Задание . Найдите углы четырехугольника, если они равны между собой. 90 º

Следствие. В четырехугольнике только один из углов может быть больше развернутого Длина любой стороны четырехугольника меньше суммы длин трех остальных его сторон. Рассмотрим произвольный четырехугольник ABCD Проведем диагональ AC. Применяя неравенство треугольника для сторон AB и AC соответственно треугольников ABC и ADC , получаем неравенства: Решение. .

Задача. Может ли у четырехугольника быть: три прямых угла и один острый; три прямых угла и один тупой; четыре прямых угла; четыре острых угла; два прямых и два тупых угла; два прямых угла, один острый и один тупой? Задача. Могут ли стороны четырехугольника быть равными: 2 дм, 3 дм, 4 дм, 9 дм; 2 дм, 3 дм, 4 дм, 10 дм?

Видео:Четырехугольник | Геометрия 7-9 класс #41 | ИнфоурокСкачать

По теме: методические разработки, презентации и конспекты

Презентация «Мартинки-весенние куклы» (с элементами тестрования)

Занятие проводится с ребенком, имеющим ограниченные возможности здоровья и находящимся на надомной форме обучения. Проверка знаний ТБ при работе и итоги усвоения темы проводятся тестированием.

интерактивная презентация к уроку «Массовая доля элемента в молекуле»

Презентация в наглядной форме иллюстрирует способы нахождения массовой доли элемента в молекуле. Содержит динамические картинки, позволяющие лучше понять механизм вычисления массовой доли.

Презентация по химии по теме «Элементы таблицы Менделеева» (таблица и ученые)

Дополнительный материал для проведения уроков химии и внеурочной деятельности.

Своя-игра — презентация на темы — явление выстрела, элементы траектории, устройство автомата АК

презентация игра на темы — явление выстрела, элементы траектории, устройство автомата АК, построена по принципу популярной программы, проста в освоении и пригодится преподавателям, использующим и.

презентация к уроку «Общая характеристика элементов IIА группы»

9 класс. Общая характеристика элементов II А группы.

Презентация к уроку «Изложение с элементами сочинения «Троице-Сергиева лавра зимой».

Презентация к уроку «Изложение с элементами сочинения «Троице-Сергиева лавра зимой» представляет собой визуальный дидактический материал, в котором дана историческая справка о Лавре, словарная ра.

Презентация по математике «Куб». Рассмотрены элементы куба: грани, вершины, ребра и их количество, свойства.

Презентация может быть использована на уроке изучения нового материала и обобщения по теме «Куб». Расмотрены элементы куба: грани, вершины, ребра и их количества, свойства.

Видео:Четырехугольники. Вебинар | МатематикаСкачать

Презентация «Четырёхугольники»

Разработка может быть полезна как учителю математики при проведении уроков в 8 классе по теме «Четырёхугольники», так и учащимся при подготовке к экзамену по геометрию

Просмотр содержимого документа
«Презентация «Четырёхугольники»»

Фролова Ольга Александровна, учитель математики

МБОУ «Караваевская СОШ»

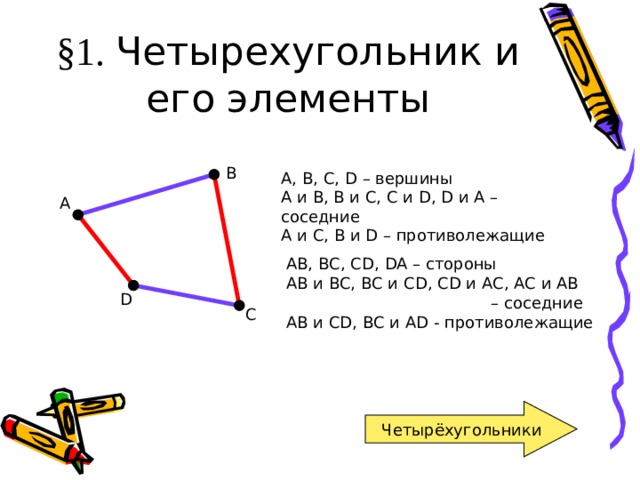
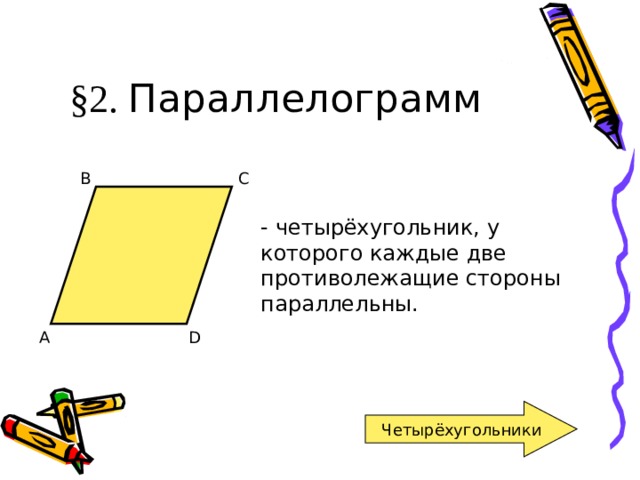
§ 1. Четырехугольник и его элементы

А, В, С, D – вершины

А и В, В и С, С и D , D и А – соседние

А и С, В и D – противолежащие

АВ, ВС, С D , DA – стороны

АВ и BC , ВС и CD , С D и АС, АС и АВ

АВ и С D , В C и AD — противолежащие

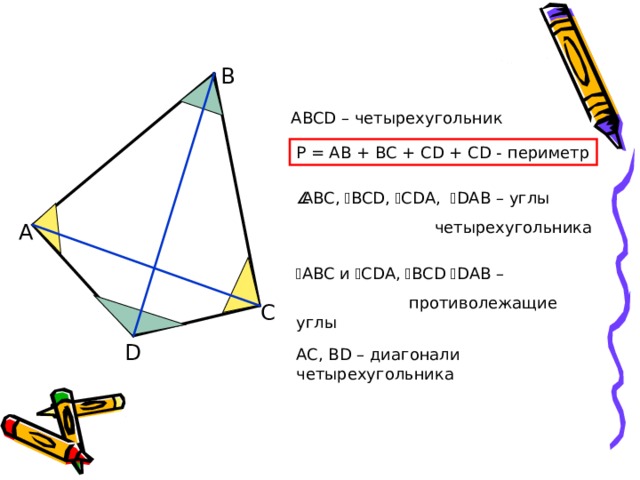
P = AB + BC + CD + CD — периметр

 ABC ,  BCD ,  CDA ,  DAB – углы

 ABC и  CDA ,  BCD  DAB –

AC , В D – диагонали четырехугольника

Выпуклые и невыпуклые четырехугольники

Сумма углов четырехугольника равна 360 º .

В четырехугольнике только один из углов может быть больше развёрнутого.

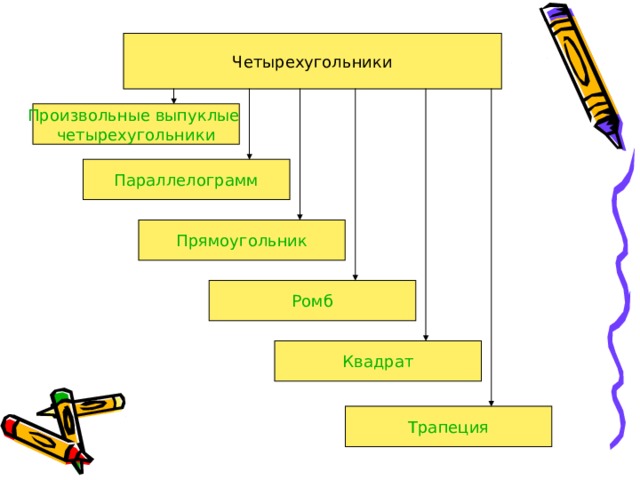
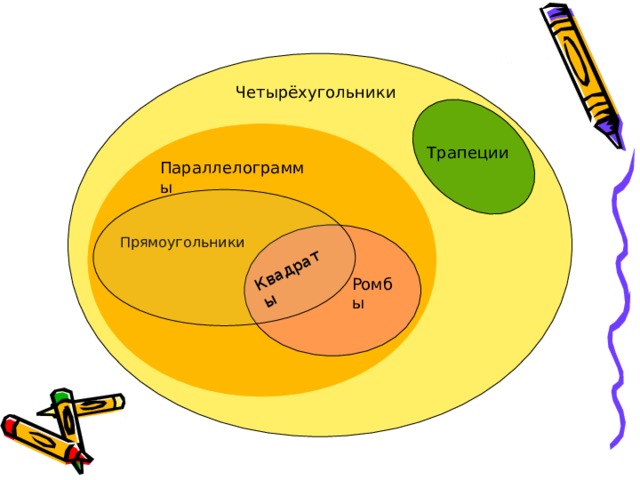
— четырёхугольник, у которого каждые две противолежащие стороны параллельны.

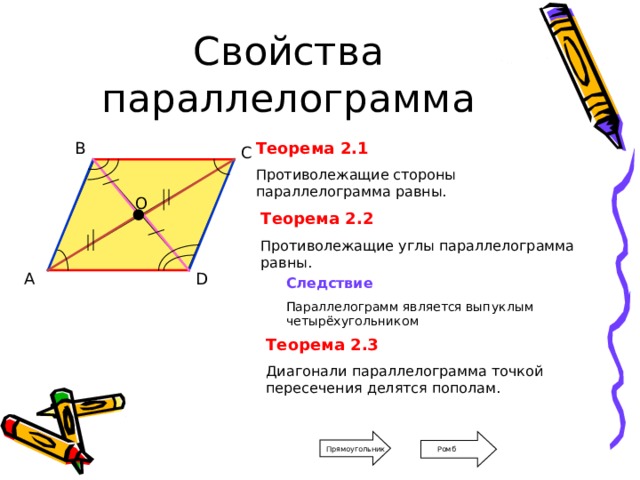
Противолежащие стороны параллелограмма равны.

Противолежащие углы параллелограмма равны.

Параллелограмм является выпуклым четырёхугольником

Диагонали параллелограмма точкой пересечения делятся пополам.

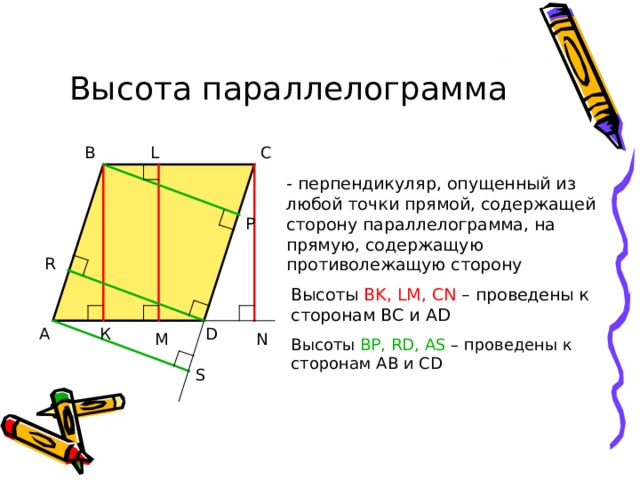
— перпендикуляр, опущенный из любой точки прямой, содержащей сторону параллелограмма, на прямую, содержащую противолежащую сторону

Высоты BK , LM , CN – проведены к сторонам ВС и AD

Высоты BP , RD , AS – проведены к сторонам A В и CD

§ 3. Признаки параллелограмма

Теорема 3.1 (обратная теореме 2.1)

Если в четырёхугольнике каждые две противолежащие стороны равны, то этот четырёхугольник – параллелограмм.

Если в четырёхугольнике две противолежащие стороны равны и параллельны, то этот четырёхугольник – параллелограмм.

Теорема 3.3 (обратная теореме 2.3)

Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.

Противолежащие стороны параллелограмма равны.

Если в четырёхугольнике каждые две противолежащие стороны равны , то этот четырёхугольник – параллелограмм.

Противолежащие углы параллелограмма равны.

Если в четырёхугольнике две противолежащие стороны равны и параллельны , то этот четырёхугольник – параллелограмм.

Диагонали параллелограмма точкой пересечения делятся пополам.

Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.

• Докажите, что длина любой стороны четырёхугольника меньше суммы длин трёх остальных его сторон.
• Докажите, что прямые, содержащие высоты треугольника, пересекаются в одной точке.
• Докажите, что сумма любых двух соседних углов параллелограмма равна 180 º (№43).
• Докажите, что угол между высотами параллелограмма, проведенными из вершины тупого угла, равен острому углу параллелограмма (№69).
• Докажите, что угол между высотами параллелограмма, проведенными из вершины острого угла, равен тупому углу параллелограмма (№70).
• Докажите, что если в четырёхугольнике каждые два противолежащих угла равны, то этот четырёхугольник – параллелограмм.
• Докажите, что если сумма углов, прилежащих к любой из двух соседних сторон четырёхугольника, равна 180 º , то этот четырехугольник – параллелограмм (№90).
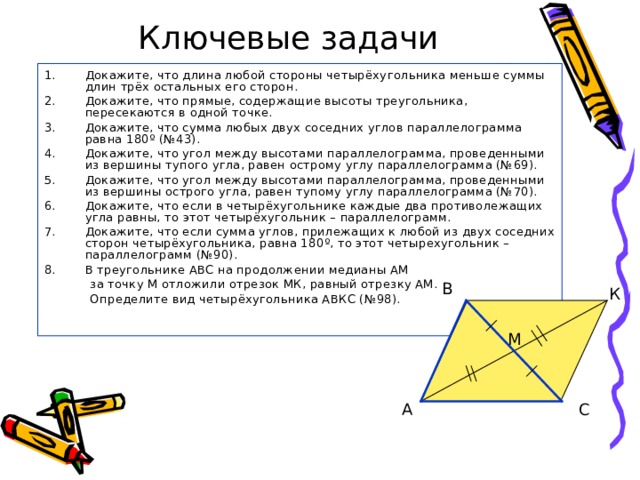
• В треугольнике АВС на продолжении медианы АМ

за точку М отложили отрезок МК, равный отрезку АМ.

Определите вид четырёхугольника АВКС (№98).

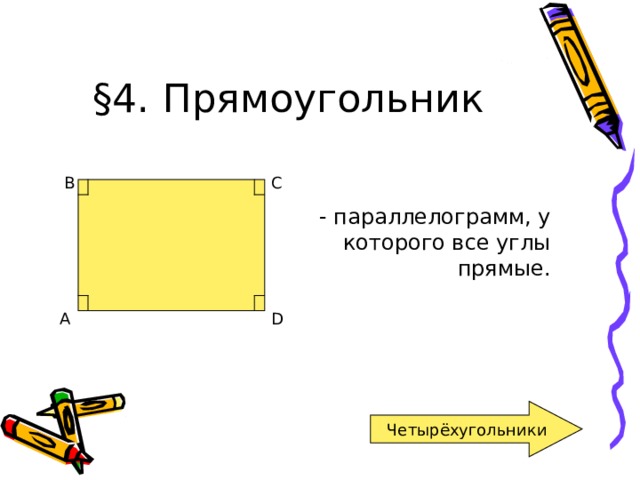
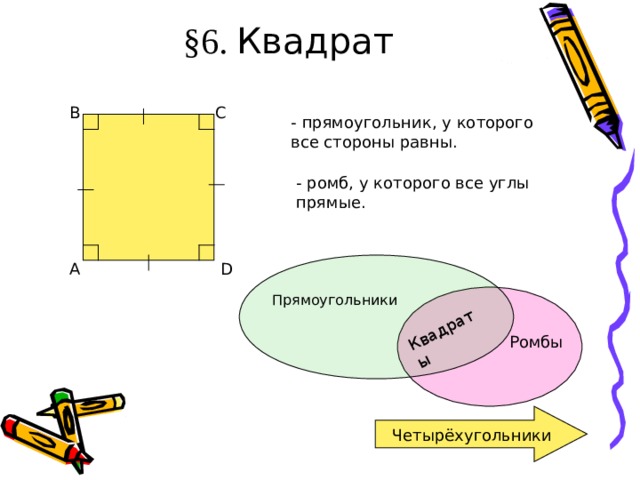
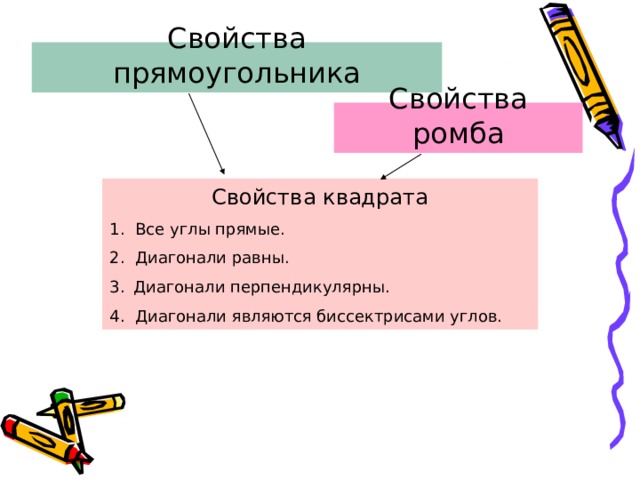
— параллелограмм, у которого все углы прямые.

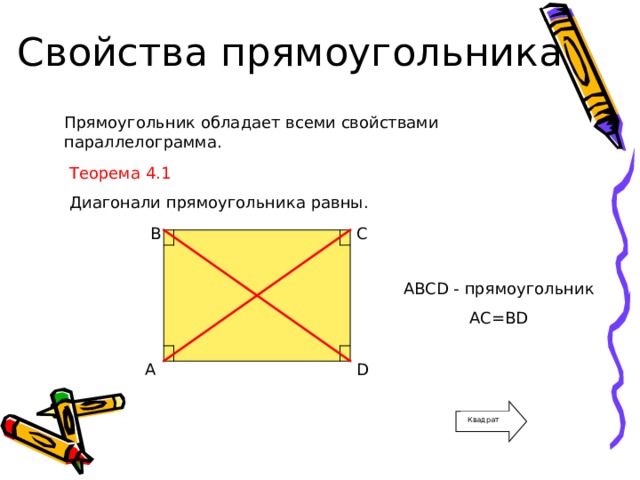
Прямоугольник обладает всеми свойствами параллелограмма.

Диагонали прямоугольника равны.

Если один из углов параллелограмма прямой, то этот паралеллограмм – прямоугольник .

Если диагонали параллелограмма равны, то этот паралеллограмм – прямоугольник .

1. Докажите, что четырёхугольник, все углы которого прямые, является прямоугольником (№122).

2. Докажите, что медиана прямоугольного треугольника, проведённая к гипотенузе, равна её половине (№124).

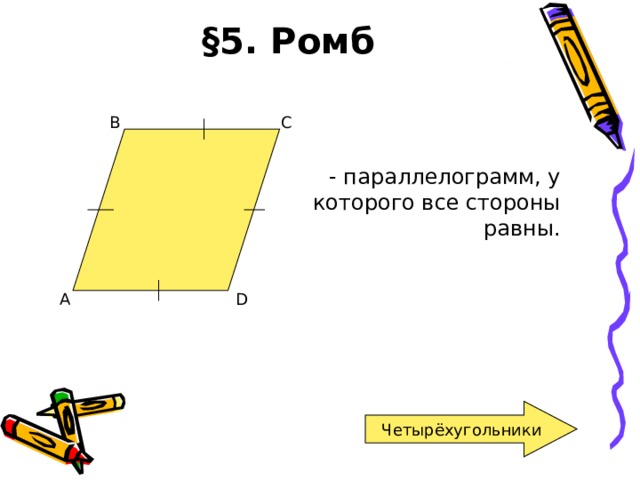
— параллелограмм, у которого все стороны равны.

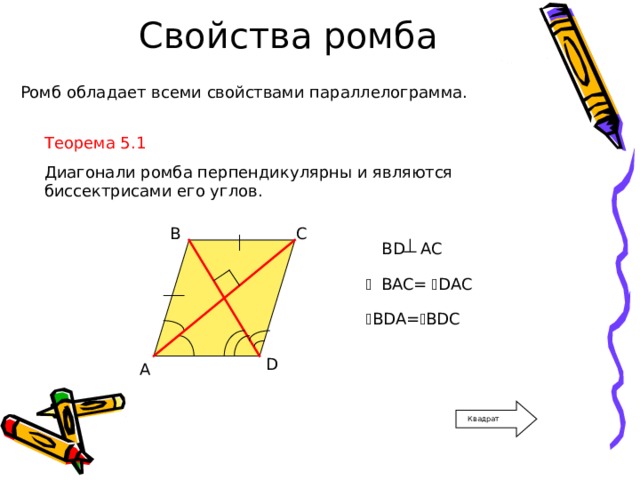
Ромб обладает всеми свойствами параллелограмма.

Диагонали ромба перпендикулярны и являются биссектрисами его углов.

Если диагонали параллелограмма перпендикулярны, то данный параллелограмм — ромб .

Если диагональ параллелограмма является биссектрисой его угла, то данный параллелограмм — ромб.

1. Докажите, что если две соседние стороны параллелограмма равны, то этот параллелограмм является ромбом (№137).

2. Докажите, что четырехугольник, у которого все стороны равны, является ромбом (№138).

3. Докажите, что высоты ромба равны (№148).

— прямоугольник, у которого все стороны равны.

— ромб, у которого все углы прямые.

1. Все углы прямые.

2. Диагонали равны.

4. Диагонали являются биссектрисами углов.

1. Докажите, что если один из углов ромба прямой, то этот ромб является квадратом (№165).

2. Докажите, что если две соседние стороны прямоугольника равны, то этот прямоугольник является квадратом (№166).

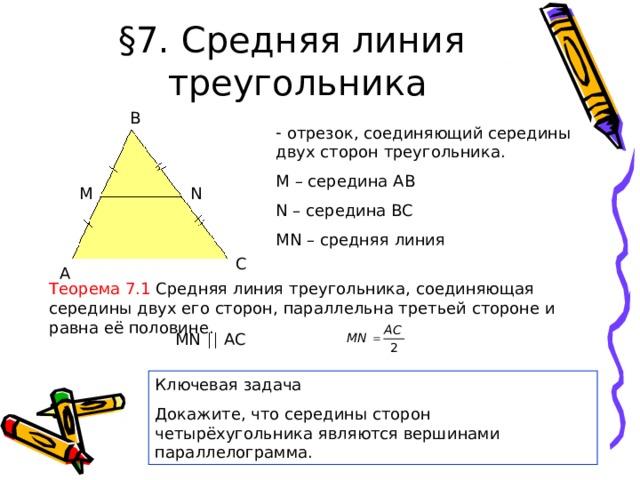
§ 7. Средняя линия

• отрезок, соединяющий середины двух сторон треугольника.

MN – средняя линия

Теорема 7.1 Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна её половине.

Докажите, что середины сторон четырёхугольника являются вершинами параллелограмма.

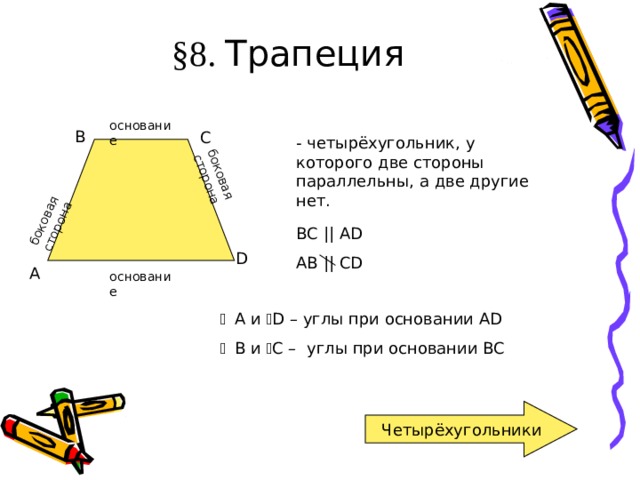
— четырёхугольник, у которого две стороны параллельны, а две другие нет.

 A и  D – углы при основании AD

 B и  C – углы при основании BC

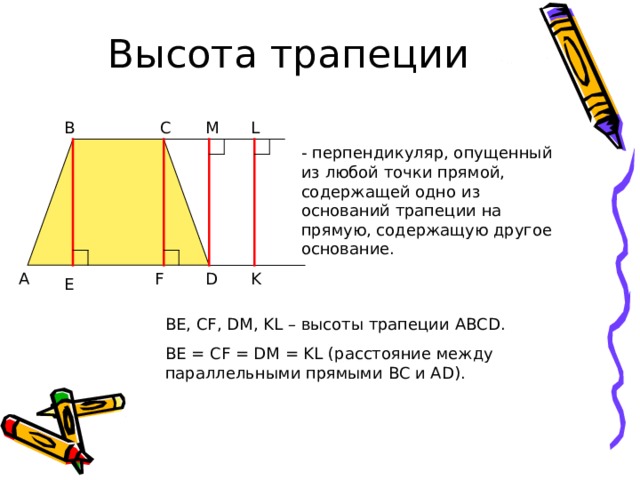
— перпендикуляр, опущенный из любой точки прямой, содержащей одно из оснований трапеции на прямую, содержащую другое основание.

BE, CF, DM, KL – высоты трапеции ABCD .

BE = CF = DM = KL ( расстояние между параллельными прямыми BC и AD) .

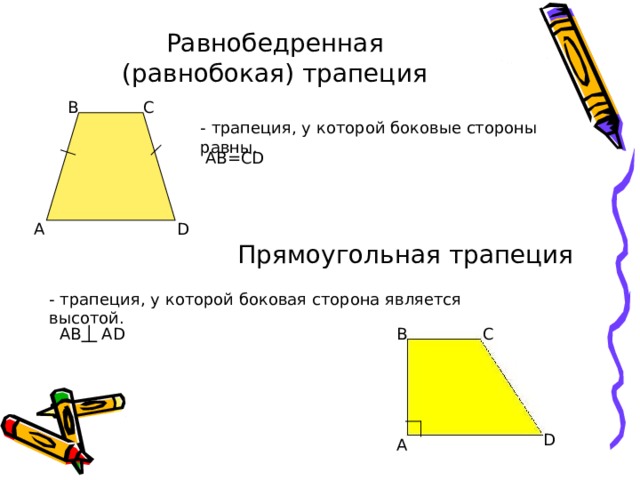
Равнобедренная (равнобокая) трапеция

— трапеция, у которой боковые стороны равны.

— трапеция, у которой боковая сторона является высотой.

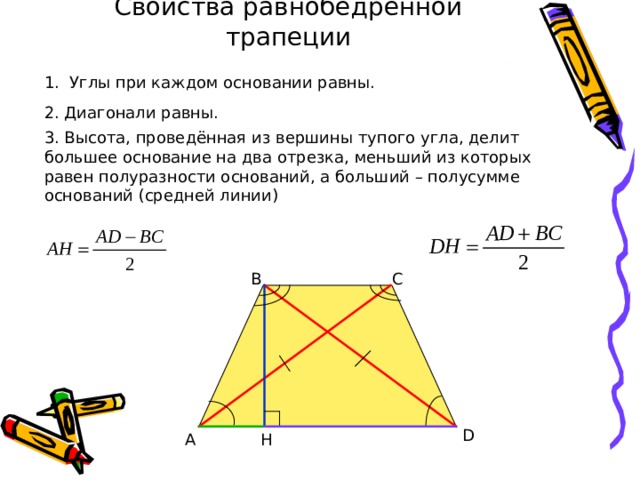
Свойства равнобедренной трапеции

1. Углы при каждом основании равны.

2. Диагонали равны.

3. Высота, проведённая из вершины тупого угла, делит большее основание на два отрезка, меньший из которых равен полуразности оснований, а больший – полусумме оснований (средней линии)

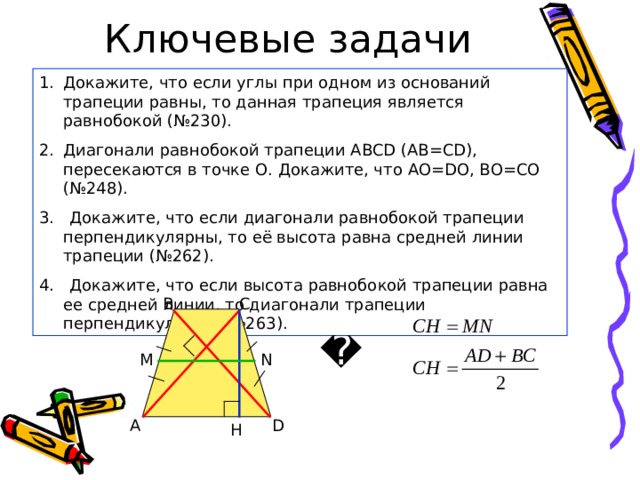
• Докажите, что если углы при одном из оснований трапеции равны, то данная трапеция является равнобокой (№230).

• Диагонали равнобокой трапеции ABCD ( AB=CD ), пересекаются в точке О. Докажите, что AO=DO, BO=CO ( №248) .

3. Докажите, что если диагонали равнобокой трапеции перпендикулярны, то её высота равна средней линии трапеции (№262).

4. Докажите, что если высота равнобокой трапеции равна ее средней линии, то диагонали трапеции перпендикулярны (№263).

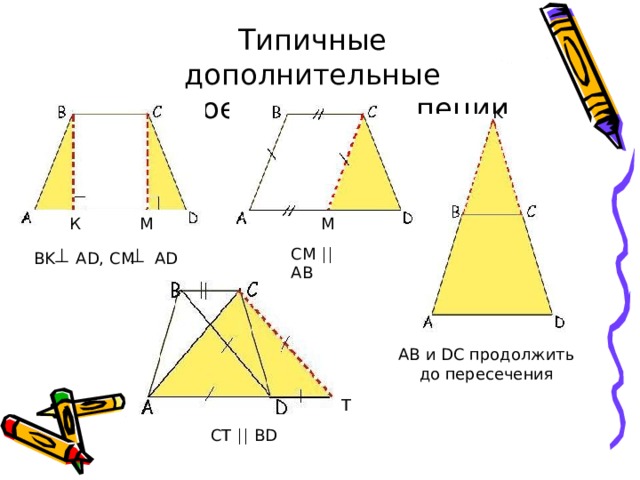
Типичные дополнительные построения для трапеции

AB и DC продолжить до пересечения

Список использованных источников

• Мерзляк А.Г. Геометрия : 8 класс : учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В. Б. Полонский, М.С. Якир. – М. : Вентана-Граф, 2018. – 208 с.

• Нелин Е. Геометрия. 7-11 классы. Определения, свойства,

методы решения задач — в таблицах. / Е. П. Нелин. — 2-е

изд., испр. — Москва : Илекса, 2019. — 80 с.

🌟 Видео

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Миникурс по геометрии. ЧетырехугольникиСкачать

Виды четырёхугольниковСкачать

Математика 5 класс (Урок№29 - Четырёхугольники.)Скачать

Четырехугольники. Геометрия 8 класс.Скачать

ГЕОМЕТРИЯ 8 класс: Четырехугольники | Видеоурок с теорией и решением задачиСкачать

МЕРЗЛЯК-8. ГЕОМЕТРИЯ. ЧЕТЫРЕХУГОЛЬНИК. ПАРАГРАФ-1. ТЕОРИЯСкачать

3 правила для вписанного четырехугольника #shortsСкачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Четырёхугольник и его элементы Геометрия 8клСкачать

Геометрия 8 класс (Урок№1 - Многоугольники. Четырёхугольник.)Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Вписанные четырехугольники. 9 класс.Скачать