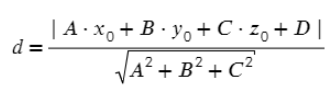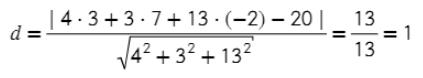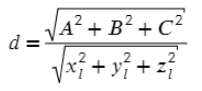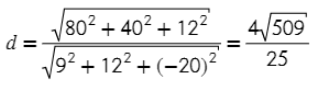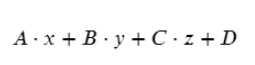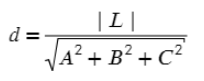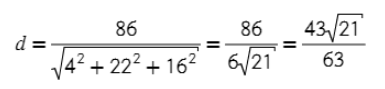Расстояние между вектором и плоскостью

• +7 (953) 35-222-89
• Санкт-Петербург, Лиговский пр.52
• Kyziaha@gmail.com

Метод координат (расстояние между точкой и плоскостью, между прямыми)

Расстояние между точкой и плоскостью.

Расстояние между точкой и прямой.

Расстояние между двумя прямыми.

Первое, что полезно знать, это как найти расстояние от точки до плоскости:

Значения A, B, C, D — коэффициенты плоскости

x, y, z — координаты точки

Задача. Найти расстояние между точкой А = (3; 7; −2) и плоскостью 4x + 3y + 13z — 20 = 0.

Все дано, можно сразу подставить значения в уравнение:

Задача. Найдите расстояние от точки К = (1; −2; 7) до прямой, проходящей через точки V = (8; 6; −13) и T = (−1; −6; 7).

1. Находим вектор прямой.
2. Вычисляем вектор, проходящий через искомую точку и любую точку на прямой.
3. Задаем матрицу и находим определитель по двум полученным векторам в 1-ом и 2-ом пункте.
4. Расстояние получим, когда квадратный корень из суммы квадратов коэффициентов матрицы поделим на длину вектора, который задает прямую (Думаю непонятно, поэтому перейдем к конкретному примеру).

1) TV = (8−(−1); 6−(−6); -13-7) = (9; 12; −20)

2) Вектор найдем через точки K и T, хотя так же можно было бы через K и V или любую другую точку на данной прямой.

TK = (1−(−1); −2−(−6); 7-7) = (2; 4; 0)

3) П олучится м атрица без коэффициента D (здесь он не нужен для решения):

Если непонятно, как получить матрицу и ее определитель, смотрите здесь более подробный разбор.

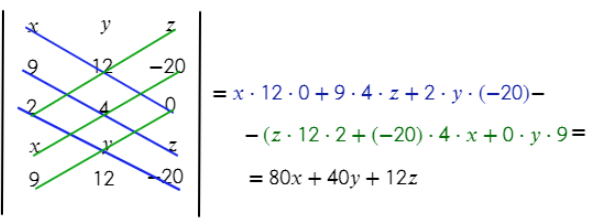
4) Плоскость получилась с коэффициентами А = 80, В = 40, С = 12,

x, y, z — координаты вектора прямой, в данном случае — вектор TV имеет координаты (9; 12; −20)

Задача. Найти расстояние между прямой, проходящей через точки Е = (1; 0; −2), G = (2; 2; −1), и прямой, проходящей через точки M = (4; −1; 4), L = (−2; 3; 0).

1. Задаем векторы обеих прямых.
2. Находим вектор, взяв по одной точке с каждой прямой.
3. Записываем матрицу из 3-х векторов (две строчки из 1-го пункта, одна строчка из 2-го) и находим ее численный определитель.
4. Задаем матрицу из двух первых векторов (в пункте 1). Первую строчку задаем как x, y, z.
5. Расстояние получим, когда разделим получившееся значение из пункта 3 по модулю на квадратный корень из суммы квадратов пункта 4.

Перейдем к цифрам:

1) EG = (2−1; 2−0; −1−2) = (1; 2; −3)

ML = (−2−4; 3−(−1); 0−4) = (−6; 4; −4)

2) Найдем вектор EM (можно было так же найти EL или GM, или GL).

EM = (1−4; 0−(−1); −2−4) = (−3; 1; −6)

3) Составляем матрицу из трех выше найденных векторов и находим определитель.

4) Составляем матрицу из первых двух выше найденных векторов и находим определитель

без коэффициента D (здесь он не нужен для решения).

Вспомним, что уравнение плоскости задается так:

В нашем случае А = 4, В = 22, С = 16, D = 0.

5) Итоговая формула выглядит так, где L= −86 (из 3 пункта)

Видео:7. Расстояние от точки до плоскости (вывод формулы примеры)Скачать

Векторы. Метод координат. Угол между прямыми, плоскостями. Расстояние от точки до плоскости, между скрещивающимися прямыми

(<color<textbf>>)
(bullet) Если в пространстве заданы две точки (A(x_1;y_1;z_1)) и (B(x_2;y_2;z_2)) , то вектор (overrightarrow) имеет координаты [overrightarrow = ]
(bullet) Если в пространстве заданы два вектора (vec =) и (vec= ) , то:

(qquad blacktriangleright) разность этих векторов (vec-vec=)

(bullet) Справедливы следующие утверждения:

I. Скалярное произведение ненулевых векторов (их длины не равны нулю) равно нулю тогда и только тогда, когда они перпендикулярны: [(vec, vec)=0 quadLeftrightarrowquad vecperp vec]

II. Длина вектора равна квадратному корню из скалярного произведения вектора на себя: [|vec|=sqrt]

III. Переместительный закон: [(vec, vec)=(vec, vec)]

(<color<textbf>>)
(bullet) Если (vec=) – нормаль к плоскости, то уравнение плоскости имеет вид [ax+by+cz+d=0] Для того, чтобы найти (d) , нужно подставить в уравнение плоскости вместо (x, y, z) координаты любой точки, лежащей в этой плоскости. Пример: если (vec=) – нормаль к плоскости, (O(4;5;6)) – точка из плоскости, то справедливо: (1cdot 4+2cdot 5+3cdot 6+d=0) , откуда (d=-32) , следовательно, уравнение плоскости имеет вид (x+2y+3z-32=0) . (bullet) Уравнение плоскости можно составить, используя три точки из плоскости, не лежащие на одной прямой.
Пусть (A(1;0;0), B(0;3;4), C(2;0;5)) – точки из плоскости. Тогда уравнение плоскости можно найти, решив систему: [begin 1cdot a+0cdot b+0cdot c+d=0\ 0cdot a+3cdot b+4cdot c+d=0\ 2cdot a+0cdot b+5cdot c+d=0end quadRightarrowquad begin d=-a\ 3b+4c-a=0\ a+5c=0endquadRightarrowquad begin d=-a\ a=-5c\ b=-3cendquadRightarrowquadbegina=-5c\ b=-3c\ d=5cend] Следовательно, уравнение плоскости имеет вид: [-5ccdot x-3ccdot y+ccdot z+5c=0] Можно разделить обе части на (c) , так как (cne 0) (иначе (a=b=c=d=0) ), следовательно, уравнение плоскости имеет вид [-5x-3y+z+5=0]

(<color<textbf>>)
(bullet) Если (M(x_0;y_0;z_0)) — некоторая точка вне плоскости (phi) , (ax+by+cz+d=0) — уравнение плоскости (phi) , то расстояние от точки (M) до плоскости (phi) ищется по формуле: [rho(M, phi)=dfrac<sqrt>]
(bullet) Для того, чтобы найти расстояние между скрещивающимися прямыми, нужно
— построить плоскость, проходящую через одну из них и параллельную другой;
— найти уравнение этой плоскости;
— найти расстояние от любой точки первой прямой до этой плоскости.

Видео:10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Видео:21. Угол между прямой и плоскостьюСкачать

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Видео:Определение кратчайшей расстоянии от точки до плоскостиСкачать

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

🎥 Видео

10 класс, 21 урок, Угол между прямой и плоскостьюСкачать

Угол между прямой и плоскостью. Видеоурок по геометрии 10 классСкачать

Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

Перпендикуляр и наклонная в пространстве. 10 класс.Скачать

Урок 3. Как найти угол между прямой и плоскостью || Задание №13. Стереометрия на ЕГЭСкачать

Расстояние от точки до плоскости. 11 класс.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Видеоурок "Расстояние между прямыми в пространстве"Скачать

Расстояние между параллельными плоскостямиСкачать

Метод координат для ЕГЭ с нуля за 30 минут.Скачать

Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей | Математика | TutorOnlineСкачать

11 класс, 7 урок, Вычисление углов между прямыми и плоскостямиСкачать

Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

9. Угол между плоскостями Условия параллельности и перпендикулярности плоскостейСкачать