Запишите уравнения прямой проходящей через точку м 2 3 параллельно оси ординат

Математика | 5 — 9 классы

Напишите уравнение прямой, проходящей через точку M(3 ; —2) и параллельной оси ординат.

Уравнение такой прямой, параллельной оси ординат можно записать х = а,

где а — абцисса точки пересечения прямой и оси ОХ

У нас прямая проходит через точку М(3 ; — 2), то есть абцисса равна 3, следовательно уравнение можно записать :

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Написать уравнение прямой параллельной оси 0y, проходящей через точку B(3 ; — 1)?

Написать уравнение прямой параллельной оси 0y, проходящей через точку B(3 ; — 1).

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Через точку А ( — 4 ; 2) проведена прямая, параллельная оси ординат?

Через точку А ( — 4 ; 2) проведена прямая, параллельная оси ординат.

Укажите координаты точки пересечения этой прямой с осью абсцисс.

Видео:Уравнение прямой, проходящей через точку параллельно OX, OY или через начало координат. Урок 5. 8 клСкачать

Напишите уровнение прямой проходящей через точку А(4 ; — 5) и параллельной оси ордината?

Напишите уровнение прямой проходящей через точку А(4 ; — 5) и параллельной оси ордината.

Видео:12. Уравнения прямой в пространстве Решение задачСкачать

Через точку А( — 2 ; 3) проведена прямая, параллельная оси ординат?

Через точку А( — 2 ; 3) проведена прямая, параллельная оси ординат.

Какая из точек лежит на этой прямой?

Видео:№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать

Составьте уравнение прямой, проходящий через точку пересечения графиков линейной функции y = 9x — 28 и y = 13x + 12 параллельно : а) оси абсцисс б) оси ординат?

Составьте уравнение прямой, проходящий через точку пересечения графиков линейной функции y = 9x — 28 и y = 13x + 12 параллельно : а) оси абсцисс б) оси ординат.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Составьте уравнения двух прямых, проходящих через точку A(4 ; 5) так, чтобы одна прямая была параллельна оси Ox, а вторая — оси Oy?

Составьте уравнения двух прямых, проходящих через точку A(4 ; 5) так, чтобы одна прямая была параллельна оси Ox, а вторая — оси Oy.

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Составить уравнение прямой у = ах + в Проходящей через точки А(1 ; 2) и В( — 1 ; — 12)?

Составить уравнение прямой у = ах + в Проходящей через точки А(1 ; 2) и В( — 1 ; — 12).

Найти координаты точки пересечения этой прямой с осью ординат.

Видео:№977. Напишите уравнения прямых, проходящих через точку М (2; 5) и параллельных осям координат.Скачать

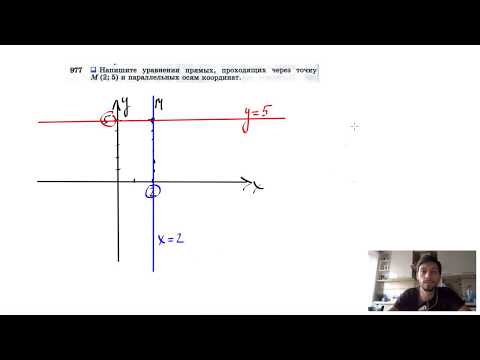
Составить уравнение прямой проходящей через точки ( — 5 ; — 2) и отсекающей оси ординат отрезок в = — 12?

Составить уравнение прямой проходящей через точки ( — 5 ; — 2) и отсекающей оси ординат отрезок в = — 12.

Видео:Видеоурок "Уравнение прямой, проходящей через две точки"Скачать

Напишите уравнение прямой, проходящей через точку А(2 ; 3) и параллельную прямой, заданной уравнением у = х?

Напишите уравнение прямой, проходящей через точку А(2 ; 3) и параллельную прямой, заданной уравнением у = х.

Видео:Видеоурок "Канонические уравнения прямой"Скачать

Найти уравнение прямой, отсекающей на оси ординат отрезок, равный 2, и проходящей параллельно прямой 2у–х = 3?

Найти уравнение прямой, отсекающей на оси ординат отрезок, равный 2, и проходящей параллельно прямой 2у–х = 3.

Перед вами страница с вопросом Напишите уравнение прямой, проходящей через точку M(3 ; —2) и параллельной оси ординат?, который относится к категории Математика. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

(16 + b) + 4 = 16 + 4 + b = 20 + b (b + 22) + 18 = 22 + 18 + b = 40 + b (43 + y) + 57 = 57 + 43 + y = 100 + y.

1) 18 * 100 / 12 = 150 м 75 * 100 / 12 = 625 м 3) 12 * 100 / 15 = 80 см 2, 7 / 100 / 15 = 18 см 5) 21 * 100 / 35 = 60 км 11, 2 * 100 / 35 = 32 км.

A = mq + r, где q и r(остаток) целые числа и 0≤r.

40 : 6 = 6 ( ост. 4) 65 : 8 = 8 (ост. 1) 76 : 10 = 7 (ост. 6) 33 : 2 = 14 (ост. 5).

Кувшин — 2 1 / 4 Бутылка — ? На 1, 5 меньше чем в кувшине Бидон — ? В 1 / 3 больше чем в кувшине 2 1 / 4 можем превратить в десятичную (по желанию так легче) = 2, 25 1)2, 25 — 1, 5 = 0, 75 литров или же 75 / 100 2)2 1 / 4 : 1 / 3 = 6 3 / 4 3) 2 1 /..

Максимальное трехзначное число 999, поэтому 999 + 998 + 997 = 2994 .

— 2, 1x + 6. 3 — 90. 8 = 0 — 2. 1x — 84. 5 = 0 — 2. 1x — 84. 5 x = — 845 / 21 или x = — 405 / 21.

14 — 2 = 12лет разница х — это возраст Вани , когда он будет старше Вовы в 3 раза х : 3 = (14 — 12) * 3 3х = (14 — 12) * 3 * 3 Х = 18 18лет будет Ване 18 : 3 = 6лет Вове 18 — 6 = 12лет разница.

15 + 15 = 30 30 : 6 = 5(Делится, значит не подходит) 30 + 15 = 45(45 на 6 не делится).

45 потому что 45 делится на 15, но не делится на 6.

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Самостоятельная работа по геометрии на тему: «Уравнение прямой» (9 класс)

Видео:9 класс, 7 урок, Уравнение прямойСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Геометрия 9 класс

Видео:Уравнение параллельной прямойСкачать

Самостоятельная работа по теме:

Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -1) и В (-4; -3) на прямой 2х – у + 5 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (2; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-2; -1) и В (3; 1).

Видео:Составляем уравнение прямой по точкамСкачать

Геометрия 9 класс

Видео:2. Уравнение плоскости примеры решения задач #1Скачать

Самостоятельная работа по теме:

1. Проверить, лежат ли точки А (-5; 3) и В (9; 4) на прямой х – 4у + 7 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-5; 3), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (-3; -3) и В (3; 5).

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Геометрия 9 класс

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Самостоятельная работа по теме:

Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

«Уравнение прямой»

1. Проверить, лежат ли точки А (-2; 5) и В (3; -1) на прямой 3х – у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (6; -2), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-2; 3) и В (4; -1).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (7; -2) и В (-5; 4) на прямой х + 2у – 3 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-4; 3), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (1; 4) и В (-5; 2).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -1) и В (-4; -3) на прямой 4х – у + 13 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (4; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-3; -1) и В (4; 1).

Геометрия 9 класс

Самостоятельная работа по теме:

1. Проверить, лежат ли точки А (-5; 3) и В (10; 4) на прямой х – 3у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-4; 2), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (-2; -3) и В (3; 4).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (-4; 5) и В (4; -2) на прямой 3х – у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (4; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-3; 3) и В (8; -1).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -2) и В (-4; 4) на прямой х + 2у – 3 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-3; 4), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (2; 4) и В (-3; 2).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -1) и В (-4; -3) на прямой 2х – у + 5 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (2; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-2; -1) и В (3; 1).

Геометрия 9 класс

Самостоятельная работа по теме:

1. Проверить, лежат ли точки А (-5; 3) и В (9; 4) на прямой х – 4у + 7 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-5; 3), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (-3; -3) и В (3; 5).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (-2; 5) и В (3; -1) на прямой 3х – у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (6; -2), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-2; 3) и В (4; -1).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (7; -2) и В (-5; 4) на прямой х + 2у – 3 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-4; 3), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (1; 4) и В (-5; 2).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -1) и В (-4; -3) на прямой 4х – у + 13 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (4; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-3; -1) и В (4; 1).

Геометрия 9 класс

Самостоятельная работа по теме:

1. Проверить, лежат ли точки А (-5; 3) и В (10; 4) на прямой х – 3у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-4; 2), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (-2; -3) и В (3; 4).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (-4; 5) и В (4; -2) на прямой 3х – у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (4; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-3; 3) и В (8; -1).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -2) и В (-4; 4) на прямой х + 2у – 3 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-3; 4), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (2; 4) и В (-3; 2).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -1) и В (-4; -3) на прямой 2х – у + 5 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (2; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-2; -1) и В (3; 1).

Геометрия 9 класс

Самостоятельная работа по теме:

1. Проверить, лежат ли точки А (-5; 3) и В (9; 4) на прямой х – 4у + 7 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-5; 3), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (-3; -3) и В (3; 5).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (-2; 5) и В (3; -1) на прямой 3х – у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (6; -2), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-2; 3) и В (4; -1).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (7; -2) и В (-5; 4) на прямой х + 2у – 3 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-4; 3), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (1; 4) и В (-5; 2).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -1) и В (-4; -3) на прямой 4х – у + 13 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (4; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-3; -1) и В (4; 1).

Геометрия 9 класс

Самостоятельная работа по теме:

1. Проверить, лежат ли точки А (-5; 3) и В (10; 4) на прямой х – 3у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-4; 2), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (-2; -3) и В (3; 4).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (-4; 5) и В (4; -2) на прямой 3х – у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (4; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-3; 3) и В (8; -1).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -2) и В (-4; 4) на прямой х + 2у – 3 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-3; 4), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (2; 4) и В (-3; 2).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -1) и В (-4; -3) на прямой 2х – у + 5 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (2; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-2; -1) и В (3; 1).

Геометрия 9 класс

Самостоятельная работа по теме:

1. Проверить, лежат ли точки А (-5; 3) и В (9; 4) на прямой х – 4у + 7 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-5; 3), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (-3; -3) и В (3; 5).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (-2; 5) и В (3; -1) на прямой 3х – у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (6; -2), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-2; 3) и В (4; -1).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (7; -2) и В (-5; 4) на прямой х + 2у – 3 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-4; 3), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (1; 4) и В (-5; 2).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -1) и В (-4; -3) на прямой 4х – у + 13 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (4; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-3; -1) и В (4; 1).

Геометрия 9 класс

Самостоятельная работа по теме:

1. Проверить, лежат ли точки А (-5; 3) и В (10; 4) на прямой х – 3у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-4; 2), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (-2; -3) и В (3; 4).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (-4; 5) и В (4; -2) на прямой 3х – у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (4; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-3; 3) и В (8; -1).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -2) и В (-4; 4) на прямой х + 2у – 3 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-3; 4), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (2; 4) и В (-3; 2).

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 966 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 342 человека из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 688 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Самостоятельная работа по геометрии «Некоторые свойства окружности. Касательная к окружности» (7 класс)

Урок по теме: «Площади фигур»

Урок по теме: «Площади подобных фигур»

Конспект урока по теме: «Свойства равнобедренного треугольника» (Геометрия, 7 класс)

Самоятоятельная работа «Расстояние между точками. Длина вектора» (9 класс)

Самостоятельная работа «Умножение вектора на число» (9 класс)

Презентация. Площадь многоугольника. Устный счет

Презентация. Прямоугольник, ромб, квадрат

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5442018 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Правительство направит регионам почти 92 миллиарда рублей на ремонт и оснащение школ

Время чтения: 1 минута

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Россия направит $10,3 млн на развитие школьного питания в нескольких странах

Время чтения: 1 минута

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Прямые на координатной плоскости

Линейная функция

График линейной функции

Прямые, параллельные оси ординат

Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые

Линейная функция

Линейной функцией называют функцию, заданную формулой

где k и b – произвольные (вещественные) числа.

При любых значениях k и b графиком линейной функции является прямая линия .

Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .

График линейной функции

При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.

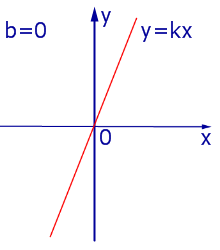Рис.1

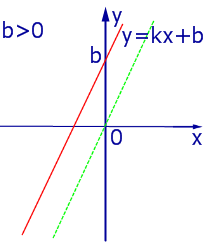Рис.2

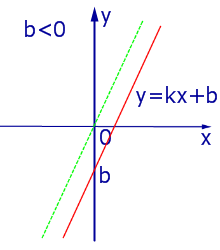Рис.3

При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.

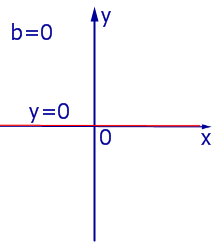Рис.4

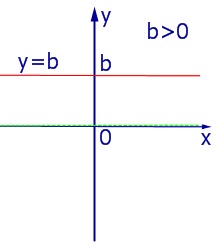Рис.5

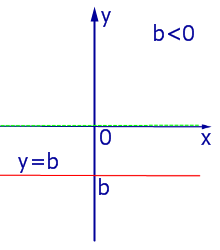Рис.6

При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.

k y = kx + b1 и y = kx + b2 , имеющие одинаковые угловые коэффициенты и разные свободные члены , параллельны . имеющие разные угловые коэффициенты , пересекаются при любых значениях свободных членов. y = kx + b1 и перпендикулярны при любых значениях свободных членов. Угловой коэффициент прямой линии y = kx (2) равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2). Рис.10 Рис.11 Рис.12 Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b . При прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле Прямые, параллельные оси ординат Прямые, параллельные оси Oy , задаются формулой x = c , (3) где c – произвольное число, и изображены на рис. 13, 14, 15. Рис.13 Рис.14 Рис.15 Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .; Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые px + qy = r , (4) где p, q, r – произвольные числа. В случае, когда уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию . что и требовалось. В случае, когда получаем: откуда вытекает, что уравнение (4) задает прямую линию вида (3). В случае, когда q = 0, p = 0, уравнение (4) имеет вид 0 = r , (5) и при r = 0 его решением являются точки всей плоскости: В случае, когда уравнение (5) решений вообще не имеет. Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением px + qy = r1 , (6) параллельна прямой, заданной уравнением (4) . Замечание 3 . При любом значении r2 прямая линия, заданная уравнением – qx + py = r2 , (7) перпендикулярна прямой, заданной уравнением (4) . Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и параллельной к прямой 4x + 5y = 7 ; (8) перпендикулярной к прямой (8). В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде 4x + 5y = r1 , (9) где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство Итак, уравнение прямой, параллельной к прямой В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде – 5x + 4y = r2 , (10) где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство Поделиться или сохранить к себе: Смотрите также 2 параллельные прямые пересекает 3 прямая a параллельна bc пересекает a и b и не 2 параллельные прямые пересекаются 3 прямой найди углы сумма которых данным углом равна 180 градусов 2 параллельные прямые пересечены 3 прямой то внутренние накрест лежащие углы равны 2 прямые параллельны одной и той же плоскости можно ли утверждать что эти прямые Четырехугольник у которого противолежащие стороны параллельны то есть лежат на параллельных прямых 1 вписанный угол опирающийся на полуокружность острый 2 если две параллельные прямые пересечены 1 даны 2 параллельные прямые и секущая построить окружность касающуюся всех 3 х прямых 1 из внутренних односторонних углов образованных при пересечении 2 параллельных прямых 3 прямой